미타그-레플러 함수

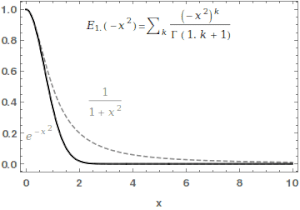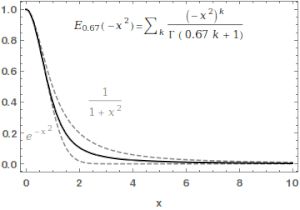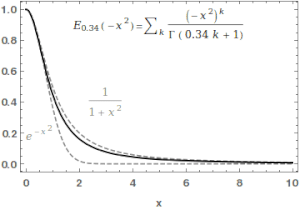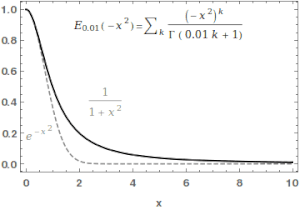
수학에서 미타그-레플러 함수_α,β E는 특수한 함수로서, 복잡한 함수로서 두 개의 복잡한 매개변수 α와 β에 의존한다.α의 실제 부분이 엄격히 양의 값일 때 다음과 같은 시리즈로 정의할 수 있다.^[1][2]

${\displaystyle E_{\alpha ,\beta }(z)=\sum _{k=0}^{\inflt }{\frac {z^{k}}{\Alpha k+\beta )},},},}$

여기서 $\gamma {\displaystyle \mathrm{}}$( ${\displaystyle x}$) ${\displaystyle \Gamma (x)}$은 감마함수다.$\beta {\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle \beta =1}$일$$때 $E{\displaystyle {}_{}}$ ${\displaystyle {\alpha }_{}}$ ${\displaystyle z}$)${\displaystyle }$= ${\displaystyle {\mathrm{E}}_{}}$ ${\displaystyle {\alpha }_{}}$, 1${\displaystyle {}_{}}$( ${\displaystyle z}$) ${\displaystyle E_{\alpha }(z)=$로 약칭된다.$E_{\alpha ,1}(z)}$. For ${\displaystyle \alpha =0}$, the series above equals the Taylor expansion of the geometric series and consequently ${\displaystyle E_{0,\beta }(z)={\frac {1}{\Gamma (\beta )}}{\frac {1}{1-z}}}$.

α와 β가 진짜이고 양인 경우, 시리즈는 인수 z의 모든 값에 대해 수렴되므로 미타그-레플러 함수는 전체 함수다.이 기능은 괴스타 미타그-레플러의 이름을 따서 명명되었다.이 종류의 기능은 분수 미적분학 이론에서 중요하다.

α > 0의 경우, 미탁-레플러 $함수{\displaystyle {}_{}}$ E${\displaystyle {\alpha }_{}}$ , ${\displaystyle 1{}_{}}$(${\displaystyle }$z ) ${\displaystyle E_{\alpha ,1}(z)}$는 순서 1/α의 전체 함수로서$$, 어떤 의미에서는 순서의 전체 함수 중 가장 단순하다.

미탁-레플러 함수는 재발 특성을 만족한다(Theorem 5.1 of )

${\displaystyle E_{\alpha ,\beta }(z)={\frac {1}{z}E_{\alpha,\beta -\alpha }-{\frac {1}{z\beta -\alpha,}}}}}$

거기서 푸앵카레 점증식 팽창이 일어났다.

${\displaystyle E_{\alpha ,\beta }\sim -\sum _{k=1}{\frac {1}{z^{k}\감마(\beta -k\alpha )}}}}}$

$다음{\displaystyle }$ 중 z${\displaystyle }$→ -${\displaystyle \mathrm{\infty }}$ ${\displaystyle z\to$ -$\fty }$에 해당된다$.$

특례

$\alpha {\displaystyle }$= ${\displaystyle 0,}$ ${\displaystyle 1}$,${\displaystyle 1}$, ${\displaystyle 2\mathrm{}}$,${\displaystyle 2}$ ${\displaystyle \alpha =0,1/2,1,2}$의 경우, (의 2절)을$$ 참조하십시오.

오류 함수:

${\displaystyle E_{\frac {1}{1}{1}:{2}}(z)=\exp(z^{2})\operatorname {erfc}(-z).}$

기하학적 진행의 합계:

${\displaystyle E_{0}(z)=\sum _{k=0}^{\npty }z^{k}={\frac {1}{1-z},\, z <1>.}$

지수 함수:

${\displaystyle E_{1}(z)=\sum _{k=0}^{\inflat }{\frac {z^{k}}{\frac {n1}}}{\frac {z^{k}}}{k!}}}=\exp(z).}$

쌍곡선 코사인:

${\displaystyle E_{2}(z)=\cosh({\sqrt{z}),{\text{ 및 }E_{2}(-z^{2})=\cos(z).}$

$\beta {\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle \beta =$2}의$$경우$,$

${\displaystyle E_{1,2}(z)={\frac {e^{z}-1}{z},}$

${\displaystyle E_{2,2}(z)={\frac {\sinh({\sqrt {z})}{\sqrt {z}}.}$

$\alpha {\displaystyle }$= ${\displaystyle 0,}$ ${\displaystyle 1}$, ${\displaystyle 2}$ ${\displaystyle \alpha =0,1,2}$의 경우$$적분

${\daystyle \int _{0}^{z}E_{\alpha }(-s^{2})\,{\mathrm {d}s}$

각각 제공: ${\displaystyle \arctan }$ ${\displaystyle }$( ${\displaystyle z}$) ${\$$displaystyle \arctan($$z)},$$\pi {\displaystyle \frac{\sqrt{}}{}}$ ${\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \mathrm{erf}}$ ${\displaystyle }$(${\displaystyle z}$) ${\displaystyle {\tfrac {\\sqrt{2}}\pi$$$$z($z$)\}.$

미타그-레플러의 일체형 표현

미타그-레플러 함수의 통합 표현은 ( )의 6절이다.

${\displaystyle E_{\alpha ,\beta }(z)={\frac {1}{2\pi i}}\oint _{C}{\frac {t^{\alpha -\beta }e^{t}}{t^{\alpha }-z}}\,dt,\Re (\alpha )>0,\Re (\beta )>0,}$

여기서 등고선 C는 -118에서 시작하고 끝나며 통합체의 특이점과 분기점을 중심으로 원을 그린다.

라플라스 변환 및 미타그-레플러 합계와 관련된 표현(m=0을 사용한 Eq (7.5))^[1]

${\displaystyle \int _{0}^{\infty }e^{-tz}t^{\beta -1}E_{\alpha ,\beta }(\pm r\,t^{\alpha })\,dt={\frac {z^{\alpha -\beta }}{z^{\alpha }\mp r}},\Re (z)>0,\Re (\alpha )>0,\Re (\beta )>0.}$

미타그-레플러 함수의 응용

미타그-레플러 함수의 적용 중 하나는 점탄성 재료를 부분 순서에 따라 모델링하는 것이다.점탄성 물질의 시간 의존적 이완 거동에 대한 실험적 연구는 이완 과정 초기에 스트레스가 매우 빠르게 감소하고 상당 시간 동안 극도로 느린 붕괴가 특징이다.일정한 무증상 값에 도달하기까지 오랜 시간이 걸릴 수도 있다.따라서 충분한 정확도로 이완 행동을 기술하기 위해서는 많은 맥스웰 요소가 필요하다.이것은 많은 재료 매개변수를 식별하기 위해 어려운 최적화 문제로 끝난다.한편, 수년 동안, 점탄성 이론에 부분파생상품의 개념이 도입되었다.이러한 모델 중, 소수 재료 매개변수만으로 고무 재질의 동적 특성을 예측하는 데 부분 제너 모델이 매우 효과적인 것으로 밝혀졌다.해당 구성 방정식의 해법은 미타그-레플러 유형의 이완 함수로 이어진다.그것은 부정적인 주장으로 파워 시리즈에 의해 정의된다.이 함수는 임의의 연속 신호에 의해 원점에서 점프를 하는 이완 과정의 모든 필수 특성을 나타낸다.^[3][4]

참고 항목

• 미타그-레플러 합계
• 미타그-레플러 분포
• 폭스-라이트 함수

메모들

• 거텍 길, 피터 스트라카의 R 패키지 '미타그렐레플레R'Mittag-Leffler 함수, 분포, 랜덤 변수 생성 및 추정 구현.

참조

이 글은 일반적인 참고문헌 목록을 포함하고 있지만, 그에 상응하는 인라인 인용구가 충분하지 않다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오.(2021년 5월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

• 미타그-레플러, M.G.Sur la nouvelle ponpection E(x).C. R. 아카드.과학. 파리 137, 554–558 (1903)
• 미타그-레플러, M.G.Sopra la funzione E˛.x/.렌드 R. 액센트린시, (5세) 13, 3–5 (1904)
• Gorenflo R, Kilbas A.A, Mainardi F, Rogosin S.V, Mittag-Leffler Functions, 관련 주제 및 애플리케이션(Springer, New York, 2014) 443페이지 ISBN 978-3-662-4399-6
• Igor Podlubny (1998). "chapter 1". Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications. Mathematics in Science and Engineering. Academic Press. ISBN 0-12-558840-2.
• Kai Diethelm (2010). "chapter 4". The analysis of fractional differential equations: an application-oriented exposition using differential operators of Caputo type. Lecture Notes in Mathematics. Heidelberg and New York: Springer-Verlag. ISBN 978-3-642-14573-5.

외부 링크

• Mittag-Leffler 함수: MATLAB 코드
• Mittag-Leffler 및 안정적인 난수: 연속 시간 무작위 보행 및 공간 시간 분율 확산 방정식의 확률적 솔루션

이 글에는 크리에이티브 커먼스 귀속/공유 앨리케 라이센스에 따라 라이센스가 부여된 PlanetMath의 미탁-레플러 함수의 자료가 통합되어 있다.