정전기

에 관한 기사들
전자기학
전기 자력 광학 역사 교재
정전기 전하 쿨롱의 법칙 지휘자 전하밀도 유전율 전기 쌍극자 모멘트 전기장 전위 전기유속/전위에너지 정전 방전 가우스의 법칙 인덕션 절연체 분극밀도 정전기 마찰전기
자기정전학 앙페르의 법칙 비오사바르트 법칙 가우스의 자기 법칙 자기장 자속 자기 쌍극자 모멘트 투자율 자기 스칼라 퍼텐셜 자화 자기벡터퍼텐셜 오른손 규칙
전기역학 로렌츠 힘 법칙 전자기 유도 패러데이의 법칙 렌츠의 법칙 변위전류 맥스웰 방정식 전자기장 전자기 펄스. 전자기 복사 라모르 공식 브렘스스트랄룽 사이클로트론 복사 싱크로트론 복사 맥스웰 텐서 포인팅 벡터 리아나드-위허트 퍼텐셜 제피멘코 방정식 와류 런던 방정식 전자기장에 대한 수학적 설명
전기망 교류 정전용량 직류 전류 전기 분해 전류밀도 줄 가열 기전력 임피던스 인덕턴스 옴의 법칙 병렬 회로 저항 공진 공동 직렬 회로 전압 도파관
자기회로 자이레이터-콘덴서 모델 자기복합기저항 자기저항 자기력 투과성
공변 공식 전자기 텐서 (stress–에너지 텐서) 사류 전자기 포텐셜
사이언티스트 암페르 비옷 쿨롱 데이비 아인슈타인 패러데이 피조 가우스 헤비사이드 핸리다. 헤르츠 홉킨스 제피멘코 줄 켈빈 렌츠 리나르 로렌츠 맥스웰 노이만 외르스테드 옴 포인팅 리치 사바트 가수. 슈타인메츠 테슬라 볼타 웨버 비허트 포아송
v t

정전기는 느리게 움직이는 전하나 정지한 전하를 연구하는 물리학의 한 분야입니다.

고전 시대 이래로, 호박과 같은 어떤 물질들은 문지른 후에 가벼운 입자들을 끌어당기는 것으로 알려져 왔습니다.그래서 '전기'라는 단어는 그리스어로 호박을 뜻하는 ἤλεκτρον(Lektron)에서 유래된 것입니다.정전기 현상은 전하가 서로에게 작용하는 힘으로 발생합니다.그러한 힘은 쿨롱의 법칙으로 설명됩니다.

포장에서 분리한 후 랩을 손으로 끌어당기는 간단한 현상부터 곡물 사일로의 명백한 자발적 폭발, 제조 중 전자 부품의 손상, 복사기 및 레이저 프린터 작동에 이르기까지 많은 정전기 현상의 예가 있습니다.예를 들어, 수소 원자를 구성하는 전자와 양성자 사이의 힘은 그들 사이에서 작용하는 중력보다 약 36배 더 강력합니다.크기가 작기 때문에 전자와 양전하를 띤 핵 사이의 쿨롱 힘은 원자와 분자의 작용에 매우 큰 역할을 합니다.

쿨롱의 법칙

쿨롱의 법칙은 다음과 같습니다.^[5]

두 점전하 사이의 인력이나 반발력의 크기는 전하 크기의 곱에 정비례하고 두 점전하 사이의 거리의 제곱에 반비례합니다.'

힘은 그들과 합류하는 직선을 따라 있습니다.만약 두 전하가 같은 부호를 가지고 있다면, 두 전하 사이의 정전기적 힘은 반발력이고, 서로 다른 부호를 가지고 있다면, 두 전하 사이의 힘은 매력적입니다.

$r{\displaystyle }$ ${\displaystyle r}$이(가) 두 전하 사이의 거리(미터 단위)라면$$ 두 전하 $q{\displaystyle }${\$displaystyle q}$과 Q$${\$displaystyle$ Q$}$ 사이의 힘(뉴턴 단위)은 다음과 같습니다($$쿨롬비 단위).

${\displaystyle F={\frac {1}{4\pi \varepsilon _{0}}{\frac {qQ}{r^{2}}=k_{\text{e}}{\frac {qQ}{r^{2}}\,,}$

여기서 ε는 진공 유전율 또는 자유 공간의 유전율입니다.

${\displaystyle \varepsilon _{0}\approx \mathrm {8.854\187\817\times 10^{-12}~C^{2}{\cdot }N^{-1}{\cdot }m^{-2}.}$

ε의 SI 단위는 동등하게 A ⋅ ⋅kg ⋅m 또는 C ⋅N ⋅m 또는 F ⋅m입니다.쿨롱 상수는 다음과 같습니다.

${\displaystyle k_{\text{e}}={\frac {1}{4\pi \varepsilon _{0}}\approx \mathrm {8.987\551\792\times 10^{9}~N{\cdot }m^{2}{\cdot }C^{-2}.}$

단일 양성자는 e의 전하를 가지고 있고, 전자는 -e의 전하를 가지고 있습니다.

${\displaystyle e=\mathrm {1.602\176\634\times 10^{-19}~C}.}$

이러한 물리 상수(ε, k, e)는 현재 e가 정확히 정의되고 ε와 k는 측정된 양입니다.

전기장

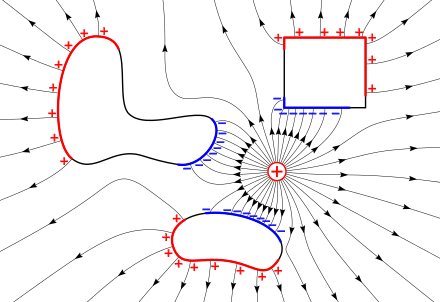
전기장인 $E$ → ${\displaystyle {\vec {E}},$쿨롱당 뉴튼 또는 미터당 볼트 단위는 점전하의 위치(무한으로 발산되는 곳)를 제외한 모든 곳에서 정의할 수 있는 벡터장입니다.쿨롱의 법칙에 의한 지점의 가상적인 작은 시험 전하에 대한 뉴튼에서의 정전기력 $F$ → $displaystyle {\vec {F}\,}$를 쿨롱에서의 전하 $q$ ${\displaystyle q\,}$의 크기로 나눈 것으로 정의됩니다.

${\displaystyle {\vec {E}}={{\vec {F} \over q}$

전기장 선은 전기장을 시각화하는 데 유용합니다.필드 라인은 양전하에서 시작하여 음전하에서 종료됩니다.이들은 각 점에서 전기장의 방향과 평행하며, 이들 전기장 선의 밀도는 주어진 점에서 전기장의 크기를 나타내는 척도입니다.

$점$ $r$ → ${\displaystyle i_{}}$ ${\displaystyle {\vec {r}}_{i}($소스 점이라고 함)에 위치한$$$N개$의 전하 ${\displaystyle N$$}$개의 입자 ${\displaystyle {집합}_{}}$을 고려하십시오. $r$ → ${\displaystyle {\vec {r}}($필드 점이라고 함)에 있는 전기장은 다음과 같습니다.

${\displaystyle {\vec {E}}({\vec {r}})={\frac {1}{4\pi \varepsilon _{0}}\sum _{i=1}^{N}{\frac {{\mathcal {R}}_{i}Q_{i}}{\left\{\mathcal {\vec {R}}_{i}\right\^{2}}}$

여기서 $R$ → ${\displaystyle i}$ = r →${\displaystyle }$- ${\displaystyle r_{}}$ → i${\displaystyle {}_{}}$ ${\displaystyle {\mathcal {R}}_{i}$=${\vec {r}}-{\vec$ {$r}_{i}}$는 소스 포인트 $r$ → ${\displaystyle i_{}}$ ${\displaystyle {\vec {r}_{i}$에서 필드 포인트 $r$ → ${\vec {r}}$로 이동 벡터입니다$.$그리고 $R$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle i_{}}$ = ${\displaystyle {}_{}}$ → ${\displaystyle i_{}}$ /${\displaystyle {}_{}}$‖ ${\displaystyle {}_{}}$ → ${\displaystyle i_{}}$ ‖ ${\displaystyle {\widehat {\mathcal {R}}_{i}$=${\vec {\mathcal {R}}_{i}/\left\{\vec {\mathcal {R}}_{i}\right\}$는 필드의 방향을 나타내는 단위 벡터입니다.원점에서 단일 점 전하의 경우, 이 전기장의 $크기$는 E${\displaystyle }$= ${\displaystyle {}_{}}$Q / ${\displaystyle R}$ ${\displaystyle 2^{}}${\$displaystyle$ E = $k_{\text{e}}Q/{\mathcal {R}}^{2},$ 양이면 해당 전하에서 떨어진 점입니다.힘(그리고 따라서 장)은 개별 소스 입자로 인한 모든 기여를 합산하여 계산할 수 있다는 사실은 중첩 원리의 한 예입니다.전하 분포에 의해 생성된 전기장은 부피 전하 밀도 ρ${\displaystyle (r}$ →${\displaystyle }$) ${\displaystyle \rho({\vec {r})}}$로 주어지며, 이 합을 3중 적분으로 변환하여 얻을 수 있습니다.

${\displaystyle {\vec {E}}({\vec {r}})={\frac {1}{4\pi \varepsilon _{0}}\iiint {\frac {\vec {r}}-{\vec {r}\',}{\left\{\vec {r}}-{\vec {r}\',\right\^{3}}\rho({\vec {r}\')\",\mathrm {d}^{3}r\',}$

가우스의 법칙

가우스의 법칙은^[9][10] "전기장에 그려지는 어떤 모양의 자유공간에서 닫힌 표면을 통과하는 전기의 총 흐름은 표면에 둘러싸인 전기의 총 전하에 비례합니다."라고 명시합니다.많은 수치 문제들은 a를 고려함으로써 해결될 수 있습니다.

물체 주위의 가우시안 표면수학적으로, 가우스의 법칙은 적분 방정식의 형태를 갖습니다.

${\displaystyle \point _{S}{\vec {E}}\cdot \mathrm {d}{\vec {A}}={\frac {1}{\varepsilon _{0}}\,Q_{\text{closed}}=\int _{V}{\rho \over \varepsilon _{0}}\cdot \mathrm {d}^{3}r,}$

여기서 ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ = ${\displaystyle d}$ x ${\displaystyle d}$ ${\displaystyle \text{y}}$ ${\displaystyle d}$ z ${\displaystyle \mathrm {d}^{3}r$=\$mathrm {d} x\\mathrm {d}$ y$\\mathrm {d} z}$는 볼륨 요소입니다.전하가 표면 위나 선을 따라 분포하는 경우, ρ d ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle \rho \,\mathrm {d}^{3}r을$σ ${\displaystyle d}$ ${\displaystyle A}$ ${\displaystyle \sigma \,\mathrm {d}$ A $또는$ λ d ℓ ${\displaystyle \lambda \,\mathrm {d} \ell }$로 대체합니다$.$ 발산 정리는 가우스의 법칙을 미분 형식으로 쓸 수 있게 해줍니다.

${\displaystyle {\vec {\nabla}}\cdot {\vec {E}}={\rho \over \varepsilon _{0}}}$

여기서 ∇ → ⋅ ${\displaystyle {\vec {\nabla}}\cdot }$은(는) 발산 연산자입니다.

포아송 방정식과 라플라스 방정식

정전기 전위의 정의는 가우스 법칙의 미분 형식(위)과 결합하여 전위 φ과 전하 밀도 ρ 사이의 관계를 제공합니다.

${\displaystyle {\nabla}^{2}\phi = - \rho \over \varepsilon _{0}}}$

이 관계는 포아송 방정식의 한 형태입니다.^[11]짝을 이루지 않은 전하가 없을 경우, 방정식은 라플라스 방정식이 됩니다.

${\displaystyle {\nabla}^{2}\phi = 0,}$

정전기 근사

정전기 근사치의 유효성은 전기장이 비회전 상태라는 가정에 달려 있습니다.

${\displaystyle {\vec {\nabla}}\times {\vec {E}}=0.}$

패러데이의 법칙에 따르면, 이 가정은 시간에 따라 변하는 자기장의 부재 또는 거의 부재를 의미합니다.

${\displaystyle {\partial {\vec {B}} \over \partial t}=0.}$

다시 말해서, 정전기는 자기장이나 전류의 부재를 필요로 하지 않습니다.오히려, 자기장이나 전류가 존재한다면, 그것들은 시간에 따라 변하지 않아야 합니다, 또는 최악의 경우, 그것들은 시간에 따라 매우 천천히 변해야만 합니다.일부 문제에서는 정확한 예측을 위해 정전기와 자기 정전기가 모두 필요할 수 있지만 둘 사이의 결합은 여전히 무시될 수 있습니다.정전기와 자기기전은 전자기학에 대한^[12] 비상대론적 갈릴레이 한계로 볼 수 있습니다.

정전 전위

전기장이 비회전이므로 전기장을 정전기 전위(전압이라고도 함)라고 하는$$스칼라 함수 ϕ ${\displaystyle \phi}$의 기울기로 표현할 수 있습니다.전기장, $E{\displaystyle }$ ${\displaystyle E}$는$$높은 전기퍼텐셜 영역에서 낮은 전기퍼텐셜 영역으로 수학적으로 다음과 같이 표현됩니다.

${\displaystyle {\vec {E}}=-{\vec {\nabla}}\phi .}$

기울기 정리를 사용하여 전하를 ${\displaystyle a}$ $지점$에서 ${\displaystyle b}$ 지점으로 이동하는 데 필요한 단위 전하당 작업량을 정전기 전위로 정의할 수 있습니다.

${\displaystyle -\int _{a}^{b}{{\vec {E}}\cdot \mathrm {d}{\vec {\ell}}}=\phi({\vec {b}})-\phi({\vec {a}}).$

이 식들로부터, 우리는 전기장이 사라지는 영역에서 전기 퍼텐셜이 일정하다는 것을 알 수 있습니다(예를 들어 전도성 물체 내부에서 일어나는 것).

정전기 에너지

테스트 입자의 위치 에너지인 ${\displaystyle {UE}_{}^{}}$ ${\displaystyle {\text{단일}}_{}^{}}$ ${\displaystyle U_{\mathrm {E} ^{\text{single}}$는$$일의 선분에서 계산할 수 있으며, $q$ n ${\displaystyle {}_{}}$ → ⋅ ${\displaystyle d}$ → ${\displaystyle q_{n}{\vec {E}}\cdot \mathrm {d} {\vec {\ell$ 무한대의 한 점에서 적분하고, $전하$ $Q$ ${\displaystyle n_{}}$ ${\$$displaystyle$ $N}$개의 입자 집합을 가정합니다$.$$ystyle Q_{n$ 이미 $r$ $→$ ${\displaystyle i_{}}$ ${\displaystyle {\vec {r}_{i}$ 지점에 있습니다$.$이 퍼텐셜 에너지(줄 단위)는 다음과 같습니다.

${\displaystyle U_{\mathrm {E}}^{\text{single}}=q\phi({\vec {r})={\frac {q}{4\pi \varepsilon _{0}}\sum_{i=1}^{N}{\frac {Q_{i}}{\left\{\mathcal {\vec {R}}\right\}}$

여기서 ${\displaystyle \stackrel{}{{Ri}_{}}}$ → ${\displaystyle r}$ → -${\displaystyle {}_{}}$ → ${\displaystyle i_{}}$ ${\displaystyle {\mathcal {R_{i}}}$=${\vec {r}-{\vec {r}_{i$$}}$는 각 $전하$의 ${\displaystyle {거리}_{}}$입니다$.$ $이$는 r → ${\displaystyle {\vec {r$ϕ(${\displaystyle r}$→${\displaystyle \stackrel{}{}}$) ${\displaystyle$ \$phi({\vec$ {$r}})}은($는) 테스트 전하가 없을 $경우$ r → {\$displaystyle${\$vec$ {r$}}$에 해당하는 전위입니다.전하가 두 개만 존재할 경우 전위 에너지는 ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ Q ${\displaystyle {2\mathrm{}}_{}}$/ ${\displaystyle r}${\$displaystyle k_{\text{e}}$입니다.$Q_{1}Q_{2}/r$ N개의 전하 집합에 의한 총 전기 퍼텐셜 에너지는 이 입자들을 한 번에 하나씩 조립하여 계산합니다.

${\displaystyle U_{\mathrm {E} }^{\text{total}}={\frac {1}{4\pi \varepsilon _{0}}\sum _{j=1}^{j}\sum _{i=1}^{\frac {Q_{i}}{r_{ij}}={\frac {1}{2}}\sum _{i=1}^{N}Q_{i}\phi _{i}}$

여기서 다음의 합 j = 1 ~ N은 i = j를 제외합니다.

${\displaystyle \phi _{i}={\frac {1}{4\pi \varepsilon _{0}}\sum _{\stackrel {j=1}{j\neq i}}^{N}{\frac {Q_{j}}{r_{ij}}}}$

이 전위인 ϕ i ${\displaystyle \phi_{i}}$는 전하 ${\displaystyle {Qi}_{}}$ ${\displaystyle Q_{i}$가 누락된 경우 $r$ → ${\displaystyle i_{}}$ ${\displaystyle {\vec {r}_{i}$에서 측정되는 전위입니다.이 공식은 분산된 전하 구름에서 각 점 전하를 조립하는 데 필요한 (무한) 에너지를 분명히 제외합니다.전하의 합은 처방 ∑ $($⋯$)$→ ∫ $($⋯$)$ρ $d$ ${}^{}$ r ${\textstyle \sum (\cdots)\rightarrow \int (\cdots)\rho \,\mathrm {d}^{3}r$

${\displaystyle U_{\mathrm {E}}^{\text{total}}={\frac {1}{2}}\int \rho({\vec {r})\phi({\vec {r})\,\mathrm {d}^{3}r={\frac {\varepsilon _{0}}{2}\int \left {\mathbf {E}\right ^{2}\,\mathrm {d}^{3}r,}$

정전기 에너지에 대한 이 두 번째 표현은 전기장이 전기 퍼텐셜의 음의 기울기라는 사실과 부품별 적분과 유사한 방식으로 벡터 미적분학적 항등식을 사용합니다.전기장 에너지에 대한 이 두 적분은 정전기 에너지 밀도에 대한 두 개의 상호 배타적 공식을 나타내는 것처럼 보입니다.즉, $\frac{12}{}$ ρ ϕ ${\textstyle {\frac {1}{2}}\rho \phi}$와 $\frac{12}{}$ ε 0 $E_{}$ $2^{}$ ${\textstyle {\frac {1}{2}}\varepsilon _{0}E^{2};$이 둘이 모든 공간에 걸쳐 통합된 경우에만 전체 정전기 에너지에 대해 동일한 값을 산출합니다.

정전압

도체에서 표면 전하는 전기장이 있을 때 힘을 경험합니다.이 힘은 표면 전하에서 불연속적인 전기장의 평균입니다.지표면 바로 바깥쪽에 있는 필드의 평균은 다음과 같습니다.

${\displaystyle P={\frac {\varepsilon _{0}}{2}}E^{2}}$

이러한 압력은 표면 전하의 부호에 관계없이 도체를 필드 안으로 끌어당기는 경향이 있습니다.

참고 항목

• 전자기 – 하전 입자 간의 근본적인 상호작용
• 정전기 발전기, 정전기를 만드는 기계.
• 정전기 유도, 전기장에 의한 전하 분리
• 유전율과 상대 유전율, 물질의 전기 분극성.
• 전하의 양자화, 전자 또는 양성자가 운반하는 전하 단위.
• 정전기, 물질에 축적된 정지 전하.
• 마찰 전기 효과, 미끄러짐 또는 접촉으로 인한 전하 분리

참고문헌

추가열람

• Hermann A. Haus; James R. Melcher (1989). Electromagnetic Fields and Energy. Englewood Cliffs, NJ: Prentice-Hall. ISBN 0-13-249020-X.
• Halliday, David; Robert Resnick; Kenneth S. Krane (1992). Physics. New York: John Wiley & Sons. ISBN 0-471-80457-6.
• Griffiths, David J. (1999). Introduction to Electrodynamics. Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-805326-X.

외부 링크

• Wikimedia Commons의 정전기 관련 매체

• 파인만의 물리학 강의 제1권제2장 제4장: 정전기
• 정전기학 개론:포인트 전하는 디랙 델타 함수를 사용하여 분포로 처리할 수 있습니다.

라이브러리 리소스정보 정전기

라이브러리의 리소스

Wik University의 정전기 관련 학습 자료