A* 검색 알고리즘

A* search algorithm
학급검색 알고리즘
data 구조그래프
최악의 경우 성능
최악의 경우 공간의 복잡성
그래프와 트리
검색 알고리즘
최단 경로
리스트
관련 토픽

A*('A-star'로 발음)는 그래프 트래버설 및 경로 검색 알고리즘으로, 완전성, 최적성 및 최적의 [1]효율성으로 인해 컴퓨터 과학의 여러 분야에서 자주 사용됩니다.된 모든 노드를 메모리에 저장하기 때문에 Od O 공간이 복잡하다는 실질적인 단점이 있습니다.따라서 실제 여행 라우팅 시스템에서는 일반적으로 더 나은 [2]성능을 얻기 위해 그래프를 미리 처리할 수 있는 알고리즘과 메모리 경계 접근법에 의해 성능이 향상되지만, 많은 [3]경우 A*는 여전히 최고의 솔루션입니다.

스탠포드 연구소(현재의 SRI International)의 피터 하트, 닐슨, 버트람 라파엘은 [4]1968년에 이 알고리즘을 처음 발표했다.이는 다이크스트라 알고리즘의 확장으로 볼 수 있다.A*는 휴리스틱스를 사용하여 검색을 안내함으로써 성능을 향상시킵니다.

Dijkstra 알고리즘과 비교하여 A* 알고리즘은 지정된 소스에서 지정된 목표까지의 최단 경로만 찾고 지정된 소스에서 가능한 모든 목표까지의 최단 경로 트리는 찾지 않습니다.이것은 특정 목표 지향 휴리스틱을 사용하기 위해 필요한 트레이드오프입니다.Dijkstra 알고리즘에서는 전체 최단 경로 트리가 생성되기 때문에 모든 노드가 목표이며 특정 목표 지향 휴리스틱은 존재할 수 없습니다.

역사

A*는 Shakey the Robot의 경로 계획을 연구하는 연구자들에 의해 발명되었습니다.

A*는 독자적인 액션을 계획할 수 있는 모바일 로봇을 만드는 것을 목적으로 한 Shakey 프로젝트의 일환으로 작성되었습니다.Nils Nilsson은 원래 Shakey의 경로 [6]계획에 Graph Traverser 알고리즘을[5] 사용할 것을 제안했습니다.그래프 트래버서는 노드 n에서 목표 노드까지의 추정 거리인 휴리스틱 함수 h(n)에 의해 유도됩니다.이 함수는 시작 노드부터n까지의 거리인 g(n)를 완전히 무시합니다.Bertram Raphael은 g(n) + h(n)[6]의 합을 사용할 것을 제안했다.피터 하트는 현재 우리가 휴리스틱 함수의 수용성과 일관성이라고 부르는 개념을 발명했다.A*는 원래 경로 비용이 비용의 합계일 때 최소 비용 경로를 찾기 위해 설계되었지만 A*를 사용하여 비용 대수 [7]조건을 충족하는 문제에 대한 최적의 경로를 찾을 수 있는 것으로 나타났습니다.

원래 1968년 A[4]* 논문에는 휴리스틱 함수가 일관되고 A*의 동점 해소 규칙을 적절히 선택하면 A*보다[a] 적은 노드를 확장할 수 없다는 정리가 포함되어 있었습니다.A″correction″ 몇년 later[8]이 일관성 요구되지 않았던다고 주장하면서 이 A*의 최적성(지금 최적의 효율성이라고 불리는)의지만 일관되지 않는 임의로 더 많은 노드는 alternat보다 허용은 heuristic과 A*의 예를 들었죠 Dechter와 펄의 결정판 연구에서 거짓임을 보여 준 것 출판되었다.ive A*와 같은 알고리즘.[9]

묘사

랜덤으로 생성된 미로를 탐색하는 A* 경로 탐색 알고리즘
그래프에서 두 점 사이의 경로를 찾기 위한 A* 검색의 그림입니다.

A*는 정보 검색 알고리즘, 즉 베스트 퍼스트 서치로서, 가중 그래프에 근거해 공식화되어 있습니다.그래프의 특정 시작 노드에서 시작하여 최소 비용(최소 이동 거리, 최단 시간 등)을 가진 특정 목표 노드에 대한 경로를 찾는 것을 목적으로 합니다.이를 위해 시작 노드에서 시작되는 경로 트리를 유지하고 종료 기준이 충족될 때까지 이러한 경로를 한 번에 한 에지씩 확장합니다.

메인 루프를 반복할 때마다 A*는 어떤 경로를 확장할지 결정해야 합니다.이는 경로 비용과 목표까지 경로를 확장하는 데 필요한 비용의 견적을 기반으로 합니다.특히, A*는 다음 중 하나를 최소화하는 경로를 선택하여

여기서 n은 경로상의 다음 노드, g(n)는 시작 노드에서n까지의 경로 비용, h(n)는 n에서 목표까지의 가장 저렴한 경로 비용을 추정하는 경험적 함수입니다.A*는 확장하기로 선택한 경로가 시작에서 목표까지의 경로이거나 확장 대상이 되는 경로가 없는 경우 종료됩니다.휴리스틱 함수는 문제에 따라 다릅니다.발견적 함수가 허용 가능한 경우(즉, 목표에 도달하기 위한 실제 비용을 과대평가하지 않음) A*는 처음부터 목표까지 최소 비용 경로를 반환할 수 있습니다.

A*의 일반적인 구현에서는 priority 큐를 사용하여 최소(추정) 비용 노드를 반복적으로 선택하여 확장합니다.이 priority 큐는 오픈세트 또는 프린지라고 불립니다.알고리즘의 각 단계에서 f(x) 값이 가장 작은 노드가 큐에서 삭제되고 그에 따라 네이버의 f 및 g 값이 갱신되어 이들 네이버가 큐에 추가됩니다.알고리즘은 삭제된 노드(즉, 모든 프린지 노드 중 f 값이 가장 낮은 노드)가 목표 [b]노드가 될 때까지 계속됩니다.목표의 h는 허용 가능한 휴리스틱에서 0이기 때문에 이 목표의 f 값은 최단 경로의 비용이기도 하다.

지금까지 설명한 알고리즘에서는 최단 경로의 길이만 알 수 있습니다.실제 스텝 시퀀스를 찾기 위해 경로상의 각 노드가 이전 노드를 추적하도록 알고리즘을 쉽게 변경할 수 있습니다.이 알고리즘이 실행된 후 종료 노드는 일부 노드의 이전 노드가 시작 노드가 될 때까지 이전 노드를 가리킵니다.

예를 들어 지도에서 최단 루트를 검색할 때 h(x)는 목표까지의 직선 거리를 나타낼 수 있습니다.이는 물리적으로 두 지점 사이의 거리가 가장 작기 때문입니다.비디오 게임의 그리드 맵에서는 사용 가능한 움직임 세트(4방향 또는 8방향)에 따라 맨해튼 거리 또는 8진수 거리를 사용하는 것이 좋습니다.

휴리스틱 h가 그래프의 모든 에지(x, y)에 대한 추가 조건 h(x) d d(x, y) + h(y)를 만족하는 경우(여기서 d는 해당 에지의 길이를 나타냄), h는 단조 또는 일관성이 있다고 합니다.일관된 휴리스틱을 통해 A*는 노드를 두 번 이상 처리하지 않고 최적의 경로를 찾을 수 있으며 A*는 비용 d'(x, y) = d(x, y) + h(y) - h(x)로 Dijkstra의 알고리즘을 실행하는 것과 동일합니다.

유사 코드

다음 의사 코드는 알고리즘에 대해 설명합니다.

기능. reconstructure_path(발신기지, 현재의)     total_path := {current}     하는 동안에 현재의 에 발신기지.열쇠들.:         현재의 := 발신기지[현재의]         total_path.프리펜드(현재의)     돌아가다 total_path  // A*는 시작에서 목표까지의 경로를 찾습니다. // h는 휴리스틱 함수입니다.h(n)는 노드n에서 목표에 도달하기 위한 비용을 추정합니다. 기능. A_Star(개시하다, 목표, h)     // (다시) 확장해야 할 수 있는 검색된 노드 세트입니다.     // 처음에는 시작 노드만 알려져 있습니다.     // 이것은 보통 해시 집합이 아닌 min-heap 또는 priority 큐로 구현됩니다.     오픈 세트 := {start}      // 노드 n의 경우 comeFrom[n]은 시작부터 가장 저렴한 경로에서 바로 앞에 있는 노드입니다.     // ~ n 현재 알려져 있습니다.     발신기지 := 한 사람 빈 지도      // 노드 n의 경우 gScore[n]는 시작부터 n까지의 현재 알려진 가장 저렴한 경로의 비용입니다.     g스코어 := 지도 와 함께 체납 가치 의 Infinity     g스코어[개시하다] := 0      // 노드 n의 경우 fScore[n] := gScore[n] + h(n)입니다.fScore[n]는 다음과 같은 현시점에서의 최선의 추측을 나타냅니다.     // 경로가 n을 통과할 경우 처음부터 끝까지 얼마나 저렴할 수 있는지.     fScore := 지도 와 함께 체납 가치 의 Infinity     fScore[개시하다] := h(개시하다)      하는 동안에 오픈 세트 이 것은 아니다. 빈         // openSet이 최소 히프 또는 priority 큐인 경우 이 작업은 O(Log(N) 시간 내에 발생할 수 있습니다.         현재의 := 그 노드 에 오픈 세트 하고 있다 그 최저의 fScore[] 가치         한다면 현재의 = 목표             돌아가다 reconstructure_path(발신기지, 현재의)          오픈 세트.제거한다.(현재의)         위해서 각각 인접국 의 현재의             // d(current, controll)는 전류에서 네이버까지의 엣지 무게입니다.             // primative_gScore는 시작부터 네이버까지의 전류까지의 거리입니다.             잠정_g스코어 := g스코어[현재의] + d(현재의, 인접국)             한다면 잠정_g스코어 < > g스코어[인접국]                 // 이 네이버 경로는 이전 경로보다 우수합니다.녹음해!                 발신기지[인접국] := 현재의                 g스코어[인접국] := 잠정_g스코어                 fScore[인접국] := 잠정_g스코어 + h(인접국)                 한다면 인접국 것은 아니다. 에 오픈 세트                     오픈 세트.더하다(인접국)      // 열린 집합이 비어 있지만 목표에 도달하지 못했습니다.     돌아가다 실패.

비고: 이 의사코드에서는 노드가 1개의 경로로 도달하여 openSet에서 삭제되고 이후 더 저렴한 경로로 도달하면 다시 openSet에 추가됩니다.이는 경험적 함수가 허용 가능하지만 일관성이 없는 경우 반환되는 경로가 최적이 되도록 보장하는 데 필수적입니다.휴리스틱이 일관성이 있는 경우 노드가 openSet에서 삭제될 때 경로가 최적이므로 노드에 다시 도달하면 'tentative_gScore < gScore [ neighbor ]' 테스트는 항상 실패합니다.

로봇 모션 계획 문제에서 시작 노드에서 목표 노드까지의 경로를 찾기 위한 A* 검색의 그림입니다.빈 원은 개방형 집합의 노드, 즉 탐색해야 할 노드를 나타내며 채워진 원은 닫힌 집합에 있습니다.닫힌 각 노드의 색상은 목표로부터의 거리를 나타냅니다.녹색일수록 가깝습니다.먼저 A*가 목표 방향으로 직선 방향으로 이동하는 것을 볼 수 있으며, 장애물에 부딪히면 오픈 세트에서 노드를 통과하는 대체 경로를 탐색할 수 있습니다.
다음 항목도 참조하십시오.다이크스트라 알고리즘


예

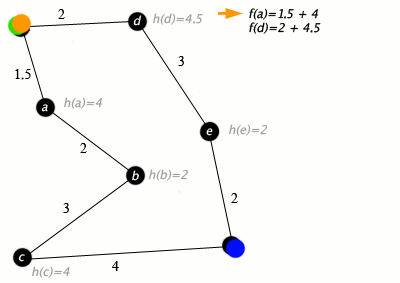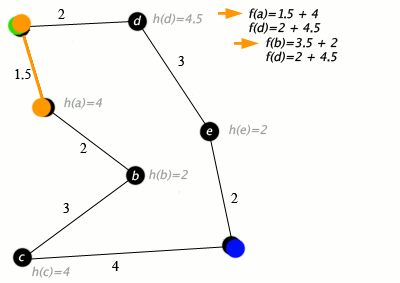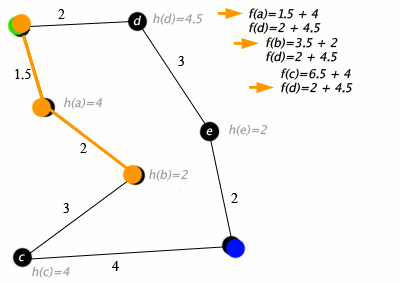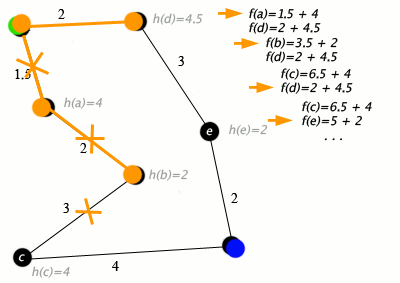
노드가 도로와 연결된 도시이고 h(x)가 목표 지점까지의 직선 거리인 A* 알고리즘의 예:

An example of A* algorithm in action (nodes are cities connected with roads, h(x) is the straight-line distance to target point) Green: Start, Blue: Target, Orange: Visited

키: 녹색: 시작, 파란색: 목표, 주황색: 방문

A* 알고리즘에는 실제 애플리케이션도 있습니다.이 예에서 가장자리는 철도이며 h(x)는 표적에 대한 대원 거리(구면상의 가능한 최단 거리)입니다.이 알고리즘은 워싱턴 D.C.와 로스앤젤레스 사이의 경로를 찾고 있다.

The A* algorithm finding a path of railroads between Washington, D.C. and Los Angeles.

구현 상세

A* 구현의 성능에 큰 영향을 미칠 수 있는 간단한 최적화 또는 구현 세부 사항이 많이 있습니다.첫 번째로 주의할 점은 priority 큐가 tie를 처리하는 방식이 상황에 따라 퍼포먼스에 큰 영향을 미칠 수 있다는 것입니다.큐가 LIFO 방식으로 동작하도록 동점이 깨지면 A*는 등가 비용 경로에서 깊이 우선 검색처럼 작동합니다(등가 최적 솔루션 두 개 이상 탐색을 피함).

검색이 끝날 때 경로가 필요한 경우 각 노드에서 해당 노드의 상위 노드에 대한 참조를 유지하는 것이 일반적입니다.검색이 끝나면 이러한 참조를 사용하여 최적의 경로를 복구할 수 있습니다.이러한 참조가 유지되고 있는 경우는, 같은 노드가 priority 큐에 2회 이상 표시되지 않는 것이 중요합니다(각 엔트리는 노드에 대한 다른 패스에 대응하고 있으며, 각각의 비용은 다릅니다).여기서 표준적인 접근법은 추가하려는 노드가 priority 큐에 이미 표시되어 있는지 확인하는 것입니다.이 경우 priority 및 부모 포인터는 저비용 패스에 대응하도록 변경됩니다.표준 바이너리 힙 기반 priority 큐는 요소 중 하나를 검색하는 작업을 직접 지원하지 않지만 요소를 힙 내의 위치에 매핑하는 해시 테이블을 사용하여 확장할 수 있으므로 이 우선 순위 감소 작업을 로그 시간으로 수행할 수 있습니다.또는 Fibonacci 힙은 상각된 일정한 시간 내에 동일한 우선 순위 감소 작업을 수행할 수 있습니다.

특수한 경우

Dijkstra의 알고리즘은 균일한 비용 검색 알고리즘의 또 다른 예로서 A*의 특수한 경우로 볼 수 있다. 서 [10][11]모든 x에 대해( x ) { h)=이다. 일반적인 깊이 우선 검색은 매우 큰 값을 가진 글로벌 카운터 C가 있다는 점을 고려하여 A*를 사용하여 구현할 수 있다.노드를 처리할 때마다 새로 검출된 모든 네이버에 C를 할당합니다.각 할당 후 카운터 C를 1개씩 줄입니다.따라서 노드가 조기에 검출될수록 의 h h 값이 높아집니다.Dijkstra의 알고리즘과 깊이 우선 검색 모두 각 노드에 h 값을 포함하지 않고 보다 효율적으로 구현할 수 있습니다.

특성.

종료와 완전성

음수가 아닌 에지 가중치 A*를 갖는 유한 그래프에서는 종료가 보장되고 완전합니다. 즉, 솔루션(시작에서 목표까지의 경로)이 존재하면 항상 찾습니다. 분기 계수와 엣지 비용이 0( ( x,)> >> ( \ d ( , y \ )에서 제외된 무한 그래프에서는 A*는 솔루션이 [1]존재하는 경우에만 종료됩니다.

수용성

검색 알고리즘은 최적 해법을 반환하는 것이 보증되면 허용된다고 한다.A*에서 사용하는 휴리스틱 함수가 허용 가능한 경우 A*도 허용됩니다.이에 대한 직관적인 '증명'은 다음과 같습니다.

A*는 검색을 종료할 때 처음부터 끝까지 실제 비용이 오픈 노드(노드의 f 값)를 통과하는 경로의 예상 비용보다 낮은 경로를 찾았습니다.휴리스틱이 허용 가능한 경우 이러한 추정치는 낙관적이기 때문에(다음 단락 참조), A*는 이미 보유하고 있는 노드보다 더 저렴한 솔루션을 제공할 수 없기 때문에 이러한 노드를 무시해도 됩니다.즉, A*는 처음부터 목표까지의 저비용 경로의 가능성을 간과하지 않기 때문에 그러한 가능성이 존재하지 않을 때까지 검색을 계속할 것입니다.

휴리스틱이 허용되더라도 노드의 ff 값이 낙관적이라고 보장되지 않기 때문에 실제 증거는 조금 더 관련이 있다.이는 오픈 노드의g(\ g 이 최적임을 보장할 수 없기 때문에 g g의 합이 낙관적일 수 없기 때문입니다.

최적성과 일관성

P의 문제 P의 모든 문제 P와 Alts의 모든 알고리즘 A in에 대해 P의 해결 시에 A가 전개하는 노드 세트가 P의 해결 시에 A in가 전개하는 노드 세트의 서브셋(가능하면 동일)인 경우, 알고리즘 A는 문제 P의 집합 중 하나의 대체 알고리즘 Alts에 대해 최적으로 효율적이다.A*의 최적 효율에 대한 최종적인 연구는 Rina Dechter와 Judea [9]Pearl에 의한 것입니다.그들은 A*의 휴리스틱과 조합하여 Alts와 P의 다양한 정의를 단순히 허용되거나 일관성과 허용 둘 다로 간주했다.그들이 증명한 가장 흥미로운 긍정적인 결과는 일관된 휴리스틱을 가진 A*가 모든 "병리학적" 검색 문제에 대해 허용되는 모든 A* 유사 검색 알고리즘에 대해 최적으로 효율적이라는 것이다.대략적으로 말하면, 그들의 비병리적인 문제라는 개념은 지금 우리가 말하는 '연계 해제'의 의미이다.A*의 경험적 접근법이 허용 가능하지만 일관성이 없는 경우 이 결과는 유지되지 않습니다.이 경우 Dechter와 Pearl은 일부 비병리적인 문제에서 A*보다 임의로 적은 수의 노드를 확장할 수 있는 허용 가능한 A*와 유사한 알고리즘이 있음을 보여주었습니다.

최적의 효율성은 노드 확장 횟수(A*의 메인 루프 반복 횟수)가 아니라 확장된 노드 세트에 관한 것입니다.사용 중인 휴리스틱이 허용 가능하지만 일관성이 없는 경우 노드가 A*만큼 여러 번(최악의 [12]경우 기하급수적인 횟수) 확장될 수 있습니다.이러한 상황에서는 Dijkstra의 알고리즘이 A*를 크게 능가할 수 있습니다.그러나 보다 최근의 연구에 따르면 이 병리학적 사례는 검색 그래프의 가장자리 무게가 그래프의 크기에서 기하급수적인 특정 상황에서만 발생하며, 특정 일관성이 없는(그러나 허용 가능한) 휴리스틱스는 A*[13][14] 검색에서 노드 확장 수를 줄일 수 있다.

유계 완화

일관된 휴리스틱의 5.0(=120)배인 휴리스틱을 사용하고 차선의 경로를 얻는 A* 검색입니다.

허용도 기준은 최적의 솔루션 경로를 보장하지만, A*는 최적의 경로를 찾기 위해 동등하게 중요한 모든 경로를 검토해야 함을 의미합니다.대략적인 최단 경로를 계산하기 위해 허용성 기준을 완화하여 최적성을 희생하면서 검색 속도를 높일 수 있습니다.대부분의 경우 솔루션 경로가 최적의 솔루션 경로의 (1 + ))배보다 나쁘지 않음을 보장할 수 있도록 이러한 완화를 제한하고 싶습니다.이 새로운 보증은 「수용 가능」이라고 불립니다.

γ-허용 알고리즘은 다음과 같습니다.

  • 가중치 A*/[15]정적 가중치h(n)가 허용 가능한 휴리스틱 함수인 경우a 가중치 버전의 A* 검색에서는 h(n) = ha h(n), > > 1을 휴리스틱 함수로 사용하여w 평소처럼 A* 검색을 수행합니다(확장된 노드가 적기 때문에 결과적으로 h를 사용하는a 것보다 더 빠르게 수행됩니다).따라서 검색 알고리즘에 의해 검출된 패스의 비용은 [16]그래프 내의 최소 비용 경로의 최대 0.5배입니다.
  • 동적 Weighting[17]은 비용 함수 f(n))g(n)+(1+w(nε))h(n){f(n)=g(n)+(1+\varepsilon w(n))h(n)\displaystyle}, w(n)){1− d(n)Nd(n)≤ N0 다르{\displaystyle w(n)={\begin{경우}1-{\frac{d(n)}{N}}&d(n)\leq N\\0&,{\text{ 그렇지 않으면}}\end{경우}}}을 사용합니다.그리고 어디서 ( ){ d는 검색 깊이, N은 솔루션 경로의 예상 길이입니다.
  • Sampled Dynamic[18] Weighting에서는 노드의 샘플링을 사용하여 휴리스틱오류를 보다 정확하게 추정하여 디버깅합니다.
  • [19]는 두 가지 휴리스틱 함수를 사용합니다.첫 번째는 후보 노드를 선택하는 데 사용되는 FOCAL 목록이고 두 번째F h는 FOCAL 목록에서 가장 유망한 노드를 선택하는 데 사용됩니다.
  • A는ε[20] f( ) + F( Af ()+(을 가진 노드를 선택합니다.여기서 A와 B는 상수입니다.노드를 선택할 수 없는 경우 알고리즘은 f () + () { Cf ( ) + _ { （ ）} the thetracktracktracktracktracktrack with with with with with 。여기서 C와 D는 상수입니다.
  • AlphA*[21]는 최근 확장된 노드를 선호함으로써 깊이 우선 이용을 촉진하려고 합니다.AlphA*이 wα(n)){λ g(π(n))≤ g(n사이)Λ 그렇지 않으면{\displaystyle w_{\alpha}(n)={\begin{경우}\lambda 및 α(n))(1+wα(n))f(n){\displaystyle f_{\alpha}(n)=(1+w_{\alpha}(n))f(n)},;g(\pi(n))\leq g({\tilde{n}})\\\Lambda 및의;{\text{ 다른 비용 함수를 사용합니다.현명한}}){ 。여기서 와「」는 \ \Lambda의 상수, 「(n)」은 n의 부모, 「n」은 가장 최근에 전개된 노드입니다.

복잡성

A*의 시간 복잡도는 휴리스틱에 따라 달라집니다.무한 서치 공간의 최악의 경우 확장 노드 수는 솔루션(최단 경로) d: O(bd)의 깊이에서 기하급수적으로 증가하며,[22] 여기서 b는 분기 계수(상태당 평균 후계자 수)이다.이것은 목표 상태가 존재하며 시작 상태부터 도달할 수 있다고 가정합니다.목표 상태가 존재하지 않고 상태 공간이 무한할 경우 알고리즘은 종료되지 않습니다.

휴리스틱 함수는 A* 검색의 실제 성능에 큰 영향을 미칩니다. 좋은 휴리스틱을 사용하면 A*는 정보가 없는 검색이 확장되는 많은 b 노드를d 제거할 수 있기 때문입니다.그 품질은 효과적인 분기 계수 b*로 나타낼 수 있습니다.이것은 확장으로 생성된 노드 수, N 및 솔루션의 깊이를 측정하여[23] 문제 인스턴스에 대해 경험적으로 판단할 수 있습니다.

좋은 휴리스틱은 유효 분기 인자(최적값은 b* = 1)가 낮은 휴리스틱입니다.

검색 공간이 트리이고 단일 목표 상태가 있으며 휴리스틱 함수 h가 다음 조건을 만족하는 경우 시간 복잡도는 다항식입니다.

여기서* h는 x에서 목표까지의 정확한 비용인 최적의 휴리스틱입니다.즉, h의 오차는 x에서 [16][22]목표까지의 실제 거리를 반환하는 "완벽한 경험적*" h의 로그보다 빠르게 증가하지 않습니다.

A*의 공간 복잡도는 생성된 모든 노드를 [1]메모리에 보관하기 때문에 다른 모든 그래프 검색 알고리즘과 거의 동일합니다.실제로는 이것이 A* 검색의 가장 큰 단점으로 판명되어 반복 심도 A*, 메모리 한계 A* 및 SMA*와 같은 메모리 한계 휴리스틱 검색의 개발로 이어집니다.

적용들

A*는 비디오 게임 등의 응용 프로그램에서 일반적인 경로 검색 문제에 자주 사용되지만 원래는 일반적인 그래프 통과 [4]알고리즘으로 설계되었습니다.NLP에서 [24]확률적 문법을 사용한 구문 분석 문제를 포함한 다양한 문제에서 응용 프로그램을 찾는다.기타 사례로는 온라인 [25]학습이 포함된 정보 검색이 있습니다.

다른 알고리즘과의 관계

A*가 욕심 많은 베스트 퍼스트 검색 알고리즘과 다른 점은 이미 이동한 비용/거리 g(n)를 고려한다는 것입니다.

Dijkstra 알고리즘의 일부 일반적인 변형은 A*의 특수한 경우로 볼 수 있습니다. 여기서 모든 [10][11]노드에 대한 h ( ) { h ( n ) =} 、 Dijkstra 와 A* 는 모두 동적 [26]프로그래밍의 특수한 경우입니다.A* 자체는 분기 및 [27]바운드의 일반화의 특수한 경우입니다.

변종

A*는 양방향 검색 알고리즘에도 적용할 수 있습니다.정지 [31]기준에 각별한 주의가 필요합니다.

「 」를 참조해 주세요.

메모들

  1. ^ "A*-like"는 A*와 마찬가지로 시작 노드에서 시작하는 경로를 한 번에 한 에지씩 확장하여 알고리즘 검색을 의미합니다.예를 들어 목표에서 후방으로 또는 양방향으로 동시에 검색하는 알고리즘은 제외됩니다.게다가 이 정리에 포함되는 알고리즘은, A*보다 「더 많은 정보를 얻을 수 없는」 것이어야 합니다.
  2. ^ 목표 노드는 f 값이 낮은 다른 노드가 남아 있는 경우 목표에 대한 경로가 짧아질 수 있으므로 여러 번 통과될 수 있습니다.

레퍼런스

  1. ^ a b c Russell, Stuart J. (2018). Artificial intelligence a modern approach. Norvig, Peter (4th ed.). Boston: Pearson. ISBN 978-0134610993. OCLC 1021874142.
  2. ^ Delling, D.; Sanders, P.; Schultes, D.; Wagner, D. (2009). "Engineering Route Planning Algorithms". Algorithmics of Large and Complex Networks: Design, Analysis, and Simulation. Lecture Notes in Computer Science. Vol. 5515. Springer. pp. 11个$7–139. CiteSeerX 10.1.1.164.8916. doi:10.1007/978-3-642-02094-0_7. ISBN 978-3-642-02093-3.
  3. ^ Zeng, W.; Church, R. L. (2009). "Finding shortest paths on real road networks: the case for A*". International Journal of Geographical Information Science. 23 (4): 531–543. doi:10.1080/13658810801949850. S2CID 14833639.
  4. ^ a b c Hart, P. E.; Nilsson, N. J.; Raphael, B. (1968). "A Formal Basis for the Heuristic Determination of Minimum Cost Paths". IEEE Transactions on Systems Science and Cybernetics. 4 (2): 100–107. doi:10.1109/TSSC.1968.300136.
  5. ^ Doran, J. E.; Michie, D. (1966-09-20). "Experiments with the Graph Traverser program". Proc. R. Soc. Lond. A. 294 (1437): 235–259. Bibcode:1966RSPSA.294..235D. doi:10.1098/rspa.1966.0205. ISSN 0080-4630. S2CID 21698093.
  6. ^ a b Nilsson, Nils J. (2009-10-30). The Quest for Artificial Intelligence (PDF). Cambridge: Cambridge University Press. ISBN 9780521122931.
  7. ^ Edelkamp, Stefan; Jabbar, Shahid; Lluch-Lafuente, Alberto (2005). "Cost-Algebraic Heuristic Search" (PDF). Proceedings of the Twentieth National Conference on Artificial Intelligence (AAAI): 1362–1367.
  8. ^ Hart, Peter E.; Nilsson, Nils J.; Raphael, Bertram (1972-12-01). "Correction to 'A Formal Basis for the Heuristic Determination of Minimum Cost Paths'" (PDF). ACM SIGART Bulletin (37): 28–29. doi:10.1145/1056777.1056779. ISSN 0163-5719. S2CID 6386648.
  9. ^ a b Dechter, Rina; Judea Pearl (1985). "Generalized best-first search strategies and the optimality of A*". Journal of the ACM. 32 (3): 505–536. doi:10.1145/3828.3830. S2CID 2092415.
  10. ^ a b 를 클릭합니다De Smith, Michael John; Goodchild, Michael F.; Longley, Paul (2007), Geospatial Analysis: A Comprehensive Guide to Principles, Techniques and Software Tools, Troubadour Publishing Ltd, p. 344, ISBN 9781905886609.
  11. ^ a b 를 클릭합니다Hetland, Magnus Lie (2010), Python Algorithms: Mastering Basic Algorithms in the Python Language, Apress, p. 214, ISBN 9781430232377.
  12. ^ Martelli, Alberto (1977). "On the Complexity of Admissible Search Algorithms". Artificial Intelligence. 8 (1): 1–13. doi:10.1016/0004-3702(77)90002-9.
  13. ^ Felner, Ariel; Uzi Zahavi (2011). "Inconsistent heuristics in theory and practice". Artificial Intelligence. 175 (9–10): 1570–1603. doi:10.1016/j.artint.2011.02.001.
  14. ^ Zhang, Zhifu; N. R. Sturtevant (2009). Using Inconsistent Heuristics on A* Search. Twenty-First International Joint Conference on Artificial Intelligence.
  15. ^ Pohl, Ira (1970). "First results on the effect of error in heuristic search". Machine Intelligence. 5: 219–236.
  16. ^ a b Pearl, Judea (1984). Heuristics: Intelligent Search Strategies for Computer Problem Solving. Addison-Wesley. ISBN 978-0-201-05594-8.
  17. ^ Pohl, Ira (August 1973). "The avoidance of (relative) catastrophe, heuristic competence, genuine dynamic weighting and computational issues in heuristic problem solving" (PDF). Proceedings of the Third International Joint Conference on Artificial Intelligence (IJCAI-73). Vol. 3. California, USA. pp. 11–17.
  18. ^ Köll, Andreas; Hermann Kaindl (August 1992). "A new approach to dynamic weighting". Proceedings of the Tenth European Conference on Artificial Intelligence (ECAI-92). Vienna, Austria. pp. 16–17.
  19. ^ Pearl, Judea; Jin H. Kim (1982). "Studies in semi-admissible heuristics". IEEE Transactions on Pattern Analysis and Machine Intelligence. 4 (4): 392–399. doi:10.1109/TPAMI.1982.4767270. PMID 21869053. S2CID 3176931.
  20. ^ Ghallab, Malik; Dennis Allard (August 1983). "Aε – an efficient near admissible heuristic search algorithm" (PDF). Proceedings of the Eighth International Joint Conference on Artificial Intelligence (IJCAI-83). Vol. 2. Karlsruhe, Germany. pp. 789–791. Archived from the original (PDF) on 2014-08-06.
  21. ^ Reese, Bjørn (1999). AlphA*: An ε-admissible heuristic search algorithm (Report). Archived from the original on 2016-01-31. Retrieved 2014-11-05.
  22. ^ a b Russell, Stuart; Norvig, Peter (2003) [1995]. Artificial Intelligence: A Modern Approach (2nd ed.). Prentice Hall. pp. 97–104. ISBN 978-0137903955.
  23. ^ Russell, Stuart; Norvig, Peter (2009) [1995]. Artificial Intelligence: A Modern Approach (3rd ed.). Prentice Hall. p. 103. ISBN 978-0-13-604259-4.
  24. ^ Klein, Dan; Manning, Christopher D. (2003). A* parsing: fast exact Viterbi parse selection. Proc. NAACL-HLT.
  25. ^ Kagan E.; Ben-Gal I. (2014). "A Group-Testing Algorithm with Online Informational Learning" (PDF). IIE Transactions. 46 (2): 164–184. doi:10.1080/0740817X.2013.803639. S2CID 18588494.
  26. ^ Ferguson, Dave; Likhachev, Maxim; Stentz, Anthony (2005). A Guide to Heuristic-based Path Planning (PDF). Proc. ICAPS Workshop on Planning under Uncertainty for Autonomous Systems.
  27. ^ Nau, Dana S.; Kumar, Vipin; Kanal, Laveen (1984). "General branch and bound, and its relation to A∗ and AO∗" (PDF). Artificial Intelligence. 23 (1): 29–58. doi:10.1016/0004-3702(84)90004-3.
  28. ^ Hansen, Eric A., Rong Zhou."언제든지 휴리스틱 검색.Wayback Machine' J. Art에서 2016-11-05년 아카이브.인텔Res. (JAIR) 28 (2007) : 267-297.
  29. ^ Fareh, Raouf; Baziyad, Mohammed; Rahman, Mohammad H.; Rabie, Tamer; Bettayeb, Maamar (2019-05-14). "Investigating Reduced Path Planning Strategy for Differential Wheeled Mobile Robot". Robotica. 38 (2): 235–255. doi:10.1017/S0263574719000572. ISSN 0263-5747. S2CID 181849209.
  30. ^ Erasmus University Rotterdam, Econometric Institute EI 2009-10/Econometric Institute의 Pijls, Wim; Post, Henk "최단 경로를 위한 또 다른 양방향 알고리즘" 에라스무스 경제학부
  31. ^ Goldberg, Andrew V.; Harrelson, Chris; Kaplan, Haim; Werneck, Renato F. "Efficient Point-to-Point Shortest Path Algorithms" (PDF). Princeton University. Archived (PDF) from the original on 18 May 2022.

추가 정보

외부 링크