패러데이의 귀납법

Faraday's law of induction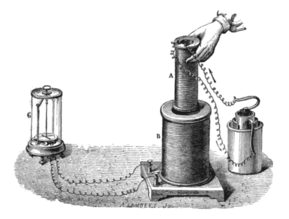
와이어 코일 사이의 유도를 보여주는 패러데이의 실험: 액체 배터리(오른쪽)는 작은 코일(A)을 통해 흐르는 전류를 제공하여 자기장을 생성합니다. 코일이 정지되어 있으면 전류가 유도되지 않습니다. 그러나 소형 코일이 대형 코일(B)을 드나들 때 대형 코일을 통한 자속이 변화하여 갈바노미터(G)에 의해 감지되는 전류를 유도합니다.[1]

패러데이의 유도 법칙(또는 간단히 패러데이의 법칙)은 전자기학의 기본 법칙으로 자기장이 전기 회로와 어떻게 상호작용하여 기전력(emf)을 발생시키는지 예측하는 법칙으로 전자기 유도라고 알려져 있습니다. 변압기, 인덕터 및 다양한 유형의 전기 모터, 발전기 및 솔레노이드의 기본 작동 원리입니다.[2][3]

맥스웰-패러데이 방정식(Maxwell-Faraday equation, 맥스웰 방정식 중 하나로 나열됨)은 공간적으로 변하는 전기장이 항상 시간에 따라 변하는 자기장을 동반한다는 사실을 설명하는 반면, 패러데이 법칙은 기전력이 있다고 말합니다. 시간에 따라 루프로 둘러싸인 표면을 통과하는 자속이 변할 때 전도성 루프에서 한 바퀴의 전도성 루프를 돌 때 단위 전하에 대해 수행되는 전자기 작업으로 정의됩니다.

패러데이의 법칙이 발견되었고 그 한 측면(트랜스포머 emf)은 나중에 맥스웰-패러데이 방정식으로 공식화되었습니다. 패러데이 법칙의 방정식은 맥스웰-패러데이 방정식(변압기 emf를 설명함)과 로런츠 힘(운동적 emf를 설명함)에 의해 유도될 수 있습니다. 맥스웰-패러데이 방정식의 적분 형태는 변압기 emf만을 설명하는 반면, 패러데이 법칙의 방정식은 변압기 emf와 운동 emf를 모두 설명합니다.

에 대한 기사
전자기학
Solenoid
정전기학
자기 정역학
전기역학
전기망
자기회로
공변 공식
사이언티스트

역사

패러데이의 철환 장치를 보여주는 다이어그램입니다. 왼쪽 코일의 변화하는 자속은 오른쪽 코일에 전류를 유도합니다.[4]

전자기 유도는 1831년 마이클 패러데이와 1832년 조셉 헨리에 의해 독립적으로 발견되었습니다.[5] 패러데이는 그의 실험 결과를 최초로 발표했습니다.[6][7] 패러데이가 전자기 유도를 처음으로 실험적으로 시연한 것(1831년 8월 29일)[8]에서 그는 철고리(토러스)의 반대쪽에 두 개의 전선을 감쌌습니다(현대의 토로이드 변압기와 비슷한 배열). 최근에 발견된 전자석의 특성에 대한 그의 평가를 바탕으로, 그는 전류가 한 전선으로 흐르기 시작할 때 일종의 파동이 고리를 통해 이동하여 반대쪽에 어떤 전기적 효과를 일으킬 것이라고 예상했습니다. 그는 한 전선을 갈바노미터에 꽂고, 다른 전선을 배터리에 연결하는 것을 지켜보았습니다. 실제로, 그는 전선을 배터리에 연결할 때 과도 전류("전기의 파동"이라고 불림)를 보았고, 분리할 때 또 다른 전류를 보았습니다.[9]: 182–183 이러한 유도는 배터리를 연결했다가 분리할 때 발생하는 자속의 변화 때문이었습니다.[4] 두 달 안에 패러데이는 전자기 유도의 다른 징후들을 몇 가지 발견했습니다. 예를 들어, 그는 전선의 코일을 빠르게 안팎으로 밀어 넣었을 때 과도 전류를 보았고, 미끄러지는 전기 리드("Faraday's disk")로 막대 자석 근처의 구리 디스크를 회전시킴으로써 정상 전류(DC)를 생성했습니다.[9]: 191–195

패러데이 디스크, 최초의 전기 발전기, 호모폴라 발전기의 일종.

마이클 패러데이는 그가 역선이라고 부르는 개념을 이용해 전자기 유도를 설명했습니다. 그러나, 그 당시의 과학자들은 그의 이론적인 아이디어들이 수학적으로 공식화되지 않았다는 이유로 널리 거절했습니다.[9]: 510 예외는 제임스 클러크 맥스웰(James Clerk Maxwell)인데, 그는 1861-62년에 패러데이의 아이디어를 그의 정량적 전자기 이론의 기초로 사용했습니다.[9]: 510 [10][11] 맥스웰의 논문에서 전자기 유도의 시변적인 측면은 올리버 헤비사이드가 패러데이 법칙의 원래 버전과는 다르지만 패러데이 법칙으로 언급한 미분방정식으로 표현되며, 운동적 emf에 대해서는 기술하지 않습니다. 헤비사이드의 버전(아래 맥스웰-패러데이 방정식 참조)은 맥스웰 방정식으로 알려진 방정식 그룹에서 오늘날 인식되는 형태입니다.

1834년 에밀 렌츠가 공식화한 [12]렌츠의 법칙은 "회로를 통한 플럭스"를 설명하고 전자기 유도로 인한 유도 기전력과 전류의 방향을 제시합니다(아래의 예에서 자세히 설명합니다).

알버트 아인슈타인에 따르면, 그의 특수 상대성 이론의 많은 기초와 발견은 1834년 패러데이에 의해 이 유도 법칙에 의해 제시되었습니다.[13][14]

패러데이 법칙

왼쪽 솔레노이드를 통해 교류 전류가 흐르며 자기장이 변화합니다. 이 필드는 전자기 유도에 의해 오른쪽 와이어 루프에 전류가 흐르게 합니다.

패러데이 법칙의 가장 일반적인 버전은 다음과 같습니다.

닫힌 경로 주위의 기전력은 경로로 둘러싸인 자속의 시간 변화율의 음수와 같습니다.[15][16]

수학문

표면 적분의 정의는 표면 σ를 작은 표면 요소로 분할하는 것에 의존합니다. 각 요소는 요소의 면적과 동일한 크기의 벡터 dA와 요소에 수직인 방향 및 (표면의 방향과 관련하여) "외부"를 가리킵니다.

자기장에 있는 와이어 루프의 경우, 자속 φ은 경계가 주어진 루프인 모든 표면 σ에 대해 정의됩니다. 와이어 루프가 움직일 수 있으므로 표면에 σ(t)라고 적습니다. 자속은 표면 적분입니다.

여기서, dA는 이동면 σ(t)의 면적 벡터의 원소이고, B는 자기장이며, B·dA는 dA를 통한 플럭스의 원소를 나타내는 벡터 도트 곱. 좀 더 시각적인 측면에서 보면, 와이어 루프를 통과하는 자속은 루프를 통과하는 자기장 선의 수에 비례합니다.

B가 변하거나, 선루프가 움직이거나 변형되거나 둘 다 변하기 때문에 플럭스가 변하면, 패러데이의 유도 법칙은 선루프가 선루프를 한 바퀴 돈 단위 전하로부터 사용할 수 있는 에너지로 정의되는 기전력을 얻는다고 말합니다.[17]: ch17 [18][19] (비록 어떤 자료들은 정의를 다르게 서술하지만, 이 표현은 특수 상대성 방정식과의 호환성을 위해 선택되었습니다.) 마찬가지로 와이어를 절단하여 단선을 만들고 리드에 전압계를 부착하여 측정하는 전압입니다.

패러데이의 법칙에 따르면 기전력은 자속의 변화율에 의해서도 주어집니다.

서 E {\은 기전력(emf)이고 φ은 자속입니다.

기전력의 방향은 렌츠의 법칙에 의해 정해집니다.

수학적 형태의 전류 유도 법칙은 1845년 프란츠 에른스트 노이만에 의해 확립되었습니다.[20]

패러데이의 법칙은 크기와 변수의 방향 사이의 관계에 대한 정보를 담고 있습니다. 그러나 방향 사이의 관계는 명시적이지 않으며 수학 공식에 숨겨져 있습니다.

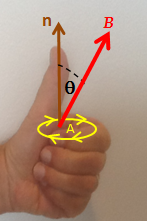
패러데이 법칙의 왼손 법칙. 플럭스의 변화인 δ φ의 부호는 왼손의 손가락으로 표현되는 자기장 B, 루프 A의 면적, 그리고 그 면적에 대한 법선 n 사이의 관계를 기반으로 합니다. δ φ가 양수일 경우 기전력의 방향은 구부러진 손가락(노란색 화살촉)의 방향과 동일합니다. δ φ가 음수이면 기전력의 방향이 화살촉을 향합니다.

렌츠의 법칙을 발동하지 않고도 패러데이의 법칙에서 직접 기전력(emf)의 방향을 알아낼 수 있습니다. 왼손 규칙을 사용하면 다음과 같이 수행할 수 있습니다.[21][22]

  • 왼손의 구부러진 손가락을 루프(노란색 선)와 정렬합니다.
  • 엄지를 펴주세요. 늘어난 엄지손가락은 n(갈색)의 방향을 나타냅니다. 이는 루프로 둘러싸인 영역의 법선입니다.
  • 플럭스의 변화인 δ φ의 부호를 구합니다. 늘어난 엄지손가락으로 표시된 대로 정상 n에 대한 초기 및 최종 플럭스(차이가 δ φ)를 결정합니다.
  • 플럭스의 변화인 δ φ가 양수이면, 구부러진 손가락은 기전력의 방향(노란색 화살촉)을 나타냅니다.
  • δ φ가 음인 경우, 기전력의 방향은 구부러진 손가락의 방향과 반대입니다(노란색 화살촉의 반대).

각각의 φ가 같은 N개의 동일한 턴으로 구성된 단단히 감긴 도선의 경우, 패러데이의 유도 법칙은 다음과 같습니다.

여기서 N은 도선의 회전수이고 φ는 단일고리를 통과하는 자속입니다.

맥스웰-패러데이 방정식

표면 σ, 경계 ∂ σ 및 오른쪽 규칙에 의해 설정된 방향 n을 갖는 켈빈-스토크스 정리의 예시.

맥스웰-패러데이 방정식은 시간에 따라 변하는 자기장은 항상 공간에 따라 변하는 비보존적인 전기장을 동반하며, 그 반대의 경우도 있다고 말합니다. 맥스웰-패러데이 방정식은

(SI 단위) 여기서 ∇ ×는 컬 연산자이고 다시 E(r, t)는 전기장이고 B(r, t)는 자기장입니다. 이러한 필드는 일반적으로 위치 r과 시간 t의 함수가 될 수 있습니다.[25]

맥스웰-패러데이 방정식은 네 개의 맥스웰 방정식 중 하나이며, 따라서 고전 전자기학 이론에서 기본적인 역할을 합니다. 켈빈-스토크스 정리에 의해 적분 형태로 쓰여질 수 있으며,[26] 따라서 패러데이의 법칙을 재현할 수 있습니다.

그림에 표시된 것처럼 σ은 닫힌 윤곽 ∂ σ에 의해 경계지어지는 표면이고, dl은 윤곽 ∂ σ의 무한소 벡터 요소이며, dA는 표면 σ의 무한소 벡터 요소입니다. 그 방향은 그 표면 패치와 직교하고 크기는 표면의 무한히 작은 패치의 면적입니다.

dl과 dA는 모두 부호 모호성을 가지고 있습니다. 올바른 부호를 얻기 위해서는 켈빈-스토크스 정리 기사에서 설명한 대로 오른쪽 규칙이 사용됩니다. 평면 표면 σ의 경우, 곡선 σ ∂의 양의 경로 요소 dl은 엄지가 표면 σ에 법선 n의 방향을 가리킬 때 오른손의 손가락으로 가리키는 것으로 오른손 규칙에 의해 정의됩니다.

∂ σ 주위에 적분하는 선을 순환이라고 합니다. E의 0이 아닌 순환은 정전기에 의해 생성된 전기장의 거동과 다릅니다. 전하 생성 E 필드는 포아송 방정식의 해인 스칼라 필드의 구배로 표현될 수 있으며 경로 적분이 0입니다. 기울기 정리를 참조하십시오.

적분 방정식은 공간을 통과하는 모든 경로 ∂ σ와 그 경로가 경계가 되는 모든 표면 σ에 대해 참입니다.

표면 σ이 시간에 따라 변하지 않으면 방정식을 다시 쓸 수 있습니다.

우측의 표면 적분은 σ를 통한 자속 φ에 대한 명시적인 표현입니다.

전체 전기장의 솔레노이드 성분인 변화하는 자속에 의해 유도되는 전기 벡터장은 부피 적분 방정식에[25]: 321 의해 비상대론적 극한에서 근사될 수 있습니다.

증명

네 개의 맥스웰 방정식(맥스웰-패러데이 방정식 포함)은 로렌츠 힘 법칙과 함께 고전 전자기학의 모든 것을 유도할 수 있는 충분한 기반입니다.[17][18] 따라서 이 방정식들을 시작으로 패러데이 법칙을 '증명'할 수 있습니다.[27][28]

시작점은 공간에서 임의의 표면 σ(이동 또는 변형 가능)을 통과하는 플럭스의 시간 도함수입니다.

(정의상) 이 총 시간 도함수는 맥스웰-패러데이 방정식과 일부 벡터 항등식의 도움으로 평가되고 단순화될 수 있습니다. 자세한 내용은 아래 상자에 있습니다.

움직이거나 변형될 수 있는 닫힌 경계(루프)를 통한 자속의 시간 도함수를 생각해 보십시오. 루프로 경계지어진 영역은 σ(t)로 표시되며, 시간 도함수는 다음과 같이 표현될 수 있습니다.

적분은 다음 두 가지 이유로 시간이 지남에 따라 변할 수 있습니다. 적분 영역이 변경되거나 통합 영역이 변경될 수 있습니다. 이렇게 선형적으로 더하면 다음과 같습니다.

여기서 t는0 임의의 정해진 시간입니다. 우변의 첫 번째 항은 변압기 emf에 해당하고, 두 번째 항은 운동성 emf에 해당한다는 것을 보여줄 것입니다(자기장에서 전도 루프의 운동 또는 변형으로 인해 전하 캐리어에 대한 자기 로렌츠 힘에서). 우변의 첫 번째 항은 맥스웰-패러데이 방정식의 적분 형식을 사용하여 다시 쓸 수 있습니다.

다음으로 우변의 두 번째 항을 분석합니다.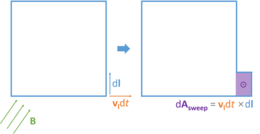

속도 v로 이동한 시간 dt에서 루프 ∂ σ의 벡터 요소 dl에 의해 휩쓸려 나가는 영역.
이것의 증명은 첫 번째 항보다 조금 더 어렵습니다. 증명에 대한 더 자세한 내용과 대안적인 접근 방법은 참고 문헌에서 찾을 수 있습니다.[27][28][29] 루프가 움직이거나 변형될 때 표면을 쓸어내립니다(오른쪽 그림 참조). 루프 dl의 작은 부분이 짧은 시간 dt 동안 속도 v로 이동함에 따라 벡터가 dA = vdt × dl인 영역을 쓸어냅니다(이 벡터는 오른쪽 그림의 디스플레이에서 바깥쪽으로 나와 있음에 유의하십시오). 따라서 시간 dt에 따른 루프의 변형이나 움직임에 의한 루프를 통한 자속의 변화는

여기에는 트리플 스칼라 제품의 ID가 사용됩니다. 그러므로,

여기서 v는 루프 σ ∂의 한 부분의 속도입니다.

이것들을 종합하면,

결과는 다음과 같습니다.

여기서 ∂ σ는 표면 σ의 경계(루프)이고 v는 경계의 일부분의 속도입니다.

전도성 루프의 경우, 기전력(emf)은 단위 전하가 루프를 한 바퀴 돌 때 하는 전자기 작업이며, 이 작업은 로렌츠 힘에 의해 수행됩니다. 따라서 emf는 다음과 같이 표현됩니다.

여기서 은 emf이고 v는 단위 충전 속도입니다.

거시적 관점에서, 고리의 한 부분에 있는 전하의 경우 v는 평균적으로 두 가지 성분으로 구성됩니다. 하나는 세그먼트 v를t 따른 전하의 속도이고, 다른 하나는 세그먼트 v의l 속도입니다(루프가 변형되거나 이동됨). v의t 방향이 방향과 같기 때문에 v는t 전하에 대한 작업에 기여하지 않습니다 수학적으로,

since is perpendicular to as and are along the same direction. 이제 우리는 전도성 고리의 경우 emf가 고리를 통과하는 자속의 시간-도함수와 같다는 것을 알 수 있습니다. 따라서 이제 우리는 (전도 루프에 대한) 패러데이 법칙의 방정식에 도달합니다.
여기서 = ∮(E + v × B) ⋅ dl {\textstyle {\mathcal {E}}=\point \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\cdot \mathrm {d} \mathbf {l}. 이 적분을 깨면, d l{\ {E} \ {d l} ∮는 ying 자기장으로 인해) 변압기 em 및 ⋅ (v ×B) ∮ = ⋅ d l {\textstyle \point \left(\mathbf {v} \times \mathbf {B} \right)\cdot \mathrm {d} \mathbf l} =\point \left(\mathbf {v}는 운동성 기전력(자기장에서 고리의 운동 또는 변형에 의한 전하의 자기 로렌츠 힘으로 인한 것)에 대한 것입니다.

예외

참고 항목: 패러데이 역설

패러데이의 법칙을 다음과 같이 일반화하고자 합니다. ∂ σ가 공간상 임의의 폐루프인 경우, σ σ을 통한 자속의 총 시간 도함수는 ∂ σ 주변의 기전력과 같습니다. 그러나 이 진술이 항상 사실인 것은 아니며, 그 이유는 전도체가 없을 때 빈 공간에서 EMF가 정의되지 않는다는 명백한 이유 때문만은 아닙니다. 앞 절에서 언급한 바와 같이 추상곡선 σ ∂의 속도가 전기를 전도하는 물질의 실제 속도와 일치하지 않는 한 패러데이의 법칙이 작동하는 것은 보장되지 않습니다. 아래에 예시된 두 가지 예는 ∂ σ의 운동이 재료의 운동과 분리될 때 종종 잘못된 결과를 얻는다는 것을 보여줍니다.

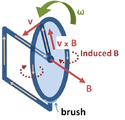
  • Faraday's homopolar generator. The disc rotates with angular rate ω, sweeping the conducting radius circularly in the static magnetic field B (which direction is along the disk surface normal). The magnetic Lorentz force v × B drives a current along the conducting radius to the conducting rim, and from there the circuit completes through the lower brush and the axle supporting the disc. This device generates an emf and a current, although the shape of the "circuit" is constant and thus the flux through the circuit does not change with time.
    패러데이의 호모폴라 발전기. 디스크는 각속도 ω으로 회전하며, (디스크 표면의 정상 방향인) 정적 자기장 B에서 원형으로 전도 반경을 쓸어냅니다. 자기 로렌츠 힘 v × B는 전도 반경을 따라 전도 림으로 전류를 구동하고, 여기서 회로는 하부 브러시와 디스크를 지지하는 액슬을 통해 완성됩니다. 이 장치는 "회로"의 모양이 일정하므로 회로를 통과하는 플럭스가 시간에 따라 변하지는 않지만 기전력과 전류를 생성합니다.
  • A wire (solid red lines) connects to two touching metal plates (silver) to form a circuit. The whole system sits in a uniform magnetic field, normal to the page. If the abstract path ∂Σ follows the primary path of current flow (marked in red), then the magnetic flux through this path changes dramatically as the plates are rotated, yet the emf is almost zero. After Feynman Lectures on Physics[17]: ch17 
    와이어(빨간색 실선)는 두 개의 접촉 금속판(은)에 연결되어 회로를 형성합니다. 전체 시스템은 페이지에 대해 정상적인 균일한 자기장에 위치합니다. 추상 경로 ∂ σ가 전류 흐름의 기본 경로를 따르는 경우(빨간색으로 표시됨), 플레이트가 회전함에 따라 이 경로를 통과하는 자속은 극적으로 변하지만 기전력은 거의 0입니다. 파인만의 물리학[17]: ch17 강의 이후

∂ σ의 경로가 물질과 같은 속도로 이동하는 것을 주의하면 이러한 예를 분석할 수 있습니다. 또는 로런츠 힘 법칙과 맥스웰-패러데이 방정식을 결합하여 항상 정확하게 emf를 계산할 수 있습니다.[17]: ch17 [31]

여기서 "(1) [vm]는 도체의 속도라는 점에 유의하는 것이 매우 중요합니다. 일반적으로 경로 요소 dl과 (2)의 속도가 아니라, 시간에 대한 편미분은 면적이 시간의 함수이기 때문에 적분 외부로 이동할 수 없습니다."[31]

패러데이의 법칙과 상대성 이론

자세한 정보: 자석 및 도체 이동 문제

두가지 현상

패러데이 법칙은 두 가지 다른 현상을 설명하는 단 하나의 방정식으로, 움직이는 전선의 자기력에 의해 발생하는 운동 기전력(로런츠 힘 참조)과 변하는 자기장에 의해 발생하는 변압기 기전력(맥스웰-패러데이 방정식에 의해 설명됨)입니다.

제임스 클러크 맥스웰은 1861년에 발표한 힘의 물리적 선에 관한 논문에서 이 사실에 주목했습니다.[32] 그 논문의 제2부 후반부에서 맥스웰은 두 현상 각각에 대해 별도의 물리적 설명을 합니다.

전자기 유도의 이 두 가지 측면에 대한 언급은 일부 현대 교과서에서 이루어졌습니다.[33] 리처드 파인먼은 다음과 같이 말합니다.

따라서 회로의 기전력이 회로를 통과하는 자속의 변화율과 같다는 "플럭스 규칙"은 플럭스가 변하는 이유가 장이 변하기 때문인지 아니면 회로가 움직이기 때문인지(또는 둘 다)에 적용됩니다.

그러나 규칙에 대한 설명에서 우리는 "회로 이동"에 대해 v × B, "현장 변화"에 대해 ∇ × E = - ∂B 두 가지 경우에 대해 완전히 다른 두 가지 법칙을 사용했습니다.

우리는 물리학에서 그렇게 단순하고 정확한 일반 원리가 두 가지 다른 현상의 관점에서 분석을 진정으로 이해하는 데 필요한 다른 곳을 알지 못합니다.

— Richard P. Feynman, The Feynman Lectures on Physics[34]

[dubious – 토론]

4차원 형식주의에 입각한 설명

일반적인 경우, 움직이는 전선이나 회로에서 전하에 대한 자기력의 작용에 의한 운동성 방출이 면적을 변화시키는 것에 대한 설명은 만족스럽지 않습니다. 사실 와이어나 회로의 전하가 완전히 없을 수도 있는데, 이 경우 전자기 유도 효과가 사라집니까? 이 상황은 전자기장의 적분 방정식을 4차원 공변 형태로 쓸 때 패러데이 법칙에서 부분 시간 도함수 대신 회로를 통한 자속의 총 시간 도함수가 나타나는 기사에서 분석됩니다. [35] 따라서 전자기 유도는 자기장이 시간에 따라 변화하거나 회로의 면적이 변화할 때 나타납니다. 물리적인 관점에서는 유도 기전력이 아니라 유도 세기 =- ∇E - ∂ A ∂ t {\textstyle \mathbf {E} =-\nmathcal {E 자속이 변할 때 회로에서 발생합니다. 경우 자기장의 변화로부터 에 대한 기여는∂A ∂ t -A}}{\t}}, 서 A \mathbf {A}는 벡터 포텐셜입니다. 일정한 자기장의 경우 회로 영역이 변화하고 있다면, 회로의 일부가 필연적으로 이동하고 있는 것입니다. 그리고 E 는 회로를 통과하는 정지 기준 프레임 K에존재하는 자기장 의 로렌츠 변환의 결과로 이동하는 기준 프레임 K'에서 회로의 이 부분에서 나타납니다. K'에 필드가 존재하는 것은 전하가 회로에 존재하는지 여부에 관계없이 이동 회로에서 유도 효과의 결과로 간주됩니다. 전도 회로에서 필드는 전하의 움직임을 유발합니다. 기준 프레임 K에서가 - ∇ E -\n 형태인 유도 의 기전력 모양입니다.회로를 따라 취한라는 는 필드를 생성하는 것 같습니다

아인슈타인의 견해

이 명백한 이분법에 대한 성찰은 알버트 아인슈타인이 특수 상대성 이론을 개발하게 한 주요 경로 중 하나였습니다.

현재 일반적으로 이해되는 맥스웰의 전기역학은 움직이는 물체에 적용될 때 현상에 고유하지 않은 것처럼 보이는 비대칭을 초래한다고 알려져 있습니다. 예를 들어, 자석과 도체의 상호 전기 동역학적 작용을 예로 들어보자.

여기서 관찰 가능한 현상은 전도체와 자석의 상대적인 운동에만 의존하는 반면, 관습적인 관점은 이 두 물체 중 하나 또는 다른 하나가 운동하고 있는 두 경우를 극명하게 구분합니다. 자석이 움직이고 있고 도체가 정지해 있는 경우, 자석 근처에 일정한 에너지를 가진 전기장이 생겨 도체의 일부가 있는 곳에서 전류를 발생시킵니다.

그러나 자석이 정지해 있고 도체가 움직이고 있다면 자석 근처에는 전기장이 발생하지 않습니다. 그러나 전도체에서 우리는 전기력을 발견하는데, 그 자체는 해당 에너지가 없지만 논의된 두 경우에서 상대 운동의 동일성을 가정할 때 발생하는 기전력은 전자의 경우와 동일한 경로와 강도의 전류에 대해 발견됩니다.

이런 종류의 예들은 "빛 매체"에 상대적인 지구의 어떤 운동도 발견하려는 성공적이지 못한 시도들과 함께, 전기 역학의 현상들과 역학은 절대 정지의 개념에 상응하는 속성들을 가지고 있지 않다는 것을 암시합니다.

— Albert Einstein, On the Electrodynamics of Moving Bodies[36]

참고 항목

참고문헌

  1. ^ Poyser, Arthur William (1892). Magnetism and Electricity: A manual for students in advanced classes. London and New York: Longmans, Green, & Co. Fig. 248, p. 245. Retrieved 2009-08-06.
  2. ^ Sadiku, M. N. O. (2007). Elements of Electromagnetics (4th ed.). New York & Oxford: Oxford University Press. p. 386. ISBN 978-0-19-530048-2.
  3. ^ "Applications of electromagnetic induction". Boston University. 1999-07-22.
  4. ^ a b Giancoli, Douglas C. (1998). Physics: Principles with Applications (5th ed.). pp. 623–624.
  5. ^ "A Brief History of Electromagnetism" (PDF).
  6. ^ Ulaby, Fawwaz (2007). Fundamentals of applied electromagnetics (5th ed.). Pearson:Prentice Hall. p. 255. ISBN 978-0-13-241326-8.
  7. ^ "Joseph Henry". Member Directory, National Academy of Sciences. Retrieved 2016-12-30.
  8. ^ Faraday, Michael; Day, P. (1999-02-01). The philosopher's tree: a selection of Michael Faraday's writings. CRC Press. p. 71. ISBN 978-0-7503-0570-9. Retrieved 28 August 2011.
  9. ^ a b c d Williams, L. Pearce (1965). Michael Faraday. New York, Basic Books.[전체 인용 필요]
  10. ^ Clerk Maxwell, James (1904). A Treatise on Electricity and Magnetism. Vol. 2 (3rd ed.). Oxford University Press. pp. 178–179, 189.
  11. ^ "Archives Biographies: Michael Faraday". The Institution of Engineering and Technology.
  12. ^ Lenz, Emil (1834). "Ueber die Bestimmung der Richtung der durch elektodynamische Vertheilung erregten galvanischen Ströme". Annalen der Physik und Chemie. 107 (31): 483–494. Bibcode:1834AnP...107..483L. doi:10.1002/andp.18341073103.
    논문의 일부 번역은 에서 이용할 수 있습니다.
  13. ^ Siegel, Ethan (1 March 2019). "Relativity Wasn't Einstein's Miracle; It Was Waiting In Plain Sight For 71 Years". Forbes. Archived from the original on 3 July 2023. Retrieved 3 July 2023.
  14. ^ Siegel, Ethan (28 June 2023). "71 years earlier, this scientist beat Einstein to relativity - Michael Faraday's 1834 law of induction was the key experiment behind the eventual discovery of relativity. Einstein admitted it himself". Big Think. Archived from the original on 28 June 2023. Retrieved 3 July 2023.
  15. ^ Jordan, Edward; Balmain, Keith G. (1968). Electromagnetic Waves and Radiating Systems (2nd ed.). Prentice-Hall. p. 100. Faraday's Law, which states that the electromotive force around a closed path is equal to the negative of the time rate of change of magnetic flux enclosed by the path.
  16. ^ Hayt, William (1989). Engineering Electromagnetics (5th ed.). McGraw-Hill. p. 312. ISBN 0-07-027406-1. The magnetic flux is that flux which passes through any and every surface whose perimeter is the closed path.
  17. ^ a b c d e f Feynman, Richard P. "The Feynman Lectures on Physics Vol. II". feynmanlectures.caltech.edu. Retrieved 2020-11-07.
  18. ^ a b Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Upper Saddle River, NJ: Prentice Hall. pp. 301–303. ISBN 0-13-805326-X.
  19. ^ Tipler; Mosca (2004). Physics for Scientists and Engineers. Macmillan. p. 795. ISBN 9780716708100.
  20. ^ Neumann, Franz Ernst (1846). "Allgemeine Gesetze der inducirten elektrischen Ströme" (PDF). Annalen der Physik. 143 (1): 31–44. Bibcode:1846AnP...143...31N. doi:10.1002/andp.18461430103. Archived from the original (PDF) on 12 March 2020.
  21. ^ a b Yehuda Salu (2014). "A Left Hand Rule for Faraday's Law". The Physics Teacher. 52 (1): 48. Bibcode:2014PhTea..52...48S. doi:10.1119/1.4849156. 비디오 설명
  22. ^ Salu, Yehuda. "Bypassing Lenz's Rule - A Left Hand Rule for Faraday's Law". www.PhysicsForArchitects.com. Archived from the original on 7 May 2020. Retrieved 30 July 2017.
  23. ^ Whelan, P. M.; Hodgeson, M. J. (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 0-7195-3382-1.
  24. ^ Nave, Carl R. "Faraday's Law". HyperPhysics. Georgia State University. Retrieved 2011-08-29.
  25. ^ a b Griffiths, David J. (2017). Introduction to Electrodynamics. 4 (Fourth ed.). Cambridge University Press. ISBN 978-1-108-42041-9. OCLC 965197645.
  26. ^ Harrington, Roger F. (2003). Introduction to electromagnetic engineering. Mineola, NY: Dover Publications. p. 56. ISBN 0-486-43241-6.
  27. ^ a b Davison, M. E. (1973). "A Simple Proof that the Lorentz Force, Law Implied Faraday's Law of Induction, when B is Time Independent". American Journal of Physics. 41 (5): 713. Bibcode:1973AmJPh..41..713D. doi:10.1119/1.1987339.
  28. ^ a b Krey; Owen (14 August 2007). Basic Theoretical Physics: A Concise Overview. Springer. p. 155. ISBN 9783540368052.
  29. ^ Simonyi, K. (1973). Theoretische Elektrotechnik (5th ed.). Berlin: VEB Deutscher Verlag der Wissenschaften. eq. 20, p. 47.
  30. ^ a b Stewart, Joseph V. Intermediate Electromagnetic Theory. p. 396. This example of Faraday's Law [the homopolar generator] makes it very clear that in the case of extended bodies care must be taken that the boundary used to determine the flux must not be stationary but must be moving with respect to the body.
  31. ^ a b Hughes, W. F.; Young, F. J. (1965). The Electromagnetodynamics of Fluid. John Wiley. Eq. (2.6–13) p. 53.
  32. ^ Clerk Maxwell, James (1861). "On physical lines of force". Philosophical Magazine. Taylor & Francis. 90: 11–23. doi:10.1080/14786431003659180. S2CID 135524562.
  33. ^ Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Upper Saddle River, NJ: Prentice Hall. pp. 301–3. ISBN 0-13-805326-X.
    이 글에서 "패러데이의 법칙"이라고 부르는 EMF와 관련된 법칙은 그리피스의 용어에서 "보편적인 플럭스 규칙"으로 언급된다는 점에 주목하십시오. 그리피스는 이 글에서 "맥스웰-패러데이 방정식"이라고 부르는 것을 언급하기 위해 "패러데이 법칙"이라는 용어를 사용합니다. 그래서 사실 교과서에서 그리피스의 진술은 "보편적인 플럭스 규칙"에 관한 것입니다.
  34. ^ 물리학에 관한 파인만 강의 제1권. II Ch. 17: 귀납법
  35. ^ Fedosin, Sergey G. (2019). "On the Covariant Representation of Integral Equations of the Electromagnetic Field". Progress in Electromagnetics Research C. 96: 109–122. arXiv:1911.11138. Bibcode:2019arXiv191111138F. doi:10.2528/PIERC19062902. S2CID 208095922.
  36. ^ Einstein, Albert. "On the Electrodynamics of Moving Bodies" (PDF).

더보기

외부 링크