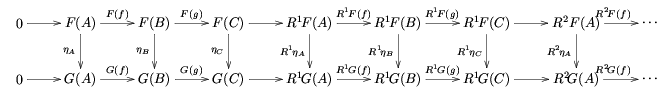파생 펑터

수학에서 특정 펑커스는 원래 펑커와 밀접하게 관련된 다른 펑커를 얻기 위해 유도될 수 있다.이 수술은 상당히 추상적이긴 하지만 수학 전체에 걸쳐 여러 가지 구조를 통합한다.

동기

여러 가지 다른 설정에서 짧은 정확한 순서가 종종 "긴 정확한 순서"를 발생시킨다고 언급되었다.파생 펑커의 개념은 이러한 관찰의 많은 부분을 설명하고 명확하게 한다.

두 아벨리아 범주 A와 B 사이에 공변량 왼쪽 정확한 functor F : A → B가 주어진다고 가정합시다.0 → A → B → C → 0이 A에서 짧은 정확 시퀀스라면 F를 적용하면 정확한 시퀀스 0 → F(A) → F(B) → F(C)를 산출할 수 있으며, 이 시퀀스를 우측으로 계속하여 긴 정확 시퀀스를 형성하는 방법을 물어볼 수 있다.엄밀히 말하면, 이 질문은 항상 주어진 정확한 순서를 오른쪽으로 이어가는 수많은 다른 방법들이 있기 때문에 잘못된 것이다.그러나 (A가 충분히 "좋다"고 한다면) F의 오른쪽 파생된 functors에 의해 주어지는 하나의 표준적인 방법이 있다는 것이 밝혀졌다.For every i≥1, there is a functor RⁱF: A → B, and the above sequence continues like so: 0 → F(A) → F(B) → F(C) → R¹F(A) → R¹F(B) → R¹F(C) → R²F(A) → R²F(B) → ... . From this we see that F is an exact functor if and only if R¹F = 0; so in a sense the right derived functors of F measure "how far" F is from being exact.

위의 짧은 정확한 순서에 있는 물체 A가 주입된 경우, 그 순서가 분할된다.분할 시퀀스에 첨가제 펑터를 적용하면 분할 시퀀스가 발생하므로, 특히 RF¹(A) = 0. 우측 유도 펑커(i>0의 경우)는 주입 시 0: 이것이 아래에 주어진 구성의 동기가 된다.

시공 및 첫 번째 특성

우리의 아벨 범주 A에 대해 우리가 만들어야 할 결정적인 가정은 충분한 주사를 가지고 있다는 것인데, 이는 A의 모든 물체 A에 대해 단형성 A → I가 존재한다는 것을 의미한다.

공변량 왼쪽-exact functor F : A → B의 오른쪽 파생 functor는 다음과 같이 정의된다.A의 객체 X로 시작하십시오.주사가 충분하기 때문에, 우리는 그 형태의 긴 정확한 순서를 만들 수 있다.

0\to X\to I^{0}\to I^{1}\to \cdots

여기서ⁱ I는 모두 주입식(이것을 X의 주입 분해능이라고 한다)이다.Functor F를 이 시퀀스에 적용하고, 첫 번째 용어를 잘라내면서, 우리는 체인 콤플렉스를 얻는다.

0\to F(I^{0})\to F(I^{1})\to \cdots

주: 이것은 일반적으로 더 이상 정확한 순서가 아니다.그러나 우리는 그것의 코호몰리를 i번째 지점에서 계산할 수 있다. (F(Iⁱ)에서 F(Iⁱ)까지의 지도 이미지에서 F(I)로; 우리는 결과 RF(Xⁱ)라고 부른다.물론 X의 주어진 주입 분해능에 따라 최종 결과가 달라지지 않고, 어떤 형태론 X → Y가 자연스럽게 형태론ⁱ RF(X) → RFⁱ(Y)를 산출하여 실제로 functor를 획득하는 등 여러 가지를 점검해야 한다.왼쪽 정확도는 0 →F(X) → F(I⁰) → F(I¹) → F(I) → F(I)가 정확하다는 것을⁰ 의미하므로 RF(X) = F(X)에 대해서만 흥미로운 것을 얻을 수 있다는 점에 유의하십시오.

(기술적으로 F의 잘 정의된 파생상품을 생산하기 위해서는 A의 모든 물체에 대한 주입 분해능을 고정해야 할 것이다.이렇게 선택한 주입 분해능은 functor RF를ⁱ 산출한다.결심에 대한 다른 선택들은 자연적으로 이형적인 functors를 산출하기 때문에 결국 선택은 별로 중요하지 않다.)

위에서 언급한 짧은 정확한 시퀀스를 긴 정확한 시퀀스로 바꾸는 특성은 뱀 보조정리 결과물이다.이것은 우리에게 파생된 펑터의 집합이 Δ-functor라는 것을 말해준다.

X 자체가 주입식이라면, 주입 분해능 0 → X → X → 0을 선택하면 모든 i i 1에 대해 RFⁱ(X) = 0을 얻을 수 있다.실제로 이 사실은 긴 정확한 시퀀스 속성과 함께 오른쪽 파생 펑터의 값을 계산하는 데 종종 사용된다.

RFⁱ(X)를 계산하는 동등한 방법은 다음과 같다: 위와 같이 X의 주입 분해능을ⁱ 취하고 K를 I→Iⁱ(i=0의 경우 I=0을^i-1 정의) 맵 I→I의^i-1 이미지가 되게 한다. 이는ⁱ I→I의ⁱ⁺¹ 커널과 같다.φ_i : I^i-1→K를ⁱ 해당 추태지도가 되도록 한다.그 다음ⁱ RF(X)는 F(φ_i)의 코커넬이다.

변형

공변량 우측외곽 Functor G로 시작하고 범주 A에 투영력이 충분하다면(즉, A의 모든 대상에는 P가 투영 객체인 경동성 P → A가 존재한다) 왼쪽에서 파생된 Functor LG를_i 유사하게 정의할 수 있다.A의 객체 X에 대해 우리는 먼저 양식의 투영적 분해능을 구성한다.

\cdots \to P_{2}\to P_{1}\to P_{0}\to 0

P가_i 투영되는 곳.우리는_i LG(X)를 얻기 위해 이 시퀀스에 G를 적용하고, 마지막 용어를 잘라내고, 호몰로지를 계산한다.이전과 마찬가지로₀ LG(X) = G(X)이다.

이 경우 정확한 긴 시퀀스는 오른쪽이 아닌 "왼쪽으로" 커진다.

A\to B\to C\to 0}

로 바뀌다

\cdots \to L_{2}G(C)\to L_{1}G(A)\to L_{1}G(B)\to L_{1}G(C)\to G(A)\to G(B)\to G(C)\to 0

.

왼쪽 파생 펑터는 모든 투영 객체에서 0이다.

하나는 또한 반대 왼쪽-exact functor F로 시작할 수 있다; 그 결과 오른쪽- 파생된 functor도 반대다.짧은 정확한 순서는

A\to B\to C\to 0}

길고 정확한 순서에 따라 달라진다.

0\to F(C)\to F(B)\to F(A)\to F(A)\to R^{1}F(B)\to R^{1}F(A)\to R^{2}F(C)\to \cdots

이러한 왼쪽 파생 펑터는 투영 시 영(0)이므로 투영 분해능을 통해 계산된다.

예

$A$ $A$ 이 $A$ (가) 아벨 범주인 경우, $A^{\{\ast \to \ast \}}$ { $A^{\{\ast \to \ast \}}$ → $A^{\{\ast \to \ast \}}$ } } $A^{\{\ast \to \ast \}}$ } {\ $displaystyle$ A $^{\\ast \to$ \ast $\}}}$ 의 형태 범주도 $A^{\{\ast \to \ast \}}$ 아벨 범주인 것이다. $\ker :A^{\{\ast \to \ast \}}\to A$ $\ker :A^{\{\ast \to \ast \}}\to A$ : $\ker :A^{\{\ast \to \ast \}}\to A$ { $\ker :A^{\{\ast \to \ast \}}\to A$ → $\ker :A^{\{\ast \to \ast \}}\to A$ → $\ker :A^{\{\ast \to \ast \}}\to A$ \ \ $\ker :A^{\{\ast \to \ast \}}\to A$ } → A ${\displaystyle \ker$ : $각각$ 의 $\ker :A^{\{\ast \to \ast \}}\to A$ 형태론을 그것의 커널에 $매핑하는$ A $^{\\{\ast \}\est$ \}\ $to A}$ 은(는) 정확하게 남겨져 있다.그것의 오른쪽 파생된 functors는

R^{i}(\ker )(f)={\begin}\case}\casegin}\ker(f)=0\\\\opername {coker}(f)&i=1\0&i>1\case}}}

Functor

\operatorname {coker}

{\

displaystyle \operatorname {coker}}이(

가) 정확하고

\operatorname {coker}

왼쪽에서 파생된 Functor는

L_{i}(\operatorname {coker})={\begin}\opername {coker}(f)&i=0\\\ker(f)=1\0&i}1\end{case}}}}

이것은 뱀 보조기구의 발현이다.

호몰로지 및 코호몰로지

셰이프 코호몰로지

$X$ $X$ 이 $X$ (가) 위상학적 공간인 경우 $,$ X {\ $displaystyle X}$ 에 있는 $Sh(X)$ 모든 아벨리아 그룹의 S $Sh(X)$ $Sh(X)$ ) ${\displaysty Sh(X)}$ 범주는 주입이 충분한 아벨리아 범주다 $X$ . $\Gamma ({\mathcal {F}}):={\mathcal {F}}(X)$ $\Gamma :Sh(X)\to Ab$ : $\Gamma :Sh(X)\to Ab$ h $\Gamma :Sh(X)\to Ab$ ( $\Gamma :Sh(X)\to Ab$ ) $\Gamma :Sh(X)\to Ab$ → 각 sheaf ${\mathcal {F}}$ ${\$ $\Gamma ({\mathcal {F}}):={\mathcal {F}}(X)$ 그룹에 ${\mathcal {F}}$ $\Gamma ({\mathcal {F}}):={\mathcal {F}}(X)$ 하는 $\Gamma :Sh(X)\to Ab$ $\Gamma :Sh(X)\to Ab$ ${\$ $displaystyle \$ $Sh($ $X)\$ $to$ $Ab}:$ $={\mathcal {F}}(X)}$ of global sections is left exact, and the right derived functors are the sheaf cohomology functors, usually written as $H^{i}(X,{\mathcal {F}})$ . Slightly more generally: if $(X,{\mathcal {O}}_{X})$ is a ringed space, then the category of all ${\mathcal {O}}_{X}$ ${\$ -modules는 ${\mathcal {O}}_{X}$ 충분한 주사를 가진 아벨리아 범주로, 글로벌 섹션 펑터의 오른쪽 파생 펑터로서 다시 피복 코호몰리를 구성할 수 있다.

이것의 특별한 경우인 코호몰로지에는 다양한 개념이 있다.

De Rham cohomology는 다지관의 국소 상수 $\mathbb {R}$ ${\$ 값 함수의 $\mathbb {R}$ 피복 공동 호몰로지다.De Rham 콤플렉스는 주입식 피복이 아니라 미세 피복에 의한 이 피복의 해결책이다.

Etale cohomology는 어떤 계획을 덮기 위한 또 다른 공동묘지 이론이다.그것은 에탈레 사이트에 있는 아벨리안 셰이브의 전지구적인 부분의 오른쪽 파생된 펑터다.

Ext functors

$R$ $R$ 이(가) 링인 $R$ 경우, $모든$ 왼쪽R {\ $displaystyle$ R} -modules의 $R$ 범주는 주입이 충분한 아벨리안 범주가 된다. $A$ $A$ 이 $A$ ( $\operatorname {Hom} (A,-):R{\text{-Mod}}\to {\mathfrak {Ab}}$ ) 고정 $좌측$ R $R$ -module인 $R$ 경우 펑터 홈 $\operatorname {Hom} (A,-):R{\text{-Mod}}\to {\mathfrak {Ab}}$ (A $\operatorname {Hom} (A,-):R{\text{-Mod}}\to {\mathfrak {Ab}}$ , $\operatorname {Hom} (A,-):R{\text{-Mod}}\to {\mathfrak {Ab}}$ - $\operatorname {Hom} (A,-):R{\text{-Mod}}\to {\mathfrak {Ab}}$ ) $\operatorname {Hom} (A,-):R{\text{-Mod}}\to {\mathfrak {Ab}}$ : $\operatorname {Hom} (A,-):R{\text{-Mod}}\to {\mathfrak {Ab}}$ $\operatorname {Hom} (A,-):R{\text{-Mod}}\to {\mathfrak {Ab}}$ → A ${\$ $R{\text{-Mod}}\to {\mathfrak {Ab}}}$ is left exact, and its right derived functors are the Ext functors $\operatorname {Ext} _{R}^{i}(A,-)$ . Alternatively $\operatorname {Ext} _{R}^{i}(-,B)$ can also be obtained as the left derived functor of the right정확한 functor $\operatorname {Hom} _{R}(-,B):R{\text{-Mod}}\to {\mathfrak {Ab}}^{op}$ $\operatorname {Hom} _{R}(-,B):R{\text{-Mod}}\to {\mathfrak {Ab}}^{op}$ $\operatorname {Hom} _{R}(-,B):R{\text{-Mod}}\to {\mathfrak {Ab}}^{op}$ ( $\operatorname {Hom} _{R}(-,B):R{\text{-Mod}}\to {\mathfrak {Ab}}^{op}$ - $\operatorname {Hom} _{R}(-,B):R{\text{-Mod}}\to {\mathfrak {Ab}}^{op}$ , $\operatorname {Hom} _{R}(-,B):R{\text{-Mod}}\to {\mathfrak {Ab}}^{op}$ ) $\operatorname {Hom} _{R}(-,B):R{\text{-Mod}}\to {\mathfrak {Ab}}^{op}$ : R $\operatorname {Hom} _{R}(-,B):R{\text{-Mod}}\to {\mathfrak {Ab}}^{op}$ → $\operatorname {Hom} _{R}(-,B):R{\text{-Mod}}\to {\mathfrak {Ab}}^{op}$ $\operatorname {Hom} _{R}(-,B):R{\text{-Mod}}\to {\mathfrak {Ab}}^{op}$ $\operatorname {Hom} _{R}(-,B):R{\text{-Mod}}\to {\mathfrak {Ab}}^{op}$ $\operatorname {Hom} _{R}(-,B):R{\text{-Mod}}\to {\mathfrak {Ab}}^{op}$ ${\$ $R{\text{-Mod}\to {\mathfrak{Ab}^{op$

다양한 개념의 코호몰로지들은 Ext functors의 특별한 경우들이며 따라서 파생된 functors의 경우도 있다.

Group cohomology is the right derived functor of the invariants functor $(-)^{G}:k[G]{\text{-Mod}}\to k[G]{\text{-Mod}}$ which is the same as $\operatorname {Hom} _{k[G]}(k,-)$ (where $k$ is the trivial $k[G]$ $k[G]$ $k[G]$ $k[G]$ $k[G]$ -module $k[G]$ ) 및 따라서 $H^{i}(G,M)=\operatorname {Ext} _{k[G]}^{i}(k,M)$ M $H^{i}(G,M)=\operatorname {Ext} _{k[G]}^{i}(k,M)$ ) $H^{i}(G,M)=\operatorname {Ext} _{k[G]}^{i}(k,M)$ = $H^{i}(G,M)=\operatorname {Ext} _{k[G]}^{i}(k,M)$ k $H^{i}(G,M)=\operatorname {Ext} _{k[G]}^{i}(k,M)$ [ $H^{i}(G,M)=\operatorname {Ext} _{k[G]}^{i}(k,M)$ $H^{i}(G,M)=\operatorname {Ext} _{k[G]}^{i}(k,M)$ i $H^{i}(G,M)=\operatorname {Ext} _{k[G]}^{i}(k,M)$ ( $H^{i}(G,M)=\operatorname {Ext} _{k[G]}^{i}(k,M)$ M ) ${\displaysty H^{i}(G,M)=\$ displaysty H^} $_{k[G]^{i,M$

Lie algebra cohomology of a Lie algebra ${\mathfrak {g}}$ over some commutative ring $k$ is the right derived functor of the invariants functor $(-)^{\mathfrak {g}}:{\mathfrak {g}}{\text{-Mod}}\to k{\text{-Mod}}$ which is the same as $\operatorname {Hom} _{U({\mathfrak {g}})}(k,-)$ $\operatorname {Hom} _{U({\mathfrak {g}})}(k,-)$ (where $k$ is again the trivial ${\mathfrak {g}}$ -module and $U({\mathfrak {g}})$ is the universal enveloping algebra of ${\mathfrak {g}$ $}}$ 그러므로 $H^{i}({\mathfrak {g}},M)=\operatorname {Ext} _{U({\mathfrak {g}})}^{i}(k,M)$ ( $H^{i}({\mathfrak {g}},M)=\operatorname {Ext} _{U({\mathfrak {g}})}^{i}(k,M)$ $H^{i}({\mathfrak {g}},M)=\operatorname {Ext} _{U({\mathfrak {g}})}^{i}(k,M)$ ) $H^{i}({\mathfrak {g}},M)=\operatorname {Ext} _{U({\mathfrak {g}})}^{i}(k,M)$ = $H^{i}({\mathfrak {g}},M)=\operatorname {Ext} _{U({\mathfrak {g}})}^{i}(k,M)$ $H^{i}({\mathfrak {g}},M)=\operatorname {Ext} _{U({\mathfrak {g}})}^{i}(k,M)$ ( $H^{i}({\mathfrak {g}},M)=\operatorname {Ext} _{U({\mathfrak {g}})}^{i}(k,M)$ ) i $H^{i}({\mathfrak {g}},M)=\operatorname {Ext} _{U({\mathfrak {g}})}^{i}(k,M)$ ⁡ $H^{i}({\mathfrak {g}},M)=\operatorname {Ext} _{U({\mathfrak {g}})}^{i}(k,M)$ ( $H^{i}({\mathfrak {g}},M)=\operatorname {Ext} _{U({\mathfrak {g}})}^{i}(k,M)$ $H^{i}({\mathfrak {g}},M)=\operatorname {Ext} _{U({\mathfrak {g}})}^{i}(k,M)$ M $H^{i}({\mathfrak {g}},M)=\operatorname {Ext} _{U({\mathfrak {g}})}^{i}(k,M)$ ) ${\displaystyle$ H $^{i}({\mathfak {g},M)=\operatorname {Ext} _{U({\mathfrak {g})}^{i}(k,M$

Hochschild cohomology of some $k$ -algebra $A$ is the right derived functor of invariants $(-)^{A}:(A,A){\text{-Bimod}}\to k{\text{-Mod}}$ mapping a bimodule $M$ to its center, also called its set of invariants $M^{A}:=Z(M):=\{m\in M\mid \forall a\in A:am=ma\}$ $M^{A}:=Z(M):=\{m\in M\mid \forall a\in A:am=ma\}$ which is the same as $\operatorname {Hom} _{A^{e}}(A,M)$ (where ${\displaystyle A^{e}:$ $=A\otimes _{k}A^{op}}$ 는 $A^{e}:=A\otimes _{k}A^{op}$ $A$ $A$ 의 포함 대수이며, $A$ ${\displaystyle$ A $}$ 은 $(A,A)$ 는 $(A,A)$ ${\displaystyle(A,A)}$ -bimodule로 $(A,A)$ 간주된다 $A$ .따라서 $HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}^{i}(A,M)$ $HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}^{i}(A,M)$ $HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}^{i}(A,M)$ ( $HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}^{i}(A,M)$ , $HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}^{i}(A,M)$ ) $HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}^{i}(A,M)$ = $HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}^{i}(A,M)$ A $HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}^{i}(A,M)$ $HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}^{i}(A,M)$ ( $HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}^{i}(A,M)$ $HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}^{i}(A,M)$ ) $HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}^{i}(A,M)$ {\ $displaystyle HH^{i}(A,M)=\operatorname {Ext} _{A^{e}}{i}(A,M$ :

토르 펑커스

왼쪽 $R$ $R$ -modules $R$ 범주에도 투영량이 충분하다.If $A$ is a fixed right $R$ -module, then the tensor product with $A$ gives a right exact covariant functor $A\otimes _{R}-:R{\text{-Mod}}\to Ab$ ; The category of modules has enough projectives so that left derived functors always가 존재한다.The left derived functors of the tensor functor are the Tor functors $\operatorname {Tor} _{i}^{R}(A,-)$ . Equivalently $\operatorname {Tor} _{i}^{R}(-,B)$ can be defined symmetrically as the left derived functors of ${\displaystyle -\otimes B$ $}$ . In fact one can combine both definitions and define $\operatorname {Tor} _{i}^{R}(-,-)$ as the left derived of $-\otimes -:{\text{Mod-}}R\times R{\text{-Mod}}\to Ab$ .

이것은 특별한 경우로서 몇가지 호몰로지 개념을 포함한다.이것은 종종 Ext functors와 코호몰로지와의 상황을 반영한다.

Group homology is the left derived of taking coinvariants $(-)_{G}:k[G]{\text{-Mod}}\to k{\text{-Mod}}$ which is the same as $k\otimes _{k[G]}-$ .

Lie algebra homology is the left derived functor of taking coinvariants ${\mathfrak {g}}{\text{-Mod}}\to k{\text{-Mod}},M\mapsto M/[{\mathfrak {g}},M]$ which is the same as $k\otimes _{U({\mathfrak {g}})}-$ .

Hochschild homology is the left derived functor of taking coinvariants $(A,A){\text{-Bimod}}\to k{\text{-Mod}},M\mapsto M/[A,M]$ which is the same as $A\otimes _{A^{e}}-$ .

왼쪽에서 파생된 개별 펑커를 선택하는 대신에 텐서 펑터의 총 파생 펑터를 취할 수도 있다.This gives rise to the derived tensor product $-\otimes ^{L}-:D({\text{Mod-}}R)\times D(R{\text{-Mod}})\to D(Ab)$ where $D$ is the derived category.

자연성

파생된 functors와 긴 정확한 시퀀스는 몇 가지 기술적 의미에서 "자연적"이다.

첫째, 양식에 대한 대응 도표를 주어라.

{\displaystyle{\begin{배열}{ccccccccc}0&, \to&A_{1}&,{\xrightarrow{f_{1}}}&B_{1}&,{\xrightarrow{g_{1}}}&C_{1}&,\to&0\\&,&\alpha \downarrow \quad&&\beta \downarrow \quad&&\gamma \downarrow \quad&&\\0&, \to&.A_{2}&,{\xrightarrow{{2f_}}}&B_{2}&,{\xrightarrow{{2g_}}}&C_{2}&,\to&0\end{배열}}}

(행들이 정확한 경우), 두 결과의 긴 정확한 순서는 통근 칸에 의해 연관된다.

둘째, η : F → G가 왼쪽 정확한 functor F에서 왼쪽 functor G로 자연적으로 변형되었다고 가정하자.그런 다음 자연변환ⁱ : : RFⁱ → RG가ⁱ 유도되며, 실제로ⁱ R은 A에서 B까지 모든 왼쪽 정확한 펑터들의 펑터 범주에서 A에서 B까지 모든 펑터 범주의 전체 펑터 범주에 이르는 펑터가 된다.더욱이 이 functor는 다음과 같은 의미에서 긴 정확한 순서와 호환된다.

0\to A{\xrightarrow {f}B{\xrightarrow {g}C\to 0

짧은 정확한 배열이고, 그 다음엔 교환 도표다.

유도된다.

이 두 가지 자연성은 모두 뱀 보조정리기가 제공하는 순서의 자연스러움에서 따온 것이다.

반대로, 파생된 functors의 특성화는ⁱ 다음과 같다: R: A → B의 functors 계열을 주어진다면, 즉, A의ⁱ 모든 주입 물체 I, R(I)=0을 모든 positive i에 대해 짧은 정확한 시퀀스를 매핑하는 것이다. 그러면 이 functors는 R의⁰ 올바른 파생된 functors이다.

일반화

파생 펑커에 대한 더 현대적이고 더 일반적인 접근법은 파생 범주의 언어를 사용한다.

1968년에 퀼렌은 모델 카테고리 이론을 개발했는데, 그것은 추상적인 범주-이론적 체계의 섬유화, 공섬유화 및 약한 동등성을 제공한다.일반적으로 약한 동등성에 대한 국소화를 통해 얻은 기본적인 호모토피 범주에 관심이 있다.Quillen 부속물은 호모토피 범주들 사이의 결합으로 이어지는 모델 범주들 사이의 결합이다.예를 들어 위상학적 공간의 범주와 단순 집합의 범주는 둘 다 신경과 실재적 결합이 사실상 호모토피 범주와 동등한 Quillen 부속물을 제공하는 Quillen 모델 구조를 인정한다.모델 구조물의 특정 물체는 "정확한 특성"(특정 형태론에 대한 리프트의 존재에 대한 고려), "Fibrant" 및 "cofibrant" 물체를 가지며, 모든 물체는 섬유질-코파이브런트 "해상도"와 약하게 동등하다.

위상학적 공간의 범주를 다루기 위해 원래 개발되었지만, 퀼렌 모델 구조는 수학의 수많은 장소에 나타난다. 특히 아벨레어 범주(위상학적 공간이나 구성표에 있는 모듈들의 모조, 모듈들의 집합 등)의 체인 복합체 범주는 그러한 형태인 약한 동등성을 가진 모델 구조를 인정한다.연쇄 살인범과 동종학 보존을 위한 연쇄 살인범 사이에 말이야종종 우리는 두 가지 모델 범주(예: 아벨리안 셰이브 콤플렉스를 아벨리안 그룹의 명백한 콤플렉스로 보내는 글로벌 섹션 펑토르) 사이에 functor를 가지고 있는데, 이는 *좋은(선한) 물체 또는 코피브란트(cofibrant)의 하위 범주 내에서 * 약한 동등성들을 보존한다.* 먼저 물체의 섬유질 또는 동위 분해능을 취한 다음 해당 functor를 적용함으로써 약한 동등성이 항상 보존되도록 전체 범주로 확장하는 데 성공했다(따라서 호모토피 범주에서 functor로 내려간다).이것은 "유래된 펑터"이다.예를 들어, 셰이프 코호몰로지(sheaf cohomology)의 "유래된 functors"는 이 파생된 functor의 출력에 대한 동어법이다.이것들을 호몰로학에 집중된 콤플렉스로 해석되는 아벨리아 그룹의 한 무리에 적용하여, 그들은 그것들의 약한 동등성을 보존하기 위한 글로벌 섹션 펑터의 실패, 그것의 "정확성"의 실패를 측정한다.모델 구조물의 일반 이론은 이 구조물의 고유성을 보여준다(섬유원 또는 동섬유원 분해능의 선택에 따라 달라지지 않는다는 것 등).

참조

Manin, Yuri Ivanovich; Gelfand, Sergei I. (2003), Methods of Homological Algebra, Berlin, New York: Springer-Verlag, ISBN 978-3-540-43583-9
Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.

Search