Ext functor
Ext functor수학에서 Ext functors는 Hom functor의 파생된 functor이다.토르 펑터와 함께 엑스는 호몰로지 대수학의 핵심 개념 중 하나로, 대수적 위상에서 나온 사상이 대수적 구조의 불변수를 정의하는데 사용된다.집단의 코호몰로지, 리 알헤브라스, 연상 알헤브라는 모두 엑스트라는 용어로 정의될 수 있다.그 이름은 첫 번째 Ext 그룹1 Ext가 한 모듈의 확장을 다른 모듈로 분류한다는 사실에서 유래되었다.
아벨 그룹들의 특수한 경우, 엑트는 라인홀드 바어(1934년)에 의해 소개되었다.사무엘 아일렌베르크와 손더스 맥레인(1942)이 이름을 지어 위상(코호몰로지 범용계수 정리)에 적용했다.어떤 링 위에 있는 모듈들에 대해 엑스는 1956년 책 Homological Algebra에서 Henri Cartan과 Eilenberg에 의해 정의되었다.[1]
정의
R을 링으로 하고 R-모드를 R에 대한 모듈의 범주로 삼아라. (좌측 R-모듈 또는 우측 R-모듈을 의미하기 위해 이것을 취할 수 있다.)고정 R-모듈 A의 경우, R-모드의 B에 대해 T(B) = HomR(A, B)을 허용한다. (여기 HomR(A, B)은 A에서 B까지의 R-선형 지도의 아벨 그룹이다. R이 동일하다면 이것은 R-모듈이다.)이것은 R-Mod에서 아벨리아 그룹 Ab의 범주에 이르는 왼쪽 정확한 functor로 오른쪽 파생 functor RT를i 가지고 있다.Ext 그룹은 에 의해 정의된 아벨 그룹이다.
정수 i의 경우정의에 따르면, 이 방법은 다음과 같다: 모든 주입 분해능을 취한다.
용어 B를 제거하고 코체인 콤플렉스를 형성한다.
각 정수 i에 대해 Exti
R(A, B)는 위치 i에서 이 콤플렉스의 코호몰로지다.그것은 내가 부정적으로 생각할 때 0이다.예를 들어 Ext0
R(A, B)는 지도 HomR(A0, I) → HomR(A, B)의 커널로, HomR(A, B1)과 이형이다.
대체 정의는 고정 R-모듈 B에 대해 Functor G(A)=HomR(A, B)을 사용한다.이것은 반대편 범주(R-Mod)op에서 Ab까지 왼쪽 정확한 펑터로 볼 수 있는 반전형 펑터다.Ext 그룹은 오른쪽 파생 펑터 RG로i 정의된다.
즉, 투사적 해상도를 선택하십시오.
A라는 용어를 제거하고 코체인 콤플렉스를 형성한다.
그러면 Exti
R(A, B)는 위치 i에서 이 콤플렉스의 코호몰로지 이다.
Cartan과 Eilenberg는 이러한 구성들이 투영적 또는 주입적 분해능의 선택과 무관하며, 두 구성 모두 동일한 Ext 그룹을 산출한다는 것을 보여주었다.[2]더욱이 고정 링 R의 경우 Ext는 각 변수(A에서는 대조, B에서는 공변량)의 펑터(functor)이다.
정류 링 R과 R-모듈 A와 B의 경우, Exti
R(A, B)는 R-모듈(이 경우R 홈(A, B)이 R-모듈이라는 것을 사용)이다.비전속 링 R의 경우, 엑스트i
R(A, B)는 일반적으로 아벨 그룹일 뿐이다.만약 R이 링 S에 대한 대수라면(특히 S가 정류적이라는 것을 의미), 엑스트i
R(A, B)는 적어도 S-모듈이다.
Ext의 속성
다음은 Ext 그룹의 기본 속성 및 계산 중 몇 가지 입니다.[3]
- 모든 R-모듈 A 및 B에 대한 Ext0
R(A, B) ≅ HomR(A, B)
- 대화 내용에는 다음 사항도 포함되어 있다.
- 만약1
R Ext(A, B)가 모든 B에 대해 0이면, A는 투영적이다(따라서 Exti
R(A, B)는 모든 i > 0에 대해 0). - 만약1
R Ext(A, B)가 모든 A에 대해 0이면, B는 주입형(따라서i
R Ext(A, B)는 모든 i > 0에 대해 0이다.
- 만약1
- , B)= 모든 i ≥ 2 및 모든 아벨리아 그룹 A와 B에 대해.[4]
- 만약 R이 정류 링이고 u in R이 0 divisor가 아니라면,
- 모든 R-모듈 B에 대해.여기서 B[u]는 B의 u-torsion 부분군, {x ∈ B: ux = 0}을 나타낸다.R을 링 의 정수로 취하면, 이 계산을 사용하여 정밀하게 생성된 아벨 그룹 A의 Z (, B) ^1}{을 계산할 수 있다.
- 앞의 예를 일반화하면, 첫 번째 모듈이 코즐 콤플렉스를 사용하여 어떤 규칙적인 시퀀스에 의한 정류 링의 몫일 때 Ext 그룹을 계산할 수 있다.[5]예를 들어, R이 필드 k에 대한 다항식 링 k[x1,...,xn]인 경우 Ext*
R(k,k)는 Ext의1 n개 생성기에서 외부 대수 S over k이다.게다가 Ext*
S(k,k)는 다항 링 R이며, 이는 Koszul 이중성의 예다.
- 파생 펑터의 일반적인 특성에 의해 Ext에 대한 두 가지 기본적인 정확한 시퀀스가 있다.[6]첫째, R-모듈의 짧은 정확한 시퀀스 0 → K → L → M → 0은 폼의 긴 정확한 시퀀스를 유도한다.
- 모든 R-모듈 A를 위해또한 0 → K → L → M → 0의 짧은 정확한 순서는 폼의 긴 정확한 순서를 유도한다.
- 모든 R-모듈 B에 대해.
- A를 정류형 노메트리안 링 R 위에 정밀하게 생성된 모듈로 두십시오.Ext는 R의 모든 승법적으로 닫힌 세트 S, 모든 R-모듈 B, 그리고 모든 정수 i에 대해 로컬리제이션으로 통한다.[8]
Ext 및 확장
연장의 등가
Ext 그룹은 모듈의 확장에 대한 그들의 관계에서 그들의 이름을 따왔다.R-모듈 A와 B를 고려할 때, A by B의 확장은 R-모듈의 짧은 정확한 시퀀스다.
두 개의 확장자
(A by B의 확장으로서) 만약 역행도가 있다면, 등가라고 한다.
5개의 보조정리법은 가운데 화살표가 이형화라는 것을 암시한다는 점에 유의한다.A by B의 연장은 사소한 연장과 같은 경우 분할이라고 한다.
A by B에 의한 확장자의 동등성 등급과1
R Ext(A, B)의 요소 사이에는 일대일 일치성이 있다.[9]사소한 확장은 Ext1
R(A, B)의 제로 요소에 해당한다.
Baer 확장자 합계
Baer sum은 Ext1
R(A, B)에 있는 아벨 그룹 구조에 대한 명시적인 설명으로, A에 의한 B에 의한 확장의 동등성 등급 집합으로 간주된다.[10]즉, 두 개의 확장자를 지정함
그리고
A 위에 풀백을 형성하십시오
E와 E의 Baer 합은 확장이다.
where the first map is and the second is .
확장의 등가성까지, Baer sum은 유사하며, 사소한 확장자를 ID 요소로 가지고 있다.연장 0 → B → E → A → 0의 음은 동일 모듈 E를 포함하는 확장이지만 동형성 B → E는 음성으로 대체된다.
아벨 범주 내 Ext 건설
요네다 노부오는 아벨 범주 C에 있는 물체 A와 B에 대한 아벨 그룹 Extn
C(A, B)를 정의했다. 이는 C가 투사량이 충분하거나 주입량이 충분할 경우 결의안의 정의와 일치한다.첫째, Ext0
C(A,B) = HomC(A, B)다음으로 Ext1
C(A, B)는 Baer sum 아래에 아벨 그룹을 형성하며, A by B에 의한 확장의 등가 등급 집합이다.마지막으로, 상위 Ext 그룹 Extn
C(A, B)는 정확한 시퀀스인 n-extension의 동등성 클래스로 정의된다.
두 확장자를 식별하는 관계에서 생성된 동등성 관계에서
{1, 2, ..., 의 모든 m에 대해 X → m {\displaystyle X_{이 존재하여 모든 결과 제곱이 통근되는 경우, 즉 A와 B에 있는 정체성인 체인 맵 → → ξ이 있는 경우.
The Baer sum of two n-extensions as above is formed by letting be the pullback of and over A, and be the pushout of and e 는 B 밑이다.[11]그러면 확장자의 Baer 합은
파생 카테고리 및 요네다 제품
중요한 점은 아벨 범주 C의 Ext 그룹은 파생 범주 D(C)인 C와 연관된 범주에서 형태론의 집합으로 볼 수 있다는 것이다.[12]파생 범주의 대상은 C에 있는 개체의 복합체다.구체적으로 말하자면
여기서 C의 물체는 0도에 집중된 복합체로 간주되며, [i]는 복합 i를 왼쪽으로 이동시키는 것을 의미한다.이 해석에서, 때때로 요네다 제품이라고 불리는 이린라인 맵이 있다.
단순히 파생된 범주에 있는 형태론의 구성이다.
요네다 제품도 좀 더 기초적인 용어로 설명할 수 있다.i = j = 0의 경우 제품은 범주 C에 있는 맵의 구성이다.일반적으로 제품은 두 개의 요네다 익스텐션을 함께 스플라이싱하여 정의할 수 있다.
대안으로 요네다 제품은 해상도 측면에서 정의될 수 있다.(이것은 파생 범주의 정의에 가깝다.)예를 들어 R-모듈 A, B, C와 함께 R을 링으로 하고 P, Q, T를 A, B, C의 투영적 해상도로 한다.Exti
R(A,B)는 체인 맵 P → Q[i]의 체인 호모토피 클래스 그룹으로 식별할 수 있다.요네다 제품은 체인 맵을 구성하여 다음과 같이 제공된다.
이 해석들 중 어느 것에 의해서도 요네다 제품은 연관성이 있다.그 결과 R∗ (, A){\는 모든 R-모듈 A에 대해 등급이 매겨진 링이다.For example, this gives the ring structure on group cohomology since this can be viewed as . Also by associativity of the Yoneda product: for any R-modules A and B, is a module over .
중요특례
- Group cohomology is defined by , where G is a group, M is a representation of G over the integers, and is the group ring of G.
- 필드 k와 A-bimodule M에 대한 대수 A의 경우 Hochschild cohomology는 다음과 같이 정의된다.
- Lie algebra cohomology is defined by , where is a Lie algebra over a commutative ring k, M is a -module, a U 는 범용 봉합 대수학이다.
- 위상학적 공간 X의 경우, sheaf cohomology는 ( ) = (X ,) . H)로 정의할 수 있다여기서 Ext는 X에 있는 아벨 그룹 셰브의 아벨리안 범주에서 취하며, X 은(는) 상수Z {\ \-값 함수의 모음입니다.
- For a commutative Noetherian local ring R with residue field k, is the universal enveloping algebra of a graded Lie algebra π*(R) over k, known as the homotopy Lie algebra of R. (To be precise, when k has characteristic 2, π*(R) has to be viewed as an "adjusted Lie대수").[13]안드레-퀼렌 코호몰로지 D*(k/R,k)부터 π*(R)까지 등급이 매겨진 리알헤브라의 자연 동형성이 있는데, k가 특성 0을 갖는다면 이형성이다.[14]
참고 항목
메모들
- ^ Weibel(1999), Cartan & Eilenberg(1956), 섹션 VI.1.
- ^ Weibel(1994), 섹션 2.4 및 2.5, 정리 2.7.6.
- ^ 와이벨(1994), 제2장, 제3장.
- ^ Weibeil(1994), Leemma 3.3.1.
- ^ Weibel(1994), 섹션 4.5.
- ^ Weibel(1994), Definition 2.1.1.
- ^ Weibel(1994), 발의안 3.3.4.
- ^ Weibel(1994), Leemma 3.3.8.
- ^ Weibel(1994), Organization 3.4.3.
- ^ Weibel(1994), Corollary 3.4.5.
- ^ 바이벨(1994), 비스트 3.4.6.약간의 사소한 수정은 에라타에 있다.
- ^ Weibel(1994), 섹션 10.4와 10.7; Gelfand & Manin(2003), 3장.
- ^ 쇠딘(1980), 표기법 14.
- ^ Avramov(2010), 섹션 10.2.
참조
- Avramov, Luchezar (2010), "Infinite free resolutions", Six lectures on commutative algebra, Birkhäuser, pp. 1–108, doi:10.1007/978-3-0346-0329-4_1, ISBN 978-3-7643-5951-5, MR 2641236
- Baer, Reinhold (1934), "Erweiterung von Gruppen und ihren Isomorphismen", Mathematische Zeitschrift, 38 (1): 375–416, doi:10.1007/BF01170643, Zbl 0009.01101
- Cartan, Henri; Eilenberg, Samuel (1999) [1956], Homological algebra, Princeton: Princeton University Press, ISBN 0-691-04991-2, MR 0077480
- Eilenberg, Samuel; MacLane, Saunders (1942), "Group extensions and homology", Annals of Mathematics, 43 (4): 757–931, doi:10.2307/1968966, JSTOR 1968966, MR 0007108
- Gelfand, Sergei I.; Manin, Yuri Ivanovich (2003), Methods of homological algebra, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-662-12492-5, ISBN 978-3-540-43583-9, MR 1950475
- Sjödin, Gunnar (1980), "Hopf algebras and derivations", Journal of Algebra, 64: 218–229, doi:10.1016/0021-8693(80)90143-X, MR 0575792
- Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.
- Weibel, Charles A. (1999), "History of homological algebra" (PDF), History of topology, Amsterdam: North-Holland, pp. 797–836, ISBN 9780444823755, MR 1721123







![{\displaystyle \operatorname {Ext} _{R}^{i}(R/(u),B)\cong {\begin{cases}B[u]&i=0\\B/uB&i=1\\0&{\text{otherwise,}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d29b19b92e3188770f876e89fe5d69f61f2bb030)
 정수로 취하면, 이 계산을 사용하여
정수로 취하면, 이 계산을 사용하여 







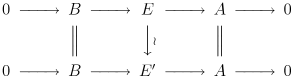

![{\displaystyle 0\to B{\xrightarrow[{f}]{}}E{\xrightarrow[{g}]{}}A\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99b91ef9769c22705bb158052b57276636e7906c)
![{\displaystyle 0\to B{\xrightarrow[{f'}]{}}E'{\xrightarrow[{g'}]{}}A\to 0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3c3b1f07bd8dcc1d933bb0a1b72b397a6e885e9)




![b\mapsto [(f(b),0)]=[(0,f'(b))]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee75b87481bf9de19754e30ff4b98f9e3a93c53f)









 B 밑이다.
B 밑이다.
![{\displaystyle \operatorname {Ext} _{\mathbf {C} }^{i}(A,B)=\operatorname {Hom} _{D({\mathbf {C} })}(A,B[i]),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd4f0a89006dc8d51c99160bf062be7b92891c2f)

![{\displaystyle P\to Q[i]\to T[i+j].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e1db5574c44feacd2e3448b888bb92c98bb8c17)
 .For example, this gives the ring structure on
.For example, this gives the ring structure on 
![{\displaystyle \operatorname {Ext} _{\mathbb {Z} [G]}^{*}(\mathbb {Z} ,\mathbb {Z} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caa2d03e117e399c9fc5a96b1e4383be50277a2b)

![{\displaystyle H^{*}(G,M)=\operatorname {Ext} _{\mathbb {Z} [G]}^{*}(\mathbb {Z} ,M)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75ea5c28b67c0bc2f3dea33b55aa97d33977f830)
![{\displaystyle \mathbb {Z} [G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f40260c366fc309a5872899d2ea34cf094855857)









