선형 분류기

기계학습 분야에서 통계적 분류의 목적은 객체의 특성을 사용하여 객체가 속한 클래스(또는 그룹)를 식별하는 것이다.선형분류기는 특성들의 선형결합 값에 기초하여 분류판정을 함으로써 이를 실현한다.객체의 특성은 특징값이라고도 하며 일반적으로 특징 벡터라고 불리는 벡터로 기계에 표시됩니다.이러한 분류기는 문서 분류와 같은 실제 문제, 더 일반적으로 많은 변수(특징)가 있는 문제에 잘 작동하여 비선형 분류기에 필적하는 정확도 수준에 도달하는 동시에 교육 및 ^[1]사용에 소요되는 시간을 단축합니다.

정의.

분류기에 대한 입력 피쳐 벡터가 실제 $벡터{\displaystyle \stackrel{}{}}$ x $→$ {\$displaystyle {x$인 경우 출력 점수는 다음과 같습니다.

${\displaystyle y=fvec {w}}\cdot {vec {x}=f\left(\sum _{j}w_{j}x_{j}\right)}}$

$여기$서 w $→$ {\$displaystyle {w}}$은 가중치의 실제 벡터이고 f는 두 벡터의 도트 곱을 원하는 출력으로 변환하는 함수입니다.(즉, w ${\displaystyle \stackrel{}{\to }}$ {\$display {w}}$은(는) 단일 형식$$또는 선형 $함수$ 매핑 x → {\displaystyle {$x}}$을(를) R에 $매핑하는{\displaystyle \stackrel{}{}}$ $것$입니다.)무게 $벡터{\displaystyle \stackrel{}{}}$ w $→$ {{$displaystyle {w}}}$은(는) 레이블이 지정된 교육 샘플 세트에서 학습됩니다.Often f is a threshold function, which maps all values of ${\displaystyle {\vec {w}}\cdot {\vec {x}}}$ above a certain threshold to the first class and all other values to the second class; e.g.,

${\displaystyle f(\mathbf {x})=param{case}1&{\text{if}}\mathbf {w}^{T}\cdot \mathbf {x}>\theta,\0&{\text{x}\end{cases}}}}}$

위첨자 T는 전치임을 나타내고$$\$displaystyle \theta는$$$스칼라 임계값을 나타냅니다.f가 더 복잡할수록 항목이 특정 클래스에 속할 확률이 높아질 수 있습니다.

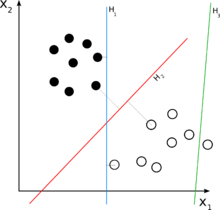
2 클래스 분류 문제의 경우 선형 분류기의 동작을 하이퍼플레인으로 고차원 입력 공간을 분할하는 것으로 시각화할 수 있습니다. 하이퍼플레인의 한쪽에 있는 모든 점은 "예"로 분류되고 다른 점은 "아니오"로 분류됩니다.

선형 분류기는 특히 x ${\displaystyle \stackrel{}{\to }}$ {\$displaystyle {x}}$이$($가) 희박한 $경우{\displaystyle \stackrel{}{}}$ 가장 빠른 분류기이기 때문에 분류 속도가 문제가 되는 상황에서 자주 사용됩니다.또한 선형 분류기는 문서 분류에서와 같이 x → {\displaystyle {$x}}$의 치수 수가 클 때 매우 잘 작동합니다. 여기서 x $→$ {\$displaystyle$ {$x}}$의 각 요소는 일반적으로 문서에서 단어 발생 횟수입니다(문서 용어 매트릭스 참조).이러한 경우 분류기는 잘 정규화되어야 합니다.

생성 모형 대 차별 모형

선형 $분류기{\displaystyle \stackrel{}{}}$ w $→$ {\$displaystyle${\$vec$ {$w$의 파라미터를 결정하는 방법에는 두 가지 종류가 있습니다.이들은 생성적이고 차별적인 ^[2][3]모델일 수 있습니다.전자의 모형 관절 확률 분포 방법, 후자의 모형 조건부 밀도 $함수{\displaystyle }$P ( ${\displaystyle c\mathrm{}}$ ${\displaystyle \mathrm{l}}$ ${\displaystyle \mathrm{a}}$ ${\displaystyle s\stackrel{}{}}$ ${\displaystyle \mathrm{x}}$ ${\displaystyle \to }$) {$displaystyle$ P$({\rm {class}}$ {$vec {x$ 방법. 이러한 알고리즘의 예는 다음과 같다.

• 선형 판별 분석(LDA)—가우스 조건부 밀도 모델을 가정합니다.
• 다항식 또는 다변량 베르누이 사건 모델이 있는 Naigive Bayes 분류기.

두 번째 방법 집합에는 교육 집합에서 출력의 품질을 최대화하려는 차별적 모델이 포함됩니다.교육 비용 함수의 추가 용어를 사용하면 최종 모델의 정규화를 쉽게 수행할 수 있습니다.선형 분류기의 차별적 훈련의 예는 다음과 같다.

• 로지스틱 회귀—감시된 훈련 세트가 분류기의 출력에 의존하는 이항 모델에 의해 생성되었다고 가정할 때 w $→$ {\$displaystyle {w}}$의 최대우도 추정.
• Perceptron: 트레이닝 세트에서 발생한 모든 오류를 수정하는 알고리즘
• Fisher의 선형 판별 분석—다른 가정 없이 클래스 간 산란 대 클래스 내 산란 비율을 최대화하는 알고리즘("LDA"와 다름)입니다.이는 본질적으로 이진수 분류를 위한 차원 축소 방법입니다.^[4]
• 서포트 벡터 머신: 의사결정 하이퍼플레인과 트레이닝 세트의 예시 사이의 마진을 최대화하는 알고리즘.

참고: 이름에도 불구하고, LDA는 이 분류법에서 차별적 모델의 클래스에 속하지 않습니다.단, LDA를 다른 주요 선형 차원 축소 알고리즘인 주성분 분석(PCA)과 비교할 때 그 이름은 의미가 있습니다.LDA는 데이터의 라벨을 사용하는 지도 학습 알고리즘이며, PCA는 라벨을 무시하는 비지도 학습 알고리즘이다.요약하자면, 이 이름은 기록 ^{[5]: 117} 아티팩트입니다.

차별적 훈련은 종종 조건부 밀도^{[citation needed]} 함수를 모델링하는 것보다 더 높은 정확도를 산출합니다.그러나 조건부 밀도^{[citation needed]} 모형을 사용하면 결측 데이터를 더 쉽게 처리할 수 있습니다.

위의 모든 선형 분류기 알고리즘은 커널 트릭을 사용하여 다른 입력 $공간{\displaystyle }$ ${\displaystyle (}$ ( ${\displaystyle x\stackrel{}{}}$ ${\displaystyle \to }$ )$$\ $displaystyle \varphi$ ( \ $vec${ $x$}$$)에서 작동하는 비선형 알고리즘으로 변환할 수 있습니다.

차별적 교육

선형 분류기의 차별적 훈련은 보통 바람직한 출력과 함께 훈련 세트가 주어지는 최적화 알고리즘과 분류기의 출력과 원하는 출력 사이의 불일치를 측정하는 손실 함수를 통해 감독된 방식으로 진행된다.따라서, 학습 알고리즘은 형태의^[1] 최적화 문제를 해결한다.

${\displaystyle {\mathbf {w}{\mathbf {w}}\R(\mathbf {w})+C\sum _{i=1}^{N}L(y_{i},\mathbf {w})^{\mathbf {x}_i}$

어디에

• w는 분류자 파라미터의 벡터입니다.
• L(y_i, wx^T_i)는 분류기의 예측과 i'th 훈련 예제의 실제 출력_i y 사이의 불일치를 측정하는 손실 함수이다.
• R(w)는 파라미터가 너무 커지는 것을 방지하는 정규화 함수입니다(과잉의 원인이 됩니다).
• C는 정규화와 손실 함수 간의 균형을 제어하는 스칼라 상수(학습 알고리즘 사용자에 의해 설정됨)입니다.

일반적인 손실 함수로는 힌지 손실(선형 SVM의 경우)과 로그 손실(선형 로지스틱 회귀 분석의 경우)이 있습니다.정규화 함수 R이 볼록한 경우 위의 문제는 볼록한 문제입니다.^[1]이러한 문제를 해결하기 위해 많은 알고리즘이 존재한다. 선형 분류에 널리 사용되는 알고리즘은 (스톡스틱) 구배 강하, L-BFGS, 좌표 강하 및 뉴턴 방법을 포함한다.

「 」를 참조해 주세요.

• 역전파
• 선형 회귀
• 퍼셉트론
• 이차 분류기
• 서포트 벡터 머신
• Winnow (알고리즘)

메모들

추가 정보

1. Y. Yang, X. Liu, "텍스트 분류 재검토", Proc.ACM SIGIR 회의, 42-49페이지, (1999)paper @ citeser
2. R. Herbrich, "커널 분류자 학습:이론과 알고리즘," MIT Press, (2001)ISBN 0-262-08306-X