라소(통계)

통계학 및 기계학습에서 라소(최소 절대수축 및 선택 연산자, 또한 Lasso 또는 LASSO)는 결과 통계모델의 예측 정확도와 해석가능성을 높이기 위해 변수 선택과 정규화를 모두 수행하는 회귀분석 방법이다.원래 지구물리학에서 도입되었고,^[1] 후에 로버트 티비시라니(^[2]Robert Tibshirani)가 이 용어를 만들었다.

라소는 원래 선형 회귀 모델을 위해 제조되었다.이 간단한 사례는 추정기에 대한 상당한 양을 보여준다.여기에는 능선 회귀 분석과 최상의 부분 집합 선택과의 관계, 라소 계수 추정치와 소위 소프트 임계값 설정 사이의 연결이 포함된다.또한 (표준 선형 회귀와 마찬가지로) 공변량이 공변량일 경우 계수 추정치가 고유할 필요는 없다는 것을 보여준다.

선형 회귀 분석을 위해 원래 정의되었지만 라소 정규화는 일반화된 선형 모형, 일반화된 추정 방정식, 비례 위험 모델 및 M-추정자를 포함한 다른 통계적 모델로 쉽게 확장된다.^[2][3]부분집합 선택을 수행하는 라소의 능력은 제약조건의 형태에 의존하며 기하학, 베이지안 통계학, 볼록 분석 등 다양한 해석을 가지고 있다.

LASSO는 기본 추구 디노잉과 밀접한 관련이 있다.

동기

Rasso는 회귀 모형의 예측 정확도와 해석 가능성을 개선하기 위해 도입되었다.모형에 사용할 알려진 공변량의 축소 집합을 선택한다.^[2][1]

역사

라소는 계수의 적합과 벌칙 모두에 대해 ${\displaystyle {for\mathrm{}}^{}}$ 1${\$} 벌칙을$$ 사용한 이전 작업을 바탕으로 1986년 지구물리학 문헌에서 독자적으로 개발되었다.통계학자 로버트 티비시라니(Robert Tibshirani)가 독자적으로 재발견하여 1996년 브레이만의 비부정적인 가사를 바탕으로 대중화하였다.^[1][4]

라소 이전에는 공변량을 선택하는 데 가장 널리 사용되는 방법이 단계적 선택이었다.그러한 접근법은 단지 소수의 공변량만이 결과와 강한 관계를 가질 때와 같은 특정한 경우에 예측 정확도를 개선할 뿐이다.그러나 다른 경우에는 예측오차를 증가시킬 수 있다.

당시 예측 정확도를 높이기 위해 가장 많이 사용된 기법은 능선 회귀였다.능선 회귀 분석은 과도한 적합성을 줄이기 위해 회귀 계수의 제곱 합계를 고정 값보다 작게 축소하여 예측 오차를 개선하지만 공변량 선택을 수행하지 않으므로 모형을 더 해석할 수 있게 만드는 데 도움이 되지 않는다.

라소는 회귀계수의 절대값 합계가 고정값보다 작도록 강요함으로써 이러한 두 가지 목표를 달성하는데, 이는 특정 계수를 0으로 강제하며, 이들 계수는 예측에 영향을 미치지 않는다.이 아이디어는 계수의 크기를 축소하는 능선 회귀 분석과 유사하지만, 능선 회귀 분석은 계수를 0으로 설정하는 경향이 있다.

기본형식

최소 제곱

각각 p 공변량과 단일 결과물로 구성된 N개의 사례로 구성된 표본을 고려하십시오.${\displaystyle y_{}}$ ${\$가 결과가 되게$$ 하고 $x{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle :=}$( ${\displaystyle {x\mathrm{}}_{}}$ ${\displaystyle {}_{}}$,${\displaystyle {}_{}{x\mathrm{}}_{}}$ 2${\displaystyle {}_{}}$,${\displaystyle }$… ,${\displaystyle {}_{}{}_p^{}}$ ) ${\displaystyle {}_{}^{}}$ ${\$i}{i}}}}}{}}}}}}}}}}}}}}}{{{}}}}}}}}}}}}}}}}}}}}}}}}}$T}}$는 i 케이스의 공변 벡터가 된다$$.그렇다면 라소의 목적은 해결하는 것이다.

${\displaystyle \min _{\beta _{0}\beta _{0}\beta _{0}-\beta _{0}-x_{i}^{T}\beta )^{2}\right\}{\text{{}{}}}}}}{{j=1}^{p} \beta _{j} \leq t.}$^[2]

Here ${\displaystyle \beta _{0}}$ is the constant coefficient, ${\displaystyle \beta :=(\beta _{1},\beta _{2},\ldots ,\beta _{p})}$ is the coefficient vector, and ${\displaystyle t}$ is a prespecified free parameter that determines the degree of regularization.

$X{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j_{}}$=${\displaystyle }$( ${\displaystyle {}_{}}$ ${\displaystyle i_{}{}_{}}$) ${\displaystyle j_{}}$ ${\$가 되도록 X ${\displaystyle$ X$}$을(를) 공변량 행렬로$$ 지정$_{j}}$ 및$$ ${\displaystyle {}_{}^{}}$ I ${\$ 스타일 $x_{i}^$${T}$은(는) $X{\displaystyle }$ ${\displaystyle X}$의 i행으로$,$ 표현은 다음과 같이 더욱 간결하게 쓸 수 있다.

${\displaystyle \min _{0}\beta _{0}\왼쪽\{\\\beta _{0}-X\beta \right\_{2}^{2}\right\}{\text{}}}}}}}}}}의 적용을 받는다.$

여기서 $\Vert {\displaystyle }$ ${\displaystyle u}$ ${\displaystyle {}_{}}$ ${\displaystyle p_{}}$= (${\displaystyle {\sum \underset{}{\overset{}{}}}^{}}$ ${\displaystyle {\underset{}{\overset{}{i}}}^{}}$= 1 ${\displaystyle {\underset{}{\overset{}{}}}^{}}$ ${\displaystyle {u\underset{}{\overset{}{}}{}_{}}^{}}$ ${\displaystyle {{}^{}{}_{}{}^{}}^{}}$ p${\displaystyle {{}^{}}^{}}$) ${\displaystyle 1^{}}$/ p ${\$\$u\_{p}=\left(\sum _{i=1}^{N} u_{p}\$$ri$}\$right)^{1/p}}$는 표준$$ p${p}$이다.

$데이터{\displaystyle \stackrel{}{}}$ 포인트 $x{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$$displaystyle$$x_{i$$}$의 스칼라 평균과$$ y $}{\$$displaystyle y_{i}$의 ${\displaystyle {평균}_{}}$을 $나타내는{\displaystyle \stackrel{}{}}$ $\beta {\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$ ${\bar {y},$β 0 {\${\displaystyle {displaystyle}_{\mathrm{}}}$ $\beta _{0}$에 대한 결과 추정치는 $\beta {\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle {\stackrel{}{^}}_{}}$ 0${\displaystyle {}_{}}$= 0이다$$.${\displaystyle \stackrel{}{y}\text{'}-\text{'}{\stackrel{\text{'}}{}}^{}}$ ${\displaystyle T^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {\hat {\beta }_{0}={\bar{y$}-{\$x}^{T}\beta$ $\}\}\}$ 이렇게 해서

${\displaystyle y_{i}-{\hat {\reat }}{0}-x_{i}^{T}\beta =y_{i}-({\bar {y}-{\bar {x}^{T}\beta )-x_{i}^{T}\beta =(y_{i}-{\bar {y})--(x_{i}-{\bar {x})^{{x}}T}\beta ,}$

따라서 영점 조정된 변수를 사용하는 것이 표준이다.또한 공변량은 일반적으로 용액이 ${\displaystyle \underset{}{\overset{}{\mathrm{측정}}}}$ 척도에 ${\displaystyle \underset{}{\overset{}{}}{}_{}^{}}$ 달라지지 않도록$$ $\$로 표준화된다$.{\displaystyle }$

다시 쓰는 것이 도움이 될 수 있다.

${\displaystyle \min \mathb {R} \mathb {}^{p}\left\{1}{1}{{1}{{1}{{{1}}\frac {1}{{{N}\fr}\{{}}\^{2}\right\}}}}}{{{{{1}\leq}}}}}}}}}}}}}}}}}의 적용을 받는다.$

소위 라그랑지 형식으로

${\displaystyle \min _{\beta \in \mathb {R}^{p}\left\{1}{1}{{1}\frac {1}{1}}\{{{N}\n}\we-X\beta \right\ _{2}^{2}+\lambda \beta \}}}}}}}}}}$

$여기$서 t ${\displaystyle t}$과(와) $\lambda {\displaystyle }$ ${\displaystyle \lambda }$ 사이의 정확한 관계는 데이터에 의존한다$$.

직교 공변량

이제 라소 추정기의 몇 가지 기본적인 성질을 고려할 수 있다.

공변량이${\displaystyle }$( x ${\displaystyle i_{}}$ ${\displaystyle {}_{}}$ x ${\displaystyle j_{}}$) =${\displaystyle {}_{}}$ ${\displaystyle i_{}}$ j ${\$이 되도록 먼저 직교라고 가정함$=\delta _{ij}}$, where ${\displaystyle (\cdot \mid \cdot )}$ is the inner product and ${\displaystyle \delta _{ij}}$ is the Kronecker delta, or, equivalently, ${\displaystyle X^{T}X=I}$, then using subgradient methods it can be shown that

${\displaystyle {\begin{aigned}{\hat{\beta}}}}{}}{{n_\lambda }({\hat {\beta }}}}^{\text}OLS}}={\hat{\beta }}}}^{\text{OLS}\max \left (0,1-{\frac {N\lambda }}{{\hat {\\beta}}}}{j}^{\text{\cHTER}OLS}}}\\오른쪽)\\&{\text{where }{\hat {\property }^{\text{{\text}OLS}}=(X^{T}X)^{-1}X^{{1}X^{T}y\end{aigned}}$ ^[2]

${\displaystyle S_{}}$ ${\displaystyle {\alpha }_{}}$ ${\$은(는) 작은 값을 0으로 설정하고 큰 값을 하드 임계값 연산자로 손대지 않고 0을 향해 정확하게 0으로 변환하기 때문에 소프트 임계값 연산자로 일컬어지며$$, 종종 $H{\displaystyle {}_{}}$ ${\displaystyle {\alpha }_{}}$ ${\$}로 표시된다.$\}\}\}.$

능선 회귀 분석의 목적은 최소화하는 것이다.

${\displaystyle \min \in \mathb {R}^{p}\좌측\{\{\frac {1}{1}{{N}\y-X\beta \_{2}^{2}+\lambda \\\\\\\beata \{2}^ \{2}^{2}\{2}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

양보하는

${\displaystyle {\hat {\beta }}_{j}=(1+N\lambda )^{-1}{\hat {\beta }}}^{j}^{\text{\cHot{}}OLS}}.}$

리지 회귀 분석은 모든 계수를 균일한 계수$({\displaystyle 1}$+ N ${\displaystyle \lambda {}^{}}$)${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$ ${\$로 축소하고$$ 계수를 0으로 설정하지 않는다.

또한 최소화하는 것이 목표인 최량 부분 집합 선택을 사용한 회귀 분석과도 비교할 수 있다.

${\displaystyle \min _{\beta \in \mathb {R}^{p}\left\{1}{1}{1}{1}{{1}{{{N}\n}\wefrac {1}\x\beta \right\ _{2}^{2}+\lambda \beta \}}}}}}}}}}}}}$

여기서 $\Vert {\displaystyle }$ ${\displaystyle {}_{}}$ ${\$\_${0$}}은 "${\displaystyle {\ell \mathrm{}}^{}}$ 0 ${\$으로, z의 m 성분이 0이 아닌 경우$$ $\Vert {\displaystyle }$ ${\displaystyle z}$ ${\displaystyle \Vert }$= ${\displaystyle m}$ ${\displaysty$\$z\ =m}$로 정의된다.이 경우, 라는 것을 보여줄 수 있다.

${\displaystyle {\hat {\pair }_{j}=H_{\sqrt{{N\lambda}}}}}\왼쪽({\hat {\beta }}}}}{j}^{\text}{\text}}OLS}\오른쪽)={\hat{\hat}}_{j}^{\text{OLS}}\mathrm {I} \left(\왼쪽 {\hat {\beta }}}_{j}^{\text{\text}OLS}\오른쪽 \geq {\sqrt {N\lambda }}\오른쪽)}$

여기서 $H{\displaystyle {}_{}}$ ${\displaystyle {\alpha }_{}}$ ${\$은(는) 소위 하드 임계값 기능이고 $I{\displaystyle \mathrm{}}$ ${\$그$$ 인수가 참이면 1이고 그렇지 않으면 0) 표시 함수다.

따라서 라소는 최적의 부분 집합 선택 사례에서처럼 모든 계수의 크기를 축소하고 일부 계수의 크기를 0으로 설정하기 때문에 능선 및 최적 부분 집합 선택 회귀 분석의 특징을 모두 공유한다.또한, 능선 회귀 분석은 모든 계수의 스케일을 상수 인수로 하는 반면, 라소는 계수를 상수 값으로 환산하고 계수가 도달하면 0으로 설정한다.

상관 공변량

In one special case two covariates, say j and k, are identical for each observation, so that ${\displaystyle x_{(j)}=x_{(k)}}$, where ${\displaystyle x_{(j),i}=x_{(k),i}}$. Then the values of ${\displaystyle \beta _{j}}$ and ${\displaystyle \beta _{k}$라소 목적 기능을 최소화하는$$ $}$은(는) 고유하게 결정되지 않는다.In fact, if some ${\displaystyle {\hat {\beta }}}$ in which ${\displaystyle {\hat {\beta }}_{j}{\hat {\beta }}_{k}\geq 0}$, then if ${\displaystyle s\in [0,1]}$ replacing ${\displaystyle {\hat {\beta }}_{j}}$ by ${\displaystyle s({\hat{\beta }}_j+{\hat{\beta }}_{}}$${\displaystyle s({\hat {\beta }}_{j}+{\hat {\beta }}_{k})}$ and ${\displaystyle {\hat {\beta }}_{k}}$ by ${\displaystyle (1-s)({\hat {\beta }}_{j}+{\hat {\beta }}_{k})}$, while keeping all the other ${\displaystyle {\hat {\beta }}_{i}}$ fixed는 새로운 해결책을 제공하므로, 라소 객관적 기능은 일련의 유효한 미니마이저들을 가지고 있다.^[5]이 단점을 해결하기 위해 엘라스틱 네트 정규화를 포함한 몇 가지 라소의 변형들이 고안되었다.

일반형식

라소 정규화는 일반화된 선형 모델, 일반화된 추정 방정식, 비례 위험 모델 및 M-추정기와 같은 다른 객관적 기능으로 확장될 수 있다.^[2][3]목표함수 부여

${\displaystyle {\frac {1}{N}\sum _{i}^{{N}f(x_{i},y_{i},\alpha ,\beta )}$

에 대한 해답은 라스로 정규화.

${\displaystyle \min _{\alpha ,\beta }{{1}{1}{{N}\sum _{i}{N}^{N}f(x_{i}},\alpha ,\beta ){\text{}\}\beta \{{1}\leq t}의 적용을 받는다.$

${\displaystyle {여기}_{}}$서 $\beta {\displaystyle {}_{}}$ ${\displaystyle \property}$만 $벌칙$을 적용하고$α$ {\displaystyle $\property_{0}$은(는$)$ 기본 사례에서 벌칙을 적용하지$$ 않은 것처럼 허용되는 값을 자유롭게 취할 수 있다$$$$.

해석

기하학적 해석

라소는 계수를 0으로 설정할 수 있지만 표면적으로 유사한 능선 회귀 분석은 할 수 없다.이는 제약 경계 모양의 차이 때문이다.라소와 능선 회귀 모두 동일한 목표 함수를 최소화하는 것으로 해석할 수 있다.

${\displaystyle \min _{\beta _{0}\beta _\좌측\{1}{{1}\frac {1}{{1}\{{{1}-X\beta \우측\{2}^{2}^}\우측\}}}}$

그러나 다른 제약조건에 대해서는$$ 다음과 같다:${\displaystyle \beta }$ β β 1${\displaystyle {}_{}}$β ${\displaystyle {}_{}t}$ ${\displaystyle \ \cHB$${\displaystyle {}_{}^{}}$$cHB$ $\{1$}\$leq$t},${\displaystyle }$β ${\displaystyle \beta }$ ${\displaystyle {2\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}\beta }$ t ${\displaysty$\ \$i1}^{2}\leq t}$그림에는 $\ell {\displaystyle {}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$ ${\$} 표준에$$ 의해 정의된 제약 영역은 그 모서리가 축(일반적으로 교차 폴리토프)에 놓이도록 회전된 사각형인 반면, $\ell {\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$ 표준에$$ 의해 정의된 영역은 원(일반적으로 n-sphere)이며, 회전 불변하며, th따라서, 구석이 없다.그림에서 볼 수 있듯이, 표시된 선과 같이 경계에 접하는 볼록한 물체는 하이퍼큐브의 코너(또는 고차원 등가물)에 부딪힐 가능성이 높은데, 여기에 대한 $\beta {\displaystyle }$ ${\displaystyle \beta }$의 일부 구성요소는 동일하게 0인$$ 반면, n-sphere의 경우, 일부 구성요소가 있는 경계의 점들이 있다.$\beta {\displaystyle }$ ${\displaystyle \property }$의 구성 요소는 0이며$$ 볼록 물체는 $\beta {\displaystyle }$ ${\displaystyle \property }$의 일부 구성 요소가 0인$$ 지점에 더 이상 접촉할 가능성이 없으며, 이들 구성 요소 중 어느 것도 0인 지점에 도달하지 않는다.

정확성-단순성 트레이드오프를 통해 λ의 해석 용이성 향상

라소의 크기를 조정하여 주어진 값인$\lambda {\displaystyle }$ {\$displaystyle$ \$lambda }$과(와) 관련된 축소 정도를 예측하고 영향을 미치도록 할 수 있다$.$^[6] X ${\displaystyle X}$은(는) z-점수로 표준화되고 y ${\displaysty y}$은(평균 0) 중심인 것으로 가정한다.$\beta {\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$이 귀무 가설의 회귀 계수를 $나타내고{\displaystyle {}_{}}$ ${\displaystyle b_{}}$ ${\displaystyle O_{}}$ L S$${\$displaystyle b_{}$가 되도록 한다.$OLS}$은(는) 데이터에 최적화된 일반 최소 제곱 솔루션을 가리킨다$$.그런 다음 우리는 데이터 최적화 솔루션의 표본 내 정확성과 가설의 값을 고수하는 단순성 사이의 트레이드오프로 라그랑지안을 정의할 수 있다.^[7]결과적으로

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {(y-X\beta )'(y-X\beta )}{(y-X\beta _{0})'(y-X\beta _{0})}}+2\lambda \sum _{i=1}^{p}{\frac { \beta _{i}-\beta _{0,i} }{q_{i}}}\right\}}$

여기서 ${\$는 다음과$$ 같이 지정된다.첫 번째 분수는 상대적 정확도, 두 번째 분율 상대적 단순성, 그리고 두 $가지{\displaystyle }$ 사이의 균형 ${\displaystyle \lambda }$을(를) 나타낸다.

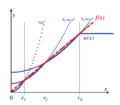
Given a single regressor, relative simplicity can be defined by specifying ${\displaystyle q_{i}}$ as ${\displaystyle b_{OLS}-\beta _{0} }$, which is the maximum amount of deviation from ${\displaystyle \beta _{0}}$ when ${\displaystyle \lambda =0}$. Assuming that ${\displaystyle {\beta }_{}}$${\displaystyle 0_{}}$= ${\displaystyle 0}$ ${\displaystyle \beta _{0}=0$ 솔루션 경로는 ${\displaystyle {R\mathrm{}}^{}}$ $2{\displaystyle {}^{}}$ ${\$ R$^{2$

${\displaystyle b_{\ell _{1}={\begin{case}(1-\lambda /R^{2})b_{{{}OLS}&{\mbox{{}}}}}\lambda \leq R^{2},\0&{\mbox{if}}\lambda >R^{2}.\end{case}}}$

$\lambda {\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle \lambda =0}$인 경우$,$ 일반 최소 제곱 용액(OLS)이 사용된다.The hypothesized value of ${\displaystyle \beta _{0}=0}$ is selected if ${\displaystyle \lambda }$ is bigger than ${\displaystyle R^{2}}$. Furthermore, if ${\displaystyle R^{2}=1}$, then ${\displaystyle \lambda }$ represents the proportional influence of ${\displays$$tyle \reason _{0}=0$$즉{\displaystyle }$, × ${\displaystyle 100}$%${\displaystyle \lambda$ \lambda $\times 100\%}$은(는) 데이터 최적화 OLS 솔루션에 대한 가설 값 영향의 최소량을 백분율로 측정한다$$.

$\ell {\displaystyle {}_{}}$ ${\$-norm을$$ 사용하여 단일 regressor가 주어지는 0으로부터의 편차를 벌충하는 경우, 솔루션 경로는 다음과 같다.

${\$$OLS}}$. Like ${\displaystyle b_{\ell _{1}}}$, ${\displaystyle b_{\ell _{2}}}$ moves in the direction of the point ${\displaystyle (\lambda =R^{2},b=0)}$ when ${\displaystyle \lambda }$ is close to zero; but unlike ${\displaystyle b_{\ell _{1}}}$, the$R{\displaystyle }$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$ $b{\displaystyle {}_{}}$ ${\displaystyle {\ell {}_{}}_{}}$ ${\displaystyle {{2\mathrm{}}_{}}_{}}$ ${\$ ${\displaystyle \lambda}}$이(가) 증가하면$$ 영향력이$$ 감소한다$$(그림 참조).
복수의 리레스터를 주어진 경우, 파라미터를 활성화하는 순간(즉, ${\displaystyle {\beta \mathrm{}}_{}}$ 0 ${\$도 $R{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$ 정확도에$$ 대한 레지스터의 기여에 의해 결정된다.일단.

${\displaystyle R^{2}=1-{\frac {(y-Xb)')}{{(y-X\beta _{0}}}{(y-X\beta _{0})}}}.}$

$R{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$의 75%는 가정된 ${\displaystyle {\beta \mathrm{}}_{}}$ 0 ${\$ 값$$ 대신 제한되지 않은 OLS 솔루션을 사용할 경우 샘플 내 정확도가 75% 향상됨을 의미한다.각 가설에서 벗어나는 개별 기여는 $p{\displaystyle }$ ${\displaystyle p}$ x$$ $p{\displaystyle }$ ${\displaystyle p}$ 행렬로$$ 계산할 수 있다.

${\displaystyle R^{\otimes }=(X'{\tilde{y}}_{0})(X'X)^{-1}({\tilde{y}}}}{\tilde {y}}}}{\tilde {y}}}{0}}}}^{-1},},}$

여기서 $y{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 0_{\mathrm{}}}$= y${\displaystyle }$- ${\displaystyle X}$ ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle {y}_{0}=y-X\beta _{$0$\}.$ $if{\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle O_{}}$ ${\displaystyle L_{}}$ ${\displaystyle S_{}}$ ${\$${\displaystyle {OLS\mathrm{}}^{}}$$}}$ $R{\displaystyle {}^{}}$ 2 ${\$ R$^{2}}$회$$ 계산하면$$ R${\displaystyle {}^{}}$⊗ ${\$ R$^{\otimes }}}}$의 대각선 원소가 ${\displaystyle {R\mathrm{}}^{}}$ $2{\displaystyle {}^{}}$ ${\$ R$^\{$$2}}.$대각선 $⊗{\$ 값은$$ 0보다 작거나 1보다 작을 수 있다.Regressor가 상관 관계가 없는 경우, $R{\displaystyle {}^{}}$ ${\displaystyle {\otimes }^{}}$ ${\$ i$^{{\otimes }}}$의 ${\displaystyle i^{}}$ t h ${\$displaystyle r^{\$otimes$$}}}}$ 대각선$$ 요소에 단순히$$ ${\displaystyle x_{}}$ $i{\displaystyle {}_{}}$ ${\$$}$와 $y{\displaystyle }$ ${\displaystysty$ y} $사이$의 r^{} $값$에 해당된다$.$

의 적응 lasso의 rescaled 버전, 나는 OLSb원q 적응 lasso을 설정하여 얻을 수 있어요, 만약 regressors 있uncorrelated β 0, 나는{\displaystyle q_{{\mbox{적응 lasso}} 난})b_{OLS,i}-\beta _{0,i}}.[8], 그 순간은 나는 하루에 500파운드 h{\displaystyle i^{월}}파라미터를 활성화에 의해서 주어진다 −.월e $i{\displaystyle {}^{}}$ t ${\displaystyle h^{}}$ ${\$ i$^{{0}}$$⊗{\$ $\}\}\}\}$의 대각선$$ 원소. $\beta {\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$이 0의 벡터라고$$ 가정하면,

${\displaystyle b_{i}={\begin{case}(1-\lambda /R_{i}^{\otimes }b_{{}}}}{{}b_{{}}}}}}}}}}{.OLS,i}&{\mbox{{}}}}}}\lambda \leq R_{i}^{\notimes }}\\0&{\mbox{}}}}}}}}\end{case}}}$

즉, regressor와 상관관계가 없는 $경우{\displaystyle }$, ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle \lambda }$은(는) $\beta {\displaystyle {}_{}}$ 0 ${\$의 최소 영향을 다시$$ 지정한다$.$ regressor가 상관관계가 있는 경우에도 $\lambda {\displaystyle }$ ${\displaysty$ \$lambda }$이 가장 높은 대각 요소와$$ 같을 때 회귀 파라미터가 활성화된다.$R$ R$^{\otimes$ $\}\}\}.$

These results can be compared to a rescaled version of the lasso by defining ${\displaystyle q_{{\mbox{lasso}},i}={\frac {1}{p}}\sum _{l} b_{OLS,l}-\beta _{0,l} }$, which is the average absolute deviation of ${\displaystyle b_{$$\beta {\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$의 OLS$\}.$ regressor가 상관관계가 없다고 가정할 때 ${\displaystyle i^{}}$ t ${\displaystyle h^{}}${\$displaystyle i$^{$th}}$ regressor의$$ 활성화 순간은 다음과 같다.

${\displaystyle {\lambda }}}{{\text{lasso}},i}={\frac {1}{p}}{\sqrt{R_{i}^{\otimes }}\{l=1}^{p}\sqrt{R_{l}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.}$

For ${\displaystyle p=1}$, the moment of activation is again given by ${\displaystyle {\tilde {\lambda }}_{{\text{lasso}},i}=R^{2}}$. If ${\displaystyle \beta _{0}}$ is a vector of zeros and a subset of ${\displaystyle p_{B}}$ relevant parameters are equally responsib${\displaystyle {r\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$= ${\displaystyle 1}$ ${\displaystyle R^{2}=1}$의 완벽한 적합을 위해$$이 부분 집합은 1 ${\displaystyle \frac{p}{}}$ ${\displaystyle \lambda }$ 값$$ 1 p ${\$에서 활성화된다$.$The moment of activation of a relevant regressor then equals ${\displaystyle {\frac {1}{p}}{\frac {1}{\sqrt {p_{B}}}}p_{B}{\frac {1}{\sqrt {p_{B}}}}={\frac {1}{p}}}$. In other words, the inclusion of irrelevant regressors delays the moment that relevant regressors are activated by this 재질의 라소적응형 라소와 라소는 '1ASTC' 추정기의 특별한 경우다.후자는 regressor 사이의 절대 상관관계가 사용자 지정 값보다 큰 경우에만 파라미터를 함께 그룹화한다.^[6]

베이지안 해석

능선회귀는 계수에 정상적인 사전분포가 할당된 선형회귀로 해석할 수 있듯이, 라소는 계수에 라플라스 이전분포가 있는 선형회귀로 해석할 수 있다.라플라스 분포는 0(첫 번째 파생상품은 0으로 불연속됨)으로 급격히 정점을 이루며, 정규 분포보다 확률 질량을 0에 더 가깝게 집중시킨다.이는 라소가 일부 계수를 0으로 설정하는 경향이 있는 반면, 능선 회귀 분석은 그렇지 않은 이유에 대한 대체 설명을 제공한다.^[2]

볼록 이완 해석

또한 라소는 최상의 부분 집합 선택 회귀 문제의 볼록한 완화로 볼 수 있는데, 이는 일부 $고정{\displaystyle }$ k ${\displaystyle \le n}$ ${\$$displaystyle \leq k}$ 공변량의$$ 목표 함수 값 중 가장 작은 값을 초래하는 $\le {\displaystyle }$ ${\displaystyle k}$ ${\$$displaystyle k\leq n}$의 부분 집합을 찾는 것이다$.$ 여기서 n은 공변량의 총 수입니다.The "${\displaystyle \ell ^{0}}$ norm", ${\displaystyle \ \cdot \ _{0}}$, (the number of nonzero entries of a vector), is the limiting case of "${\displaystyle \ell ^{p}}$ norms", of the form ${\displaystyle \textstyle \ x\$$_{p}=\left(\sum _{i=1}^{n} x_{j} ^{p}\right)^{1/p}}$ (where the quotation marks signify that these are not really norms for ${\displaystyle p<1}$ since ${\displaystyle \ \cdot \ _{p}}$ is not convex for ${\displaystyle p<1}$, so the triangle inequality does not hold).따라서 p = 1은 "${\displaystyle {\ell }^{}}$ p ${\$규범$$"이 볼록(따라서 실제로 표준)인 가장 작은 값이기 때문에, las x so${\displaystyle {t\mathrm{}}_{}}$ ${\displaystyle \x\ _{1}\leq t}$에 의해 정의된 영역이 선체의 볼록이기 때문에, 어떤 의미에서는 최상의 서브셋 선택 문제에 대한 최고의 볼록 근사이다.< $displaystyle \$ x$\$에서 p < 1 ${\displaystyle p<1}$에 대해 정의된 영역

일반화

라소 변형은 원래 기법의 한계를 고치고 그 방법을 특정 문제에 더 유용하게 만들기 위해 만들어졌다.이 모든 것들은 공변량들 사이의 의존성을 존중하거나 이용하는데 초점을 맞추고 있다.

탄성 순 정규화는 예측 변수의 수가 표본 크기보다 클 때 성능을 향상시키고, 강하게 상관된 변수를 함께 선택할 수 있게 하며, 전체적인 예측 정확도를 향상시키는 능선 회귀와 같은 페널티를 추가한다.^[5]

그룹 라소는 관련 공변량 그룹을 단일 단위로 선택할 수 있도록 하는데, 다른 공변량 없이 일부 공변량을 포함하는 것이 말이 되지 않는 설정에 유용할 수 있다.^[9]그룹 라소의 추가 확장은 개별 그룹 내에서 가변 선택을 수행하고 그룹 간 중첩을 허용한다(오버랩 그룹 라소).^[10][11]

퓨전된 라소는 문제의 공간적 또는 일시적 특성을 설명할 수 있으며, 시스템 구조와 더 잘 일치하는 추정치를 도출한다.^[12]라소 정규화된 모델은 하위 각도 방법, 최소 각도 회귀 분석(LARS), 근위부 그라데이션 방법을 포함한 기법을 사용하여 적합할 수 있다.정규화 매개변수에 대한 최적 값을 결정하는 것은 모델이 잘 수행되는지 확인하는 중요한 부분이다. 일반적으로 교차 검증을 사용하여 선택된다.

탄성망

2005년 조우(Zou)와 헤스티(Heastie)가 탄성 그물을 선보였다.^[5]p > n (공변량의 수가 표본 크기보다 큰 경우) 라소는 공변량을 n개만 선택할 수 있고(결과와 더 많은 공변량이 연관되어 있는 경우에도) 상관성이 높은 공변량 집합에서 하나의 공변량을 선택하는 경향이 있다.또한 n > p에도 불구하고, 강하게 상관된 공변량이 주어지면 능선회귀가 더 잘 수행되는 경향이 있다.

탄력 그물은 $\ell {\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$}} 벌칙$$ 조건 부여를 추가하여 라소를 확장한다.

${\displaystyle \min \mathb {R}^{p}\좌측\{\\\\n\i-X\beta \right\_{2}^{2}+\lambda _{1}\\\{1}\{1}\}\{1}\{1}\lamba \{2}^{2}오른쪽}}}$

어떤 것이 해결과 맞먹는다.

${\displaystyle {\begin{aligned}\min _{\beta _{0},\beta }\left\{\left\ y-\beta _{0}-X\beta \right\ _{2}^{2}\right\}&{\text{ subject to }}(1-\alpha )\ \beta \ _{1}+\alpha \ \beta \ _{2}^{2}\leq t,\\&{\text{ where }}\alpha ={\frac {\lambda _{2}}{\lambda _{1}+\lambda _{2}}}.\end{정렬}}}$

이 문제는 간단한 라소 형태로 쓰여질 수 있다.

${\displaystyle \min _{\beta ^{*}\mathb {R} ^{p}\{p}\{p}\\{*-X^{*}\*}\beta ^{2}+\lambda ^{*}\\{1}\{1}\right\}}}}}}}}}}}}$

내버려 두는

${\displaystyle X_{(n+p)\times p}^{*}=(1+\lambda _{2})^{-1/2}{\binom {X}{\lambda _{2}^{1/2}$$I_{p\times p}}}}$, ${\displaystyle y_{(n+p)}^{*}={\binom {y}{0^{p}}},\qquad \lambda ^{*}={\frac {\lambda _{1}}{\sqrt {1+\lambda _{2}}}}}$, ${\displaystyle \beta ^{*}={\sqrt {1+\lambda _{2}}}\beta .}$

그러면 $\beta {\displaystyle \hat{}}$ =${\displaystyle \frac{\sqrt{{}_{}}}{}}$ ${\displaystyle \frac{{\stackrel{}{^}}^{}}{}}$ ${\displaystyle \frac{{^}^{}}{}}$ ${\displaystyle \frac{{}^{}}{\sqrt{\mathrm{}}}}$ + $+$ ${\displaystyle \frac{\sqrt{{2\mathrm{}}_{}}}{}}$ {\$displaystyle {\hat$ {\$beta }}={\frac {{\$frac {{\$hat {\beta }^{*}}}{\sqrt{1+\lambda _{2$이 되는데, 공변량이 서로 직교할 때 이 경우

${\displaystyle {\hat {\beta }}_{j}={\frac {{\hat {\beta }}_{j}^{\text{*,OLS}}}{\sqrt {1+\lambda _{2}}}}\max \left(0,1-{\frac {\lambda ^{*}}{\left {\hat {\beta }}_{j}^{\text{*,OLS}}\right }}\right)={\frac {{\hat {\beta }}_{j}^{\text{OLS}}{1+\lambda _{2}}\max \left(0,1-{\frac {\lambda _{1}}{1}}{{1}}}}\좌측 {\hat{\beta}^{j}^{\text{,}OLS}}\{}\오른쪽)=(1+\lambda _{2}^{-1}{\hat {\beta }}^{j}^{\text{lasso}}}}.}$

그래서 탄력적인 순벌칙의 결과는 라소와 능선벌칙의 효과를 합친 것이다.

일반적인 사례로 돌아가면, 이제 페널티 기능이 엄격히 볼록해진다는 것은 $x{\displaystyle {}_{}}$ ${\displaystyle {(j}_{}}$)${\displaystyle {}_{}}$= ${\displaystyle x_{}}$( k${\displaystyle {}_{}}$) ${\$$\beta {\displaystyle {\hat{}}_{}}$ j${\displaystyle {}_{}}$= ${\displaystyle {\beta }_{}}$^[5] ${\displaystyle k_{}}$ ${\$ $\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}$일반적으로 > ${\displaystyle {\hat {\beta }}{j}{\hat {\beta _{k}}}0}$

${\displaystyle {\frac {\hat {\beta}-{j}-{\hat {\beta _{k}}}{\\\y\}}}\lambda _{2}^1}{2}}}}{\cext{{}}}, 여기서 }\rho =X,}X}X}}}}}}}}$

$x{\displaystyle }$ ${\displaystyle x}$이($$가) 정규화되기 때문에 표본 상관 행렬인 경우.

따라서 상관성이 높은 공변량은 regression ${\displaystyle y}$ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$\ $y\ _{1},$ $\lambda {\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$}}$$모두에$$ 따라 유사도의 회귀 계수가 비슷한 경향이 있는데, 이는 라소와 다르다.강하게 상관된 공변량이 유사한 이 현상을 그룹화 효과라고 한다.유전자를 질병에 묶는 것과 같은 응용 프로그램에서는 라소처럼 각 상관 공변량 집합에서 하나를 선택하는 것보다 관련된 공변량을 모두 찾는 것이 바람직하므로 그룹화가 바람직하다.^[5]또한 각 그룹에서 한 개만 선택하면 모형이 덜 견고하기 때문에(그래서 리지 회귀가 라소를 능가하는 경우가 많다) 일반적으로 예측 오차가 커진다.

그룹 라소

2006년 위안과 린은 공변량의 사전 정의된 그룹을 모델 내외로 공동으로 선택할 수 있도록 그룹 라소를 도입했다.^[9]이는 많은 설정에서 유용하며, 아마도 가장 분명히 범주형 변수가 이항 공변량의 집합으로 코드화된 경우 유용할 것이다.이 경우 그룹 라소는 범주형 공변량을 인코딩하는 모든 변수를 함께 포함하거나 제외할 수 있다.그룹화가 자연스러운 또 다른 배경은 생물학 연구에 있다.유전자와 단백질은 흔히 알려진 경로에 놓여있기 때문에 어떤 경로가 결과와 관련이 있는지는 개별 유전자의 여부보다 더 중요할 수 있다.그룹 라소의 객관적 기능은 표준 라소 목표를 자연스럽게 일반화하는 것이다.

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{\left\ y-\sum _{j=1}^{J}X_{j}\beta _{j}\right\ _{2}^{2}+\lambda \sum _{j=1}^{J}\ \beta _{j}\ _{K_{j}}\right\},\qquad \ z\ _{K_{j}}=(z^{t}K_{j}z)^{1/2}}$

여기서 설계 행렬 $X{\displaystyle }$ ${\displaystyle X}$ 및 공변량$$ 벡터$\beta {\displaystyle }${\$displaystyle \beta }$이(가) 각 J 그룹에 하나씩 설계 행렬 X ${\displaystyle j_{}}$ ${\$ 및 공변량$$ 벡터 $\beta {\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$의 모음으로 대체되었다$$.덧붙여 벌칙항은 이제 ${\displaystyle {\ell \mathrm{}}^{}}$ 2 ${\$ $^{$$2$}}개의$$ 규범에 대한 합이 $된다$${\displaystyle {각}_{}}$ 공변량이 자신의 그룹에 속하고 ${\displaystyle K_{}}$ j${\displaystyle {}_{}}$= ${\displaystyle I}$ ${\displaystyle K_{j}=$에 의해 정의된다$I$ 그러면 표준 라소로 감소하는 반면, $K{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$= ${\displaystyle I}$ ${\displaystyle K_{1}=I}$만 있는 경우에는 능선 회귀로 감소한다$.$위약금은 각 그룹이 정의한 서브스페이스에서 $\ell {\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$ 표준으로$$ 감소하므로, 능선회귀가 할 수 없는 것처럼 그룹에서 일부 공변량만 선택할 수 없다.그러나 벌칙은 표준 라소에서와 같이 서로 다른 아공간 규범에 대한 합이기 때문에 제약조건에는 일부 비차이 포인트가 있어 일부 서브스페이스가 동일하게 0에 해당한다.따라서 일부 서브스페이스에 해당하는 계수 벡터를 0으로 설정하고 다른 서브스페이스는 축소할 수 있다.단, 각 그룹 서브 스페이스에 ${\displaystyle {\ell \mathrm{}}^{}}$ 1${\$페널티를$$ 추가하면 그룹 내 개별 공변량을 선택할 수 있는 이른바 스파스 그룹 라소까지 그룹 라소를 확장할 수 있다.^[10]또 다른 확장인 중첩된 그룹 라소는 예를 들어 유전자가 두 경로에서 발생하는 경우 그룹 간에 공변량을 공유할 수 있다.^[11]

퓨전라소

어떤 경우에는 연구 중인 현상이 시계열이나 영상 기반 데이터와 같이 분석 중에 반드시 고려해야 하는 중요한 공간적 또는 시간적 구조를 가질 수 있다.2005년에 티비시라니와 동료들은 이러한 유형의 데이터로 라소의 사용을 확장하기 위해 퓨전된 라소를 도입했다.^[12]퓨전된 라소 목표 기능은

${\displaystyle {\begin{aligned}&\min _{\beta }\left\{{\frac {1}{N}}\sum _{i=1}^{N}\left(y_{i}-x_{i}^{t}\beta \right)^{2}\right\}\\[4pt]&{\text{ subject to }}\sum _{j=1}^{p} \beta _{j} \leq t_{1}{\text{ and }}\sum _{j=2}^{p} \beta _{j}-\beta _{j-1} \leq t_{2}.\end{정렬}}}$

첫 번째 구속조건은 라소 구속조건인 반면, 두 번째 구속조건은 시간적 또는 공간적 구조와 관련하여 큰 변화를 직접적으로 벌하는 것으로, 계수가 시스템의 근본 논리를 반영하기 위해 부드럽게 변화하도록 강제한다.클러스터형 라소는^[13] 퓨전 라소의 일반화로, 그 효과에 따라 관련 공변량을 식별하고 그룹화한다(코퍼펙트).기본 아이디어는 0이 아닌 계수가 군집하도록 계수의 차이를 벌충하는 것이다.이는 다음과 같은 정규화를 사용하여 모델링할 수 있다.

$\displaystyle \sum _{i<j}^{p} \ft_{i}-\ft_{j} \leq t_{2}.}$

이와는 대조적으로 변수는 고도로 상관된 그룹으로 군집화하여 각 군집으로부터 하나의 대표적인 공변량을 추출할 수 있다.^[14]

융합된 라소 문제를 해결하는 알고리즘과 그것의 일부 일반화가 존재한다.알고리즘은 한정된 수의 운영에서 정확히 해결할 수 있다.^[15]

준규범 및 교량 회귀 분석

라소, 탄성 네트, 그룹, 퓨전 라소는 $penalty{\displaystyle {}^{}}$ ${\$및$$ $\ell {\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$2}}$개$의 규범$$(필요한 경우 가중치 포함)에서 페널티 기능을 구성한다.브리지 회귀 분석에서는 일반 ${\displaystyle {\ell }^{}}$ p ${\$규범$$(${\displaystyle \mathrm{p}}$ ${\displaystyle \ge }$ 1 ${\displaystyle p\geq$ 1$\})$과 퀘이시노름(<1> ${\displaystyle 0<p>)$^[17]을 사용한다.예를 들어, p=1/2의 경우, 라그랑지안 양식의 라소 목표의 아날로그는 해결하는 것이다.

${\displaystyle \min \mathb {R} \mathb {}^{p}\left\{1}{{1}{1}{{1}{{1}}\{{N}\n}\y-X\beta\right\ _{2}^{2}+\sqrt{\\\\{1/2}}}\rig}}}}}}}}}}}}}}}}}}}$

어디에

${\displaystyle \ \ \{1/2}=\left(\sum _{j=1}^{p}{\sqrt{\}{{j}}}}\right)^{2}}$

부분적 준규범 ${\displaystyle p^{}}$ p ${\$^{$p}($<< 1{\$displaystyle$ 0$<p<$1은 이론적, 경험적으로 데이터 분석에서 보다 의미 있는 결과를 제공한다고 주장한다.^[18]이러한 준규범들의 비합치성은 최적화 문제를 복잡하게 한다.이 문제를 해결하기 위해 기능 최소화를 위한 기대 최소화 절차를 개발하여^[19] 시행한다^[16].

${\displaystyle \min \mathb {R} \mathb {}^{p}\left\{1}{{1}{{{N}\좌측\y-X\beta\right\ _{2}^{2}^{j=1}^{p}}\vartheta(\j}{j}^}}오른쪽)}).$

where ${\displaystyle \vartheta (\gamma )}$ is an arbitrary concave monotonically increasing function (for example, ${\displaystyle \vartheta (\gamma )={\sqrt {\gamma }}}$ gives the lasso penalty and ${\displaystyle \vartheta (\gamma )=\gamma ^{1/4}}$ gives the ${\$디스플레이 $스타일 \ell ^{1/2}}$ 벌칙$$).

최소화를 위한 효율적인 알고리즘은 부분적인 2차적 근사치(PQSQ)에 기초한다.^[19]

적응라소

적응형 라소는 Zou가 선형 회귀^[20] 분석을 위해 2006년에, Zhang과 Lu가 비례 위험 회귀 분석을 위해 2007년에 도입했다.^[21]

선행라소

이전 라소는 장 외 연구진이 특정 공변량의 중요성과 같은 사전 정보를 통합하기 위해 2016년 일반화된 선형 모델에 도입했다.^[22]이전의 라소에서는 그러한 정보를 유사 반응(이전 반응이라고 함) ${\displaystyle y^{\mathrm{}}}$ ${\displaystyle {\stackrel{}{^}}^{}}$ p ${\$로 요약한 후$$ 라소 벌칙으로 통상적인 객관적 함수에 추가 기준 함수를 추가한다.일반성의 상실 없이 선형 회귀에서는 새로운 목적 함수를 다음과 같이 기록할 수 있다.

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {1}{N}}\left\ y-X\beta \right\ _{2}^{2}+{\frac {1}{N}}\eta \left\ {\hat {y}}^{\mathrm {p} }-X\beta \right\ _{2}^{2}+\lambda \ \beta \ _{1}\right\},}$

에 해당하는

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {1}{N}}\left\ {\tilde {y}}-X\beta \right\ _{2}^{2}+{\frac {\lambda }{1+\eta }}\ \beta \ _{1}\right\},}$

the usual lasso objective function with the responses ${\displaystyle y}$ being replaced by a weighted average of the observed responses and the prior responses ${\displaystyle {\tilde {y}}=(y+\eta {\hat {y}}^{\mathrm {p} })/(1+\eta )}$ (called the adjusted response values by the p더 높은 정보

이전 lasso에서는 매개 변수 $\eta {\displaystyle }$ ${\displaystyle \eta }$을(를) 밸런싱 매개 변수라고 부르는데$$, 이는 데이터와 이전 정보의 상대적 중요성의 균형을 맞춘다는 것이다.$극단적$인 ${\displaystyle =}$ = ${\displaystyle 0}$ ${\displaystyle \eta$ =$0}$의 경우$,$ 이전의 lasso는 lasso로 축소된다.만약 $\eta {\displaystyle }$= ${\displaystyle \mathrm{\infty }}$ ${\displaystyle \eta =\infully$ $\}$인 경우, 이전 라소는 모델에 적합한 사전 정보에 전적으로 의존할 것이다.또한 밸런싱 매개 변수 $\eta {\displaystyle }$ ${\displaystyle \eta }$은(는) 베이지안 관점에서 이전 분포의$$ $\beta {\displaystyle }$ ${\\displaystyle \beta }$의 분산을 제어한다는 또 다른 매력적인 해석을 가지고$$ 있다.

선행 라소는 선행정보가 고품질일 때 매개변수 추정과 예측(추정오차와 예측오차가 작음)에 더 효율적이며, 균형잡힌 매개변수 $\eta {\displaystyle }$ ${\displaystyle \eta }$을(를) 잘 선택하여 낮은 품질의 사전정보에 강하다$.$

라소 솔루션 컴퓨팅

라소의 손실 기능은 다를 수 없지만, 볼록 분석과 최적화 이론으로부터 다양한 기법이 개발되어 라소의 솔루션 경로를 계산하게 되었다.여기에는 좌표 강하,^[23] 하위 각도 방법, 최소 각도 회귀 분석(LARS) 및 근위부 그라데이션 방법이 포함된다.^[24]하위 단계적 방법은 모든 점에서 객관적 기능이 다를 수 없는 경우에 대한 구배 강하 및 확률적 구배 강하와 같은 전통적인 방법의 자연적 일반화다.LARS는 라소 모델과 밀접하게 연계된 방식으로, 모든 상황에서 성능이 좋지 않을 수 있지만 효율적으로 장착할 수 있도록 하는 경우가 많다.LARS는 완전한 솔루션 경로를 생성한다.^[24]근위 방법은 유연성과 성능 때문에 대중화되었고 활발한 연구의 한 분야다.방법의 선택은 특정한 라소 변종, 데이터 및 가용 자원에 따라 달라질 것이다.그러나 근위부 방법은 일반적으로 성능이 좋다.

정규화 파라미터 선택

정규화 매개변수(${\displaystyle }$ ${\displaystyle \lambda }$)를 선택하는 것은 라소의 기본 부분이다.좋은 값은 수축과 가변선택의 강도를 조절하기 때문에 라소의 성능에 필수적이며, 이는 적당히 예측 정확도와 해석성을 모두 향상시킬 수 있다.그러나 정규화가 너무 강해지면 중요한 변수가 생략되고 계수가 과도하게 축소되어 예측 역량과 회의 중 둘 다 해칠 수 있다.교차 검증은 종종 정규화 파라미터를 찾는 데 사용된다.

베이시안 정보 기준(BIC)과 Akaike 정보 기준(AIC)과 같은 정보 기준은 계산 속도가 빠르고 성능은 작은 표본에서 덜 변동하기 때문에 교차 검증보다 선호될 수 있다.^[25]정보 기준은 모델의 표본 내 정확도를 극대화하는 동시에 유효 매개변수/자유도를 저하시킴으로써 추정자의 정규화 매개변수를 선택한다.Zou 등은 0에서 벗어나는 매개변수의 수를 세어 유효 자유도를 측정할 것을 제안했다.^[26]모델의 자유도가 정규화 파라미터에 의해 더 강력한 불이익을 받을 경우에도 증가하기 때문에 카우프만과 로제트^[27], 잰슨 등은 자유도 접근에 결함이 있는 것으로 간주했다.^[28]대안으로 위에서 정의한 상대적 단순성 측정치를 사용하여 유효 매개변수 수를 계산할 수 있다.^[25]라소의 경우, 이 조치는 다음과 같다.

${\displaystyle {\hat {\mathcal {P}}}=\sum _{i=1}^{p}{\frac { \beta _{i}-\beta _{0,i} }{{\frac {1}{p}}\sum _{l} b_{OLS,l}-\beta _{0,l} }}}$,

정규화 매개 변수가 $\infty {\displaystyle \mathrm{}}$ ${\displaystyle \inflt }$에서 0으로 감소함에 따라$$ 단조롭게 $0$에서 p ${\displaystyle p}$으로 증가한다.

선택한 응용프로그램

라소(LASSO)는 경제·금융 분야에 적용돼 예측을 개선하고 기업 파산 예측 문헌이나 ^[29]고성장 기업 예측 등 때로는 방치된 변수를 선택하는 것으로 나타났다.^[30]

참고 항목

• 모델 선택
• 비모수 회귀 분석
• 티호노프 정규화

참조