부활절 날짜

부활절 날짜는 매년 computus('계산'을 뜻하는 라틴어)로 알려진 계산을 통해 결정됩니다.^[1][2][3] 부활절은 3월 21일 이후의 첫 보름달인 파스칼 보름달 이후의 첫 일요일에 기념됩니다(3월 분점의 고정된 근사치). 이 날짜를 미리 결정하려면 율리우스력 또는 그레고리력의 월, 날짜, 평일을 고려하면서 음력과 태양력 사이의 상관관계가 필요합니다.^[4] 이 알고리즘의 복잡성은 부활절 날짜를 예수가 십자가에 못 박힌 유대인의 유월절 날짜와 연관시키려는 욕구 때문에 발생합니다.^[5]

원래 매년 교황의 연례 발표를 통해 기독교 전체가 부활절 날짜를 받는 것이 가능했습니다. 그러나 3세기 초까지 로마 제국의 의사소통은 교회가 성직자가 독립적이지만 일관성 있게 스스로 날짜를 결정할 수 있는 시스템에 큰 가치를 둘 정도로 악화되었습니다.^[6] 또한 교회는 3월 분점에서 직접 부활절 날짜를 도출하여 히브리 달력에 대한 의존성을 없애고자 했습니다.^[7]

베데(Bede)는 시간의 기록(725)에서 테오필루스(Teophilus)의 부활절 주기를 "Paschal computus"라고 부르지만, 모든 종류의 계산을 위한 일반적인 용어로 계산을 사용합니다. 8세기 말에 이르러 컴퓨터는 시간의 계산을 구체적으로 언급하게 되었습니다.^[8] 율리우스력과 그레고리안력 중 어느 것을 사용하느냐에 따라 계산 결과가 달라집니다. 이 때문에 가톨릭교회와 개신교회(양력을 따르는 교회)는 동방정교회(율리우스력을 따르는 교회)와는 다른 날짜에 부활절을 기념합니다. 이는 관측된 분점으로부터 3월 21일의 표류로 달력의 그레고리안 개혁으로 이어졌고, 그들을 다시 일직선으로 되돌리기 위한 것이었습니다. 서기 2100년까지 3월 21일 율리우스력은 그레고리안 4월 3일을 의미합니다.

배경

부활절은 예수의 부활을 기념하는 것으로, 기독교인들은 유월절이 시작된 후 3일째(포함)에 일어났다고 믿고 있습니다. 히브리의 음력에서, 유월절은 니산 14일에 황혼에 시작합니다.^[9][10] 니산은 북반구에서 봄의 첫 달로, 14일은 보름달에 해당합니다. 2세기까지, 많은 기독교인들은 부활절을 오직 일요일에만 기념하기로 선택했습니다.^[11] 히브리 달력은 기독교 달력과 단순한 관계가 없습니다: 음력 새해 1월 1일 이전에 2년 또는 3년마다 윤달을 삽입하여 태양력과 다시 동기화됩니다. 후대의 유대인들은 메토닉 주기를 채택하여 미래의 인터칼레이션을 예측했습니다.

이 인터칼레이션의 가능한 결과는 14 니산이 춘분 이전에 발생할 수 있다는 것인데, 일부 3세기 기독교인들은 이를 받아들일 수 없다고 생각했습니다(오늘날 사용되는 고정된 달력에서는 발생할 수 없습니다).^[12] 결과적으로, 3월 분점 다음의 첫 보름달을 확인함으로써 부활절 날짜와 히브리 달력을 분리하기로 결정했습니다. 제1차 니케아 공의회(서기 325년) 무렵, 알렉산드리아 교회는 실제 천문 관측과 상관없이 3월 21일을 추분일로 지정했습니다. 395년 테오필루스는 부활절에 대한 미래의 날짜표를 출판하여 알렉산드리아 기준을 검증했습니다.^[13] 그 후, 첫 번째 기독교 보름달이 3월 21일 또는 그 이후에 첫 번째 일요일을 결정하는 절차가 계산이 될 것입니다.

역사

최초의 알려진 로마의 표는 222년 로마의 히폴리토스에 의해 8년 주기를 기준으로 고안되었습니다. 그 후 84년 표는 3세기 말경 아우구스티누스에 의해 로마에 소개되었습니다.^[a] 비록 19년의 메토닉 주기에 기초한 과정이 277년경 라오디케아의 아나톨리우스 주교에 의해 처음으로 제안되었지만, 4세기 후반 알렉산드리아 방식이 권위를 갖게 될 때까지 그 개념은 완전히 자리를 잡지 못했습니다.^[b]

알렉산드리아의 컴퓨터는 440년경 알렉산드리아 달력에서 율리우스력으로 변환되었고, 그 결과 437년에서 531년까지의 기간을 다루는 파스칼 표(알렉산드리아의 교황 키릴에 의한 것)가 작성되었습니다.^[16] 이 파스칼 표는 약 500년에서 540년까지 로마에서 일했던 디오니시우스 엑시구우스가 ^[17]532년에서 616년까지 이어지는 그의 유명한 파스칼 표의 형태로 그것의 연속을 구성하도록 영감을 준 원천이었습니다.^[18] 디오니시우스는 525년에 이 새로운 부활절 표를 출판함으로써 기독교 시대(그리스도의 화신으로부터 몇 년을 세는 것)를 소개했습니다.^[19][c]

수정된 84년 주기는 4세기 전반에 로마에서 채택되었습니다. 아키텐의 빅토리우스는 457년 알렉산드리아의 방식을 532년 표 형식으로 로마의 규칙에 적용하려고 했지만, 심각한 오류를 초래했습니다.^[20] 이 빅토리아 시대의 식탁들은 8세기 말에 디오니소스적인 식탁들에 의해 옮겨지기 전까지 갈리아(현재의 프랑스)와 스페인에서 사용되었습니다.

디오니시우스와 빅토리우스의 표는 영국 섬에서 전통적으로 사용되는 표와 충돌했습니다. 영국의 식탁은 84년 주기를 사용했지만, 한 오류로 인해 보름달이 너무 일찍 서서히 떨어졌습니다.^[21] 이러한 불일치로 인해 디오니소스 계통의 에안플 æ드 여왕은 손바닥 일요일에 금식을 했고, 노섬브리아의 왕인 남편 오스위우는 부활절 일요일에 잔치를 벌였다는 보도가 나왔습니다.

630년 아일랜드 마그-렌 시노드의 결과, 아일랜드 남부 사람들은 디오니소스적인 테이블을 사용하기 시작했고,^[23] 664년 휘트비 시노드 이후에는 영국 북부 사람들이 그 뒤를 이었습니다.^[24]

디오니소스적인 기록은 725년 베데에 의해 완전히 기술되었습니다.^[25] 샤를마뉴가 베데의 추종자인 알쿠인으로부터 782년에 프랑크 교회를 위해 채택했을 수도 있습니다. 디오니소스/베단 계산기는 그레고리력 개혁 이전까지 서유럽에서 사용되었고, 대다수의 동방 정교회와 비 칼케도니아 교회를 포함한 대부분의 동방 교회에서 사용되고 있습니다.^[26] 이 체계를 따르지 않는 유일한 동방 정교회는 그레고리안을 사용하는 핀란드 정교회입니다.

6세기 동안 알렉산드리아에서 벗어난 동방 아시리아 교회 등 옛 비잔티움 제국의 동쪽 변경지대를 벗어난 교회들은 ^[27]지금 532년마다 동방정교회와 4번씩 다른 날짜에 부활절을 기념하고 있습니다.^{[citation needed]}

로마 제국의 동쪽 가장자리에 있는 이 교회들을 제외하고, 10세기까지 모두 알렉산드리아 부활절을 채택했는데, 비록 베데는 이미 725년에 표류를 주목했지만, 16세기에는 더 멀리 표류했습니다.^[d] 더 나쁜 것은 부활절을 계산하는 데 사용된 것으로 추정되는 달이 19년 주기로 율리우스력에 고정되었다는 것입니다. 그 근사치는 310년마다 하루씩의 오차를 쌓았고, 그래서 16세기에 이르러 음력은 실제 달과 4일씩 어긋났습니다. 그레고리안 부활절은 1583년부터 로마 가톨릭 교회에 의해 사용되었고 1753년에서 1845년 사이에 대부분의 개신교 교회에 채택되었습니다.

독일 개신교 국가들은 1700년에서 1776년 사이에 천문학적 부활절을 사용했는데, 이는 Tycho Brahe가 Ven 섬에 있는 Uraniborg 천문대에서 관측한 태양과 달의 천문학적 위치를 기반으로 한 것이었고, 스웨덴은 1739년에서 1844년 사이에 사용했습니다. 이 천문학적인 부활절은 우라니보르 시간(TT + 51^m)을 사용하여 춘분 직후의 보름달 직후의 일요일이었습니다. 그러나 그 일요일이 유월절 주간의 첫 날인 유대인 날짜 니산 15일인 경우에는 현대의 유대인 방식에 따라 계산된 것으로 1주일 늦춰졌습니다.^[29]

이 니산 15 규칙은 1778년과 1798년 두 스웨덴 해에 영향을 미쳤는데, 그레고리안 부활절 1주일 전이 아니라 1주일 늦춰져서 그레고리안 부활절과 같은 일요일이 되었습니다. 독일의 천문학적 부활절은 1724년과 1744년 그레고리안 부활절 일주일 전이었습니다.^[29] 스웨덴의 천문학적 부활절은 1744년 그레고리안 부활절 일주일 전이었지만 1805년, 1811년, 1818년, 1825년, 1829년 일주일 후였습니다.^[29]

두 개의 현대 천문 부활절이 제안되었지만 어느 교회에서도 사용되지 않았습니다. 첫 번째는 1923년 콘스탄티노플 시노드에서 수정된 율리우스력의 일부로 제안되었고 두 번째는 1997년 알레포에서 열린 세계교회협의회에서 제안되었습니다. 둘 다 독일어와 스웨덴어 버전과 같은 규칙을 사용했지만 니산 15 규칙이 없는 현대 천문학 계산과 예루살렘 시간(TT + 221^hm)을 사용했습니다. 1923년 버전은 1924년, 1943년, 1962년 그레고리안 부활절 한 달 전에 천문학적 부활절을 두었지만 1927년, 1954년, 1967년에는 일주일 후에 두었을 것입니다.^[30] 1997년 버전은 한 달 앞당겨졌을 2019년을 제외하고 2000-2025년 동안 그레고리안 부활절과 같은 일요일에 천문학적 부활절을 배치했을 것입니다.^[31]

이론.

부활절 주기는 29일 또는 30일 길이의 음력으로 날짜를 묶습니다. 예외가 있습니다. 3월에 끝나는 달은 보통 30일이지만 윤년 2월 29일에 해당하면 31일이 포함됩니다. 이 그룹들은 달의 주기를 기반으로 하기 때문에, 장기적으로 음력의 평균 달은 29.53059일인 시노딕 달의 매우 좋은 근사치입니다.^[32]

음력에는 12개의 시노드 달이 있으며, 총 354일 또는 355일입니다. 음력은 365일이나 366일인 역년보다 11일 정도 짧습니다. 태양이 음력을 초과하는 요즘을 epact(그리스어: ἐπα κτα ὶ ἡμέρα ι, 번역)라고 합니다. épaktai hēmérai, lit. '간주일').^[33][34]

양력의 날에 추가해야 음력의 정확한 날을 얻을 수 있습니다. 에팩트가 30에 도달하거나 초과할 때마다 음력에 30일의 추가 인터칼러리즘 달(또는 색전월)을 삽입해야 합니다. 그러면 에팩트에서 30을 빼야 합니다. 찰스 휘틀리(Charles Whatly)는 다음과 같은 세부 사항을 제공합니다.

"그러므로 그 해를 3월로 시작하는 것은 (고대의 관습 때문에) 달이 3월에 끝나는 것은 30일, 그리고 4월에 끝나는 것은 29일, 그리고 다시 5월에 30일, 그리고 6월과 9일에 29일을 허락했습니다.

임파루나파리, 임파르나파리, 임파르나파리, 임파르나파리,
정상적으로 완전한 정신 착란이 발생합니다.

"첫째 달, 셋째 달, 다섯째 달, 일곱째 달, 아홉째 달, 열한째 달은 각각 30일의 계산에 따라 달이 달로 되어 있는데, 이 달을 파레스루나에라고 합니다. 그러나 둘째 달, 넷째 달, 여섯째 달, 여덟째 달, 열째 달, 열째 달을 파레스루나에라고 합니다. 또는 같은 달에 달을 달하되, 달을 달을 달을 달을 달을 달을 달을 달을 달을 달을 달을 달을 달을 달을 달을 달을 달을 달을 달을 달을 달이라고 합니다

— Wheatly 1871, p. 44

그리하여 음력은 율리우스력이 끝나는 달의 이름을 따왔습니다. 19년의 메토닉 주기는 19년의 열대 기간을 235개의 시노딕 달로 가정합니다. 따라서 19년 후에는 태양년에도 같은 방식으로 달이 떨어질 것이며, 그 영향이 반복되어야 합니다. 19년 동안 효과는 0(mod 30)이 아닌 19 × 11 = 209 ≡ 29(mod 30)만큼 증가합니다. 즉, 209를 30으로 나눈 값은 30의 배수가 아니라 29의 나머지를 남깁니다. 30일의 달을 추가하는 것만으로 보상이 이루어진다면 이것은 문제입니다.^[e] 그래서 19년이 지나면 그 영향을 하루 정도 보정해야 사이클이 반복됩니다. 이것은 소위 saltus lunae ("달의 도약")입니다. 율리우스력은 주기의 마지막 해인 7월 1일에 시작하는 음력의 길이를 29일로 줄임으로써 이를 처리합니다. 이를 통해 3개월 연속 29일 동안 사용할 수 있습니다.^[f]

율리우스력과 음력이 거의 같은 시기에 시작하는 지점에 위치함으로써 소금기와 7개의 추가 30일 달이 대부분 숨겨져 있었습니다. 추가 월은 1월 1일(3년), 9월 2일(5년), 3월 6일(8년), 1월 3일(11년), 12월 31일(13년), 9월 1일(16년), 3월 5일(19년)에 시작되었습니다.^[35][36] 19년 주기의 연도 순서 번호를 "황금수"라고 하며, 공식에 의해 부여됩니다.

GN = (Y mod 19) + 1

즉, 기독교 시대의 Y라는 해를 19로 나누고 나머지에 1을 더한 것이 황금수입니다. (일부 출처에서는 나머지를 복용하기 전에 1을 추가하도록 지정합니다. 이 경우 0의 결과를 황금 숫자 19로 처리해야 합니다. 위의 공식에서는 나머지를 먼저 취한 다음 1을 더하므로 이러한 조정은 필요하지 않습니다.)

19년의 주기는 4년 또는 5년의 윤년을 가질 수 있기 때문에 모두 같은 길이는 아닙니다. 그러나 4주기의 주기인 76년(캘리픽 주기)의 길이는 76 × 365 + 19 = 27,759일(한 세기의 나눗셈을 넘지 않는 경우)입니다. 이 시기에는 235 × 4 = 940개의 음력이 있으므로 평균 길이는 27759 / 940 또는 약 29.530851일입니다. 76 × 6 = 456개의 통상적인 명목상의 30일 음력 달과 같은 수의 통상적인 명목상의 29일 달이 있지만, 이 중 19개는 윤일에 하루 길어지고, 24개는 30일, 4개는 29일의 인터칼레이션 달이 있습니다. 이는 시노드 월의 실제 길이인 약 29.53059일보다 길기 때문에 계산된 파스칼 보름달은 그레고리안 계와 같이 보정하지 않는 한 천문학적 보름달과 비교하여 점점 더 길어집니다(아래 참조).

파스칼 또는 부활절은 3월 21일 또는 그 이후에 14일째 되는 해의 첫 번째 보름달입니다. 부활절은 14일째 되는 일요일(또는 같은 말을 하면 3주째 되는 일요일)입니다. 음력 3월은 항상 3월 8일부터 4월 5일까지 29일간의 날짜에 시작됩니다. 따라서 14일째는 항상 3월 21일부터 4월 18일 사이의 날짜에 해당되며(그레고리안 또는 율리우스력에서는 서양과 동양의 시스템에 해당됨), 다음 일요일은 반드시 3월 22일부터 4월 25일 사이의 날짜에 해당됩니다. 그러나 서양의 시스템에서는 부활절이 1900-2199년의 300년 기간 동안 3월 22일에 해당할 수 없습니다(아래 참조). 태양력에서 부활절은 날짜가 35일 범위 내에서 다양하기 때문에 움직일 수 있는 축제라고 불립니다. 그러나 음력에서 부활절은 항상 파스칼 음력의 세 번째 일요일이며, 추수감사절과 같이 한 달 안에 특정한 요일과 일주일에 고정되어 있는 어떤 휴일보다 더 "이동성"이 없습니다.

표의 방법

그레고리안 연산 체계의 개혁

이 섹션은 확인을 위해 추가 인용이 필요합니다. 이 섹션의 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주시기 바랍니다. 미가공 재료는 도전하여 제거할 수 있습니다. 출처 찾기: "부활절 날짜" – 뉴스·신문·도서·학자·JSTOR(2019년 3월) (이 템플릿 메시지 제거 방법 및 시기 알아보기)

1582년 그레고리력이 도입된 주된 동기가 연산 체계를 개혁하는 것이었기 때문에, 새로운 달력과 함께 그에 상응하는 연산 체계 방법론이 도입되었습니다.^[h] 일반적인 작업 방법은 여섯 개의 캐논에서 클라비우스에 의해 주어졌고(1582), 그의 해설서(1603)에서 완전한 설명이 뒤따랐습니다.^[37]

부활절 일요일은 파스칼 보름달 날짜 다음 일요일입니다. 파스칼 보름달 날짜는 3월 21일 이후의 기독교 보름달 날짜입니다. 그레고리안 방법은 매년의 효과를 결정함으로써 파스칼 보름달 날짜를 도출합니다.^[38] epact는 * (0 또는 30)에서 29일 사이의 값을 가질 수 있습니다. 1월 1일의 날짜(즉, 음력 날짜)를 하루 줄인 달의 나이입니다. 그의 저서 "The Easter computus"와 기독교 시대의 기원인 Alden A Mosshammer는 "이론적으로, epact 30 = 0은 태양과 결합할 때의 초승달을 나타냅니다. 1의 효과는 이론적으로 달의 첫 번째 초승달의 첫 번째 가시성을 나타냅니다. 달의 열네 번째 날을 세는 것은 그 시점부터입니다."^[39]

음력 10월 14일은 보름달의 날로 여겨집니다.^[40] 반대("보름달")의 순간이 가장 떨어지기 쉬운 음력의 날입니다. "신월"은 음력 1월 1일에 (해가 진 후 서쪽 하늘의 가느다란 초승달처럼) 보일 가능성이 가장 높습니다. 태양과 달의 결합은 "공백" (29일) 달의 29일째와 "만원" (30일) 달의 30일째인 전날에 떨어질 가능성이 가장 높습니다.

역사적으로 1년 동안의 파스칼 보름달 날짜는 메토닉 주기의 순서 번호인 황금수에서 발견되었으며, 이 주기는 19년마다 1월 1일에 달의 단계를 반복합니다.^[41] 이 방법은 그레고리오 개혁에서 표의 날짜가 약 2세기 후에 현실과 맞지 않기 때문에 수정되었지만, 에팩트 방법을 통해 1~3세기의 유효성을 갖는 단순화된 표를 만들 수 있습니다.^[42][43]

2014년에 시작된 현재의 메토닉 사이클에 대한 효과는 다음과 같습니다.

연도	2014	2015	2016	2017	2018	2019	2020	2021	2022	2023	2024	2025	2026	2027	2028	2029	2030	2031	2032
금으로 만든 번호	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
에팩트[i]	29	10	21	2	13	24	5	16	27	8	19	*	11	22	3	14	25	6	17
파스칼 보름달 날짜[44]	14 4월	3 4월	23 3월	11 4월	31 3월	18 4월	8 4월	28 3월	16 4월	5 4월	25 3월	13 4월	2 4월	22 3월	10 4월	30 3월	17 4월	7 4월	27 3월

보다시피, 특정 연도의 파스칼 보름달 날짜는 보통 전년도보다 11일 빠르거나 19일 후입니다. 예외는 주기의 1년, 6년, 17년에는 날짜가 18일만 늦고, 7년과 18년에는 전년보다 10일만 빠릅니다. 동방계(아래 참조)에서 파스칼 보름달은 보통 4일 후입니다. 19년 중 5년은 34일 후이고, 6년과 17년은 5일 후입니다. 왜냐하면 그 해에는 그레고리안 제도가 4월 26일 이전에 부활절을 유지하기 위해 파스칼 보름달을 평소보다 하루 일찍 놓았기 때문입니다. AD 2100년에는 그 차이가 하루 더 증가할 것입니다.

반추는 다음과 같은 방법으로 초승달 날짜를 찾는 데 사용됩니다. 1년 중 365일 전체의 표를 작성하십시오(윤일은 무시됩니다). 그런 다음 "*"(0 또는 30), "xix"(29), "i"(1)까지 아래쪽으로 로마 숫자로 모든 날짜를 표시하고 1월 1일부터 시작하여 연말까지 반복합니다. 그러나 매초마다 이러한 기간은 29일만 계산되며 날짜를 xxv(25)로 표시하고 xxiv(24)로 표시합니다. 따라서 13번째 기간(마지막 11일)을 길게 취급하고 "xxv"와 "xxiv"라는 라벨을 순차적인 날짜(각각 12월 26일과 27일)에 할당합니다.^[45]

30일 기간 동안 "xxv"가 있는 날짜에 "25"라는 레이블을 추가하지만 29일 기간 동안 "xxv"와 함께 "xxv"가 있는 날짜에 "25"라는 레이블을 추가합니다. 월의 길이와 epact 주기의 길이에 대한 분포는 2월을 제외하고 각 시민 달력 월이 동일한 epact 레이블로 시작하고 끝나는 것과 8월의 경우 이중 레이블 "xxv"/"xxiv"로 시작하지만 단일 레이블 "xxiv"로 끝나는 것을 제외하고는 동일한 epact 레이블로 시작합니다. 이 테이블은 달력이라고 불립니다. 어느 해의 기독교적인 초승달은 그 해의 일이 입력되는 날짜입니다.^[45]

예를 들어, 그 해의 에팩트가 27이라면, 그 해의 모든 날짜에 에팩트 라벨 "xxvii"(27)가 있는 기독교적인 초승달이 있습니다. 에팩트가 25이면 메토닉 주기 동안 기독교적인 초승달이 같은 날짜에 두 번 떨어지지 않도록 도입된 복잡한 문제가 있습니다. 유효한 에팩트 사이클에 epact 24가 포함된 경우(1900년 이후와 2199년까지의 사이클과 마찬가지로), 25의 에팩트는 기독교적인 초승달을 4월 4일에, 그렇지 않으면 4월 5일에("xv"라는 라벨을 붙입니다).^[45]

4월 4일을 주는 25의 효과는 황금 숫자가 11보다 클 경우에만 발생할 수 있습니다. 이 경우 epact 24와 함께 1년 후 11년이 됩니다. 예를 들어, 1954년 황금 숫자는 17, 에팩트는 25, 기독교적인 초승달은 4월 4일, 보름달은 4월 17일로 기록되었습니다. 부활절은 그렇지 않았더라면 어땠을지 4월 25일이 아니라 4월 18일이었습니다. 1886년 황금 숫자가 6이었던 것처럼 말이죠. 이 시스템은 메토닉 사이클당 7개월을 자동으로 삽입합니다.

표의 모든 날짜에 1월 1일부터 시작하여 "A"에서 "G"로 라벨을 붙이고 연말까지 반복합니다. 예를 들어, 1월 5일에 문자 "E"가 있는 첫 번째 일요일이 있다면, 문자 "E"가 있는 모든 날짜는 그 해의 일요일입니다. 그리고 "E"는 dies dominica (라틴어로 '주님의 날'이라는 뜻)에서 나온 그 해의 지배적인 글자라고 불립니다. 지배적인 문자는 매년 한 자리씩 뒤로 순환합니다. 2월 24일 이후의 윤년에는 일요일이 주기의 앞 글자에 해당하므로 윤년에는 두 개의 지배적인 글자가 있습니다. 첫 번째 글자는 앞 글자이고 두 번째 글자는 윤일 다음 글자입니다.

실제로 부활절을 계산할 목적으로, 이것은 1년 중 365일 내내 행해질 필요는 없습니다. 효과는 3월이 1월과 정확히 동일하게 나오기 때문에 1월이나 2월은 계산할 필요가 없습니다. 1월과 2월의 도미닉 레터를 계산할 필요를 방지하려면 3월 1일의 D부터 시작합니다. 3월 8일부터 4월 5일까지만 반응이 필요합니다. 이를 통해 다음과 같은 표가 생성됩니다.

라벨.	3월	DL	4월	DL
*	1	D
xxix	2	E	1	G
xxvii	3	F	2	A
xxvii	4	G	3	B
xxvi	5	A	4	C
25	6	B
xxv			5	D
xxiv	7	C
xxxiii	8	D	6	E
xxxii	9	E	7	F
xxxi	10	F	8	G
xxx	11	G	9	A
xix	12	A	10	B
18세	13	B	11	C
17세	14	C	12	D
16세	15	D	13	E
xv	16	E	14	F
xiv	17	F	15	G
xiii	18	G	16	A
xii	19	A	17	B
xi	20	B	18	C
x	21	C	19	D
ix	22	D	20	E
viii	23	E	21	F
vii	24	F	22	G
vi	25	G	23	A
v	26	A	24	B
iv	27	B	25	C
iii	28	C	26	D
ii	29	D	27	E
i	30	E	28	F
*	31	F	29	G
xxix			30	A

예를 들어, epact가 27일 경우(xxvii), 기독교적인 초승달은 xxvii라고 표시된 모든 날짜에 해당합니다. 기독교 보름달은 13일 후에 떨어집니다. 위의 표에서 볼 수 있듯이 3월 4일과 4월 3일에는 초승달이, 3월 17일과 4월 16일에는 보름달이 나타납니다. 부활절은 3월 21일 또는 그 이후의 첫 번째 기독교 보름달 이후의 첫 번째 일요일입니다. (이 정의는 "이후"라는 단어의 역사적 의미와 모호함을 피하기 위해 "3월 21일 또는 그 이후"를 사용합니다. 현대 언어에서 이 문구는 단순히 "3월 20일 이후"를 의미합니다. "3월 21일 이후"의 정의는 출판 및 웹 기반 기사에서 "3월 21일 이후"로 잘못 축약되어 부활절 날짜가 잘못 표시되는 경우가 많습니다.) 예를 들어, 이 파스칼 보름달은 4월 16일입니다. 만약 부호 문자가 E라면 부활절은 4월 20일입니다.

"25"(xxv와 구별됨)라는 라벨은 다음과 같이 사용됩니다. 메토닉 사이클 내에서 11년 떨어져 있는 연도는 하루 차이가 나는 영향을 갖습니다. xxiv와 xxv라는 라벨이 나란히 적혀 있는 날짜로 시작하는 한 달은 29일 또는 30일입니다. 만약 24와 25가 둘 다 하나의 메토닉 주기 안에서 일어난다면, 이 2년 동안 새로운 위성과 완전 위성은 같은 날짜에 떨어질 것입니다. 이것은 실제 달의^[j] 경우에 가능하지만 도식적인 음력에서는 우아하지 않습니다. 날짜는 19년 후에만 반복되어야 합니다. 이를 방지하기 위해 25개의 반응이 있고 11보다 큰 황금 숫자가 있는 해에는 xxv가 아닌 25개의 레이블이 있는 날짜에 초승달이 해당합니다. 라벨 25와 xxv가 함께 있는 곳은 동일하므로 문제가 없습니다. 이것은 문제를 "25"와 "xxvi" 쌍으로 옮기지 않습니다. 왜냐하면 가장 초기의 26개의 반응은 주기의 23년에 나타날 것이기 때문인데, 이 주기는 19년 밖에 지속되지 않습니다: 그 사이에 새 위성이 다른 날짜에 떨어지도록 만드는 염류 루나(saltus lunae)가 있기 때문입니다.

그레고리력은 400년 동안 (항상 1세기에) 3번의 윤일을 감소시킴으로써 열대성 해에 대한 보정을 가지고 있습니다. 이것은 열대 해의 길이에 대한 보정이지만, 해와 달 사이의 메토닉 관계에는 영향을 미치지 않아야 합니다. 따라서 이 세기에 하나를 빼서 이를 보상(부분적으로 – epact 참조)합니다. 이것은 소위 태양 보정 또는 "태양 방정식"("정정"의 중세적 의미로 사용되는 방정식)입니다.

그러나 19년의 무보정 율리우스력은 235번의 런닝보다 조금 더 깁니다. 그 차이는 약 308년 중 하루, 즉 1년에 0.00324일로 누적됩니다. 한 주기에서 태양 보정으로 인해 에팩트는 평균 19 × 0.0075 = 0.1425만큼 감소하므로 주기는 235-0.1425/30 = 234.99525 달에 해당하는 반면 실제로 19 × 365.2425/29.5305889 ≈ 234.997261 시노딕 달이 있습니다. 19년 주기당 0.002011 시노드 월, 즉 연간 0.003126일의 차이는 때때로 달에 의한 효과 보정을 필요로 합니다. 그레고리력에서 이것은 2,500년(그레고리력)에 18번을 더함으로써 이루어지는데, (2,500 × 0.003126보다 약간 더 많음, 약 7.8) 항상 1세기에 이것은 소위 달 보정(역사적으로 "달 방정식"이라고 함)입니다. 첫 번째는 1800년에 적용되었고, 다음은 2100년에 적용되며, 새로운 주기를 시작하는 3900년에서 4300년 사이의 400년 간격을 제외하고는 300년마다 적용됩니다. 개혁 당시, 초승달이 뜨는 시기를 3일 동안 수정하기 위해 열흘을 건너뛰었는데도 7개씩 반응이 바뀌었습니다.^[45]

태양과 달의 보정은 서로 반대 방향으로 작용하며, 어떤 세기(예를 들어 1800년과 2100년)에는 서로 상쇄됩니다. 그 결과 그레고리력은 100년에서 300년의 기간 동안 유효한 유효표를 사용합니다. 위에 나열된 효과표는 1900년부터 2199년까지의 기간 동안 유효합니다.

아래에서 설명하는 바와 같이 부활절 날짜는 5,700,000년 이후에 반복되며, 이 기간 동안 기독교 월의 평균 길이는 2,081,882,250/70,499,183 ≈ 29.5305869일로 소수점 이후 6번째 그림의 현재 실제 평균 달의 길이(29,5305889 d: 음력 월#시노딕 월 참조)와 다릅니다. 이는 40,000년 동안 달의 위상에서 하루 미만의 오차에 해당하지만, 실제로 하루의 길이는 (시노딕 달의 길이와 마찬가지로) 변화하고 있으므로 이러한 기간 동안 시스템은 정확하지 않습니다. 하루 길이의 누적 변화에 대한 내용은 δT(timekeeping) 기사를 참조하십시오.

세부 사항

이 섹션은 확인을 위해 추가 인용이 필요합니다. 이 섹션의 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주시기 바랍니다. 미가공 재료는 도전하여 제거할 수 있습니다. 출처 찾기: "부활절 날짜" – 뉴스·신문·도서·학자·JSTOR(2020년 7월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

이 계산 방법에는 다음과 같은 몇 가지 미묘한 부분이 있습니다.

다른 음력 달에는 29일만 있으므로 하루에는 30개 중 2개의 효과 레이블이 할당되어야 합니다. 다른 것이 아닌 "xxv/25"라는 이팩트 레이블을 이동하는 이유는 다음과 같습니다. 디오니시우스가 페트로니우스에게 보낸 서간에 따르면, 에우세비우스의 권위에 관한 니케 공의회는 기독교 음력 1월(파스칼 달)은 3월 8일에서 4월 5일 사이에 시작되어야 하고, 14일은 3월 21일에서 4월 18일 사이에 있어야 한다고 규정했습니다. 따라서 (단) 29일의 기간에 걸쳐 있습니다. 3월 7일의 초승달은 3월 20일 14일째(보름달)인데, 이는 시기상조(3월 20일 이후가 아님)에 해당합니다. 따라서 "xxiv"의 효과가 있는 해는 3월 7일로 시작하는 음력이 30일이라면 4월 6일에 파스칼 초승달이 뜨는데, 이는 너무 늦습니다. 보름달은 4월 19일에 지고 부활절은 4월 26일에 늦어질 수 있습니다. 율리우스력에서 부활절의 가장 최근 날짜는 4월 25일이었고, 그레고리오 개혁은 그 한계를 유지했습니다. 따라서 파스칼 보름달은 늦어도 4월 18일에, 초승달은 4월 5일에 떨어져야 합니다. 따라서 4월 5일에는 이중 에팩트 레이블 "xxiv"와 "xxv"가 있어야 합니다. 그러면 위의 단락에서 설명한 바와 같이 "xxv"는 다르게 취급되어야 합니다.

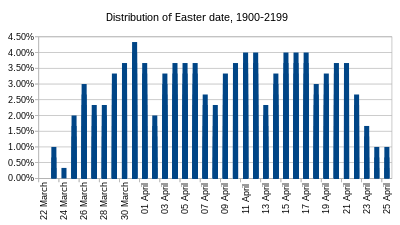
부활절 날짜의 빈도 분포는 잘못 정의되어 있습니다. 왜냐하면 100년에서 300년마다 황금 숫자에서 효과로 매핑이 변경되고 장기 빈도 분포는 수백만 년 동안만 유효하기 때문입니다(아래 참조). 반면, 시스템은 확실히 그렇게 오랫동안 사용되지 않을 것입니다. 1900년부터 2199년까지 유효한 현재 매핑은 매우 다양한 주파수의 부활절 날짜를 제공합니다. 3월 22일은 절대 일어날 수 없는 반면, 3월 31일은 이 300년의 기간 동안 13번 발생합니다.

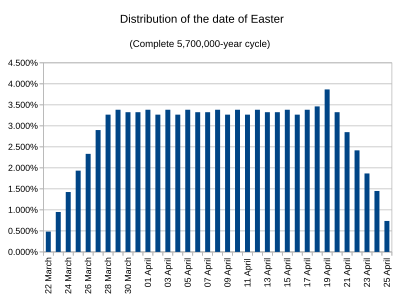
장기적으로, 즉 날짜가 반복되는 570만 년 전체 기간에 걸쳐 분포가 어떻게 되는지 질문한다면, 이 분포는 매우 간단하게 찾을 수 있으며 1900년부터 2199년까지의 기간의 분포, 심지어 개혁 이후 지금까지의 기간 동안의 분포와도 상당히 다릅니다. 특정 연도의 부활절 날짜는 해당 연도의 효과, 황금 숫자 및 일요일이 어느 날인지를 알려주는 지배적인 글자에만 의존합니다(더 정확하게는 윤년이 다른 2월 이후의 부분의 지배적인 글자는 1월과 2월의 글자). (앞에서 설명한 바와 같이 황금수는 epact가 25일 때만 중요합니다.) 우리가 특정 연도에서 3,230,000년 앞으로 간다면, 우리는 400년 그레고리안 주기의 같은 지점에서, 그리고 같은 황금수를 가진, 그러나 에팩트가 1만큼 증가한 1년을 발견합니다. 따라서 장기적으로는 30개의 모든 반응이 동일하게 나타날 가능성이 있습니다. 반면, 문자 A와 C가 있는 연도(연말)는 각각 14%, E와 F는 14.25%, B, D, G는 14.5%의 빈도로 모두 동일한 것은 아닙니다. 이는 epact 25와 관련된 복잡성을 고려하여 두 번째 그래프에 표시된 분포를 제공합니다. 4월 19일이 가장 일반적인 이유는 에픽이 25일 때 기독교 보름달은 4월 17일 또는 18일에 해당하고 에픽이 26일 또는 24일에도 해당하기 때문입니다. 부활절이 4월 19일이 되기 위해서는 4월 17일과 4월 18일을 포함하여 보름달이 떨어질 수 있는 7일이 있습니다(이것은 또한 4월 18일이 기독교 보름달의 가장 최근 날짜이기 때문에 기독교 보름달이 토요일에 떨어질 수 있는 가능한 가장 최근의 부활절 날짜이기도 합니다). 어느 부활절이 다음 날인지, 만약 기독교 보름달이 토요일에 있다면).^[45] 따라서 4월 19일은 그레고리력에서 부활절이 가장 많이 해당되는 날짜로, 1년 중 약 3.87%가 해당됩니다. 3월 22일이 0.48%^[47][45]로 가장 빈도가 적습니다.

음력 날짜와 태양력 날짜 사이의 관계는 태양력의 윤일 계획과 무관합니다. 기본적으로 그레고리력은 여전히 4년마다 윤일이 있는 율리우스력을 사용하기 때문에 19년의 메토닉 주기는 5,4개의 윤일이 있는 6,940일 또는 6,939일입니다. 이제 달의 주기는 19 × 354 + 19 × 11 = 6,935일밖에 되지 않습니다. 윤일을 에팩트 번호로 표시하고 세지 않고 다음 달 초승달이 윤일이 없는 것과 같은 달력 날짜에 놓이게 함으로써 현재의 윤일은 하루 연장되고 ^[k]235개의 윤일은 무려 19년을 포함합니다(1900년처럼 "태양 보정"이 포함되지 않는 한). 따라서 달력을 달과 동기화해야 하는 부담(intermedi 말기 정확도)은 태양력으로 옮겨지는데, 이는 모두 19 태양년 = 235 루네이션("lunar 보정"으로 보정되지 않으면 장기적인 부정확성이 발생함)이라는 가정 하에서 적절한 인터칼레이션 방식을 사용할 수 있습니다. 결과적으로, 달의 나이로 계산된 날짜가 하루 차이가 날 수도 있고, 윤일을 포함하는 달의 길이가 31일일일 수도 있는데, 이것은 진짜 달을 따라갔다면 결코 일어나지 않을 것입니다 (단기간의 부정확성). 이것은 태양력에 일반적으로 맞는 가격입니다.

그레고리안 부활절 주기를 1년 전체의 달력으로 사용하고 싶은 사람들의 관점에서 보면, 그레고리안 음력에는^[48] 몇 가지 결함이 있습니다(비록 파스칼 달과 부활절 날짜에는 영향을 미치지 않습니다).

1. 31일(그리고 때로는 28일)의 런닝이 발생합니다.
2. 만약 황금 숫자 19가 있는 해에 우연히 19화가 있다면, 마지막 기독교적인 초승달은 12월 2일이고, 다음 달은 1월 1일입니다. 하지만 새해가 시작되면 달맞이꽃이 다른 단위로 영향을 증가시켜 전날에 초승달이 떴어야 합니다. 그래서 초승달을 놓쳤습니다. 로마 미살 미살 로마누스 달력은 이를 고려하여 그 해의 12월 31일에 "xx" 대신 "19"를 부여하고, 그 날짜를 초승달로 만듭니다. 원래의 그레고리안 판탁이 시행되던 때(1690년에 마지막으로) 19년마다 일어났고, 그 다음은 8511년에 일어났습니다.
3. 만약 일년의 효과가 20이라면, 기독교적인 초승달은 12월 31일에 해당합니다. 만약 그 해가 100년 전에 해당한다면, 대부분의 경우 태양 보정은 새해의 영향을 1만큼 줄입니다. 그 결과로 나온 "*"는 또 다른 기독교적인 초승달이 1월 1일에 계산된다는 것을 의미합니다. 그래서 공식적으로는 하루의 런닝이 지났습니다. 다음은 4199-4200에서 발생합니다.
4. 다른 경계선 사례는 (훨씬 나중에) 발생하며, 규칙이 엄격하게 준수되고 이러한 사례를 특별하게 처리하지 않으면 1, 28, 59 또는 (아주 드물게) 58일 간격의 연속적인 초승달 날짜가 생성됩니다.

신중한 분석은 그레고리력에서 사용되고 수정되는 방식을 통해, 그 영향들은 사실 달맞이의 일부라는 것을 보여줍니다.30분의 1, 티티라고도 하며, 꼬박 하루를 보내는 것은 아닙니다. 토론은 epact를 참조하십시오.

태양과 달의 보정은 4×25 = 100세기 이후에 반복됩니다. 이 기간 동안 주어진 황금수에 대한 에팩트는 총 -1 × 3/4 × 100 + 1 × 8/25 × 100 = -43 ≡ 17 모드 30만큼 바뀝니다. 이것은 30개의 가능한 효과들 중 가장 중요하기 때문에, 효과 매핑들이 반복될 때까지 100 × 30 = 3,000 세기가 걸리고, 같은 황금 숫자로 반복될 때까지 3,000 × 19 = 57,000 세기가 걸립니다. 이 5.7 Myr 기간에 얼마나 많은 신월이 계산되는지는 분명하지 않습니다. Metonic 사이클은 최대 (5,700,000/19) × 235 = 70,500,000번의 런닝을 추가합니다. 그러나 효과에 대한 순 -43 × (5,700,000/10,000) 수정 사항이 있으며, 이를 30으로 나누면 총 70,499,183개의 실행에 대한 -817개의 실행 수정 사항이 추가됩니다. 이 숫자는 1837년 마그누스 게오르그 파우커에 의해 처음으로 도출된 것으로 보입니다.^[49] 1931년^[50] 항해 연감의 달력 장(p. 744)과 1992년 설명 부록(p. 582)에도 언급되어 있습니다.^[51][l] 따라서 그레고리안 부활절 날짜는 정확히 같은 순서로 5,700,000년, 70,499, 183 런닝 또는 2,081,882,250일 후에만 반복되며, 평균 런닝 길이는 2,081,882,250/70,499,183 = 29.53058690일입니다. 물론 달력은 열대성 년, 시노딕 월 및 일의 길이 변화로 인해 수천 년 후에 조정되어야 합니다.

그래서 그레고리력은 왜 태양력과 달의 보정이 따로 있고, 이 보정이 서로 취소되기도 하는지에 대한 의문이 제기됩니다. 릴리우스의 원래 작품은 보존되어 있지 않지만, 그의 제안은 1577년에 발행된 《전서》(Compendium Novae Ratis Restituendi Kalendarium)에 설명되어 있는데, 이 책에서 그가 고안한 교정 체계는 미래의 달력 개혁가들의 손에 완벽하게 유연한 도구가 되기 위한 것이었다고 설명되어 있습니다. 태양력과 음력이 상호간의 간섭없이 앞으로 교정될 수 있기 때문입니다.^[52] 이러한 유연성의 예는 코페르니쿠스의 이론에서 파생된 대체 삽입 시퀀스와 그에 상응하는 효과 수정을 통해 제공되었습니다.^[53]

태양력의 윤일에 대한 그레고리안 수정이 음력에 미치는 영향을 대략적으로 되돌리는 "태양 보정"은 그 효과를 율리우스력과 음력 사이의 원래 메토닉 관계로 되돌립니다. 이 기본적인 19년 주기에서 태양과 달 사이의 고유한 불일치는 3~4세기마다 그 영향에 대한 "달 보정"에 의해 보정됩니다. 그러나 정확한 수정은 율리우스 세기가 아닌 그레고리안 세기가 시작될 때 일어나므로 원래의 율리우스 메토닉 주기가 완전히 복원되지는 않습니다.

순 4 × 8 - 3 × 25 = 43 epact 감산은 10,000년에 걸쳐 균등하게 분배될 수 있지만(예: Lichtenberg 2003, pp. 45–76), 보정을 결합하면 두 사이클의 부정확성도 추가되므로 별도로 보정할 수 없습니다.

궤도의 본질적인 장기적 변화와 조석 감속으로 인해 지구의 회전이 느려지기 때문에 그레고리안 매개변수는 점점 더 쓸모가 없어집니다.

이것은 춘분의 날짜에 영향을 미치지만, 특히 평균 태양 시간으로 측정했을 때, 북반구(북반구 봄) 춘분 사이의 간격은 역사적인 시간 동안 상당히 안정적이었습니다.^[54][55]

또한 실제 보름달과 비교하여 그레고리안 방법으로 계산한 기독교 보름달의 표류는 예상보다 적게 영향을 받습니다. 왜냐하면 하루의 길이 증가는 거의 정확하게 한 달의 길이 증가로 보상되기 때문입니다. 조석 제동이 지구 자전의 각운동량을 달의 궤도 각운동량으로 전달하기 때문입니다.

기원전 4세기경 바빌로니아인들에 의해 확립된 평균 시노딕 월의 길이에 대한 프톨레마이오스 값은 29일 12시간 44분 3+1/3초 (키딘누 참조)이고, 현재 값은 0.46초 (신월 참조)입니다. 같은 역사적인 기간 동안 평균 열대 해의 길이는 약 10초 감소했습니다(모든 값은 태양 시간을 의미합니다).

영국 달력법과 공동기도서

위 표의 방법 부분은 16세기 후반 가톨릭 교회에 의해 부활절 일요일의 현재 날짜가 결정된 역사적 주장과 방법을 설명합니다. 율리우스력이 여전히 사용되고 있던 영국에서는 부활절 일요일이 1662년부터 1752년까지(이전 관행에 따라) 성공회 공동기도문(1662년 통일법에 의해 제정됨)의 간단한 날짜표에 의해 정의되었습니다. 이 표는 (부활절 부분에) 이미 알려진 것으로 추정되는 황금 숫자와 일요일 문자에 의해 직접 색인화되었습니다.

대영제국과 식민지들에게 부활절 일요일 날짜에 대한 새로운 결정은 그것의 부속서와 함께 현재 달력 (새로운 양식) 법 1750에 의해 정의되었습니다. 이 방법은 다른 곳에서 이미 사용 중인 그레고리안 규칙에 동의하는 날짜를 제공하기 위해 선택되었습니다. 그 행위는 공동 기도서에 넣어야 한다고 요구했고, 따라서 그것은 일반적인 성공회 규칙입니다. 원래의 행위는 1765년 영국 법령에서 볼 수 있습니다.^[56] 법률의 부속서에는 다음과 같은 정의가 포함되어 있습니다. "(나머지가 의존하는) 부활절은 항상 보름달 다음의 첫 일요일이거나 3월 21일 다음의 첫 일요일입니다. 그리고 만약 보름달이 일요일에 일어난다면 부활절은 그 다음 일요일입니다." 부속서는 이후 "파스칼 보름달"과 "기독교 보름달"이라는 용어를 사용하여 실제 보름달과 유사하다는 것을 분명히 합니다.

이 방법은 위에서 설명한 § 그레고리안 연산 체계의 개혁과는 상당히 다릅니다. 일반적인 해의 경우, 먼저 황금 숫자를 결정한 다음, 세 개의 표를 사용하여 일요일 문자, "사이퍼" 및 부활절 일요일 날짜가 뒤따르는 파스칼 보름달 날짜를 결정합니다. 효과가 명시적으로 나타나지 않습니다. 더 간단한 표는 사이퍼(태양 및 달 보정의 효과를 나타내는)가 변하지 않는 제한된 기간(예: 1900–2199) 동안 사용할 수 있습니다. 클라비우스의 세부 사항은 이 방법의 건설에 사용되었지만, 그 이후의 사용에는 아무런 역할도 하지 않습니다.^[57][58]

J. R. Stockton은 기도서와 달력법의 표를 추적할 수 있는 효율적인 컴퓨터 알고리즘을 도출한 것을 보여주고(표 사용법에 대한 설명이 임박했다는 가정하에), 일치하는 표를 계산하여 그 과정을 검증합니다.^[59]

율리우스력

그레고리력 개혁 이전에 서부 교회의 표준이었고 오늘날에도 여전히 대부분의 동부 기독교인들이 사용하는 기독교 보름달 날짜를 계산하는 방법은 율리우스력과 결합하여 19년 메토닉 주기의 수정되지 않은 반복을 사용했습니다. 위에서 살펴본 효과의 방법에 있어서는 절대 수정되지 않았던 효과 0으로 시작하는 단일 효과표를 효과적으로 사용하였습니다. 이 경우, 이 효과는 부활절로 허용되는 가장 빠른 날짜인 3월 22일에 계산되었습니다. 이는 19년마다 반복되므로, 3월 21일부터 4월 18일까지 포함하여 파스칼 보름달의 가능한 날짜는 19개뿐입니다.

그레고리력과 마찬가지로 수정 사항이 없기 때문에 기독교 보름달은 천년마다 진정한 보름달에서 3일 이상 떠납니다. 벌써 며칠이 지났습니다. 그 결과 동부교회는 서부교회보다 1주일 늦게 부활절을 기념하는 경우가 약 44%, 같은 날 약 30% 정도입니다. (동부 부활절은 율리우스력이 1900년에서 2099년 사이에 그레고리안보다 13일 늦기 때문에 때때로 4주 또는 5주 늦기도 합니다.) 그래서 그레고리안 파스칼 보름달은 율리우스력 3월 21일 이전에 있기도 합니다.

19년 주기의 1년의 수열을 황금수라고 합니다. 이 용어는 1200년 알렉산더 드 빌라 데이(Alexander de Villa Dei)의 컴퓨터 시 마사 콤포티(Massa Compoti)에서 처음 사용되었습니다. 후대의 서기관은 988년 플뢰리의 압보가 처음에 작성한 표에 황금 숫자를 추가했습니다.

1582년 그레고리력을 공표한 교황의 황소 성간(Inter gravissimas)에서 가톨릭 교회는 " ...에 의해 정해진 규칙에 따라 부활절을 기념하는 것"을 복원했다고 주장했습니다. 니케아의 위대한 에큐메니컬 평의회는 디오니시우스 엑시구우스(525)가 "부활절의 날짜를 정한다"고 한 거짓 주장에 근거를 두고 있습니다.^[60] 니케아 공의회에서 318명의 교회 신부들이 합의한 제안에 따라."^[61]

그러나 제1차 니케아 공의회(325)는 그 날짜를 결정하기 위한 명시적인 규칙을 제시하지 않았습니다. 그러나 "예전에 유대인의 관습을 따랐던 동방의 모든 우리 형제들은 앞으로 로마인들과 여러분 자신들 [알렉산드리아 교회], 그리고 처음부터 부활절을 지켜온 모든 사람들과 동시에 부활절이라는 가장 신성한 축제를 축하할 것입니다."라고만 썼습니다.^[62] 중세의 컴퓨터는 알렉산드리아 교회가 알렉산드리아 달력을 사용하여 4세기 첫 10년 동안 개발한 알렉산드리아 컴퓨터를 기반으로 합니다.^[63]

동로마제국은 연산을 율리우스력으로 변환한 후 380년 직후 이를 받아들였습니다.^[64] 로마는 6세기에서 9세기 사이에 그것을 받아들였습니다. 영국 섬들은 8세기 동안 몇몇 수도원들을 제외하고는 그것을 받아들였습니다.^{[citation needed]} 프랑크 왕국(스칸디나비아(파간), 영국 제도, 이베리아 반도, 이탈리아 남부를 제외한 서유럽 전체)은 8세기의 마지막 분기 동안 그것을 받아들였습니다.^{[citation needed]}

이를 받아들인 마지막 켈트족의 수도원인 이오나는 716년에 그렇게 했습니다.^{[citation needed]} 이를 받아들인 마지막 영국 수도원은 931년에 그렇게 했습니다.^{[citation needed]} 이 날짜들 이전에, 다른 방법들은 최대 5주 차이가 날 수 있는 부활절 일요일 날짜들을 만들었습니다.^{[citation needed]}

다음은 931년 이래 율리우스력의 모든 해에 대한 파스칼 보름달 날짜의 표입니다.

금으로 만든 번호	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
파스칼 보름달 날짜(줄리안)	5 4월	25 3월	13 4월	2 4월	22 3월	10 4월	30 3월	18 4월	7 4월	27 3월	15 4월	4 4월	24 3월	12 4월	1 4월	21 3월	9 4월	29 3월	17 4월
파스칼 보름달 1900~2099년 날짜, 그레고리력	18 4월	7 4월	26 4월	15 4월	4 4월	23 4월	12 4월	1 그럴지도 모른다	20 4월	9 4월	28 4월	17 4월	6 4월	25 4월	14 4월	3 4월	22 4월	11 4월	30 4월
파스칼 보름달 날짜, 서부, 1900-2199 (그레고리안)	14 4월	3 4월	23 3월	11 4월	31 3월	18 4월	8 4월	28 3월	16 4월	5 4월	25 3월	13 4월	2 4월	22 3월	10 4월	30 3월	17 4월	7 4월	27 3월

앞에서 언급했듯이, 이 파스칼 보름달은 서양보다 4일, 5일 또는 34일 늦으며, 천문학적인 보름달보다 약 3일 늦습니다. (예를 들어, 2015년 4월 월식은 그레고리력으로 4월 4일 또는 율리우스력으로 3월 22일이었습니다. 그러나 그 해의 파스칼 보름달(금 숫자 2)은 율리우스력으로 3월 25일이었습니다.) 달의 수정이 있을 때마다 서양과 동양의 교회 보름달 사이의 차이는 1씩 증가하므로 2100년부터 2399년까지 차이는 5일, 6일 또는 35일이 될 것입니다. 동방 파스칼 보름달의 그레고리력의 날짜 범위는 태양 보정이 있을 때마다 하루 늦게 이동하므로 2100년부터 2199년까지는 4월 5일부터 5월 9일까지입니다. 현재 동부활절이 서양보다 몇 주 늦은 경우, 황금 숫자 3, 8, 11, 14, 19의 한 주기당 5년이 있습니다. 이는 2200년에는 사이클당 6회(황금수 6회 추가)로 증가하고, 2300년에는 7회(황금수 17회 추가)로 증가한 후, 2400년에는 다시 6회(달 보정 및 태양 보정 없음)로 증가하고, 2500년에는 다시 7회, 2900년에는 8회(황금수 9회 추가)로 증가할 것입니다.^{[citation needed]}

다음 표를 사용한 계산 예제:

1573의 황금 숫자는 16(1573 + 1 = 1574; 1574 ÷ 19 = 82 나머지 16)입니다. 표에서 황금 숫자 16의 파스칼 보름달은 3월 21일입니다. 주표에서 보면 3월 21일은 토요일입니다. 부활절 일요일은 그 다음 일요일인 3월 22일입니다.

그래서 기독교 보름달의 주어진 날짜에 대해서는 7개의 부활절 날짜가 가능합니다. 일요일 문자의 주기는 7년 동안 반복되지 않습니다. 4년마다 윤일이 중단되기 때문에 달력에서 평일이 같은 방식으로 반복되는 전체 주기는 태양 주기인 4×7 = 28년입니다. 그래서 부활절 날짜는 4 × 7 × 19 = 532년 후에 같은 순서로 반복되었습니다. 이 파스칼 주기는 457년 로마에서 도입한 아키텐의 빅토리우스의 이름을 따서 빅토리아 주기라고도 불립니다.

알렉산드리아의 아니아누스가 5세기 초에 사용한 것으로 처음 알려져 있습니다. 또한 532년에 시작된 부활절 표를 준비한 디오니시우스 엑시구우스의 이름을 따서 때때로 디오니시우스 주기라고 잘못 불려왔습니다. 그는 분명히 자신이 묘사한 알렉산드리아의 계산기가 532년 주기를 가지고 있다는 것을 깨닫지 못했지만, 자신의 95년 표가 진정한 주기가 아니라는 것을 깨달았습니다. 베데(Bede) 수녀는 태양 주기를 처음으로 확인하고 메토닉 주기와 태양 주기로부터 파스칼 주기를 설명한 것으로 보입니다.

중세 서유럽에서, 위에 주어진 파스칼 보름달 (14 니산)의 날짜는 라틴어로 된 19줄의 반복적인 시의 도움으로 기억될 수 있었습니다:^[65][66]

노애 에이프릴리스	노르트키노	V
팔색조	의기소침한 마음을 품다	I
이두스 에이프릴리스	성병,	VI
사분면이 아닌	명색의 디콘디오	II
품목미정	양귀비인, 양귀비인,	V
quatuor idus	뿔제비갈매기	III
테르나스칼렌다스	적정제 세니,	VI
quatuor dene	사방팔방의	II
셉테나시두스	셉템프엘리트,	7세
세내칼렌대	분류 테르노,	III
데니셉테니스	동화되지 않는	I
Pridie nonas	포로쿼트니스,	II
무개목	탄저균이 아닌	7세
Pridie idus	판디투르키니,	V
에이프릴리스의 칼렌다스	실례를 범하다	I
듀오데나메크	쿼터니스를 하다,	II
표본 5중주	speramus duobus.	II
큰칼렌대	퀸크 코니쿤트,	V
퀸데 상수	tribus adaptis	III

각 선의 첫 번째 반선은 19년 주기의 각 연도에 대한 위 표에서 파스칼 보름달의 날짜를 알려줍니다. 두 번째 반선은 동시에 3월 24일부터 그해의 파스칼 보름달 날의 페리얼 규칙 또는 평일 변위를 제공합니다.^[67] 세 번째 열에는 페리얼 규칙이 로마 숫자로 반복됩니다.

"역동적인" 부활절 날짜

평균(북반구) 춘분점과 달의 위상에 대한 전산 계산의 근사치와 천문학적 원리에 따라 계산된 참값 사이의 불일치로 인해, 계산적인 계산에 따라 부활절 날짜와 교회의 아버지들에게 귀속된 원칙을 사용하여 천문학적인 방법으로 계산된 가상의 부활절 날짜 사이에 때때로 차이가 발생합니다. 이러한 불일치를 "역동적인" 부활절 날짜라고 합니다.^[68]

1474년의 칼렌다리움에서 레지오몬타누스는 1475년부터 1531년까지의 알폰신 표에 따라 뉘른베르크 경도에 대한 태양과 달의 모든 교차점의 정확한 시간을 계산했습니다. 그의 연구에서 그는 율리우스 연산기의 부활절이 천문학적인 New Moon을 사용하여 계산된 부활절과 일치하지 않는 30가지 사례를 표로 작성했습니다. 18건의 경우 날짜가 일주일, 7건은 35일, 5건은 28일 차이가 났습니다.^[68]

루트비히 랑게는 그레고리안 연산기를 사용하여 역설적인 부활절 날짜의 다양한 유형을 조사하고 분류했습니다.^[69] 천문학적 계산에 따른 최초의 설원 보름달이 일요일에 발생하고 연산기가 부활절과 같은 일요일을 제공하는 경우, 가상의 "천문학적으로" 정확한 부활절에 비해 기념되는 부활절은 일주일 전에 발생합니다. Lange는 이 경우를 부정적인 주간(hebdomadal) 역설(H-paradox)이라고 불렀습니다. 만약 천문학적 계산이 첫 번째 춘절 보름달에 대한 토요일을 제공하고 부활절이 바로 다음 주 일요일에 기념되지 않고 일주일 후에 계산에 따르면 부활절은 천문학적 결과에 비해 일주일 늦게 기념됩니다. 그는 그러한 경우를 긍정적인 주간(hebdomadal) 역설(H+ paradox)로 분류했습니다.^[69]

천문학 이론과 계산의 근사치와 관련하여 춘분에 따라 차이가 있다면 불일치는 더욱 큽니다. 만약 천문학적인 추분 보름달이 계산상의 추분 보름달보다 먼저 떨어진다면 부활절은 4주 혹은 심지어 5주나 더 늦게 기념될 것입니다. 이러한 경우를 랑게에 따르면 양의 분점 역설(A+ paradox)이라고 합니다. 역으로, 천문학적인 춘분 보름달보다 한 달 전에 춘분 보름달이 떨어질 때, 부활절은 4주 또는 5주 일찍 기념됩니다. 이러한 경우를 음의 분점 역설(A-paradox)이라고 합니다.^[69]

춘분과 보름달의 순서는 지리적 경도에 의존하지 않기 때문에 춘분 역설은 지구 전체에 항상 유효합니다. 대조적으로, 주간 역설은 대부분의 경우 국지적이고 지구의 일부에만 유효합니다. 왜냐하면 토요일과 일요일 사이의 낮의 변화는 지리적 경도에 따라 달라지기 때문입니다. 계산 계산은 베네치아의 경도에 유효한 천문표를 기반으로 하며, 랑게는 이를 그레고리안 경도라고 불렀습니다.^[69]

21세기와 22세기에^[69][70] 부정적인 주간 역설적 부활절 날짜는 2049년, 2076년, 2106년, 219년(글로벌), 2133년, 2147년, 2150년, 2170년, 2174년에 발생합니다. 긍정적인 주간 역설적 날짜는 2045년, 2069년, 2089년(글로벌), 2096년에 발생합니다. 2019년, 2038년, 2057년, 2076년, 2095년, 2114년, 2133년, 2152년, 2171년, 2190년의 양의 분점 역설적 날짜.^[70]

2076년과 2133년에는 이중 역설(양분점 주간과 음주 주간)이 발생합니다. 음의 추분 역설은 매우 희귀합니다. 부활절이 5주가 너무 빠른 2353년 4000년과 부활절이 4주가 너무 빠른 2372년까지 단 두 번만 발생합니다.^[70]

알고리즘

운영상의 주의사항

부활절 알고리즘을 표를 사용하지 않고 표현할 때는 단순한 기계식 계산기나 전자식 계산기를 사용하는 것과 호환되므로 정수 연산의 덧셈, 뺄셈, 곱셈, 나눗셈, 모듈로, 할당만 사용하는 것이 관례였습니다. 이러한 제한은 조건부 연산자 및 진술과 조회 테이블을 사용할 수 있는 컴퓨터 프로그래밍에는 바람직하지 않습니다. 3월 22일부터 56일까지를 하루와 달로 변환하는 방법을 쉽게 알 수 있습니다. 더 중요한 것은 이러한 조건을 사용하는 것이 그레고리안 계산의 핵심을 단순화한다는 것입니다.

가우스의 부활절 알고리즘

1800년 수학자 칼 프리드리히 가우스는 율리우스력이나 그레고리안 부활절 날짜를 계산하는 알고리즘을 제시했습니다.^[71][72] 그는 1816년 변수 p를 계산하기 위해 식을 수정했습니다.^[73] 1800년에 p = floor (k/3) = ⌊ k/3 ⌋를 잘못 기재하였습니다. 1807년, 그는 조건 (11M + 11) mod 30 < 19를 더 단순한 a > 10으로 대체했습니다. 1811년에 그는 자신의 알고리즘을 18세기와 19세기로만 한정하고, 명시된 상황에서 4월 26일은 항상 19일로, 4월 25일은 4월 18일로 대체된다고 말했습니다. 1816년, 그는 제자인 피터 폴 티텔이 원본에서 p가 틀렸다는 것을 지적해 준 것에 대해 감사를 표했습니다.^[74]

변수	표현	= 1777년	2024	2025
=	year mod 19	10	10	11
b =	year mod 4	1	0	1
c =	year mod 7	6	1	2
k =	year div 100 = ⌊ year/100 ⌋	17	20	20
p =	(13 + 8k) div 25 = ⌊13 + 8k/25⌋	5	6	6
q =	k div 4 = ⌊k/4⌋	4	5	5
M =	(15 − p + k − q) mod 30	23	24	24
N =	(4 + k − q) mod 7	3	5	5
율리우스력 M = 15, N = 6의 율리우스 부활절의 경우 (k, p, q는 불필요)
d =	(19a+M) mod 30	3	4	23
e =	(2b + 4c + 6d + N) mod 7	5	5	6
3월 부활절날 =	22 + d + e	30	31	51
4월 부활절날 =	d + d - 9	−1	0	20
	(11M + 11) mod 30	24	5	5
d = 28, e = 6, (11M + 11) mod 30 < 19인 경우 4월 25일을 4월 18일로 대체합니다.
d = 29이고 e = 6인 경우 4월 26일을 4월 19일로 대체합니다.

가우스의 부활절 알고리즘에 대한 분석은 두 부분으로 나뉩니다. 첫 번째 부분은 달 궤도의 대략적인 추적이고 두 번째 부분은 보름달 이후의 일요일을 얻기 위한 정확한 결정론적 상쇄입니다.

첫 번째 부분은 변수 d, (3월 22일부터) 보름 다음 날까지의 일수를 결정하는 것으로 구성됩니다. d에 대한 공식은 19a라는 용어를 포함하고 상수 M.a는 19년 달의 위상 주기에서 한 해의 위치이며, 가정에 따르면 지구에 대한 달의 움직임은 19년마다 반복됩니다. 옛날에는 음력 235년과 19년이 일치했는데, 이는 235년이 약 6939.6813일이고 19년이 평균 6939.6075일이기 때문에 현저하게 가깝습니다.

식 (19a + M) mod 30은 M이 세기별로 결정됨에 따라 각 세기 내에서 19년마다 반복됩니다. 19년 주기는 19a의 '19'와 아무런 관련이 없으며, 또 다른 '19'가 나타나는 것은 우연일 뿐입니다. 19a의 '19'는 역년과 음력의 정수 사이의 불일치를 수정하는 데서 비롯됩니다.

역년(leap이 아닌 해)은 365일이고, 음력의 정수를 갖는 달에 가장 가까운 달은 12 × 29.5 = 354일입니다. 그 차이는 11일인데, 다음 해 보름달이 뜨는 날을 11일 뒤로 옮겨서 수정해야 합니다. 그러나 모듈로 30 산술에서 11을 빼면 19를 더하는 것과 같으므로 각 연도에 19를 더하면 19a가 추가됩니다.

Min 19a + M은 각 세기가 시작될 때 올바른 출발점을 갖는 역할을 합니다. k가 100년마다 윤일을 억제하고, q가 400년마다 재설치하여 4년마다 윤일의 패턴에 (k - q)를 전체 억제 횟수로 산출하는 세기까지의 윤년 횟수로 계산하여 결정됩니다. 따라서 우리는 (k - q)를 추가하여 한 번도 발생하지 않은 윤일을 수정합니다. p는 달 궤도가 정수 용어로 완전히 설명될 수 없는 것을 수정합니다.

보름달이 부활절을 결정하는 데 고려되는 날짜의 범위는 3월 21일부터 4월 18일까지이며, 이는 29일 범위입니다. 그러나 변수 d와 상수 M의 mod 30 산술에서 둘 다 0~29 범위의 정수 값을 가질 수 있는 범위는 30입니다. 따라서 중요한 경우 조정이 이루어집니다. 일단 d가 결정되면, 이것은 보름달 다음 날의 날짜를 얻기 위해 3월 22일(가능한 가장 이른 보름달 다음 날, 춘분과 일치함)에 더하는 일수입니다.

그래서 부활절의 첫 번째 허용 날짜는 3월 22일 + d + 0입니다. 즉, 만약 보름달이 3월 21일 일요일에 있다면, 부활절은 7일 후에 기념되는 반면, 보름달이 3월 21일 토요일에 있다면, 부활절은 그 다음 3월 22일입니다.

두 번째 부분은 일요일에 도착하기 위해 오프셋된 날짜에 추가해야 하는 오프셋 날짜를 찾는 것입니다. 주에 7일이 있으므로 오프셋은 0~6 범위 내에 있어야 하며 모듈로 7 산술로 결정해야 합니다. e는 2b + 4c + 6d + N mod 7을 계산하여 결정됩니다. 이 상수들은 처음에는 이상하게 보일 수 있지만, 우리가 모드 7 산술 하에서 연산한다는 것을 기억한다면 꽤 쉽게 설명할 수 있습니다. 우선, 2b + 4c는 매년 평일이 미끄러진다는 사실을 확실히 처리합니다.

보통의 1년은 365일이지만 52 × 7 = 364이므로 52 주 전체는 하루를 너무 적게 구성합니다. 따라서 매년 연속적으로 평일은 "하루 앞으로 미끄러진다". 즉, 5월 6일이 1년 동안 수요일이었다면, 다음 해에는 목요일이다(윤년과는 무관함). b와 c가 모두 1년씩 증가합니다(모듈로 효과는 무시). 식 2b + 4c는 따라서 6만큼 증가합니다. 그러나 이것은 1 mod 7을 뺀 것과 같습니다.

1을 뺀다는 것은 정상적인 해에 정확히 필요한 것입니다. 평일이 하루 앞으로 미끄러지기 때문에 정확한 평일(즉, 일요일)에 도착하기 위해 하루 적게 보상해야 합니다. 윤년의 경우, b는 0이 되고 2b는 8이 아닌 0이 됩니다. 즉, mod 7에서는 1만큼의 또 다른 뺄셈, 즉 2만큼의 뺄셈이 됩니다. 즉, 그 해의 윤년 뒤 평일이 이틀 앞으로 미끄러지기 때문입니다.

6d라는 표현은 같은 방식으로 작동합니다. 어떤 숫자가 증가했다는 것은 보름달이 올해 며칠 후에 발생한다는 것을 의미하며, 따라서 우리는 며칠을 덜 보상해야 합니다. 6d를 더하면 원하는 연산인 d를 뺀 것과 같은 mod 7이 됩니다. 따라서 다시 모듈로 산술 아래에 덧셈을 하여 뺄셈을 합니다. 전체적으로 변수 e는 보름달 다음 날부터 가장 가까운 다음 일요일까지의 0일에서 6일 사이의 단계를 포함합니다. 상수 N은 각 세기에 대한 계산의 시작점을 제공하며 그레고리력이 구성되었을 때 1년 1월 1일이 암묵적으로 어디에 위치했는지에 따라 달라집니다.

d + e라는 표현은 3월 22일부터 4월 26일까지의 부활절 일요일을 가리키는 0~35 범위에서 오프셋을 산출할 수 있습니다. 역사적 호환성의 이유로, 35의 모든 오프셋과 34의 일부 오프셋은 7만큼 차감되어 일요일을 보름달의 날로 되돌립니다(사실상 -1의 음의 e를 사용함). 이것은 4월 26일이 결코 부활절 일요일이 아니라는 것과 4월 19일이 과도하게 대표된다는 것을 의미합니다. 후자의 수정은 역사적인 이유일 뿐 수학적 알고리즘과는 무관합니다. 오프셋 34는 19년 주기에서 d = 28 및 d = 29인 경우에만 조정됩니다.

역사적으로 1583년 이전에 가우스의 부활절 알고리즘을 사용한 것은 역사적으로 무의미합니다. 그레고리력은 그 해 이전에 부활절을 결정하는 데 사용되지 않았기 때문입니다. 다른 교회들이 부활절을 어떻게 정의할지 우리는 아무것도 모르기 때문에 알고리즘을 사용하는 것은 먼 미래에 의문입니다. 부활절 계산은 실제 천체의 움직임이나 논쟁의 여지가 없는 역사의 사실이 아니라 협약과 협약에 근거합니다.

익명 그레고리안 알고리즘

1876년 네이처 제출의 원형

배당금	나눗셈	몫	나머지
연도	19	—	a
연도	100	b	c
b	4	d	e
b + 8	25	f	—
b − f + 1	3	g	—
19a + b − d − g + 15	30	—	h
c	4	i	k
32 + 2e + 2i − h − k	7	—	l
a + 11h + 22l	451	m	—
h + l − 7m + 114	31	n	o

"뉴욕 특파원"은 그레고리안 부활절을 결정하는 이 알고리즘을 1876년 네이처지에 제출했습니다.^[74][75] 예를 들어, 1877년 사무엘 정육점에 의해,^[76] 1916년 아서 다우닝에 의해,^[77] 1922년 천문대에 H. 스펜서 존스에 의해,^[78] 1977년 영국 천문학 협회 저널에 의해,^[79] 1977년 노인 농부 연감에 의해, 1988년 피터 더펫 스미스가 당신의 계산기로 실용 천문학을, 1991년 장 미우스가 천문 알고리즘을 사용했습니다.^[80] Meeus 책 인용 때문에, 이것은 "Meeus/Jones/Butcher" 알고리즘이라고도 불립니다.

변수	표현	Y = 1961	2024	2025
=	Y모드 19	4	10	11
b =	⌊Y/ 100⌋	19	20	20
c =	Y모드 100	61	24	25
d =	⌊b/ 4⌋	4	5	5
e =	b 모드 4	3	0	0
f =	⌊b + 8/ 25⌋	1	1	1
g =	⌊b − f + 1/ 3⌋	6	6	6
h =	(19a + b − d − g + 15) mod 30	10	4	23
i =	⌊c/ 4⌋	15	6	6
k =	c mod 4	1	0	1
l =	(32 + 2e + 2i − h − k) mod 7	1	5	6
m =	⌊a + 11h + 22l/ 451⌋	0	0	0
	h + l − 7m + 114	125	123	143
n =	⌊h + l − 7m + 114/ 31⌋	4	3	4
o =	(h + l − 7m + 114) mod 31	1	30	19
그레고리안 부활절		1961년4월2일	2024년 3월 31일	2025년 4월 20일

이 알고리즘에서 변수 n은 한 해의 월(n = 3인 경우 3월 또는 n = 4인 경우 4월)을 나타내며, 월의 일은 (o + 1)로 구할 수 있습니다. 1961년 뉴 사이언티스트는 몇 가지 변경 사항을 포함하는 네이처 알고리즘 버전을 출판했습니다.^[81] 변수 g는 Gauss의 1816 보정을 사용하여 계산되었으며, 그 결과 변수 f가 제거되었습니다. 몇 가지 정리하면 변수 o(부활절 날짜를 얻으려면 추가해야 함)가 날짜를 직접 제공하는 변수 p로 대체됩니다.

변수	표현	Y = 1961	2024	2025
f	—	—	—
g =	⌊8b + 13/ 25⌋	6	6	6
m =	⌊a + 11h + 19l/ 433⌋	0	0	0
n =	⌊h + l − 7m + 90/ 25⌋	4	3	4
o	—	—	—	—
p =	(h + l - 7m + 33n + 19) 모드 32	2	31	20
그레고리안 부활절		1961년4월2일	2024년 3월 31일	2025년 4월 20일

미우스의 율리안 알고리즘

장 미우스(Jean Meeus)는 그의 책 천문 알고리즘(1991, p. 69)에서 율리우스력에 대한 율리우스력 부활절을 계산하는 다음과 같은 알고리즘을 제시합니다. 이는 현대 세계 대부분에서 시민 달력으로 사용되는 그레고리안 달력이 아닙니다. 후자의 달력에서 동방 정교회 부활절 날짜를 얻으려면 율리우스 날짜에 13일(1900년~2099년 기준)을 추가해야 하며, 마지막 행에 아래 날짜를 생성합니다.

동방 정교회 부활절 날짜

변수	표현	Y = 2008	2009	2010	2011	2016	2024	2025
=	Y모드 4	0	1	2	3	0	0	1
b =	Y모드 7	6	0	1	2	0	1	2
c =	Y모드 19	13	14	15	16	2	10	11
d =	(19c + 15) mod 30	22	11	0	19	23	25	14
e =	(2a + 4b − d + 34) mod 7	1	4	0	1	4	6	2
	d + d + 114	137	129	114	134	141	145	130
월 =	⌊d + d + 114/ 31⌋	4	4	3	4	4	4	4
day =	((d + e + 114) mod 31) + 1	14	6	22	11	18	22	7
부활절 (율리우스력)		2008년 4월 14일	2009년 4월 6일	2010년 3월 22일	2011년 4월 11일	2016년 4월 18일	2024년 4월 22일	2025년 4월 7일
부활절 (그레고리력)		2008년 4월 27일	2009년 4월 19일	2010년 4월 4일	2011년 4월 24일	2016년 5월 1일	2024년 5월 5일	2025년 4월 20일

참고 항목

• 크리스티안 젤러 – 독일의 수학자
• 십자가에 못박힌 어둠 – 어두워진 하늘의 기독교 복음서 에피소드
• 부활절 날짜 개편 – 축제 날짜 변경 제안

참고문헌

메모들

인용문

원천

추가읽기

외부 링크

• Excel 스프레드시트 공식 및 부활절 계산 함수
• 베데 전 6권(De Temporibus와 De Temporum Rationale 포함) 전집
• 1911년 가톨릭 백과사전에 수록된 사건들에 대한 소개
• 로돌프 오데트(Rodolphe Audette)가 프랑스어로 번역한 그레고리력 개혁의 원문(라틴어)
• 광범위한 서지학과 유용한 링크가 있는 부활절 계산기.
• 부활절 계산기가 있는 경도국(Bureau des Longitude)의 에페메리스(Ephemeris) 부지(325~2500 사이 유효)
• 홀거 외텔의 달력 페이지와 계산기
• Clive Feather의 한 페이지에 간단한 설명과 몇 개의 표, 그리고 또 다른 알고리즘이 포함되어 있습니다.
• (독일어로) 니콜라우스 A의 방대한 달력 사이트와 달력과 부활절 계산기. 2003년 9월 6일 Wayback Machine에 보관된 Bär
• 표 형식에 비해 절차가 개선된 그레고리안 태양력과 음력에 대한 설명, David Madore.
• 디오니시우스 엑시구우스의 부활절 표
• 영국 도서관의 원고에서 나온 손의 기억력 계산도
• St. Gallen, Stiftsbliothek, Codex Sangallensis 378 (11세기) p. 28. 노내 에이프릴리스 노룬트 키노스라는 시를 담고 있습니다.
• Ronald W. Mallen에 의해 326년부터 4099년까지의 부활절 날짜를 결정하는 단순화된 방법
• 달력 본문 (새로운 양식) 법률 1750, 현재까지 개정된 그레고리안 달력을 도입하는 영국 의회법 8599년까지의 부활절을 계산하기 위한 표가 들어 있습니다. 통과된 법과 대조합니다.
• Computuslat 라틴어 계산 알고리즘, 텍스트, 표, 다이어그램 및 달력을 포함하는 중세 원고의 데이터베이스입니다.