이차식
Quadratic formula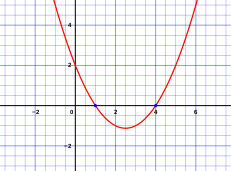
기본 대수학에서 이차 공식은 이차 방정식의 해를 설명하는 닫힌 형태의 표현입니다. 제곱을 완성하는 것과 같은 2차 방정식을 푸는 다른 방법들도 같은 해를 만듭니다.
+ + c = 0 + + c= 형식의 일반 이차 방정식이 주어졌을 때, 는 미지수를 나타내고 는 a b 알려진 실수 또는 복소수를 ≠ 0 a\n을 만족하는 x의값은 2차 공식을 사용하여 구할 수 있으며,
여기서 플러스 minus기호 {\pm은 방정식에 두 개의 근이 있음을 나타냅니다. 별도로 작성하면 다음과 같습니다.
수량 δ = - 4 \ = 2}-4ac}를 2차 방정식의 판별식이라고 합니다. If the coefficients , , and are real numbers then when , the equation has two distinct real roots; when , 방정식에는 하나의 반복되는 실근이 있으며,δ < 0 < 0}인 경우 방정식에는 서로 복소수인 두 개의 서로 다른 복소수 근이 있습니다.
기하학적으로 근은 포물선인 = + + c y = + 의 그래프가 x x 축을 가로지르는 값을 나타냅니다. 2차 공식은 포물선의 대칭축을 식별하는 데에도 사용될 수 있습니다.[4]
당량식
예를 들어, 2차 공식은 다양한 대체 표현식을 사용하여 동등하게 작성될 수 있습니다.
이는 먼저 2차 방정식을 로 나눈다음 x + + c = 0 }=로 만든 다음 새 계수를 표준 2차 공식에 대입하여 유도할 수 있습니다. 이 변형을 사용하면 중간 계산된 수량 style 를 재사용할 수있으므로 관련 산술을 약간 줄일 수 있습니다.
분모의 제곱근
Giulio Fagnano에 의해 처음 언급된 덜 알려진 이차 공식은 분모에 제곱근이 있는 방정식을 통해 동일한 근을 설명합니다(≠ 0 c\n로 가정). 0
여기서 플러스 기호 ∓ \mp}"는 표준 이차 공식과 같은 순서로 이차 방정식의 두 근을 나타냅니다.
이 변형은 농담 삼아 "citardauq" 공식("quadratic"을 거꾸로 표기함)이라고 불렀습니다.[6]
이가) + b - 4 또는- - 4 과(와) 반대 부호인 경우뺄셈이 치명적인 취소를 초래할 수 있습니다. 수치 계산에서 정확도가 떨어집니다. 의 부호에 따라 분자 또는 분모에 제곱근이 있는 이차 공식 버전 중 하나를 선택하면 이 문제를 피할 수 있습니다. 아래의 § 수치 계산을 참조하십시오.
이 버전의 이차 공식은 일반 함수의 근을 찾는 뮬러의 방법에 사용됩니다. Vieta의 공식중 하나인 ID x = / a } = 에서 표준 공식을 유도할 수 있습니다. 또는 원래 방정식 2+ b + = + =을 2 로 나누면 x- + - 1+ = + + a = 을 얻을 수 있습니다 표준 공식을 적용하여 근 - 1 을 찾은다음 역수를 사용하여 원래 방정식의 근 x 을 찾습니다.
파생상품
2차 공식을 도출하는 다양한 방법이 문헌에 나와 있습니다. 표준은 사각형 기법을 간단하게 적용한 것입니다.[7][8][9][10] 대안적인 방법은 때때로 정사각형을 완성하는 것보다 더 간단하며 수학의 다른 영역에 대한 흥미로운 통찰력을 제공할 수 있습니다.
사각형을 완성함으로써
먼저 2차 + + c = + + c=을(를 이(가 0이 아니기 때문에 허용되는 2차 나누는 것으로 시작합니다. 그런 다음 상수 항 / c를 빼서 오른쪽에 분리합니다.
좌변은 이제 광장을 완성하는 방법, 즉 준비가 되었습니다. k를 x + + 2 형식의 2차 다항식에 추가하여 제곱 이항 + 2 + = + 2 + k} 형식을 얻습니다.
좌변은 이제 완벽한 사각형이기 때문에 양변의 제곱근을 쉽게 구할 수 있습니다.
마지막으로 에서 b/ a 를 빼면 x을(를) 분리할 수 있습니다.
단축법
Instead of dividing by to isolate , it can be slightly simpler to multiply by instead to produce , which allows us to complete the square without need for fractions. 도출 단계는 다음과 같습니다.[11]
- 각 면에 를 곱합니다
- 양쪽에 2- b를 더하면 정사각형이 완성됩니다.
- 양쪽의 제곱근을 취합니다.
- x을(를) 분리합니다
따라서 2차 공식은 다음과 같이 유도됩니다.
정사각형을 완성하는 이 방법은 고대의 것으로 8-9세기 인도의 수학자 ś ī다라에게 알려졌습니다. 이 대체 방법은 제곱을 완성하는 현대 표준 방법과 비교하여 마지막 단계까지 분수를 피하므로 우변에서 공통 분모를 얻기 위해 3단계 이후에 재배열을 필요로 하지 않습니다.[11]
대체에 의한
또 다른 유도는 변수 변경을 사용하여 방정식을 u 및 일부 상수 의 관점에서 =± s u =\형식으로 입력합니다
= u- 2 x =를 2+ + c = + + c=에대입하여 제품을 확장하고 유사한 용어를 결합한 다음 를 해결하면 다음과 같은 이점이 있습니다
마지막으로, 양변의 제곱근을 취하고 u u에 대한 결과 표현식을 = - b x=에 다시 대입하면 익숙한 2차 공식이 나타납니다.
대수적 항등식을 이용하여
많은 역사 수학자들은 다음과 같은 방법을 사용했습니다.[13]
방정식 2+ b + c = 0 + + c= 의 근을 α 와 beta } 이라고 합니다. 미분은 차이의 제곱에 대한 항등식(복소수 두 개의 경우 valid)에서 시작되며, 이 항등식 중 양변에 제곱근을 취할 수 있습니다.
a≠ 0 a\n이므로 2차 방정식을 로 나누어 같은 근을 갖는 모닉 다항식을 얻을 수 있습니다. 즉,
이는 + =- beta =a}} 및 =c a {\beta ={ca}}를 의미합니다. 따라서 ID를 다시 작성할 수 있습니다.
그러므로,
및 각각에 대한 두 가지 가능성은 같은 두 근의 반대 순서이므로 이를 표준 이차 방정식으로 결합할 수 있습니다.
라그랑주 분해 기준
이차 공식을 도출하는 대안적인 방법은 갈루아 이론의 초기 부분인 [14]라그랑주 분해 방법을 사용하는 것입니다.[15] 이 방법은 입방 다항식과 4차 다항식의 근을 주기 위해 일반화될 수 있으며, 갈루아 이론으로 이어져 어느 정도의 대수 방정식의 해를 근의 대칭군인 갈루아 군으로 이해할 수 있습니다.
이 접근 방식은 원래 방정식을 대수적으로 재배열하는 것보다 근 자체에 초점을 맞춥니다. 모닉 이차 다항식 x + + + 가 주어지면 α 와 가 두 근이라고 가정합니다. 따라서 다항식 인자는 다음과 같습니다.
, p =- + p=-(\beta)} 및 =α β {\q=\\beta }를 의미합니다.
곱셈과 덧셈은 둘 다 가환이므로, exchanging the roots and will not change the coefficients and : one can say that and are symmetric polynomials in and . Specifically, they are the elementary symmetric polynomials – any symmetric polynomial in and can be expressed in terms of and instead.
다항식을 분석하고 푸는 갈루아 이론 접근법은 각각 근에서 대칭 함수인 다항식의 계수가 주어지면 대칭을 "깨어"서 근을 복구할 수 있는지 여부를 묻는 것입니다. 접근법을 사용하여 다항식을 해결하는 것은 n 대칭 그룹이라고 하며 차 다항식을 재정렬하는 방법과 관련이 있습니다 두 근을 재배열하는 유일한 방법은 두 근을 그대로 두거나 전치시키는 것이므로 이차 다항식을 푸는 것은 간단합니다.
루트 및 을를) 찾으려면 그 합과 차이를 고려합니다.
이들을 다항식의 라그랑주 분해능이라고 하며, 이로부터 근을 다음과 같이 복원할 수 있습니다.
Because is a symmetric function in and , it can be expressed in terms of and specifically as described above. 그러나α {\}과 }=\beta }을(를) 하면 역 - r = β - α {\-r_{2}=\alpha beta}이(가) 생성되므로 = -- β - beta }은(는) 대칭이 아닙니다. 2 는 대칭 다항식으로 표현할 수 없습니다. 그러나 =(- 2 }=(\beta2}}는 루트에서 대칭이며 p {\p}및 q {\q}로 표현할 수 있습니다. 구체적으로 =(- ) 2 =}=(\beta)^{2}={}
루트 및 beta }가 다음과 같이 복구됩니다.
단항 다항식의 2차 공식입니다.
= / p = = c/ q = c를 대입하면 임의의 2차 다항식에 대한 일반적인 식을 얻을 수 있습니다. 해결책은 다음과 같이 인식될 수 있습니다.
모닉 다항식의 꼭짓점과 판별점.
유사하지만 더 복잡한 방법은 3개의 분해능과 2차 방정식("해상 다항식")과 관련된 2 및 을 갖는입방 방정식에 대해 작동하며, 4차 방정식(도 4)에 대해서도 유사하게 풀 수 있습니다. 분해 다항식이 입방체이며, 이를 차례로 풀 수 있습니다.[14] 5차 방정식에 대한 동일한 방법은 24도 다항식을 생성하므로 문제가 단순화되지 않으며, 실제로 일반적인 5차 방정식의 해는 근만으로 표현할 수 없습니다.
수치계산
이상화된 실수의 산술을 사용하여 수행할 때는 2차 공식이 정확히 맞지만, 대신 근사 산술을 사용할 때는 소수점 이하 고정 소수점 이하로 수행하는 펜 앤 페이퍼 산술이나 컴퓨터에서 사용할 수 있는 부동 소수점 이진 산술 등이 사용될 때는 숫자 표현의 한계는 구현에 큰 주의를 기울이지 않으면 상당히 부정확한 결과를 초래할 수 있습니다. 구체적인 어려움으로는 b≈ ± δδ {\ \-b\{\인 경우 합 -± δ {\b\textstyle b approx \pm {\sqrt {\Delta}};δ을 하는 데 있어 치명적인 계산 = b 2 - 4 a c {\displaystyle \textstyle itself in cases where ; degeneration of the formula when , , or , 0 또는 무한으로 표현되며, 뿌리를 정확하게 표현할 수 있는 경우에도 매우 크거나 작은 수를 곱하거나 나눌 때 오버플로우 또는 언더플로우가 발생할 수 있습니다.[16][17]
≈ δ{\sqrt{\Delta}}: + δ {\-b+{\sqrt {\Delta}}의평가로 인해 치명적인 취소가 발생합니다. ≈때- b -δ {\ \ -Delta}}의 평가와 마찬가지로 -δ - δ {\approx -{\sqrt {\Delta}}의 평가도 수행됩니다. 표준 이차 공식을 사용할 때 두 근 중 하나를 계산할 때는 항상 덧셈이 필요합니다. 중간 계산의 작업 정밀도를 유지하는 반면 다른 루트를 계산하려면 뺄셈이 필요하므로 이를 손상시킵니다. 따라서 임의의 2차 방정식을 풀기 위해 표준 2차 공식을 순진하게 따르는 것은 결과가 항상 정확해야 한다면 용납할 수 없는 일반적인 전략입니다. 불행히도, 도입부 대수학 교과서는 일반적으로 학생들이 도입부 화학과 같은 다른 학교 과목에서 부정확한 결과를 얻도록 하지만 이 문제를 다루지 않습니다.[18]
예를 들어 포켓 계산기를 사용하여 - x+ = 0 x= 방정식을 풀려고 하면 2차 공식 = ± x=의 결과는 대략 다음과 같이 계산될 수 있습니다.
계산기가 각 단계에 대해 10진법의 정밀도를 사용했음에도 불구하고 거의 동일한 두 숫자의 차이를 계산한 결과 정확한 숫자가 4개뿐인 에 대한 결과가 나왔습니다.
정확한 결과를 복구하는 한 가지 방법은 ID 1 = / } = 를 사용하는 것입니다 이 에서 2 는 = 2/ x =} = 2} = {}로 계산할 수 있습니다., 전체 10자리 숫자에 맞는 것입니다. 분모에 제곱근이 있는 이차 공식 버전을 사용하여 근 중 하나를 계산하는 것도 다소 동등한 방법입니다(위 분모의 § 제곱근 참조).
2차 방정식 해법의 실제 컴퓨터 구현은 일반적으로 b의 부호에 따라 각 근에 사용할 공식을 선택합니다[20]
이러한 방법은 계산 b b 또는 에서 부동 소수점 지수의 오버플로 또는 언더플로를 방지하지못하므로 수치적으로 표현할 수 있는 루트가 정확하게 계산되지 않을 수 있습니다. 더 강력하지만 계산 비용이 많이 드는 전략은 =- c / \x =-u}(b{\ cbig /}\! a 2차 방정식을 다음과 같이 바꿉니다.
여기서 은(는) 부호 함수입니다. = / a d =\ c이라고 하면 이 방정식의 형식은 - 2 ± = 1 = 입니다 하나의 솔루션은 = + d ∓ 1{1} = ^{2mp 1}}이고 다른 은 u = ± / u 1 \{2} = 1u_{1}}입니다. 원래 방정식의 근은 =- (( / ) u 1 1} =}(b{\ cbig /}\! 및 - (( / a u 2 \{2}(b{\ cbig /}\![21][22]
추가적인 복잡성으로 제곱근의 비용과 추가 반올림은 제곱근을 2의 거듭제곱으로 근사화함으로써 방지할 수 있으며, 대표 가능한 근에 대한 지수 넘침은 여전히 방지할 수 있습니다.
역사적 발전
2차 방정식을 푸는 가장 초기의 방법은 기하학이었습니다. 바빌로니아 설형 정제는 2차 방정식을 푸는 데 축소 가능한 문제를 포함하고 있습니다.[23]: 34 이집트의 베를린 파피루스는 중왕국 (기원전 2050년~기원전 1650년)으로 거슬러 올라가 2항 이차방정식의 해를 담고 있습니다.[24]
그리스 수학자 유클리드 (기원전 300년경)는 영향력 있는 수학 논문인 그의 원소 2권에서 2차 방정식을 풀기 위해 기하학적 방법을 사용했습니다.[23]: 39 이차방정식에 대한 규칙은 기원전 200년경 중국의 수학 기술 9장에 등장합니다.[25][26] 그리스 수학자 디오판토스(서기 250년경)는 그의 연구 산술에서 유클리드의 기하학적 대수학보다 더 쉽게 대수적인 방법으로 2차 방정식을 풀었습니다.[23]: 39 그의 솔루션은 두 뿌리가 모두 양의 뿌리일 때도 하나의 뿌리만 제공합니다.[27]
인도의 수학자 브라마굽타(Brahmagupta)는 그의 논문 브라흐마스푸 ṭ 아시단타(Brahmasphu ṭasiddhannta, 서기 628년경)에 2차 공식을 포함시켰으며, 이 공식은 당시의 스타일로 단어로 쓰여졌습니다. 방정식 2+ b = c + =의 그의 해는 다음과 같습니다. "절대수에 [[제곱] 제곱수를 곱한 값에 [[제곱수]] 제곱수를 더하면, [[중간수]] 제곱수에서 [[중간수]] 제곱수를 뺀 값이 나옵니다. 제곱수의 2배로 나누면 값입니다."[30] 현대 표기법에서는 = ⋅ a + - )/ 2 a \= {+ b}}-b/}2a}로 표기할 수 있습니다. 인도의 수학자 ś르 ī다라(8~9세기)는 바카라 2세가 인용한 대수학 연구에서 2차 방정식을 푸는 유사한 알고리즘을 고안했습니다. 현대의 2차 공식은 인도에서 스리다라차랴의 공식이라고 불리기도 합니다.[citation needed]
9세기 페르시아의 수학자 무 ḥ마드 이븐 무샤 알콰리즈미 ī는 2차 방정식을 대수적으로 풀었습니다. 모든 경우를 다루는 이차 공식은 1594년 사이먼 스테빈에 의해 처음 얻어졌습니다.[32] 1637년 르네 데카르트는 오늘날 우리가 알고 있는 형태의 이차 공식의 특수한 경우를 포함하는 라 게오메트리를 출판했습니다.[33]
기하학적 유의성

- 뿌리와 y절편 빨간색
- 파란색으로 표시된 꼭짓점 및 대칭축
- 포커스와 디렉팅릭스를 핑크색으로
In terms of coordinate geometry, an axis-aligned parabola is a curve whose -coordinates are the graph of a second-degree polynomial, of the form , where , , c 는 ≠ a\n인 실수 값 상수 계수입니다. 0
기하학적으로 2차 공식은 그래프에서이 x 축과 교차하는 점 을 정의합니다. 나아가 두 용어로 구분할 수 있는데,
첫 번째 항은 대칭축인 x =- 2 x=-{\에 대해 설명합니다 두 번째 항인 2- / 는 루트가 대칭축에서 떨어진 거리를 제공합니다.
포물선의 이 x x축에 있는 경우 해당 방정식은 대칭선에 반복되는 하나의 루트를 가지며, 이 거리 항은 0입니다. 대수적으로 판별 2- = 0 b=
판별자가 양수이면 정점이 축에 있지 않고 포물선이 x축 방향으로 열려 두 번 교차하므로 해당 방정식은 두 개의 실근을 갖습니다. 판별자가 음수이면 포물선이 방향으로 열리고 x x축과 교차하지 않으며 방정식에는 실수 근이 없습니다. 이 경우 두 복소수 근은 대칭축의 부분이 x 값인 복소수 공액입니다.
치수분석
If the constants , , and/or are not unitless then the quantities and must have the same units, 2 및 b 용어가 단위에 대해 일치하기 때문입니다. 같은 논리로 계수 은는) 의 단위에 관계없이 와 동일한 단위를 가져야 합니다 이것은 물리량의 2차 표현식이 올바르게 설정되었는지 확인하는 강력한 도구가 될 수 있습니다.
참고 항목
참고문헌
- ^ Sterling, Mary Jane (2010), Algebra I For Dummies, Wiley Publishing, p. 219, ISBN 978-0-470-55964-2
- ^ "Discriminant review", Khan Academy, retrieved 2019-11-10
- ^ "Understanding the quadratic formula", Khan Academy, retrieved 2019-11-10
- ^ "Axis of Symmetry of a Parabola. How to find axis from equation or from a graph. To find the axis of symmetry ...", www.mathwarehouse.com, retrieved 2019-11-10
- ^ 구체적으로 Fagnano는 + = x + = 방정식으로 시작하여 다음과 같은 해를 구했습니다. (18세기에 정사각형 2 는 전통적으로 x 로 작성되었습니다.)
Fagnano, Giulio Carlo (1750). "Applicazione dell' algoritmo nuovo Alla resoluzione analitica dell' equazioni del secondo, del terzo, e del quarto grado" [Application of a new algorithm to the analytical resolution of equations of the second, third, and fourth degree]. Produzioni matematiche del conte Giulio Carlo di Fagnano, Marchese de' Toschi, e DiSant' Ononio (in Italian). Vol. 1. Pesaro: Gavelliana. Appendice seconda, eq. 6, p. 467. doi:10.3931/e-rara-8663.
- ^ Goff, Gerald K. (1976), "The Citardauq Formula", The Mathematics Teacher, 69 (7): 550–551, JSTOR 27960584
- ^ Rich, Barnett; Schmidt, Philip (2004), Schaum's Outline of Theory and Problems of Elementary Algebra, The McGraw–Hill Companies, Chapter 13 §4.4, p. 291, ISBN 0-07-141083-X
- ^ 리, 쉬후이. 중등학교 대수교사의 대수방정식 풀이 지도를 위한 수학적 지식 조사, p. 56 (ProQuest, 2007): "2차 공식은 2차 방정식을 푸는 가장 일반적인 방법이며, 제곱을 완성하는 또 다른 일반적인 방법에서 파생되었습니다."
- ^ 락스월드, 개리. 대학 대수학과 삼각법과 전미분학, p. 178(애디슨 웨슬리, 2002).
- ^ 베켄바흐, 에드윈 외. 현대 대학 대수학과 삼각법, p. 81 (웨즈워스 펍) 주식회사 1986).
- ^ a b Hoehn, Larry (1975), "A More Elegant Method of Deriving the Quadratic Formula", The Mathematics Teacher, 68 (5): 442–443, doi:10.5951/MT.68.5.0442, JSTOR 27960212
- ^ + = c + = 형식의 2차 방정식에서 시작하여Bháskara II(c. 1150)가 인용한 ś ī다라의 방법: "방정식의 양변에 [[계수]] 제곱의 4배와 같은 수를 곱하면, 그리고 그것들에 원래의 미지의 양의 제곱과 같은 숫자를 더합니다. [그러면 뿌리를 뽑아냅니다.]". Smith, David E. (1923), History of Mathematics, vol. 2, Boston: Ginn, p. 446
- ^ Debnath, Lokenath (2009), "The legacy of Leonhard Euler – a tricentennial tribute", International Journal of Mathematical Education in Science and Technology, 40 (3): 353–388, doi:10.1080/00207390802642237, S2CID 123048345
- ^ a b 클라크, A. (1984) 추상대수학의 요소. 택배회사 146쪽
- ^ Prasolov, Viktor; Solovyev, Yuri (1997), Elliptic functions and elliptic integrals, AMS Bookstore, p. 134, ISBN 978-0-8218-0587-9
- ^ Forsythe, George E. (1969). "Solving a Quadratic Equation on a Computer". The Mathematical Sciences: A Collection of Essays. MIT Press. pp. 138–152. ISBN 0-262-03026-8.
- ^ Goualard, Frédéric (2023). The Ins and Outs of Solving Quadratic Equations with Floating-Point Arithmetic (Technical report). University of Nantes. HAL hal-04116310.
- ^ Thompson, H. Bradford (1987). "Good numerical technique in chemistry: The quadratic equation". Journal of Chemical Education. 64 (12): 1009. doi:10.1021/ed064p1009.
- ^ 이 예는 다음과 같습니다. Henrici, Peter (1982). Essentials of Numerical Analysis with Pocket Calculator Demonstrations. New York: Wiley. p. 13.
- ^ Forsythe, George E. (1966), How Do You Solve a Quadratic Equation (PDF) (Tech report), Stanford University, STAN-CS-66-40 (AD639052)
- ^ Baker, Henry G. (1998). "You Could Learn a Lot from a Quadratic: Overloading Considered Harmful". SIGPLAN Notices. 33 (1): 30–38. doi:10.1145/609742.609746.
- ^ Mastronardi, Nicola; Van Dooren, Paul (2015). "Revisiting the stability of computing the roots of a quadratic polynomial". Electronic Transactions on Numerical Analysis. 44: 73–83.
- ^ a b c d Irving, Ron (2013), Beyond the Quadratic Formula, MAA, ISBN 978-0-88385-783-0
- ^ The Cambridge Ancient History Part 2 Early History of the Middle East, Cambridge University Press, 1971, p. 530, ISBN 978-0-521-07791-0
- ^ Aitken, Wayne, "A Chinese Classic: The Nine Chapters" (PDF), Mathematics Department, California State University, retrieved 28 April 2013
- ^ Smith, David Eugene (1958), History of Mathematics, Courier Dover Publications, p. 380, ISBN 978-0-486-20430-7
- ^ Smith, David Eugene (1958), History of Mathematics, Courier Dover Publications, p. 134, ISBN 0-486-20429-4
- ^ 브래들리, 마이클 수학의 탄생: 고대에서 1300까지, p. 86(Infobase Publishing 2006).
- ^ 매켄지, 다나. 제로 워드의 우주: 방정식을 통해 전해지는 수학 이야기, p. 61 (프린스턴 대학 출판부, 2012).
- ^ Stillwell, John (2004), Mathematics and Its History (2nd ed.), Springer, p. 87, ISBN 0-387-95336-1
- ^ O'Connor, John J.; Robertson, Edmund F. (2000), "Sridhara", MacTutor History of Mathematics Archive, University of St Andrews
- ^ Struik, D. J.; Stevin, Simon (1958), The Principal Works of Simon Stevin, Mathematics (PDF), vol. II–B, C. V. Swets & Zeitlinger, p. 470
- ^ Rene Descartes, The Geometry



















![{\displaystyle {\begin{aligned}ax^{2{\vphantom {|}}}+bx+c&=0\\[3mu]x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}&=0\\[3mu]x^{2}+{\frac {b}{a}}x&=-{\frac {c}{a}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ee3bcd259521d10a01fa06661e550f839e63a18)



![{\displaystyle {\begin{aligned}x^{2}+2\left({\frac {b}{2a}}\right)x+\left({\frac {b}{2a}}\right)^{2}&=-{\frac {c}{a}}+\left({\frac {b}{2a}}\right)^{2}\\[5mu]\left(x+{\frac {b}{2a}}\right)^{2}&={\frac {b^{2}-4ac}{4a^{2}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/251e2cac94767695459987bd7aceedff61332c2d)

 b
b




![{\displaystyle {\begin{aligned}ax^{2}+bx+c&=0\\[3mu]4a^{2}x^{2}+4abx+4ac&=0\\[3mu]4a^{2}x^{2}+4abx+b^{2}&=b^{2}-4ac\\[3mu](2ax+b)^{2}&=b^{2}-4ac\\[3mu]2ax+b&=\pm {\sqrt {b^{2}-4ac}}\\[5mu]x&={\dfrac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.{\vphantom {\bigg )}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e1afabdee7f5f3780c45f2b2e68cee7893e615e)
![{\displaystyle {\begin{aligned}a\left(u-{\frac {b}{2a}}\right)^{2}+b\left(u-{\frac {b}{2a}}\right)+c&=0\\[5mu]a\left(u^{2}-{\frac {b}{a}}u+{\frac {b^{2}}{4a^{2}}}\right)+b\left(u-{\frac {b}{2a}}\right)+c&=0\\[5mu]au^{2}-bu+{\frac {b^{2}}{4a}}+bu-{\frac {b^{2}}{2a}}+c&=0\\[5mu]au^{2}+{\frac {4ac-b^{2}}{4a}}&=0\\[5mu]u^{2}&={\frac {b^{2}-4ac}{4a^{2}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95c0b53b51f27df65795ba7f705239d8ba6ac4c5)
![{\displaystyle {\begin{aligned}(\alpha -\beta )^{2}&=(\alpha +\beta )^{2}-4\alpha \beta \\[3mu]\alpha -\beta &=\pm {\sqrt {(\alpha +\beta )^{2}-4\alpha \beta }}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eae1c159dbfd4254045c1c9fccaf2c4a036b247c)


![{\displaystyle {\begin{aligned}\alpha &={\tfrac {1}{2}}(\alpha +\beta )+{\tfrac {1}{2}}(\alpha -\beta )=-{\frac {b}{2a}}\pm {\frac {\sqrt {b^{2}-4ac}}{2a}},\\[10mu]\beta &={\tfrac {1}{2}}(\alpha +\beta )-{\tfrac {1}{2}}(\alpha -\beta )=-{\frac {b}{2a}}\mp {\frac {\sqrt {b^{2}-4ac}}{2a}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/124946f9e26759fdb460e7f8c59c0b748d3acc46)



![{\displaystyle {\begin{aligned}x^{2}+px+q&=(x-\alpha )(x-\beta )\\[3mu]&=x^{2}-(\alpha +\beta )x+\alpha \beta \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337581ff53e57e62cb7e0c2f4ed19fda8b4f0cd9)



























 (는)
(는) 










 전통적으로
전통적으로 


