격식어

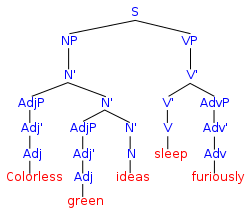
논리학, 수학, 컴퓨터 과학 그리고 언어학에서, 공식적인 언어는 알파벳으로부터 글자를 따왔고 특정한 규칙들에 따라 잘 형성된 단어들로 구성됩니다.

공식적인 언어의 알파벳은 ^[1]그 언어의 문자열로 연결되는 기호, 문자, 또는 토큰으로 구성됩니다.이 알파벳의 기호들로부터 연결된 각각의 문자열은 단어라고 불리고, 특정한 공식 언어에 속하는 단어들은 때때로 잘 형성된 단어 또는 잘 형성된 공식이라고 불립니다.형식 언어는 종종 정규 문법이나 문맥이 없는 문법과 같은 형식 문법에 의해 정의되는데, 이 문법은 그 형성 규칙으로 구성됩니다.

컴퓨터 과학에서, 공식 언어는 프로그래밍 언어의 문법과 언어의 단어가 의미나 의미론과 연관된 개념을 나타내는 자연 언어의 하위 집합의 형식화된 버전을 정의하는 데 기초로 사용됩니다.계산 복잡도 이론에서 의사결정 문제는 일반적으로 형식 언어로 정의되며, 복잡도 클래스는 계산 능력이 제한된 기계에 의해 파싱될 수 있는 형식 언어의 집합으로 정의됩니다.논리학과 수학의 기초에서 형식 언어는 공리계의 통사론을 나타내는 데 사용되며, 수학적 형식주의는 모든 수학이 이런 방식으로 형식 언어의 통사론적 조작으로 환원될 수 있다는 철학입니다.

형식 언어 이론 분야는 주로 그러한 언어들의 순수한 구문적 측면, 즉 내부 구조적 패턴을 연구합니다.형식 언어 이론은 자연 언어의 통사적 규칙성을 이해하는 방법으로서 언어학에서 비롯되었습니다.

역사

17세기에 고트프리트 라이프니츠는 그림문자를 사용한 보편적이고 형식적인 언어인 유니버설리스의 특징을 상상하고 묘사했습니다.이 기간 동안 칼 프리드리히 가우스는 가우스 ^[2]코드의 문제를 연구하기도 했습니다.

고틀롭 프레게는 베그리프스슈리프트(1879)에서 처음으로 서술된 주석 체계를 통해 라이프니츠의 아이디어를 실현하려고 시도했고, 그의 2권인 그룬드게세 데어 아리트메틱(1893/1903)^[3]에서 더 완전히 개발되었습니다.이것은 "순수한 ^[4]언어의 공식적인 언어"를 묘사했습니다.

20세기 전반에, 공식 언어와 관련된 몇 가지 발전이 이루어졌습니다.Axel Thue는 1906년에서 1914년 사이에 단어와 언어에 관한 4개의 논문을 발표했습니다.이 중 마지막은 에밀 포스트가 나중에 '화 시스템'이라고 명명한 것을 소개하고 결정할 수 없는 ^[5]문제의 초기 예를 제시했습니다.포스트는 나중에 이 논문을 1947년 "반군에 대한 단어 문제가 재귀적으로 불용성"^[6]이라는 증거의 기초로 사용했고, 나중에 공식 언어를 만들기 위한 표준 체계를 고안했습니다.

1907년 레오나르도 토레스 케베도는 빈에서 기계 도면(기계 장치)을 설명하는 데 공식적인 언어를 도입했습니다.그는 "기계의 설명을 용이하게 하기 위한 표기법과 기호 체계"^[7]를 출판했습니다.하인즈 제마넥은 ^[8]공작기계의 수치 제어를 위한 프로그래밍 언어에 해당한다고 평가했습니다.

Noam Chomsky는 Chomsky ^[9]hierarchy로 알려진 공식적이고 자연적인 언어의 추상적인 표현을 고안했습니다.1959년에 John Backus는 FORTRAN의 ^[10]작성에 대한 그의 연구에 이어 높은 수준의 프로그래밍 언어의 구문을 설명하기 위해 Backus-Naur 양식을 개발했습니다. Peter Naur는 ALGOL60 보고서의 비서/편집자였으며, 그는 Backus-Naur 양식을 사용하여 ALGOL60의 공식 부분을 설명했습니다.

알파벳 위의 단어들

공식 언어의 맥락에서 알파벳은 임의의 집합이 될 수 있지만, 일반적으로 단어의 일반적인 의미에서 알파벳을 사용하거나 ASCII 또는 유니코드와 같은 유한 문자 인코딩을 사용하는 것이 합리적입니다.알파벳의 요소들은 문자라고 불립니다.알파벳은 무한한 수의 ^{[note 1]}요소를 포함할 수 있지만 공식 언어 이론에서 대부분의 정의는 한정된 수의 요소를 가진 알파벳을 지정하고 대부분의 결과는 오직 요소에만 적용됩니다.

알파벳 위의 단어는 글자의 유한한 순서(즉, 문자열)일 수 있습니다.알파벳 σ 위에 있는 모든 단어의 집합은 보통 σ로 표시됩니다(클라인 별 사용).단어의 길이는 단어가 구성된 글자의 개수입니다.임의의 알파벳에 대해 길이 0의 단어는 단 하나뿐이며, 빈 단어는 종종 e, ε, λ 또는 심지어 λ로 표시됩니다.연접을 통해 두 단어를 결합하여 새로운 단어를 만들 수 있는데, 이 단어의 길이는 원래 단어의 길이의 합입니다.빈 단어와 단어를 연결한 결과가 원래 단어입니다.

일부 응용 프로그램, 특히 논리학에서 알파벳은 또한 어휘로 알려져 있고 단어는 공식 또는 문장으로 알려져 있습니다. 이것은 문자/단어 메타포를 깨고 단어/문장 메타포로 대체합니다.

정의.

알파벳 σ 위의 공식 언어 L은 σ의 부분 집합, 즉 해당 알파벳 위의 단어 집합입니다.때때로 단어 집합은 표현식으로 그룹화되는 반면 규칙과 제약은 '잘 형성된 표현식'을 만들기 위해 공식화될 수 있습니다.

보통 자연어를 다루지 않는 컴퓨터 과학과 수학에서 "공식"이라는 형용사는 종종 중복되는 것으로 생략됩니다.

형식 언어 이론이 일반적으로 일부 구문 규칙에 의해 설명되는 형식 언어와 관련이 있는 반면, "형식 언어"라는 개념의 실제 정의는 위와 같습니다: 주어진 알파벳으로 구성된 유한 길이의 문자열 집합, 그 이상도 이하도 아닙니다.실제로 일반 언어나 문맥이 없는 언어 등 규칙으로 설명할 수 있는 언어가 많습니다.형식문법의 개념은 통사적 규칙에 의해 설명되는 "언어"의 직관적 개념에 더 가까울 수 있습니다.정의를 남용함으로써, 특정한 형식 언어는 종종 그것을 설명하는 형식적인 문법을 갖춘 것으로 생각됩니다.

예

다음 규칙은 알파벳 σ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, =}에 대한 공식 $언어$ L을 설명합니다.

"+" 또는 "="를 포함하지 않고 "0"으로 시작하지 않는 비어 있지 않은 문자열은 모두 L에 $있습니다$ .
문자열 "0"은 L $안$ 에 있습니다.
"="를 포함하는 문자열은 "="가 하나만 있는 경우에만 LI에 $있으며$ L의 $유효$ 한 문자열 두 개를 구분합니다.
"+"를 포함하지만 "="를 포함하지 않는 문자열은 LIf에 $있으며$ 문자열의 모든 "+"가 $L$ 의 유효한 문자열 두 개를 구분하는 경우에만 해당합니다.
이전 규칙에서 암시한 문자열 외에 L에 $있는$ 문자열은 없습니다.

이러한 규칙에서 문자열 "23+4=555"는 L에 $있지만$ "=234=+"는 L에 있지 않습니다.이 공식 언어는 자연수, 잘 형성된 덧셈, 잘 형성된 덧셈 등을 표현하지만, 그것은 그것들이 무엇을 의미하는지(의미론)가 아니라 그것들이 어떤 모습인지(그들의 구문)만을 표현합니다.예를 들어, 이러한 규칙 어디에도 "0"은 숫자 0을 의미하고, "+"는 덧셈을 의미하며, "23+4=555"는 거짓을 의미하는 표시가 없습니다.

시공

유한한 언어의 경우, 모든 잘 형성된 단어를 명시적으로 열거할 수 있습니다.예를 들어, L $언어$ 를 L = {a, b, ab, cba} $로만$ 설명할 수 있습니다.이 구조의 퇴화된 경우는 빈 언어로, 단어가 전혀 포함되어 있지 않습니다( $L$ = ∅).

그러나 σ = {a, b}와 같은 유한한 (공백이 아닌) 알파벳 위에서도 무한히 많은 유한 길이의 단어가 표현될 수 있습니다: "a", "abb", "ababba", "aaabbbbaab", "aaabbbbaab", ...따라서 형식 언어는 일반적으로 무한하며, 무한한 형식 언어를 설명하는 것은 L = {a, b, ab, cba}를 쓰는 것만큼 간단하지 않습니다.공식 언어의 몇 가지 예는 다음과 같습니다.

$L$ $=$ $σ$ , $σ$ 위의 모든 단어의 집합;
$L$ $=$ {a} $=$ {a}, 여기서 n은 자연수 범위이고 "a"는 n번 반복되는 "a"를 의미합니다(이것은 기호 "a"로만 구성된 단어 집합입니다).
주어진 프로그래밍 언어의 구문적으로 올바른 프로그램 집합(문법은 대개 문맥이 없는 문법으로 정의됨).
특정 튜링 기계가 정지하는 입력 집합; 또는
영숫자 ASC의 최대 문자열 집합이 선에 있는 II 문자, 즉,
{the, set, of, maximal, 문자열, 영숫자, ASCII, 문자, on, this, line, i, e} 집합.

언어 사양 형식주의

공식 언어는 여러 학문 분야에서 도구로 사용됩니다.그러나 형식 언어 이론은 특정 언어에 관심을 갖는 경우가 거의 없으며(예를 제외하고), 주로 언어를 설명하기 위한 다양한 유형의 형식주의 연구에 관심을 갖습니다.예를 들어, 언어는 다음과 같이 주어질 수 있습니다.

어떤 형식적인 문법에 의해 생성된 문자열.
특정 정규 표현식으로 설명되거나 일치하는 문자열.
튜링 기계나 유한 상태 오토마타와 같은 일부 오토마타가 수용하는 문자열;
일부 의사결정 절차(관련된 YES/NO 질문의 순서를 묻는 알고리즘)가 YES라는 대답을 생성하는 문자열입니다.

이와 같은 형식주의에 대해 묻는 대표적인 질문은 다음과 같습니다.

그들의 표현력은 무엇일까요? (형식주의 X가 형식주의 Y가 묘사할 수 있는 모든 언어를 묘사할 수 있을까요?다른 언어를 묘사할 수 있습니까?)
인지도가 얼마나 됩니까?(어떤 단어가 형식주의 X에 의해 기술된 언어에 속하는지 판단하는 것이 얼마나 어려운가요?)
그들의 비교 가능성은 얼마나 됩니까?(하나는 형식주의 X에서 설명되고 하나는 형식주의 Y에서 설명되는 두 언어, 또는 다시 X에서 설명되는 두 언어가 실제로 동일한 언어인지 여부를 결정하는 것은 얼마나 어려운가?)

놀랍게도, 이러한 의사결정 문제에 대한 대답은 "전혀 할 수 없다"거나 "엄청나게 비싸다"(얼마나 비싼지의 특성이 있음)는 것입니다.따라서 형식 언어 이론은 계산 가능성 이론과 복잡도 이론의 주요 응용 분야입니다.형식 언어는 생성 문법의 표현력과 인식 오토마톤의 복잡성에 따라 촘스키 계층에서 분류될 수 있습니다.문맥이 없는 문법과 일반 문법은 표현력과 구문 분석의 용이성 사이에서 좋은 절충점을 제공하며, 실용적인 응용 분야에서 널리 사용됩니다.

언어에 대한 연산

언어에 대한 특정 작업은 일반적입니다.여기에는 결합, 교차, 보 등의 표준 집합 연산이 포함됩니다.연산의 또 다른 클래스는 문자열 연산의 요소별 적용입니다.

예: $L_{1}$ {\ $displaystyle$ L_ ${1}$ 과 $L_{1}$ $L_{2}$ {\ $displaystyle$ L_ ${2}$ 이 $L_{2}$ (가) 일부 공통 알파벳 ${\displaystyle \Sigma$ 를 넘는 언어라고 $L_{1}$ 합니다.

$L_{1}\cdot L_{2}$ $L_{1}\cdot L_{2}$ 1 ⋅ $L_{1}\cdot L_{2}$ 2 $L_{1}\cdot L_{2}$ {\ $displaystyle$ L_ ${1}\cdot$ L_ ${2}}$ 는 $w$ $L_{1}$ ${\displaystyle$ vw} $형식의$ 모든 $vw$ 로 $L_{1}$ 됩니다. 여기서 $v$ ${\displaystyle$ v}는L 1 ${\$ $displaystyle$ L_{ $1}$ 의 문자열이고 w ${\$ $displaystyle$ w $}$ 는 L 2 {\ $displaystyle$ L_ ${2$ 의 문자열입니다.
$L_{1}$ ${\displaystyle$ L_ ${1}}$ 와 $L_{2}$ {\ $displaystyle$ L_ ${2$ $}$ 의 $L_{1}\cap L_{2}$ $L_{1}\cap L_{2}$ ∩ $L_{1}\cap L_{2}$ {\ $displaystyle$ L_ ${1}\cap$ L_ ${2$ $}$ 는 두 언어에 포함된 모든 문자열로 구성됩니다.
${\displaystyle \Sigma$ }에 $\Sigma$ $\Sigma$ 대한 $L_{1}$ ${\$ L_ ${1}$ 의 $L_{1}$ $L_{1}$ $\neg L_{1}$ ${\$ 는 $\neg L_{1}$ $L_{1}$ ${\$ 에 $L_{1}$ $\Sigma$ 위의 $\Sigma$ 모든 문자열로 구성됩니다.
클라인 별: 원래 언어에서 0개 이상의 단어가 연결된 모든 단어로 구성된 언어;
반전:
- ε를 빈 단어라고 하고, ε $\varepsilon ^{R}=\varepsilon$ = $\varepsilon ^{R}=\varepsilon$ ε ${\displaystyle \varepsilon ^{R$ }=\ $varepsilon$ $\varepsilon ^{R}=\varepsilon$ 및
- 비어 있지 않은 각 $w=\sigma _{1}\cdots \sigma _{n}$ w = σ 1 ⋯ n $w=\sigma _{1}\cdots \sigma _{n}$ σ {\ $displaystyle$ w =\ $lot$ _ ${1}\cdots$ \lots $_{n}}$ (여기서 σ 1 $\sigma _{1},\ldots ,\sigma _{n}$ $\sigma _{1},\ldots ,\sigma _{n}$ σ n $\sigma _{1},\ldots ,\sigma _{n}$ {\ $displaystyle \lots$ _ ${1},\ldots,\lots$ _ ${n}$ 는 일부 알파벳의 요소), $w^{R}=\sigma _{n}\cdots \sigma _{1}$ $w^{R}=\sigma _{n}\cdots \sigma _{1}$ = σ n σ ⋯ 1 $w^{R}=\sigma _{n}\cdots \sigma _{1}$ {\ $displaystyle$ w $^{R$ }=\ $sigma$ _ ${n}\cdots \lots$ _ ${1$
- 형식 언어 $L$ ${\displaystyle$ L $L$ 의 경우 $L^{R}=\{w^{R}\mid w\in L\}$ = { $L^{R}=\{w^{R}\mid w\in L\}$ R $L^{R}=\{w^{R}\mid w\in L\}$ ∣ $L^{R}=\{w^{R}\mid w\in L\}$ ∈ $L^{R}=\{w^{R}\mid w\in L\}$ } ${\displaystyle$ L $^{R$ }=\{ $w^{R}\mid$ w $\in$ L $L^{R}=\{w^{R}\mid w\in L\}$
끈 동형 사상

이러한 문자열 연산은 언어 클래스의 닫힘 속성을 조사하는 데 사용됩니다.언어 클래스는 클래스의 언어에 적용된 연산이 항상 같은 클래스의 언어를 다시 생성할 때 특정 연산 하에서 닫힙니다.예를 들어, 문맥이 없는 언어는 결합, 연접, 정규 언어와의 교집합에서는 닫히지만 교집합이나 보집합에서는 닫히지 않는 것으로 알려져 있습니다.3개의 언어와 추상적 언어군의 이론은 ^[11]그들 자신의 권리에서 언어군의 가장 일반적인 폐쇄성을 연구합니다.

L_{1}

패밀리의 닫힘 속성(

L1

{\

displaystyle

L_{2}

{

1

}} Op

L2

{\displaystyle

L_{2}

L_

{

2},

L1 {\

displaystyle

{

}} 및

L2

{\displaystyle

L_{2}

L_

{2}}

가 모두 열에 의해 지정된 언어 패밀리에 있습니다.)

작동		규칙적인.	DCFL	CFL	IND	CSL	재귀적	RE
유니언	$L_{1}\cup L_{2}=\{w\mid w\in L_{1}\lor w\in L_{2}\$	네.	아니요.	네.	네.	네.	네.	네.
교차로	$L_{1}\cap L_{2}=\{w\mid w\in L_{1}\land w\in L_{2}\$	네.	아니요.	아니요.	아니요.	네.	네.	네.
보배	$\neg L_{1}=\{w\mid w\not \in L_{1}\$	네.	네.	아니요.	아니요.	네.	네.	아니요.
연접	$L_{1}\cdot L_{2}=\{wz\mid w\in L_{1}\land z\in L_{2}\$	네.	아니요.	네.	네.	네.	네.	네.
클린 스타	$L_{1}^{}=\{\varepsilon \}\cup \{wz\mid w\in L_{1}\land z\in L_{1}^{}\$	네.	아니요.	네.	네.	네.	네.	네.
( 문자열) $동형$ h ${\displaystyle$ h $}$	$h(L_{1})=\{h(w)\mid w\in L_{1}\$	네.	아니요.	네.	네.	아니요.	아니요.	네.
ε-free ( 문자열) $h$ h ${\displaystyle$ h $}$	$h(L_{1})=\{h(w)\mid w\in L_{1}\$	네.	아니요.	네.	네.	네.	네.	네.
대체 φ $\varphi$	$\varphi (L_{1})=\bigcup _{\cdots _{1}\cdots \cdots _{n}\in L_{1}}\varphi (\cdots _{1})\cdots \cdots \cdots \varphi (\cdot _{n})$	네.	아니요.	네.	네.	네.	아니요.	네.
역동형 $h^{-1}$ - 1 $h^{-1}$ {\ $displaystyle$ h $^{-1}}$	$h^{-1}(L_{1})=\bigcup _{w\in L_{1}}h^{-1}(w)$	네.	네.	네.	네.	네.	네.	네.
리버스	$L^{R}=\{w^{R}\mid w\in L\$	네.	아니요.	네.	네.	네.	네.	네.
일반 $언어$ R과의 $교집합$ {\ $displaystyle$ R $}$	$L\cap R=\{w\mid w\in L\land w\in R$	네.	네.	네.	네.	네.	네.	네.

적용들

프로그래밍 언어

컴파일러는 일반적으로 두 개의 다른 구성 요소를 갖습니다.때때로 와 같은 도구에 의해 생성되는 어휘 분석기는 프로그래밍 언어 문법의 토큰(예: 식별자 또는 키워드, 숫자 및 문자열 리터럴, 구두점 및 연산자 기호)을 식별합니다. 이들은 그 자체로 일반적으로 정규 표현식을 통해 더 간단한 공식 언어로 지정됩니다.가장 기본적인 개념적 수준에서 파서는 때때로 파서 발생기와 같은 파서 발생기에 의해 생성됩니다.yacc, 소스 프로그램이 구문적으로 유효한지, 즉 컴파일러가 작성된 프로그래밍 언어 문법과 관련하여 잘 형성되었는지 여부를 결정하려고 시도합니다.

물론 컴파일러는 단순히 소스 코드를 구문 분석하는 것 이상의 작업을 수행합니다. 일반적으로 이를 실행 가능한 형식으로 변환합니다.이 때문에 파서는 일반적으로 추상 구문 트리인 예/아니오 답변 이상을 출력합니다.이는 컴파일러의 후속 단계에서 하드웨어에서 직접 실행되는 시스템 코드 또는 가상 시스템을 실행해야 하는 일부 중간 코드를 포함하는 실행 파일을 생성하는 데 사용됩니다.

형식적인 이론, 체계, 증명

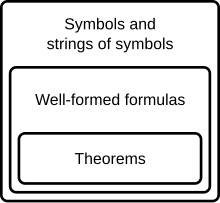
수학적 논리학에서 형식 이론은 형식적인 언어로 표현되는 문장의 집합입니다.

형식적 체계는 연역적 장치(연역적 체계라고도 함)와 함께 형식 언어로 구성됩니다.연역 장치는 유효한 추론 규칙 또는 공리 집합으로 해석될 수 있는 변환 규칙 집합으로 구성되거나 둘 다 가질 수 있습니다.공식 시스템은 하나 이상의 다른 식에서 하나의 식을 유도하는 데 사용됩니다.공식적인 언어는 공식과 동일시될 수 있지만, 공식적인 체계는 그것의 정리로 동일시될 수 없습니다.두 형식 ${\mathcal {FS}}$ ${\mathcal {FS}}$ S ${\mathcal {FS}}$ {\ $displaystyle$ {\ $mathcal {FS}}$ ${\mathcal {FS'}}$ F $'$ {\ $displaystyle$ {\ $mathcal {FS'}}$ 는 ${\mathcal {FS}}$ ${\mathcal {FS'}}$ 모두 동일한 정리를 갖지만 몇 가지 중요한 증명 이론적 방식으로 다를 수 있습니다(예를 들어 공식 A는 공식 B의 구문 결과일 수 있지만 다른 것은 아닙니다).

형식적 증명 또는 파생은 추론 규칙에 의해 순서의 앞의 공식들로부터 따르거나 공리인 (문장이나 명제로 해석될 수 있는) 잘 형성된 공식들의 유한한 순서입니다.수열의 마지막 문장은 형식 체계의 정리입니다.형식적 증명은 그들의 정리가 참된 명제로 해석될 수 있기 때문에 유용합니다.

해석 및 모델

형식 언어는 본질적으로 완전히 통사적이지만 언어의 요소에 의미를 부여하는 의미론이 주어질 수 있습니다.예를 들어, 수학적 논리학에서 특정 논리의 가능한 공식들의 집합은 형식 언어이고 해석은 각각의 공식에 의미를 부여합니다. 보통 진리값입니다.

형식 언어의 해석에 대한 연구는 형식 의미론이라고 불립니다.수학적 논리학에서, 이것은 종종 모델 이론의 관점에서 행해집니다.모형 이론에서, 공식에서 발생하는 용어들은 수학적 구조 내의 대상으로 해석되며, 고정된 구성 해석 규칙은 공식의 참값이 어떻게 그 용어들의 해석으로부터 도출될 수 있는지를 결정합니다; 공식의 모형은 공식이 참이 되도록 용어들을 해석하는 것입니다.

참고 항목

메모들

^ 예를 들어, 1차 논리는 종종 ¬, ∀, ∧, and, 괄호와 같은 기호 외에도 변수 역할을 하는 무한히 많은 요소 x, x, x, …를 포함하는 알파벳을 사용하여 표현됩니다.

참고문헌

인용문

^ 예를 들어,Reghizzi, Stefano Crespi (2009). Formal Languages and Compilation. Texts in Computer Science. Springer. p. 8. Bibcode:2009flc..book.....C. ISBN 9781848820500. An alphabet is a finite set
^ "In the prehistory of formal language theory: Gauss Languages". January 1992. Retrieved 30 April 2021.
^ "Gottlob Frege". 5 December 2019. Retrieved 30 April 2021.
^ Martin Davis (1995). "Influences of Mathematical Logic on Computer Science". In Rolf Herken (ed.). The universal Turing machine: a half-century survey. Springer. p. 290. ISBN 978-3-211-82637-9.
^ "Thue's 1914 paper: a translation" (PDF). 28 August 2013. Archived (PDF) from the original on 30 April 2021. Retrieved 30 April 2021.
^ "Emil Leon Post". September 2001. Retrieved 30 April 2021.
^ 토레스 케베도, 레오나르도Sobrun Sistema de notaciones y symbolos destinados a facilityitar la descripción de las máquinas, (pdf), pp. 25-30, Revista de Obras Publicas, 1907년 1월 17일.
^ Bruderer, Herbert (2021). "The Global Evolution of Computer Technology". Milestones in Analog and Digital Computing. Springer. p. 1212. ISBN 978-3030409739.
^ Jager, Gerhard; Rogers, James (19 July 2012). "Formal language theory: refining the Chomsky hierarchy". Philosophical Transactions of the Royal Society B. 367 (1598): 1956–1970. doi:10.1098/rstb.2012.0077. PMC 3367686. PMID 22688632.
^ "John Warner Backus". February 2016. Retrieved 30 April 2021.
^ Hopcroft & Ullman (1979), 11장: 언어군의 폐쇄성

원천

인용작품

Hopcroft, John E.; Ullman, Jeffrey D. (1979). Introduction to Automata Theory, Languages, and Computation. Reading, Massachusetts: Addison-Wesley Publishing. ISBN 81-7808-347-7.

일반참고문헌

A. G. 해밀턴, 수학자들을 위한 논리학, 캠브리지 대학 출판부, 1978, ISBN 0-521-21838-1
Seymour Ginsburg, 공식언어의 대수적 및 오토마타 이론적 특성, North-Holland, 1975, ISBN 0-7204-2506-9
마이클 A. 해리슨, 공식언어이론개론, 애디슨-웨슬리, 1978
Rautenberg, Wolfgang (2010). A Concise Introduction to Mathematical Logic (3rd ed.). New York: Springer Science+Business Media. doi:10.1007/978-1-4419-1221-3. ISBN 978-1-4419-1220-6.
Grzegorz Rozenberg, Arto Salomaa, 공식 언어 안내서: I-III권, 스프링어, 1997, ISBN 3-540-61486-9
패트릭 서프스, 논리학 개론, D.Van Nostrand, 1957, ISBN 0-442-08072-7.

외부 링크

"Formal language", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
메릴랜드 대학교, 공식언어의 정의
제임스 파워, "형식 언어 이론과 파싱에 관한 노트" 2007년 11월 21일 웨이백 머신에서 보관, 2002년 11월 29일.
"형식 언어 이론 안내서" 제1권-3권, G. 로젠버그와 A장의 일부 장들의 초안.Salomaaa(eds.), Springer Verlag, (1997):
- Alexandru Mateescu and Arto Salomaa, Vol. 1의 "서면", pp. v-vii, 그리고 "형식 언어: 서론과 개요", 1권 1장, pp.1-39
- 성위, "정규언어" 제2권 1권
- 장 미셸 오테베르, 장 베르스텔, 뤽 보아송, "맥락 없는 언어와 밀어 내림 오토마타", 제3권
- Christian Choffrut and Juhani Karhumäki, "단어의 조합론", 제6장 1권
- Tero Harju and Juhani Karhumäki, "형태론", 제7장 1권, pp. 439–510
- Jean-Eric Pin, "Syntactic semigroups", 제10장 1권, 679-746쪽
- M. 크로치모어와 C.한카트, "매칭 패턴을 위한 오토마타", 제9장 2권
- Dora Giammarresi, Antonio Restivo, "2차원 언어", 4장 3권, 215-267쪽

[11] 예를 들어, 1차 논리는 종종 ¬, ∀, ∧, and, 괄호와 같은 기호 외에도 변수 역할을 하는 무한히 많은 요소 x, x, x, …를 포함하는 알파벳을 사용하여 표현됩니다.

[1] 예를 들어,Reghizzi, Stefano Crespi (2009). Formal Languages and Compilation. Texts in Computer Science. Springer. p. 8. Bibcode:2009flc..book.....C. ISBN 9781848820500. An alphabet is a finite set

[2] "In the prehistory of formal language theory: Gauss Languages". January 1992. Retrieved 30 April 2021.

[3] "Gottlob Frege". 5 December 2019. Retrieved 30 April 2021.

[Herken1279-4] Martin Davis (1995). "Influences of Mathematical Logic on Computer Science". In Rolf Herken (ed.). The universal Turing machine: a half-century survey. Springer. p. 290. ISBN 978-3-211-82637-9.

[5] "Thue's 1914 paper: a translation" (PDF). 28 August 2013. Archived (PDF) from the original on 30 April 2021. Retrieved 30 April 2021.

[6] "Emil Leon Post". September 2001. Retrieved 30 April 2021.

[7] 토레스 케베도, 레오나르도Sobrun Sistema de notaciones y symbolos destinados a facilityitar la descripción de las máquinas, (pdf), pp. 25-30, Revista de Obras Publicas, 1907년 1월 17일.

[Bruderer-8] Bruderer, Herbert (2021). "The Global Evolution of Computer Technology". Milestones in Analog and Digital Computing. Springer. p. 1212. ISBN 978-3030409739.

[9] Jager, Gerhard; Rogers, James (19 July 2012). "Formal language theory: refining the Chomsky hierarchy". Philosophical Transactions of the Royal Society B. 367 (1598): 1956–1970. doi:10.1098/rstb.2012.0077. PMC 3367686. PMID 22688632.

[10] "John Warner Backus". February 2016. Retrieved 30 April 2021.

[12] Hopcroft & Ullman (1979), 11장: 언어군의 폐쇄성

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[note 1]

[11]

Search

격식어

네임스페이스

더

목차

역사