복잡도 클래스

계산 복잡도 이론에서, 복잡도 클래스는 관련된 자원 기반 복잡도의 계산 문제 집합이다.가장 일반적으로 분석되는 두 가지 자원은 시간과 메모리입니다.

일반적으로 복잡도 클래스는 계산 문제의 유형, 계산 모델 및 시간 또는 메모리와 같은 제한된 자원의 관점에서 정의됩니다.특히, 대부분의 복잡도 클래스는 튜링 기계로 해결할 수 있는 결정 문제로 구성되며, 시간 또는 공간(기억) 요구 조건에 따라 구별됩니다.예를 들어, 클래스 P는 결정론적 튜링 기계에 의해 다항식 시간에 풀 수 있는 결정 문제의 집합이다.그러나 다른 유형의 문제(예: 문제 및 기능 문제 계산)와 다른 계산 모델(예: 확률론적 튜링 기계, 대화형 증명 시스템, 부울 회로 및 양자 컴퓨터)의 관점에서 정의된 많은 복잡도 클래스가 있다.

복잡도 클래스 간의 관계에 대한 연구는 이론 컴퓨터 과학의 주요 연구 분야입니다.복잡도 클래스에는 일반적인 계층이 존재하는 경우가 많습니다.예를 들어, 다수의 기본적인 시공간 복잡도 클래스는 서로 NL, P, NP, PSPACE, EXPTIME, EXPACE(여기서 「」는 서브셋 관계를 나타냅니다).그러나, 많은 관계가 아직 알려져 있지 않다. 예를 들어, 컴퓨터 공학에서 가장 유명한 미해결 문제 중 하나는 P가 NP와 같은지에 관한 것이다.클래스 간의 관계는 종종 계산의 근본적인 본질에 대한 질문에 답합니다.예를 들어, P 대 NP 문제는 비결정론이 컴퓨터에 계산 능력을 추가하는지 여부, 그리고 정확성을 빠르게 확인할 수 있는 해결책을 가지고 있는 문제도 빠르게 해결할 수 있는지에 대한 질문과 직접적으로 관련이 있습니다.

배경

복잡도 클래스는 관련된 계산 문제의 집합입니다.시간이나 메모리와 같은 특정 계산 자원에 관해 그 안에 포함된 문제를 해결하는 계산 난이도의 관점에서 정의됩니다.좀 더 형식적으로, 복잡도 클래스의 정의는 세 가지로 구성됩니다: 계산 문제의 유형, 계산 모델, 그리고 제한된 계산 자원.특히, 대부분의 복잡도 클래스는 제한된 시간 또는 공간 자원을 가진 튜링 기계에 의해 해결될 수 있는 결정 문제로 구성됩니다.예를 들어, 복잡도 클래스 P는 결정론적 튜링 기계에 의해 다항식 시간에 해결될 수 있는 결정 문제의 집합으로 정의된다.

계산상의 문제

직관적으로 계산 문제는 알고리즘으로 해결할 수 있는 문제일 뿐입니다.예를 들어 "$자연수{\displaystyle }$ n$\displaystyle$ n$"$은 계산상의 문제입니다.계산 문제는 수학적으로 그 문제에 대한 일련의 해답으로 표현된다.primality의 예에서 $({$ {PRIME$\})$는 소수인 모든 자연수의 집합으로 나타납니다. PRIME $=$ {${\displaystyle nn\mathbb{}}$ ${\displaystyle \text{N은 프라임}}$} {$displaystyle {PRIME$}=\{$n\in \mathbb {N} ntext {PRIME}$} $\}$ $。$계산 이론에서는 다음과 ${\displaystyle \mathtt{\text{같습니다}}}$.예를 들어 primality 예제에서는 자연수를 이진수를 나타내는 비트의 문자열로 나타낼 수 있습니다.이 때문에 비트 문자열이 형식 언어(언어학에서 차용한 개념)를 나타내기 때문에 계산 문제는 종종 동의어로 언어라고 불립니다.예를 들어 PRIME$(\${PRIME$})$ ${\displaystyle \mathtt{\text{문제}}}$가 복잡도 클래스 NP에 있다고 하는 것은 ${\displaystyle \mathtt{\text{언어}}}$ PRIME(\textt {textt {PRIME}}}${\displaystyle }${\$displaystyle {PRIME}}$은(는) NP입니다$.$

의사결정 문제

이론 컴퓨터 공학에서 가장 일반적으로 분석되는 문제는 의사 결정 문제, 즉 예/아니오 질문으로 제기될 수 있는 문제입니다.예를 들어, 위의 primality 예는 "natural $number{\displaystyle }$ n$\style$ n$"$ prime로 나타낼 수 있기 때문에 결정 문제의 한 예입니다.계산 이론의 관점에서, 결정 문제는 올바른 알고리즘을 실행하는 컴퓨터가 "예"라고 대답하는 입력 문자열 집합으로 표현됩니다.프라이머리 예에서 PRIME은$$자연수를$나타내는$ 문자열 세트입니다.PRIME을 올바르게 테스트하는 알고리즘을 실행하는 컴퓨터에 입력하면 알고리즘이 "네, 이 숫자는 프라임입니다"라고 응답합니다.이 "yes-no" 형식은 대부분의 경우 "accept-reject"로 표시됩니다.즉, 알고리즘은 결정 문제에 대한 대답이 "yes"이면 입력 문자열을 "accept"하고 "no"이면 "reject"합니다.

일부 문제는 의사결정 문제로 쉽게 표현될 수 없지만, 그럼에도 불구하고 광범위한 계산 ^[1]문제를 포함한다.특정 복잡도 클래스가 정의되는 다른 유형의 문제에는 함수 문제(예: FP), 계수 문제(예: #P), 최적화 문제 및 약속 문제가 포함된다(섹션 "기타 유형의 문제" 참조).

계산 모델

"컴퓨터"의 개념을 구체화하기 위해, 이론적인 컴퓨터 과학 문제들은 계산 모델의 맥락에서 분석됩니다.계산 모델은 "시간"과 "기억"과 같은 계산 자원의 정확한 개념을 만듭니다.계산 복잡도 이론에서 복잡도 클래스는 물리적 컴퓨터가 어떻게 구성되어 있는지에 따라 달라지는 자원 요건이 아니라 문제의 본질적인 자원 요건을 다룬다.예를 들어, 실제 환경에서는 컴퓨터마다 동일한 문제를 해결하기 위해 서로 다른 양의 시간과 메모리가 필요할 수 있습니다. 왜냐하면 컴퓨터는 설계되어 있기 때문입니다.컴퓨터의 추상적인 수학적 표현을 제공함으로써 계산 모델은 기본적인 원리를 이해하는 데 방해가 되는 현실 세계의 불필요한 복잡성(프로세서 속도의 차이 등)을 추상화합니다.

가장 일반적으로 사용되는 계산 모델은 튜링 기계이다.다른 모델들이 존재하고 많은 복잡도 클래스가 그것들의 관점에서 정의되는 반면, 튜링 기계는 대부분의 기본적인 복잡도 클래스를 정의하는데 사용된다.튜링 기계에서는 (실제 하드웨어 속도에서 실행 시간을 분리하는 것을 불가능하게 만드는) 두 번째와 같은 표준 시간 단위와 바이트와 같은 메모의 표준 단위를 사용하는 대신, 튜링 기계가 문제를 해결하기 위해 취하는 기본적인 단계의 수 및 메모의 개념으로 시간의 개념이 추상화된다.ry는 기계 테이프에서 사용되는 셀 수로 추상화됩니다.이하에, 보다 상세한 것에 대해 설명합니다.

구체적인 계산 모델을 참조하지 않고 복잡도 클래스를 정의하기 위해 Blum 공리를 사용하는 것도 가능하지만, 이 접근법은 복잡도 이론에서 덜 자주 사용됩니다.

결정론적 튜링 기계

튜링 기계는 일반적인 계산 기계의 수학적 모델이다.그것은 복잡도 이론에서 가장 일반적으로 사용되는 모델인데, 그 이유는 그것이 다른 계산 모델만큼 강력하고 수학적으로 분석하기 쉽다고 믿기 때문입니다.중요한 것은, 만약 특정한 문제를 해결하는 알고리즘이 존재한다면, 같은 문제를 해결하는 튜링 기계도 존재한다고 믿는다는 것이다(이것은 처치-튜링 논문으로 알려져 있다). 이것은 모든 알고리즘이 튜링 기계로 표현될 수 있다는 것을 의미한다.

기계적으로 튜링 머신(TM)은 무한히 긴 테이프에 포함된 기호(일반적으로 실제 컴퓨터에 직관적인 연결을 제공하기 위해 비트 0과 1로 제한됨)를 조작합니다.TM은 테이프 헤드를 사용하여 한 번에 하나씩 읽고 쓸 수 있습니다.동작은 "상태 42에서는 심볼이 0이면 1을 쓰고, 보이는 심볼이 1이면 17로 바꾸고, 상태 17에서는 심볼이 0이면 1을 쓰고, 상태 6으로 바꾼다" 등의 유한한 기본 명령에 의해 결정된다.튜링 머신은 테이프에 입력 문자열만 입력하고 다른 부분은 모두 공백으로 만듭니다.TM은 지정된 승인 상태가 되면 입력을 받아들이고 거부 상태가 되면 입력을 거부합니다.결정론적 튜링 기계(DTM)는 튜링 기계의 가장 기본적인 유형이다.향후의 액션을 결정하기 위해서, 고정 룰 세트를 사용합니다(이 때문에, 「결정론」이라고 불립니다).

계산 문제는 튜링 기계의 관점에서 특정 튜링 기계가 받아들이는 입력 문자열의 집합으로 정의될 수 있다.예를 들어 위에서 PRIME$(유효성$ $)$는 PRIME$($유효성 테스트) 알고리즘을 실행하는 튜링 기계가 받아들이는 문자열 세트(자연수를 나타냄)입니다.튜링 머신은 언어(계산 가능성과 복잡성 이론에서 "문제"와 "언어"가 대부분 동의어라는 호출)를 인식한다고 하며, 언어에 없는 모든 입력을 추가로 거부하면 언어를 결정한다고 한다(특정 입력이 튜링 머신을 작동시킬 수 있음).따라서 디시더빌리티는 튜링 머신이 모든 입력에서 정지해야 한다는 인식 가능성보다 추가적인 제약을 가한다.)문제를 해결하는 튜링 기계는 일반적으로 언어를 결정하는 기계를 의미합니다.

튜링 기계는 "시간"과 "공간"에 대한 직관적인 개념을 가능하게 한다.특정 입력에 대한 TM의 시간 복잡도는 튜링 기계가 승인 또는 거부 상태에 도달하기 위해 취하는 기본 단계의 수입니다.공간 복잡도는 테이프 상의 셀 수를 사용하여 허용 또는 거부 상태에 도달하는 것입니다.

비결정적 튜링 기계

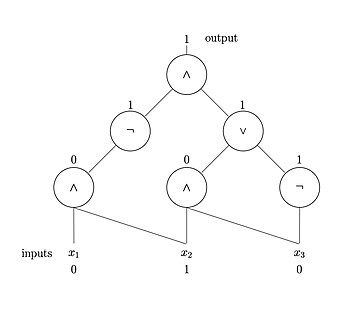
결정론적 튜링 머신(DTM)은 비결정론적 튜링 머신(NTM)의 변형이다.직관적으로 NTM은 주어진 상태에서 여러 가지 가능한 미래 행동을 탐색할 수 있는 추가 기능을 가진 일반적인 튜링 기계일 뿐이며, 이를 받아들이는 분기를 "선택"할 수 있다.즉, DTM은 계산의 한 가지 분기만 따라야 하지만 NTM은 계산 트리로 생각할 수 있으며, 각 단계에서 많은 가능한 계산 경로로 분기할 수 있습니다(이미지 참조).트리의 적어도1개의 브런치가 "accept" 조건으로 정지하면 NTM은 입력을 받아들입니다.이와 같이 NTM은 모든 계산 가능성을 병렬로 탐색하는 동시에 수용 ^[2]브랜치를 선택하는 것으로 생각할 수 있다.NTM은 물리적으로 실현 가능한 모델을 의미하는 것이 아니라 이론적으로 흥미로운 추상 머신으로 다수의 복잡한 클래스를 발생시킵니다(대부분 물리적으로 실현 가능한 동등한 정의를 가지고 있습니다).

NTM 의 시간 복잡도는,^[3] NTM 가 계산의 어느 브랜치에서도 사용하는 스텝의 최대수입니다.마찬가지로 NTM의 공간 복잡도는 NTM이 계산의 모든 분기에서 사용하는 셀의 최대 수입니다.

DTM은 비결정론의 힘을 이용하지 않는 NTM의 특수한 경우로 볼 수 있습니다.따라서 DTM에 의해 실행될 수 있는 모든 계산은 동등한 NTM에 의해서도 실행될 수 있습니다.또, DTM 를 사용해 NTM 를 시뮬레이트 할 수도 있습니다.따라서, 두 가지는 계산 가능성의 측면에서 동등합니다.단, NTM을 DTM으로 시뮬레이트하는 것은 많은 경우 더 많은 시간 및/또는 메모리 자원을 필요로 합니다.보시는 바와 같이 특정 종류의 계산 문제에서 이 속도가 얼마나 중요한지는 계산 복잡도 이론에서 중요한 질문입니다.

자원 한계

복잡도 클래스는 리소스 요구 사항을 기준으로 계산 문제를 그룹화합니다.이를 위해 계산 문제는 가장 효율적인 알고리즘이 이를 해결하기 위해 사용하는 자원의 최대 양에 따라 구분됩니다.특히 복잡도 클래스는 입력 크기가 커짐에 따라 특정 계산 문제를 해결하기 위해 필요한 자원의 증가율과 관련이 있습니다.예를 들어, 복잡도 클래스 P의 문제 해결에 걸리는 시간은 입력 사이즈가 커짐에 따라 다항식 속도로 증가하며, 지수 복잡도 클래스 EXPTIME의 문제(또는 보다 정확하게는 P ${\displaystyle \subseteq }$ ${\displaystyle \mathsf{E}}$ X ${\displaystyle \mathsf{P}}$ T ${\displaystyle \mathsf{T}}$ DISPLAY$$이기 $때문$에 P ${\displaystyle \mathsf{이외}}$의 EXPTIME의 문제)에 비해 $상대적$으로 느리다.$style {mathsf$ {P$}}\subseteq {mathsf {EXPTIME}}}.$

복잡도 클래스의 연구는 주로 계산 문제를 해결하는 데 필요한 고유한 복잡성을 이해하는 것을 목적으로 합니다.따라서 복잡도 이론가들은 일반적으로 문제가 속하는 최소 복잡도 클래스를 찾는 데 관심이 있으며, 따라서 계산 문제가 가장 효율적인 알고리즘을 사용하여 어떤 클래스에 속하는지 식별하는 데 관심이 있습니다.예를 들어, 지수 시간에 특정 문제를 해결하는 알고리즘이 있을 수 있지만, 이 문제를 해결하기 위한 가장 효율적인 알고리즘이 다항 시간에 실행된다면, 그 문제의 고유한 시간 복잡성은 다항식으로 더 잘 설명됩니다.

시간 범위

튜링 기계 모델에 대한 알고리즘의 시간 복잡도는 튜링 기계가 주어진 입력 크기에서 알고리즘을 실행하기 위해 걸리는 단계의 수이다.공식적으로 Turing $기계{\displaystyle }$M으로$구현$된 알고리즘의 시간 복잡도는 ${\displaystyle t_{}}$M : ${\displaystyle N\mathbb{}}$ ${\displaystyle \to }$ {{$M}$ : \$mathbb {N}$ \$to$ \$mathbb {N$으로 정의되며, $여기$서 ${\displaystyle t_{}}$M (${\displaystyle n}$) \$displaystyle$ $t_{M}(n)$은$$M의 $최대{\displaystyle }$ 단계 수이다.ut of $length{\displaystyle }$n(\$displaystyle$ n$)$입니다.

계산 복잡도 이론에서, 이론 컴퓨터 과학자들은 특정 런타임 값에 대한 관심이 적고, 시간 복잡도 함수가 속하는 일반적인 함수 클래스에 더 관심을 기울인다.예를 들어, 시간 복잡도 함수는 다항식입니까?로그 함수?지수함수?아니면 다른 종류의 기능인가요?

공간 경계

튜링 기계 모델에 관한 알고리즘의 공간 복잡도는 주어진 입력 크기에서 알고리즘을 실행하기 위해 필요한 튜링 기계의 테이프 상의 셀 수입니다.공식적으로 튜링 기계$M$으로$$구현된$$ $알고리즘$의 공간 복잡도는 ${\displaystyle 함수\mathbb{}}$ s ${\displaystyle M_{}}$: N ${\displaystyle \to }$ \$displaystyle s_{M:\mathbb {N}$ \$to$ \$mathbb {N$으로 정의되며${\displaystyle {}_{}}$ ${\displaystyle {여기}_{}}$서 M ($)\$$displaystyle$ $s_{M}(n)$은$$M의 $최대{\displaystyle }$ 셀 수이다.길이 $n$의$$t{$displaystyle$ n$\}.$

기본 복잡도 클래스

기본 정의

복잡도 클래스는 DTIME 및 NTIME(시간 복잡도) 및 DSPACE 및 NSPACE(공간 복잡도)라는 세분화된 복잡도 클래스 세트를 사용하여 정의되는 경우가 많습니다.빅 O 표기법을 사용하면 다음과 같이 정의됩니다.

• 시간 복잡도 $클래스{\displaystyle \mathsf{}}$ ${\displaystyle \mathsf{D}}$ T ${\displaystyle \mathsf{I}}$ ${\displaystyle \mathsf{M}}$ ${\displaystyle \mathsf{E}}$( ${\displaystyle t}$(${\displaystyle n}$ $){$ $displaystyle {DTIME}}(t(n$)})}는$$ O${\displaystyle }$(${\displaystyle t}$ ($)\display style$ O$(t(n)}$ 시간$$ 결정론적 튜링 $머신$에 의해 결정되는 모든 문제의 집합입니다.
• 시간 복잡도 $클래스{\displaystyle \mathsf{}}$ ${\displaystyle \mathsf{N}}$ T ${\displaystyle \mathsf{I}}$ M ${\displaystyle \mathsf{E}}$( ${\displaystyle t}$(${\displaystyle n}$) \ $displaystyle${ $NTIME}$ （$t$ ($n$ ) ） 。O$$ ${\displaystyle (}$ ${\displaystyle t}$(${\displaystyle n}$ $)\$ $display style$O ($t$ ($n$ )$시간$ 비결정론적 튜링 머신에 의해 결정되는 모든 문제의 집합입니다.
• 공간 복잡도 $클래스{\displaystyle \mathsf{}}$ ${\displaystyle \mathsf{D}}$ ${\displaystyle \mathsf{S}}$ ${\displaystyle \mathsf{P}}$ A ${\displaystyle \mathsf{C}}$ ${\displaystyle \mathsf{E}}$( ${\displaystyle s}$(${\displaystyle n}$ $){$ $displaystyle {DSPACE}}(s(n)})}$는 O${\displaystyle }$( ${\displaystyle s}$($){displaystyle$ O$(s(n)}}{$displaystyle O(s(n)}}}{displaystyle O(n)}}}}}{$공간$ 결정론적 튜링 머신에 의해 결정되는 모든 문제의 집합입니다.
• 공간 복잡도 $클래스{\displaystyle \mathsf{}}$ N ${\displaystyle \mathsf{S}}$ P ${\displaystyle \mathsf{A}}$ ${\displaystyle \mathsf{C}}$ E${\displaystyle }$( ${\displaystyle s}$(${\displaystyle n}$ $){$ $displaystyle {NSPACE}}(s(n$)})}는$$ ${\displaystyle O}$( ${\displaystyle s}$( n$){displaystyle$ O$(s($n)}{displaystyle O(s(n)})}공간$$ 비결정론적 튜링 머신에 $의해{\displaystyle }$ 결정되는 모든 문제의 집합입니다.

시간 복잡도 클래스

P와 NP

P는 결정론적 튜링 기계가 다항식 시간에 풀 수 있는 문제의 클래스이고, NP는 비결정론적 튜링 기계가 다항식 시간에 풀 수 있는 문제의 클래스입니다.좀 더 형식적으로 말하면

${\displaystyle {p}=\bigcup _{k\in\mathbb {N}}{\mathsf {DTIME}}(n^{k})$

${\displaystyle {NP}=\bigcup_{k\in\mathbb {N}}{\mathsf {NTIME}}(n^{k})$

P는 종종 결정론적 컴퓨터에 의해 "빠르게" 또는 "효율적으로" 해결할 수 있는 문제의 종류라고 불리는데, P의 문제 해결의 시간 복잡도는 입력 크기에 따라 상대적으로 느리게 증가하기 때문이다.

클래스 NP의 중요한 특징은 다항식 시간에 결정론적 튜링 기계에 의해 검증 가능한 해답을 갖는 문제의 클래스로 동등하게 정의될 수 있다는 것이다.즉, 문자열 ${displaystyle$ w$}$와 다항식 크기의 증명서 $문자열{\displaystyle }$ c${displaystyle$ c$\}$를 입력으로 사용하고 w${displaystyle$ w$}$가 언어 내에 $있으면{\displaystyle }$ w${displaystyle$ w$}$를 받아들이는 검증자라 불리는 결정론적 다항식 시간 튜링 머신이 존재하는 경우 언어는 NP에 있습니다.$s{\displaystyle }$ w$\displaystyle$w가$$$$ 언어에 없는 $경우{\displaystyle }$ w\$displaystyle$w.직관적으로 증명서는 입력 $\displaystyle$w가$$ 언어임을 증명하는 역할을 합니다.형식:^[4]

NP는 다항식 시간 결정론적 튜링 $머신{\displaystyle }$M({$displaystyle$M})과$$ $p$({$displaystyle$ p$})$가 존재하는$$L({$displaystyle$$L{\displaystyle }$}) 언어 클래스이며, 모든 $0,$1$\}^*\})$에 대해 w$({display style$ w$\in\$in\in\{$0,$\}^*})가$$L({*})에 있는 경우)와 w({$display$ style w$)$가 L$({\display$ style w)에 $있습니다{\displaystyle }$.${\displaystyle \mathrm{nly}}$ ( ${\displaystyle w}$$$) { $displaystyle c$\$in$ \ {$0$ , ${\displaystyle 1^{}}$ \$}^{$p ($w$ )${\displaystyle }$}${\displaystyle }$${\displaystyle {such}^{}}$ ${\displaystyle M}$ (${\displaystyle }$w${\displaystyle }$,$$c ) { $displaystyle M$( w$$, c ) } 이$$ $허용$된다.

비결정론적 정의와 검증자 정의 사이의 이러한 동등성은 비결정론과 솔루션 검증 가능성 사이의 근본적인 연관성을 강조한다.또, 언어가 NP 로 되어 있는 것을 증명하는 편리한 방법도 제공합니다.즉, 적절한 증명서를 간단하게 특정해, 다항식 시간에 검증할 수 있는 것을 나타냅니다.

P와 NP의 문제

효율적으로 해결할 수 있는 문제의 종류와 단순히 효율적으로 확인할 수 있는 문제의 종류 사이에는 분명한 차이가 있는 것처럼 보이지만, P와 NP는 사실 컴퓨터 과학에서 가장 유명한 미해결 문제 중 하나인 P와 NP의 중심에 있습니다.P ${\$ \$displaystyle \subseteq$NP$$ (직관적으로 결정론적 튜링 기계는 비결정론을 이용하지 않는 비결정론적 튜링 기계의 하위 클래스일 뿐이며, 검증자 정의에서 P는 다항식 시간 검증자가 빈 문자열만 증명으로 받으면 되는 문제의 클래스이다.ificate)는 NP가 P보다 큰지 여부를 알 수 없습니다.P=NP이면, 비결정론은 문제에 대한 해결책을 신속하게 찾을 수 있는 능력과 관련하여 결정론에 대한 추가 계산 능력을 제공하지 않는다. 즉, 가능한 모든 계산 분기를 탐색할 수 있는 것은 단 하나의 분기만 탐색할 수 있는 다항식 속도를 제공한다.또한 문제 인스턴스에 대한 증명이 존재하며 그 증명의 정확성을 신속하게 확인할 수 있는 경우(즉, 문제가 NP에 있는 경우), 그 증빙을 신속하게 구축할 수 있는 알고리즘도 존재합니다(즉, 문제가 P에 ^[5]있는 경우).그러나 대다수의 컴퓨터 과학자는 P ${\$ { $displaystyle$\ $neq }$ ^[6]NP$$ 및 오늘날 사용되는 대부분의 암호화 스킴은 P ${\$ \ $displaystyle$\$neq$} ^[7]NP라는 가정에 의존한다고 믿고 있습니다.

엑스타임과 넥스타임

EXPTIME은 결정론적 튜링 기계가 지수 시간에 해결할 수 있는 결정 문제의 클래스이고 NEXPTIME은 비결정론적 튜링 기계가 지수 시간에 해결할 수 있는 결정 문제의 클래스입니다.좀 더 형식적으로 말하면

${\displaystyle {EXPTIME}= 빅컵 _{k\in\mathbb {N}}{\mathsf {DTIME}}(2^{n^{k}})$

${\displaystyle {NEXPTIME}=\bigcup _{k\in \mathbb {N}}{\mathsf {NTIME}}(2^{n^{k}})$

EXPTIME은 P의 엄밀한 슈퍼셋이며 NEXPTIME은 NP의 엄밀한 슈퍼셋입니다.또한 EXPTIME $⊆$ \ $displaystyle$\$displayeq }$ NEXPTIME$$ 이 적절한지는 알 수 없지만 P=NP일 경우 EXPTIME은 NEXPTIME과 같아야 한다.

공간 복잡도 클래스

L 및 NL

로그 시간 복잡도 클래스를 정의할 수 있지만, 하위 선형 시간으로는 튜링 기계가 입력 전체를 읽을 수 없기 때문에(로그n <\$displaystyle \log$n <$n$}^[8] 이므로) 이러한 클래스는 매우 좁습니다.그러나 로그 공간에서 풀 수 있는 의미 있는 문제들이 많이 있다.이러한 클래스의 정의는 기계가 전체 입력을 저장할 수 있도록 하기 위해 2테이프 튜링 기계를 필요로 한다(계산 가능성 측면에서 2테이프 튜링 기계는 싱글테이프 튜링 ^[9]기계와 동등하다는 것을 보여줄 수 있다).2테이프 튜링 머신 모델에서는, 1개의 테이프가 읽기 전용의 입력 테이프입니다.다른 하나는 작업 테이프인데, 읽기와 쓰기를 모두 허용하고 튜링 기계가 계산을 수행하는 테이프입니다.튜링 기계의 공간 복잡도는 작업 테이프에 사용되는 셀의 수로 측정됩니다.

L은 결정론적 튜링 기계에서 로그 공간에서 해결 가능한 문제의 클래스로 정의되고 NL은 비결정론적 튜링 기계에서 로그 공간에서 해결 가능한 문제의 클래스입니다.좀 ^[9]더 형식적으로 말하면

$({displaystyle {L}}={DSPACE}}(\log n)})$

$({displaystyle {NL}}={NSPACE}}(\log n)})$

$L{\displaystyle \mathsf{}n\mathsf{}}$ ${\displaystyle \mathsf{N}}$ L${\displaystyle p\mathsf{}}$ P$$\ $displaystyle$\$mathsf${$L$} \ $subseteq$\$mathsf${ NL } \ $subseteq$\ $mathsf${ $P$}$$。다만, 이러한 관계가 적절한지는 알 수 없습니다.

PSPACE 및 NPSPACE

복잡도 클래스 PSPACE 및 NPSPACE는 P 및 NP와 유사한 공간입니다.즉, PSPACE는 결정론적 튜링 기계에 의해 다항식 공간에서 풀 수 있는 문제의 클래스이고, NPSPACE는 비결정론적 튜링 기계에 의해 다항식 공간에서 풀 수 있는 문제의 클래스이다.좀 더 형식적으로 말하면

${\displaystyle {PSPACE}=\bigcup _{k\in\mathbb {N}}{\mathsf {DSPACE}}(n^{k})}$

${\displaystyle {NSPACE}=\bigcup _{k\in \mathbb {N}}{\mathsf {NSPACE}}(n^{k})}$

P=NP인지는 알려지지 않았지만, Savitch의 정리는 PSPACE=NPSPACE로 잘 알려져 있다.$또한$ P$$machine \ displaystyle $\subseteq }$ PSPACE는 튜링 머신의 테이프상의 셀에의 기입이 1단위 시간이 걸리는 것으로 정의되어 있기 때문에 다항식으로 동작하는 튜링 머신은 다항식 셀에만 기입할 수 있는 것으로 알려져 있습니다.P는 PSPACE보다 확실히 작을 것으로 생각되지만, 이것은 증명되지 않았다.

EXPACE 및 NEXPSPACE

복잡도 클래스 EXPSPACE와 NEXPSPACE는 EXPTIME과 NEXPTIME의 공간유사체이다. 즉, EXPSPACE는 결정론적 튜링 머신에 의해 지수공간에서 풀 수 있는 문제의 클래스이고 NEXPSPACE는 비결정론적 튜링 머신에 의해 지수공간에서 풀 수 있는 문제의 클래스이다.좀 더 형식적으로 말하면

$({displaystyle {EXPACE}=\bigcup _{k\in\mathbb {N}}{\mathsf {DSPACE}}}(2^{n^{k}})$

${\displaystyle {NEXPSPACE}=\bigcup _{k\in\mathbb {N}}{\mathsf {NSPACE}}(2^{n^{k}})$

Savitch의 정리는 EXPSPACE=SMSPACE라는 것을 보여주었다.이 클래스는 매우 광범위합니다.PSPACE, NP, P의 엄밀한 슈퍼셋으로 알려져 있으며 EXPTIME의 엄밀한 슈퍼셋으로 간주됩니다.

복잡도 클래스의 속성

클로즈

복잡도 클래스에는 다양한 마감 속성이 있습니다.예를 들어, 의사결정 클래스는 부정, 분리, 연결 또는 모든 부울 연산에서 닫힐 수 있습니다.또한 다양한 정량화 체계에 따라 폐쇄될 수 있다.예를 들어 P는 모든 부울 연산에서 닫히고 다항식 크기의 도메인에서 정량화됩니다.닫힘 속성은 클래스를 분리할 때 도움이 될 수 있습니다.두 개의 복잡도 클래스를 분리할 수 있는 경로 중 하나는 하나의 클래스가 소유하고 있는 닫힘 속성을 찾는 것이지만 다른 클래스가 아닌 다른 클래스가 소유하고 있는 닫힘 속성을 찾는 것입니다.

부정으로 닫히지 않은 각 클래스 X에는 X에 포함된 언어의 보완어로 구성된 보완 클래스 co-X가 있습니다($예$를 들어 co-X$L$ {$L}$ {L$}}\in}$ $X$ $}$ {{$displaystyle \}$ {Displaystyle \}}$$ co-NP). 예를 들어, 하나의 중요한 보완 클래스입니다.co-NP=NP인지 아닌지에 대한 해결된 문제.

폐쇄 속성은 많은 복잡도 클래스가 ^[10]현재 방식으로 정의되는 주요 이유 중 하나입니다.예를 들어 O$)$ {$displaystyle$ O$(n)}$시간$$(즉 선형 시간) $내$에 해결할 수 있는 문제와 O${\displaystyle ({\mathrm{n}}^{}}$ 1000$)$ {$displaystyle$ O$(n^{1000})$ 시간$$ $내$에 해결할 수 있는 문제를 예로 들 수 있습니다.이 두 가지 문제는 모두 P에 있지만 입력 크기가 커짐에 따라 두 번째의 실행 시간이 첫 번째의 실행 시간보다 상당히 빠르게 증가합니다.이러한 큰 불일치를 허용하는 모든 다항식보다는 O${\displaystyle }$( ${\displaystyle {n\mathrm{}}^{}}$ 3$$)${\displaystyle {}^{}}$\$style$O ( $n$^ {3} $)$와 $같은{\displaystyle }$ 더 작은 다항식 경계를 사용하여 "효율적으로 해결 가능한" 문제의 클래스를 정의하는 것이 더 나은지 질문할 수 있다.그러나, 모든 다항식의 집합은 덧셈, 곱셈 및 구성 하에서 닫히는 선형 함수를 포함하는 최소 클래스의 함수이다(예를 들어,${\displaystyle }O{\displaystyle }$ (${\displaystyle {n\mathrm{}}^{}}$3)${\displaystyle o{}^{}}$ ( ${\displaystyle {n\mathrm{}}^{}}$ 2) ${\displaystyle ={}^{}}$ ( ${\displaystyle {n\mathrm{}}^{}}$ 6$$) \ $displaystyle$O ( n$$^$$2 ) = O ( n 6 ) \ $circ$O ( n$$^ {$n$ 2$=$O ( 6 ) ^ { $6$$display style$$O(n^{3}})$^[10] 입니다.는"효율적인 알고리즘"의 구성을 보장하기 때문에 우리는 또 다른 효율적인 알고리즘은 여전히 효율적인 것으로 간주되는 효율적인 알고리즘을 작곡하고 원하다항식의 클래스입니다.[11](은 P의 정의 때문인지, 실질적으로 말하면, P에 실질적으로 잘 돼 사실에 있어서 유용한 거의 모든 문제를 가지고 있는 유용합니다.낮은 차수의 다항식 런타임 및 실질적으로 유용한 P 이외의 거의 모든 문제에는 지수 런타임(즉${\displaystyle ,}$ O (${\displaystyle {}^{}{c}^{}}$ n$$)\$displaystyle$ O$(c^{n})$ $런타임$이 작은 알려진 알고리즘이 없습니다. 즉, c$\displaystyle$ c$}$는 1에 가깝습니다.)^[12]

삭감

많은 복잡도 클래스는 감소 개념을 사용하여 정의됩니다.감소는 한 문제를 다른 문제로 변환하는 것입니다.그것은 적어도 다른 문제만큼 문제가 어렵다는 비공식적 개념을 포착한다.예를 들어$$Y의 $알고리즘$을 사용하여 X$($$displaystyle$$$Y$)$ $문제$를 해결할 수 $있다면{\displaystyle }$ X$(displaystyle$ X$)$는 Y$(displaystyle$ Y$)$보다 어렵지 않으며 X$(displaystyle$ X$)$는 Y$(displaystyle$ Y$)$로 감소한다고 합니다.쿡 감소, 카르프 감소 및 레빈 감소와 같은 감소와 다항식 시간 감소 또는 로그 공간 감소와 같은 감소의 복잡성에 대한 한계.

가장 일반적으로 사용되는 감소는 다항식 시간 감소이며, 이는 단순히 감소 과정이 대부분의 다항식 시간이 걸린다는 것을 의미합니다.예를 들어 정수를 제곱하는 문제를 두 정수를 곱하는 문제로 줄일 수 있습니다.즉, 두 정수를 곱하는 알고리즘을 사용하여 정수를 제곱할 수 있습니다.따라서 제곱은 곱셈으로 줄일 수 있기 때문에 제곱은 곱셈보다 어렵지 않다는 것을 알 수 있습니다.

경도

감소는 복잡도 클래스에서 문제가 어렵다는 개념에 동기를 부여합니다.$C$의 모든 문제를 X$($ 스타일 X)로 줄일 수 있다면 문제 X$(디스플레이$ $스타일$ X$)$는 문제 C에 대해 어렵다.따라서 C의 $문제$는 X$($디스플레이$$ $스타일$ X$)$보다 $어렵다{\displaystyle }$.X$(디스플레이 스타일$ X)의 알고리즘에 의해 C의 문제를 해결할 수 있기 때문이다.물론 어려운 문제의 개념은 사용되는 감소 유형에 따라 달라집니다.P보다 큰 복잡도 클래스의 경우 다항식 시간 축소가 일반적으로 사용됩니다.특히 NP에게 어려운 문제의 집합은 NP-하드 문제의 집합입니다.

완전성

$문제{\displaystyle }$ X$($디스플레이$$ 스타일 X)가 C에 있고 C에 어려운 경우 X$(디스플레이 스타일$ X$)$는 C에 대해 완료라고 $합니다{\displaystyle }$.즉, X$($디스플레이$$ 스타일 X)는 C에서 가장 어려운 문제임을 $의미$합니다(X$(디스플레이 스타일$ X$)$는 $마찬가지$로 어려운 문제가 많을 수 있으므로 C에서 가장 어려운 문제만큼 어렵다고 할 수 있습니다.따라서 NP-완전 문제의 클래스는 P에 없을 가능성이 가장 높은 NP에서 가장 어려운 문제를 포함합니다.문제 P = NP가 해결되지 않기 때문에, 알려진 NP-완전 문제 δ를₂ 다른 문제 δ로₁ 줄일 수 있다면, δ에₁ 대한 알려진 다항식 시간 해법이 없다는 것을 나타낼 것이다.이는 δ에₁ 대한 다항식 시간 해법이 δ에₂ 대한 다항식 시간 해법을 산출하기 때문이다.마찬가지로, 모든 NP 문제를 집합으로 줄일 수 있기 때문에 다항식 시간에 풀 수 있는 NP-완전 문제를 찾는 것은 P = NP라는 것을 의미합니다.

복잡도 클래스 간의 관계

사비치의 정리

Savitch의 정리는 PSPACE = NPSPACE 및 EXPSPACE = NEXPSPACE를 설정합니다.복잡성 이론의 한 가지 핵심 질문은 비결정론이 계산 모델에 중요한 힘을 더하는가 하는 것이다.이것은 가장 중요한 두 가지 시간 복잡도 클래스를 다루는 열린 P 대 NP 문제의 중심입니다.Savitch의 정리는 공간의 경우 비결정론은 유의하게 더 많은 힘을 더하지 않는다는 것을 보여준다. 여기서 "significant"는 다항식 자원과 초다항식 자원 요구사항 사이의 차이(또는 EXPSPACE의 경우, 지수와 초특급수 사이의 차이)를 의미한다.예를 들어, Savitch의 정리는 결정론적 튜링 기계를 위한 지수 공간을 필요로 하는 어떤 문제도 비결정론적 다항식 공간 튜링 기계에 의해 해결될 수 없다는 것을 증명한다.

계층 정리

DTIME의 정의에 따르면 ${\displaystyle \mathsf{DTIME}({{nk\mathrm{}}_{}}^{}}$1$)({displaystyle$ {$DTIME})(n^{k_{1$})은 ${\displaystyle \mathsf{DTIME}({{nk2\mathrm{}}_{}}^{}}$에 포함되어 $있습니다{\displaystyle \mathsf{}}$({$displaystyle {dTIME$$}($$n^{$${\displaystyle {}_{}}$${$1})$$${\displaystyle {1k}_{}}$인 $경우{\displaystyle {}_{}}$${\displaystyle {ystyle\mathrm{}}_{}}$ O$(n^{k_{1})\subseteq$ O$(n^{k_{2}})$ k$$ 1${\displaystyle {}_{}{}_{}}$ ${\displaystyle {k\mathrm{}}_{}}$ 2$(\$일 $경우{\displaystyle {}_{}}$ 이 정의는 이 포함이 엄격한지 여부를 나타내지 않습니다.시간 및 공간 요건의 경우, 포함이 엄격한 조건은 각각 시간 및 공간 계층 이론에 의해 주어진다.이들은 각각의 자원을 제약함으로써 정의된 클래스에 적절한 계층을 유도하기 때문에 계층 이론이라고 불립니다.계층 이론은 해결할 수 있는 문제의 수를 늘리기 위해 얼마나 더 많은 시간 또는 공간이 필요한지에 대한 정량적 진술을 가능하게 한다.

시간 계층 정리는 다음과 같이 기술한다.

${\displaystyle \mathsf{D}}$ ${\displaystyle \mathsf{T}}$ ${\displaystyle \mathsf{I}}$ ${\displaystyle \mathsf{M}}$E (${\displaystyle f}$ (${\displaystyle n}$ )${\displaystyle d\mathsf{}}$ ${\displaystyle \mathsf{D}}$ T ${\displaystyle \mathsf{I}}$ ${\displaystyle \mathsf{M}}$E (${\displaystyle f}$ )${\displaystyle {\mathrm{2로그}}^{}}$ 2 ${\displaystyle {2\mathrm{}}^{}}$ (${\displaystyle }$f (${\displaystyle n}$ $){$ $display$ style { dTIME }{\$big ( n )$ }\$subsetneq${ $mathsf {DTIME}{\$big }($cdot)$

공간 계층 정리는 다음과 같이 기술한다.

${\displaystyle \mathsf{D}}$ S ${\displaystyle \mathsf{P}}$A ${\displaystyle \mathsf{C}\mathsf{E}}$ (${\displaystyle f}$ (${\displaystyle n}$ )${\displaystyle d\mathsf{}}$ D ${\displaystyle \mathsf{S}}$ ${\displaystyle \mathsf{P}}$ A ${\displaystyle \mathsf{C}\mathsf{E}}$ (${\displaystyle f}$ )${\displaystyle \mathrm{log로그}}$( (${\displaystyle f}$ (${\displaystyle n}$) $){$ $display${ $mathsf$ { DSPACE } { \ $big$( } \ $subsetneq${ $f$( n$){$f ( n $)$ } \ $space }$

시간과 공간 계층 정리는 복잡도 클래스의 대부분의 분리 결과의 기초를 형성합니다.예를 들어, 시간 계층 정리는 P가 EXPTIME에 엄밀하게 포함되는 것을 확립하고, 공간 계층 정리는 L이 PSPACE에 엄밀하게 포함되는 것을 확립한다.

기타 계산 모델

결정론적 튜링 기계와 비결정론적 튜링 기계가 가장 일반적으로 사용되는 계산 모델인 반면, 많은 복잡도 클래스는 다른 계산 모델의 관점에서 정의된다.특히,

• BPP, PP, RP 및 ZPP를 포함한 다수의 클래스가 확률론적 튜링 기계를 사용하여 정의된다.
• IP, MA 및 AM 클래스를 포함한 많은 클래스가 대화형 증명 시스템을 사용하여 정의됩니다.
• P/poly 클래스 및 그 서브 클래스 NC 및 AC를 포함한 많은 클래스가 부울 회선을 사용하여 정의됩니다.
• BQP 및 QMA 클래스를 포함한 많은 클래스가 양자 튜링 기계를 사용하여 정의됩니다.

이하에, 보다 상세한 것에 대해 설명합니다.

랜덤화 계산

랜덤 동전을 던질 수 있는 튜링 기계의 변형인 확률론적 튜링 기계를 사용하여 많은 중요한 복잡도 클래스가 정의된다.이러한 클래스는 랜덤화 알고리즘의 복잡성을 더 잘 설명하는 데 도움이 됩니다.

확률론적 튜링 기계는 결정론적 튜링 기계와 유사하며, 단 하나의 전이 함수(연산의 각 단계에서 어떻게 진행해야 하는지에 대한 규칙 집합)를 따르는 것이 아니라 확률적으로 각 단계에서 여러 전이 함수 중에서 선택한다.확률론적 튜링 기계의 표준 정의는 두 가지 전이 함수를 지정하기 때문에 각 단계에서 전이 함수를 선택하는 것은 동전 던지기와 유사합니다.계산의 각 단계에서 도입된 무작위성은 오류의 가능성을 야기한다; 즉, 튜링 기계가 받아들이도록 의도된 문자열은 어떤 경우에는 거부될 수 있고 어떤 경우에는 튜링 기계가 거부되도록 의도된 문자열이 받아들여질 수 있다.결과적으로, 확률론적 튜링 기계에 기초한 복잡도 클래스는 허용되는 오류의 양에 대해 대부분 정의된다.형식적으로는 오류 확률 ${\(\displaystyle \epsilon$을 사용하여 정의됩니다. 확률론적 튜링 $머신{\displaystyle }$M(\$displaystyle$ M$)$은 다음과 같은 경우 오류 확률$${\(\$displaystyle \epsilon)$의 언어$$L(\$displaystyle$ L$)$을 인식한다고 합니다.

1. $L$의$문자열{\displaystyle }$$$w {\$displaystyle$$$L$}$는 Pr$$ ${\displaystyle [\text{M}}$이${\displaystyle }$w를 ${\displaystyle 받아들임]\ge }$ ${\displaystyle 1}$-$${\ 、 （ \ $displaystyle${$Pr$} ） [ $M${ \$text${ accepts $}w$] \ $geq 1-$\ $epsilon }$을 의미합니다.
2. $L에$ $문자열$w {\$displaystyle$$$L$}$는 Pr$$${\displaystyle }$[ ${\displaystyle M}$ ${\displaystyle rejects}$ w${\displaystyle ]\ge }$ 1${\displaystyle }$-$${\ 、 ${\displaystyle \mathrm{q}}$ 1 - ${\displaystyle q}$ \ $displaystyle${$Pr$} [ $M${ \$text${ rejects $}w$] \ $geq 1-$\ $epsilon }$을 의미합니다.

중요 복잡도 클래스

기본적인 랜덤화 시간 복잡도 클래스는 ZPP, RP, co-RP, BPP 및 PP입니다.

가장 엄격한 클래스는 ZPP(제로 오류 확률 다항식 시간)로, 오류 확률이 0인 확률론적 튜링 기계에 의해 다항식 시간 내에 해결 가능한 문제의 클래스이다.직관적으로, 이것은 어떠한 오류도 요구하지 않기 때문에 확률론적 문제의 가장 엄격한 클래스이다.

약간 느슨한 클래스는 RP(랜덤화 다항식 시간)입니다.이 클래스는 언어에 없는 문자열에 대해서는 오류를 유지하지만 언어 문자열에 대해서는 경계 오류를 허용합니다.$좀$ 더 형식적으로 표현하면$,$ $문자열$이 언어로 되어 있지 않으면$M은 항상$ 거부하고 문자열이 언어로 되어 $있으면{\displaystyle }$M은 $적어도$ 1/2 확률로 받아들인다$.$co-RP 클래스도 마찬가지로 정의되지만 롤이 플립되어 있습니다.에러는 언어 문자열에는 허용되지 않지만 언어 이외의 문자열에는 허용됩니다.종합하면, RP와 co-RP는 단측 오류를 가진 확률론적 튜링 기계에 의해 해결될 수 있는 모든 문제를 포함한다.

양면 오차를 허용하기 위해 오류 요건을 더 완화하면 (언어 문자열이 아닌) 1/3 미만의 확률론적 튜링 기계에 의해 다항식 시간 내에 해결 가능한 문제의 클래스인 BPP(경계 오차 확률론적 다항식 시간)가 생성된다.BPP는 확률론적 복잡성 클래스 중 가장 실질적으로 관련이 있습니다. BPP의 문제는 실제 컴퓨터에서 빠르게 실행될 수 있는 효율적인 무작위 알고리즘을 가지고 있습니다.BPP는 또한 P=BPP인지 아닌지에 대한 컴퓨터 과학에서 중요한 미해결 문제의 중심에 있다. 이것은 무작위성이 컴퓨터의 계산 능력을 증가시키지 않는다는 것을 의미한다. 즉, 확률론적 튜링 기계는 다항식 감속으로 결정론적 튜링 기계에 의해 시뮬레이션될 수 있다.

효율적으로 해결 가능한 확률론적 문제의 가장 광범위한 클래스는 PP(확률론적 다항식 시간)이며, 이는 확률론적 튜링 기계가 모든 문자열에 대해 1/2 미만의 오류 확률로 다항식 시간에 해결할 수 있는 언어 집합이다.

ZPP, RP 및 co-RP는 모두 BPP의 서브셋이며, 다시 PP의 서브셋입니다.그 이유는 직관적입니다.오류가 제로인 클래스와 일방적인 오류만 허용하는 클래스는 모두 양면 오류를 허용하는 클래스 내에 포함되며 PP는 단순히 BPP의 오류 확률을 완화합니다.ZPP는 ${\displaystyle \mathsf{\text{다음}}}$과 같은 방법으로 RP 및 co-RP와 관련지어집니다.ZPP는 ${\displaystyle \mathsf{\text{ZPP}}}$ $=$ RP ${\displaystyle \cap }$ ∩ 、 ${\displaystyle \mathsf{\text{co-RP}}}$ ${$ $style$\$display$ { {$FRP$}$f${ $co$ - RP$$}$$。즉, ZPP는 RP와 co-RP 양쪽에 존재하는 문제로 구성되어 있습니다.직관적으로 이것은 RP와 co-RP가 단측 에러만을 허용하고 있기 때문에 발생합니다.co-RP는 언어의 문자열에 대한 에러를 허용하지 않으며 RP는 언어의 문자열에 대한 에러를 허용하지 않습니다.따라서 RP와 co-RP 모두에 문제가 있는 경우 언어(즉, 오류 없음)와 언어(즉, ZPP의 정의) 모두에서 문자열에 오류가 없어야 합니다.

중요한 무작위 공간 복잡도 클래스에는 BPL, RL 및 RLP가 포함된다.

인터랙티브한 증명 시스템

많은 복잡도 클래스가 대화형 증명 시스템을 사용하여 정의됩니다.대화형 증명은 복잡도 클래스 NP의 증명 정의를 일반화하고 암호학, 근사 알고리즘 및 형식 검증에 대한 통찰력을 제공합니다.

인터랙티브 프루프 시스템은 두 $($$Prover{\displaystyle }$ P {\$displaystyle$$$P$}$ 및 $검증자$ V {\$displaystyle$V$\})$ 간의 메시지 교환으로 계산을 모델링하는 추상 기계입니다.당사자는 메시지를 교환함으로써 대화하며 검증자가 프로바이더로부터 받은 메시지에 따라 입력을 받아들이기로 결정하면 입력 문자열이 시스템에 의해 받아들여집니다.$Prover{\displaystyle }$P {\$displaystyle$ P$}$는 무제한의 계산 능력을 가지지만 검증자는 제한적인 계산 능력을 갖습니다(인터랙티브 증명 시스템의 표준 정의에서는 검증자는 다항식 시간 제한으로 정의됩니다).단, 프로버는 신뢰할 수 없습니다(이것은 문자열이 언어 내에 있는지 계산되지 않은 프로버가 해결하도록 한 후 신뢰할 수 있는 "YES" 또는 "NO"를 검증자에게 전송함으로써 모든 언어가 증명 시스템에 의해 문제적으로 인식되는 것을 방지합니다).따라서 검증자는 "asking"하여 프로버의 "해독"을 수행해야 합니다.연속적인 질문의 회수는,^[13] 문자열이 언어에 있다고 하는 높은 신뢰도를 가지는 경우에 한정해 받아들여집니다.

중요 복잡도 클래스

클래스 NP는 검증자가 결정론적 다항식 시간 튜링 기계로 제한되고 절차가 한 라운드로 제한되는 단순한 증명 시스템입니다(즉, 프로버는 증명서라고 하는 하나의 완전한 증명서만 검증자에게 보냅니다).다른 방법으로, 클래스 NP(문제 인스턴스가 "YES"일 때 결정론적 튜링 기계에 의해 다항식 시간 내에 검증 가능한 증거를 갖는 결정 문제의 집합)의 정의에 있어서, 증명은 언급되지 않은 프로버에 의해 구성되고 결정론적 튜링 기계가 검증자가 되는 증명 시스템이다.이러한 이유로 NP는 dIP(결정론적 대화형 증명)라고도 할 수 있지만, 거의 그렇게 지칭되지 않습니다.

NP는 결정론적(다양한 시간) 검증자를 사용하여 인터랙티브 증명 시스템의 모든 힘을 포착하는 것으로 밝혀졌는데, 이는 결정론적 검증자를 가진 증명 시스템에 대해 프로버와 검증자 사이에 한 번 이상의 메시지가 필요하지 않음을 보여줄 수 있기 때문이다.따라서 표준 복잡도 등급에 비해 더 큰 계산 능력을 제공하는 대화형 증명 시스템은 확률론적 검증자를 필요로 한다. 즉, 검증자의 질문은 확률론적 알고리즘을 사용하여 계산된다.무작위 연산에 관한 절에서 설명한 바와 같이 확률론적 알고리즘은 시스템에 오류를 발생시키므로 확률론적 증명 시스템에 기초한 복잡도 클래스는 오류 확률의 관점에서 $정의$된다. §$$\$displaystyle \epsilon$ $\}$

이 특성화에서 발생하는 가장 일반적인 복잡도 클래스는 클래스 IP(인터랙티브 다항식 시간)이며, 클래스 IP(인터랙티브 다항식 시간)는 대화형 증명 시스템$({\displaystyle P}$,${\displaystyle V}$ $)({$displaystyle $(P,V$에서 해결할 수 있는 모든 문제의 클래스입니다. $여기$서$$V {$displaystyle$ V$}$는 확률론적 다항식 시간이고, 증명 시스템은 두 가지 속성을 만족합니다.r $언어{\displaystyle }$ L${\displaystyle i\mathsf{}}$ ${\displaystyle \mathsf{I}}$P { $displaystyle$L \$in$ { $mathsf${ $IP$} }

1. (완전성)$L$의 $문자열$w{$displaystyle$$$L$}$는 Pr${\displaystyle [\text{V}}$가${\displaystyle P}$와 ${\displaystyle \text{대화}}$한 후 ${\displaystyle \text{w}}$를 ${\displaystyle 받아들임}$]${\displaystyle 2\frac{\mathrm{}}{}}$ 2$$ \ \$display$ \$Pr$ [ $V${ \$text$ { accepts$} p와 대화$한 후 $w${ \$text$ { }$}$ \ $geq$ \$tfrac${$2$}
2. (사운드성)$$L에 $없는{\displaystyle }$ $문자열{\displaystyle }$ w${$$displaystyle$ L$}$는 ${\displaystyle Pr[\text{V}}$가${\displaystyle P}$와 $대화$한 후 ${\displaystyle \text{w}}$를 $]$ 1 ${\displaystyle \frac{3}{}}$\ \ $display$ \$Pr$ [ $V${ \$text$ { accepts $}w${ }$P$] \$leq$ { $tfrac${$$1$$} { } {$}$

IP의 중요한 기능은 PSPACE와 동등하다는 것입니다.다시 말해, 다항식 시간 인터랙티브 증명 시스템에 의해 풀릴 수 있는 모든 문제는 다항식 공간 자원을 가진 결정론적 튜링 기계에 의해서도 풀릴 수 있고, 그 반대도 마찬가지이다.

IP용 프로토콜을 수정하면 또 다른 중요한 복잡도 클래스인 AM(Arthur-Merlin 프로토콜)이 생성됩니다.IP가 사용하는 대화형 증명 시스템의 정의에서, 검증자는 확률론적 계산에서 검증자가 사용한 동전을 볼 수 없었다. 검증자가 이러한 동전으로 생성한 메시지만 볼 수 있었다.이러한 이유로, 그 동전들은 개인 랜덤 동전이라고 불린다.검증자가 사용하는 동전이 공개 랜덤 동전이 되도록 인터랙티브 프루프 시스템을 제한할 수 있습니다. 즉, 인증자가 동전을 볼 수 있습니다.형식적으로 AM은 검증자가 프로버에 랜덤 문자열을 송신하고, 프로버가 메시지로 응답하고, 검증자가 프로버로부터의 메시지에 결정론적 다항식 시간 함수를 적용하여 받아들이거나 거부하는 인터랙티브 증명이 있는 언어의 클래스로 정의된다.AM은 AM[k]로 일반화할 수 있습니다.여기서 k는 교환되는 메시지의 수(따라서 일반화된 형식에서 위에서 정의한 표준AM은 AM[2]입니다).단, $모든{\displaystyle }$ ${\displaystyle \mathrm{k\mu 2}}(\backslash$$displaystyle$ k$\geq$2)에 대해 AM[k]=AM [ 2 ]${\displaystyle A\mathsf{}}$ ${\displaystyle \mathsf{M}}$[ ${\displaystyle k}$]${\displaystyle }$i [ ${\displaystyle \mathsf{I}}$P [$]{ style$ \ $mathsf${$AM }$ } [ k $]\ subseteq$ \ mathsf { $IP$} [ $k$도 마찬가지입니다.

인터랙티브 증명 시스템을 사용하여 정의된 다른 복잡도 클래스에는 MIP(멀티프로버 인터랙티브 다항식 시간)와 QIP(양자 인터랙티브 다항식 시간)가 있습니다.

부울 회로

튜링 기계의 다른 계산 모델은 현대 컴퓨터에 사용되는 디지털 회로의 단순화된 모델인 부울 회로입니다.이 모델은 이론상의 계산과 실제의 계산 사이의 직관적인 연결을 제공할 뿐만 아니라, 불균일한 계산(같은 문제 내의 다른 입력 크기가 다른 알고리즘을 사용하는 계산)을 위한 자연스러운 모델입니다.

형식적으로 $부울{\displaystyle }$ $회로$C(\$style$ C$)$는 에지가 와이어(비트 값 0 및 1을 포함)를 나타내고 입력 비트가 소스 정점(착신 에지가 없는 수직)으로 나타내며 모든 비소스 정점이 논리 게이트(일반적으로 AND, OR 및 NOT 게이트)를 나타내는 방향 비순환 그래프입니다.하나의 로직 게이트는 출력 게이트로 지정되며 계산의 끝을 나타냅니다.n개의$$ $입력$변수를 가진 $회로{\displaystyle }$ C$(\$$displaystyle$C$)$의 입력/출력 동작은 부울 $함수{\displaystyle {}_{}}$ ${\displaystyle f_{}:}$ {${\displaystyle 0}$ , ${\displaystyle 1{}^{}}$} ${\displaystyle n^{}}$ ${\displaystyle \to }$ {${\displaystyle 0}$ , ${\displaystyle 1}$ $}$ { { $displaystyle f_{C$ : \ {$0$ , 1 \ }^{ $n }$ \ $to$\ {$0$ , 1 \$$} )로 ${\displaystyle {나타납니다}_{}.}예$를 들어 x ${\displaystyle ,}$2${\displaystyle {}_{}}$.{$n$ 회로의 출력 $비트{\displaystyle }$b {$style$ b$}$는 수학적으로 b $=$ ${\displaystyle {}_{}{C}_{}}$ ( ${\displaystyle {x\mathrm{}}_{}}$1, ${\displaystyle {x\mathrm{}}_{}}$2,${\displaystyle .,}$ x${\displaystyle {}_{}{n}_{}}$ $){display$ b$=f_{C}(x_${1},$x_{2},$x_${n$로 $표시$됩니다$.$$회로{\displaystyle }$C(\$displaystyle$ C$)$는 부울 $함수{\displaystyle {}_{}}$ F$(\$를 계산합니다.

특정 회로에는 입력 꼭지점 수가 고정되어 있기 때문에 해당 크기의 입력에만 동작할 수 있습니다.그러나 언어(의사결정 문제의 형식적 표현)는 길이가 다른 문자열을 포함하고 있기 때문에 언어가 단일 회로에 의해 완전히 포착될 수 없다(이는 언어가 어떤 입력 크기에 작용 가능한 단일 튜링 기계에 의해 완전히 기술되는 튜링 기계 모델과 대조된다).따라서 언어는 회로패밀리에 의해 표현된다.회선 패밀리는${\displaystyle {}_{}}$의 ${\displaystyle {무한\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}{C\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ C${\displaystyle {}_{}}$1, ${\displaystyle {C\mathrm{}}_{}}$ 2,${\displaystyle }$.${\displaystyle }$. $)(C_{0}, C_${1$}, C_{2$}, $...$ )입니다$.$${\displaystyle {여기}_{}}$서 Cn$(\displaystyle$ $C_{n})$은$$n개의 $입력$ 변수를 $가진{\displaystyle }$ 회선입니다.${\displaystyle {회로}_{}}$ 패밀리는 모든 $문자열{\displaystyle }$ w$\displaystyle$ w$\$displaystyle w\$displaystyle$ w$\$displaystyle$$ L$\$displaystyle L\displaystyle L$\$displaystyle $C_{n}(w$인 $경우$에만 $언어{\displaystyle }$ L$\$$displaystyle$ L을$$$$ 결정합니다. $여기$서 n$\displaystyle$n은$w$의 $길이입니다.$n 즉, 크기 ${displaystyle$ n$}$의 $문자열{\displaystyle }$ w${displaystyle$ w$}$는 회선${\displaystyle }$패밀리가 나타내는 $(C$, $C_{1}, C_{2}...)$로, 입력된 정점 번호와 같은 $회선{\displaystyle {}_{}}$ ${\displaystyle {번호}_{}}$의 C n${$})$$와$$ 같습니다.w$\displaystyle$ w$\}$의 문자는 w$\displaystyle$w가 입력된 $경우{\displaystyle }$ 1로 평가됩니다.

튜링 기계를 사용하여 정의된 복잡도 클래스는 시간 복잡도의 관점에서 설명되는 반면, 회로 복잡도 클래스는 회로 크기(회로 내의 정점 수)의 관점에서 정의됩니다.회로 패밀리$0,$ ${\displaystyle {}_{}{}_{}{1\mathrm{}}_{}}$, C$$ .$.$)의 크기 복잡도는 f${\displaystyle :N\mathbb{}}$ ${\displaystyle \to }$ {\$displaystyle$$$f$:\mathbb {N}$ $\backslash$$to \mathbb {N}$ 입니다.$여기$서 f$style$는 f$:n(style$)입니다$.$익숙한 함수 클래스는 여기서 자연스럽게 따라옵니다. 예를 들어 다항식 크기의 회로 패밀리는 $함수{\displaystyle }$ f$\style$f가$$ 다항식인 것입니다.

중요 복잡도 클래스

복잡도 클래스 P/poly는 다항식 크기의 회로 패밀리에 의해 결정되는 일련의 언어입니다.회로 복잡성과 시간 복잡성 사이에는 자연스러운 관계가 있는 것으로 나타났습니다.직관적으로 시간 복잡도가 작은 언어(즉, 튜링 기계에서 비교적 적은 수의 순차 연산을 필요로 함)는 또한 작은 회로 복잡도를 가진다(즉, 상대적으로 적은 수의 부울 연산을 필요로 함).형식적으로, 그것는 것은 만약 언어 DT에 있어서 ME(t(n)){\displaystyle{\mathsf{DTIME}}(t(n))}, t{\displaystyle지}은 기능 t:N→ N,\to \mathbb{N}}{\displaystyle t:\mathbb{N}.[14]그것은 dir를 따를 때면 그것은 회로 복잡도 O(t2(n)){\displaystyle O(t^{2}(n))}가 있는 것으로 나타날 수 있다.Ect.이 사실로부터 ${\displaystyle ly}$는 ${\$ P / ${\displaystyle \mathsf{\text{poly}}}${ $displaystyle$ {$mathsf${ $blue$}P$}}\subset {Textsf {P/poly$ 즉, 결정론적 튜링 기계로 다항 시간 내에 해결할 수 있는 문제는 다항식 크기의 회로 패밀리로도 해결할 수 $있습니다$.또한 P${\displaystyle p}$P / ${\displaystyle \mathsf{\text{poly}}}$（ \ $displaystyle$\ $textsf$ { P$}$ \$subsetneq$ \ textsf {$P$ / poly$$} $$）가 적절한 경우도 있습니다(예를 들어 P/poly에는 특정할 수 없는 문제가 있습니다).

P/poly에는 복잡도 클래스 간의 관계를 연구하는 데 매우 유용한 여러 특성이 있습니다.특히 P 대 NP와 관련된 문제를 조사하는 데 유용합니다.예를 들어 P/poly에 없는 언어가 NP에 있는 $경우{\displaystyle \mathsf{}}$ P${\displaystyle \mathsf{n}}$ N$$P \ $displaystyle$\$mathsf${$P$} \$neq$ \ $mathsf${ NP $}$^[15]. P/poly도 다항식 계층의 속성을 조사하는 데 도움이 됩니다.예를 들어 NP p P/poly일 경우 PH는 ${\displaystyle {2\mathrm{}}_{}^{}}$ 2$$ { $displaystyle$\ $Sigma$_ {$2}^{\mathsf {P$로 축소됩니다.P/poly와 기타 복잡도 클래스의 관계에 대한 자세한 설명은 "Importance of P/poly"에서 확인할 수 있습니다.P/poly는 또한 튜링 기계의 속성에 대한 일반적인 연구에서도 도움이 된다. 클래스는 다항식 경계 조언 함수를 가진 다항식 시간 튜링 기계에 의해 인식되는 언어의 클래스로 동등하게 정의될 수 있기 때문이다.

P/poly의 서브클래스는 NC와 AC입니다.이러한 클래스는 회로 크기뿐만 아니라 깊이에서도 정의됩니다.회로의 깊이는 입력 노드에서 출력 노드까지의 가장 긴 방향 경로 길이입니다.클래스 NC는 다항식 크기뿐만 아니라 다항식 깊이까지 제한되는 회로 패밀리로 해결할 수 있는 언어 집합입니다.클래스 AC는 NC와 유사하게 정의되지만 게이트에는 무제한 팬인이 허용된다(즉, AND 및 OR 게이트는 2비트 이상에 적용할 수 있다).NC는 효율적인 병렬 알고리즘을 가진 언어 클래스로 동등하게 정의될 수 있기 때문에 주목할 만한 클래스이다.

양자계산

이 섹션은 확장해야 합니다.추가해서 도와주시면 됩니다. (2017년 4월)

양자 정보 과학에서 중요한 BQP와 QMA 클래스는 양자 튜링 기계를 사용하여 정의됩니다.

기타 유형의 문제

컴퓨터 과학자들에 의해 연구된 대부분의 복잡도 클래스는 의사결정 문제의 집합이지만, 다른 유형의 문제에 대해서도 정의된 복잡도 클래스가 많이 있습니다.특히 계수 문제, 함수 문제, 약속 문제로 구성된 복잡도 클래스가 있습니다.이하에, 보다 상세한 것에 대해 설명합니다.

카운트 문제

카운트 문제는 솔루션이 존재하는지 여부(결정 문제와 마찬가지로)뿐만 아니라 솔루션이 ^[16]몇 개 존재하는지 묻습니다.${\displaystyle \mathtt{\text{예}}}$를 들어, 결정 문제$CYCLE$ {$style$$}은($는$)$ 특정 $G$에 단순한 사이클이 있는지 여부를 묻습니다(정답은 단순 예/아니오). 해당 카운트${\displaystyle \mathrm{}}$문제 #${\displaystyle \mathtt{\text{CYCLE}}}${$displaystyle \#{\textt$ {CYCLE$}}('$$하이프{\displaystyle }$ 사이클'로 발음)는 G의 단순 사이클 수를 묻습니다.$(*displaystyle$ G$)$^[17]가 가지고 있습니다.따라서 카운트 문제에 대한 출력은 단순한 예/아니오(또는 승인/거부, 0/1 또는 기타 동등한 방식)^[18]인 결정 문제에 대한 출력과는 달리 숫자입니다.

따라서 결정 문제는 수학적으로 공식 언어로 표현되는 반면 계수 문제는 수학적으로 함수로 표현됩니다. 계수 문제는 함수${\displaystyle }f{\displaystyle }$ :${\displaystyle }${ ${\displaystyle 0}$, ${\displaystyle 1{}^{}}$}${\displaystyle {}^{}}$∗${\displaystyle }$${\displaystyle {}^{}}$N {\${\displaystyle display\mathbb{}}$ $f:\{0,1\}^{*}\to$ \$mathbb${N$$$}\$to \mathbb {N}\$style${${\displaystyle 0{}^{}}$1$}\$ \display\}로 공식화됩니다$.$$0,1$${\displaystyle }f{\displaystyle }$( ${\displaystyle w}$ $),$ {$displaystyle f($w)}는$$ 솔루션의 수입니다.${\displaystyle \mathtt{\text{예}}}$를 들어$$#CYCLE {$displaystyle$$\#{\texttt {CYCLE}}$ 문제에서는$$ G $display{\displaystyle }${$0$ , ${\$ { $display$ G$\in$\ {$0$ , 1 \$$}^*} (비트 $$문자열로 표시되는 $그래프{\displaystyle )}$와 f ($G)$는$G스타일$의$$심플한 사이클 수입니다.

계수 문제는 통계적 추정, 통계물리학, 네트워크 설계, 경제 ^[19]등 여러 분야에서 발생합니다.

중요 복잡도 클래스

#^[20]P('샤프 P'로 발음)는 NP의 카운트 버전으로 생각할 수 있는 문제를 카운트하는 중요한 클래스입니다.NP와의 연결은 문제에 대한 해법의 수가 비결정론적 튜링 기계의 계산 트리에서 수용 분기의 수와 같다는 사실에서 발생한다.#P는 다음과 같이 정식으로 정의됩니다.

#P는 모든 $함수{\displaystyle }$f :${\displaystyle }${${\displaystyle }$0 , ${\displaystyle 1{}^{}}$} ${\displaystyle {\ast }^{}}$ ${\displaystyle {}^{}}$ {\$displaystyle$ f$:\{0$$,1$$\}^{*}\ to \mathbb {N}$의 집합이며, 모든 $w{\displaystyle \in }$ {${\displaystyle 0}$ , $}$ $디스플레이에 대해 다항식 시간$비결정론적 튜링 $머신{\displaystyle }$M {\$displaystyle$ M$}$이 존재한다$.$ping 브랜치는$$W$\backslash$^[20]$displaystyle$에 있는 M\$displaystyle$M의 계산 트리에 $있습니다{\displaystyle }$.

그리고 NP를 비결정론 및 검증자(즉 인터랙티브 증명 시스템)의 관점에서 정의할 수 있듯이, #P도 검증자의 관점에서 동등하게 정의할 수 있다.특정 문제 인스턴스에 대해 다항 시간 체크 가능한 증명서가 존재하는 경우, 즉 NP는 다항 시간 내에 정확성을 체크할 수 있는 입력에 대한 멤버십 증명서(증명서)가 존재하는지 여부를 묻습니다.클래스 #P는 이러한 증명서가 ^[20]몇 개 존재하는지 묻습니다.이 컨텍스트에서 #P는 다음과 같이 정의됩니다.

#P는 $다항식{\displaystyle }$${\displaystyle p\mathbb{}}$${\displaystyle :}$ ${\displaystyle \mathrm{N}}$ ${\displaystyle \to }$ N${\displaystyle {}^{}}$\$displaystyle$ p$:\mathbb {N}$ \$to$\$mathbb {N}$ 및 다항식$V-to$$$\$mathbb {N}$의 함수${\displaystyle \mathrm{집합}}$이다${\displaystyle .}$$yle$ w$\in \{0,1\}^{*}$,${\displaystyle }f{\displaystyle }$ (${\displaystyle w}$ ) ${\displaystyle =}$ { ${\displaystyle c\in }$ {${\displaystyle 0}$ , ${\displaystyle 1}$ ${\displaystyle {}^{}p}$ (${\displaystyle w^{}}$) :${\displaystyle }$V (${\displaystyle w}$ ,${\displaystyle c}$ ) ${\displaystyle =}$ ${\displaystyle 1}$ ${\displaystyle \}}$ { $display f$( w ) =$big$} {\ big \ { $0$, 1 \ $}$ c \ $in$\ { 0 , 1 \$}$p ( $w$) :$V(w,c)=1{\big \}}{\$Big$\}\}.$^[21] 즉${\displaystyle ,}$ ${\displaystyle f(}$w$){displaystyle f($w)}는 w$(\displaystyle$ w$)$의 모든 다항식 크기 증명서를 포함하는 세트의 크기입니다.

기능상의 문제

계수 문제는 함수 문제라고 불리는 광범위한 종류의 문제의 하위 집합입니다.함수 문제는 $함수{\displaystyle f}$의 값이 A ${\displaystyle \to }$ {$displaystyle$f:}인 문제의 유형입니다.$A\to$ B$}$가 계산됩니다.$형식적$으로 함수 $f$는 임의의 알파벳 ${\$ $문자열$에 대한 R$(\$$displaystyle\Sigma$로 정의됩니다.

${\displaystyle R\subseteq\Sigma ^{*}\times \Sigma ^{*}}$

알고리즘은 입력 $($${\displaystyle x}$, ${\displaystyle y}$ )${\displaystyle r}$R \ $display$ style $( x$ , y )를 만족시키는${\displaystyle }$$y{\displaystyle }$$\$ $displaystyle$ ($$x , y )가$존재$하도록$$각 입력 x(\ $displaystyle$$$x$)$에 대해$$$해결$합니다.이는 f$${\$displaystyle$ f$}$가 함수이며 알고리즘은${\displaystyle }$f (x$$) {$displaystyle$ f$(x)}$을(를) 모든 x${\displaystyle {\mathrm{}}^{}}$ ${\$ {\$displaystyle$ x$\in \Sigma$ $^\{*\}$에 대해 $해결$한다는 $것$을 나타내는 또 다른 방법입니다.

중요 복잡도 클래스

중요한 함수 복잡도 클래스는 효율적으로 해결 가능한 ^[21]함수의 클래스인 FP입니다.보다 구체적으로 FP는 결정론적 튜링 기계에 의해 다항식 시간에 해결될 ^[21]수 있는 함수 문제의 집합이다.FP는 P와 동등한 함수 문제로 생각할 수 있습니다.중요한 것은 FP가 카운트 문제와 P 대 NP 모두에 대한 통찰력을 제공한다는 것입니다.#P=FP일 경우, NP의 문제에 대한 인증서 수를 결정하는 함수는 효율적으로 해결할 수 있습니다.증명서 수 계산은 적어도 증명서가 존재하는지 여부를 판별하는 것만큼 어렵기 때문에 #P=FP일 경우 P=NP가 그 반대인지, 즉 P=NP가 ^[21]#P=FP를 의미하는지 여부를 알 수 없음)를 따라야 합니다.

FP가 P에 상당하는 함수 문제인 것처럼 FNP는 NP에 상당하는 함수 문제입니다.중요한 것은 FP=FNP인 경우 및 P=^[22]NP인 경우에만 FP=FNP이다.

약속 문제

약속 문제는 문제에 대한 입력이 가능한 모든 입력의 특정 부분 집합으로부터 보장("약속")되는 의사결정 문제의 일반화입니다.결정 $문제{\displaystyle }$ L ${\displaystyle \{}$ {${\displaystyle }$0 , ${\displaystyle 1{}^{}}$}${\$ { \ $displaystyle$L \ $subseteq \${ 0 , 1 \ $}^{$ *$$}} a $、$ L { \ $displaystyle$$$L$$}의$$ $알고리즘{\displaystyle }$$$M은 $모든$ w ${\displaystyle \{0}$ , ${\displaystyle 1}$ $}$ $a{\displaystyle }$ { \ $display style$ w $\ 0$ , 1 \ loose $\}$의 약속에 대해 올바르게 동작해야 합니다.y 입력이 {${\displaystyle 0}$ , ${\displaystyle 1{}^{\}}}$의${\displaystyle }$일부 서브셋으로 제한됩니다.{ $displaystyle$\ { 0 , 1 \$$}^{ *$$。

구체적으로는 약속 문제는 교차하지 않는 세트${\displaystyle }$쌍( of ACCEPT${\displaystyle {}_{}}$ ${\displaystyle {\text{π}}_{}}$REJECT$)$으로 정의됩니다.\ $displaystyle$( \ $Pi$ _ { \ $text$）$ACCEPT}},\Pi _{\text{$REJECT$\}\}\}\}\},$ $여기$서:^[23]

• $1$$$ACCEPT$}}\subseteq \{0$,1$\}^{*}$는 허용되는 모든 입력의 집합입니다.
• $1$$$REJECT$}\subseteq$\{$0,1\}^{*}$는 거부된 모든 입력의 $집합$입니다.

약속${\displaystyle }$문제에 대한 $알고리즘{\displaystyle }$M {\$displaystyle$ M$}$ 입력$$( ${\displaystyle {\text{π}}_{}}$ACCEPT , ${\displaystyle {\text{reject}}_{}}$REJECT $){$ $displaystyle$( \ $Pi$ _ { \ $text$} )$ACCEPT}},\Pi _{\text{$REJECT$}}$는 ${\displaystyle {\text{is}}_{}}$ ACCEPT ${\displaystyle {}_{}}$ ${\displaystyle {\text{REJECT}}_{}}${ $displaystyle$\ $Pi$ _ { \ $text$} 입니다.$ACCEPT}}\cup \Pi _{\text{$REJECT$\}\}.$ 이를 약속이라고 $합니다$.${\displaystyle {\mathrm{}}_{}}$ ACCEPT ${\displaystyle {}_{}}$ ${\$ ${\displaystyle {\text{REJECT}}_{}}$ \ $displaystyle$\$Pi$ _ { \ text$$}의 문자열$ACCEPT}}\cup \Pi _{\text{$REJECT$}}}$이(^[23]가) 약속을 충족한다고 합니다.정의상 ${\displaystyle {\text{π}}_{}}$ ACCEPT$$(\$displaystyle \Pi$) _${\text${\text$}$ACCEPT$}}$ 및$$ ${\displaystyle {\text{π}}_{}}$ REJECT$($ 스타일$)_{\text{$REJECT$}}$은(는) 분리되어야 합니다. 즉, ${\displaystyle {\text{π}}_{}}$ ACCEPT ${\displaystyle {}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {\text{π}}_{}}$ REJECT ${\displaystyle {}_{}}$ { \ $displaystyle$\ $Pi$ _ { \$$$text$ { }$ACCEPT}}\cap \Pi _{\text{$REJECT$}=\emptyset$ 입니다.

이 공식에서 의사결정 문제는 사소한 약속 ${\displaystyle {\text{π}}_{}}$ ACCEPT ${\displaystyle {}_{}}$ ${\displaystyle {\text{π}}_{}}$ REJECT${\displaystyle =}$ { ${\displaystyle 0{}^{}}$, 1 }${\$ \ $display$ \ Pi $_$ { \ text $}$의 약속 문제의 서브셋에 불과함을 알 수 있다.$ACCEPT}}\cup \Pi _{\text{$REJECT$}=\{0,1$ 결정상의 문제가 있는 경우 문제를 단순히 ${\displaystyle {\text{π}}_{}}$ ACCEPT$(\$$displaystyle \Pi$)로 정의하는 것이 $보다$ 간단합니다$.$ACCEPT$}}($${\displaystyle {\text{δ}}_{}}$ REJECT$\$ 사용)$_$${\text{$REJECT$}}$은$({\displaystyle }$는) 암묵적으로 {$0,$ 1${\displaystyle {}^{}}$}${\displaystyle {}^{}}$ / ${\$ ACCEPT ${\displaystyle$\{$0,$1\}^{*} / $\$Pi _${\text${}입니다.ACCEPT$}})$는 이 페이지 전체에서 L$(\displaystyle$ L$)$로 표시되며, 이는 ${\displaystyle {\text{δ}}_{}}$ ACCEPT$$(\$displaystyle$ \$Pi$)_${\text{\$text})임을 강조하기 위해 $사용$됩니다.ACCEPT$}=L}$은 정식 언어입니다.

약속 문제는 많은 계산 문제를 보다 자연스럽게 공식화합니다.예를 들어, 계산상의 문제는 "평면 그래프를 지정하면 ^[24]그 여부를 판단한다"와 같은 경우가 있습니다.이는 종종 모든 $문자열{\displaystyle }$ ${\displaystyle \{}$ { 0${\displaystyle }$, ${\displaystyle 1{}^{}}$} ${\$ { $display style$s \ $in$\ {$0$ , 1 \ $}^*}^*}$ 를$$ 평면 그래프로 변환하는 변환 스키마가 있다고 가정하고 있습니다.단, 이것을 입력이 평면 그래프로 약속되는 약속 문제로 정의하는 것이 보다 간단합니다.

복잡도 클래스와의 관계

약속 문제는 의사결정 문제의 표준 복잡도 클래스에 대한 대체 정의를 제공합니다.예를 들어 P는 약속 ^[25]문제로 정의할 수 있습니다.

P는 결정론적 다항 시간에 풀 수 있는 약속 문제의 클래스입니다.즉, 약속 문제$({\displaystyle }$ ${\displaystyle {}_{}}$ ACCEPT , ${\displaystyle {\text{reject}}_{}}$REJECT $){$ $displaystyle$( \ $Pi$ _ { \ $text$} )$ACCEPT}},\Pi _{\text{$REJECT$}}}$는 다음과 같은 다항식 시간 알고리즘 $({displaystyle$M$$})이 존재하는 경우 P에 있습니다.

• $모든{\displaystyle }$ x${\displaystyle {\text{δ}}_{}}$ ACCEPT${\displaystyle {}_{}M}$ (${\displaystyle x}$ ) ${\displaystyle =}$ ${\displaystyle 1}$\ $displaystyle$x \ $in$\ $Pi$ _ { \ \$$$text$ {$ACCEPT}}, M(x)=1}$
• ${\displaystyle \mathrm{ever}}$ x ${\displaystyle \in }$ ${\displaystyle {}_{}}$ ${\displaystyle {\text{REJECT}}_{}}$, M${\displaystyle }$( ${\displaystyle x}$ ) ${\displaystyle =}$ \ $displaystyle x$\ $in$ \ $Pi$ _ { \ $text$}$REJECT}}, M(x)=0}$

의사결정 문제의 클래스, 즉 정식 언어로 정의된 문제의 클래스는 약속 문제로 자연스럽게 변환됩니다.여기서 클래스 내 L$(\display style$ L$=\Pi$) $언어$는 $단순히{\displaystyle }$ L ${\displaystyle =}$ ${\displaystyle {\text{π}}_{}}$ ACCEPT$(\$ L=\$Pi$)입니다$.{\text{$ACCEPT$}}$ 및$$ ${\displaystyle {\text{π}}_{}}$ REJECT$($ 스타일$)_{\text{$REJECT$}}$는${\displaystyle \mathrm{암묵적}}$으로 { 0${\displaystyle }$, ${\displaystyle 1{}^{}}$}${\displaystyle {}^{}}$ / $π$ ACCEPT$${ $0$, 1 \ }^{ * } / \ $Pi$ _ { \ $text {$ \ text {$ACCEPT$

P와 같은 많은 기본 복잡도 클래스를 약속 문제로 공식화하는 것은 그 특성에 대한 추가적인 통찰력을 거의 제공하지 않습니다.그러나, 그것들을 약속의 문제로 공식화하는 것이 컴퓨터 과학자들에게 유용한 몇 가지 복잡도 클래스가 있습니다.예를 들어 약속 문제는 SZK(통계 제로 지식)^[26] 연구에 중요한 역할을 했다.

복잡도 클래스 간의 관계 요약

다음 표는 복잡도 이론에서 고려되는 몇 가지 종류의 문제를 보여줍니다.클래스 X가 Y의 엄밀한 서브셋인 경우, X는 Y의 아래쪽에 어두운 선이 연결되어 표시됩니다.X가 서브셋이지만 동일한 집합인지 여부를 알 수 없는 경우 선은 더 가볍고 도트가 있습니다.엄밀히 말하면, 결정가능성과 결정불가능성으로의 분류는 계산가능성 이론의 연구와 더 관련이 있지만, 복잡도 클래스를 원근법에 두는 데 유용하다.

		의사결정 문제
유형 0(재귀 열거형)				결정 불가
결정 가능
엑스페이스
넥스트 타임
제외 시간
PSPACE
타입 1(콘텍스트 의존)
		co-N	BQP		NP
			BPP
		P
	엔씨
타입 2(콘텍스트프리)
타입 3(통상)

「 」를 참조해 주세요.

• 복잡도 클래스 목록

레퍼런스

참고 문헌

• Aaronson, Scott (8 January 2017). "P=?NP". Electronic Colloquim on Computational Complexity. Weizmann Institute of Science. Archived from the original on June 17, 2020.
• Arora, Sanjeev; Barak, Boaz (2009). Computational Complexity: A Modern Approach. Cambridge University Press. Draft. Archived from the original on February 23, 2022. ISBN 978-0-521-42426-4.
• Arora, Sanjeev (Spring 2003). "Complexity classes having to do with counting". Computer Science 522: Computational Complexity Theory. Princeton University. Archived from the original on May 21, 2021.
• Barak, Boaz (Spring 2006). "Complexity of counting" (PDF). Computer Science 522: Computational Complexity. Princeton University. Archived from the original on April 3, 2021.
• Fortnow, Lance (1997). "Counting Complexity" (PDF). In Hemaspaandra, Lane A.; Selman, Alan L. (eds.). Complexity Theory Retrospective II. Springer. pp. 81–106. ISBN 9780387949734. Archived from the original (PDF) on June 18, 2022.
• Gasarch, William I. (2019). "Guest Column: The Third P =? NP Poll" (PDF). University of Maryland. Archived (PDF) from the original on November 2, 2021.
• Goldreich, Oded (2006). "On Promise Problems: A Survey" (PDF). In Goldreich, Oded; Rosenberg, Arnold L.; Selman, Alen L. (eds.). Theoretical Computer Science. Lecture Notes in Computer Science, vol 3895 (PDF). Lecture Notes in Computer Science. Vol. 3895. Springer. pp. 254–290. doi:10.1007/11685654_12. ISBN 978-3-540-32881-0. Archived (PDF) from the original on May 6, 2021.
• Rich, Elaine (2008). Automata, Computability and Complexity: Theory and Applications (PDF). Prentice Hall. ISBN 978-0132288064. Archived (PDF) from the original on January 21, 2022.
• Sipser, Michael (2006). Introduction to the Theory of Computation (PDF) (2nd ed.). USA: Thomson Course Technology. ISBN 0-534-95097-3. Archived from the original (PDF) on February 7, 2022.
• Watrous, John (April 11, 2006). "Lecture 22: Quantum computational complexity" (PDF). University of Waterloo. Archived (PDF) from the original on June 18, 2022.

추가 정보

• Wayback Machine에 보관된 2019-08-27 복잡성 동물원:복잡도 클래스의 방대한 리스트, 전문가의 참고 자료.
• Neil Immerman. "Computational Complexity Theory". Archived from the original on 2016-04-16. 복잡도 클래스의 계층과 클래스 간의 적합성을 보여주는 다이어그램을 포함합니다.
• 마이클 개리, 데이비드 S. 존슨: 컴퓨터와 난해성: NP-완전성 이론 가이드.뉴욕: W. H. Freeman & Co., 1979.NP-완전 문제에 대한 표준 참조 - 솔루션에 실무적으로 긴 시간이 필요한 문제의 중요한 범주입니다.