기준범위
Frame of reference| 시리즈의 일부 |
| 고전 역학 |
|---|
물리학과 천문학에서 기준 프레임(또는 기준 프레임)은 수학적으로 (숫자 좌표 값으로) 그리고 물리적으로 (기하학적)[1] 위치가 식별되는 일련의 기준점에 의해 지정되는 추상 좌표계이다.
n개의 치수의 경우 n + 1개의 기준점으로 기준 프레임을 완전히 정의할 수 있습니다.직사각형 데카르트 좌표를 사용하여 기준 프레임은 원점에 기준점을, 그리고 각 n개의 좌표축을 [citation needed]따라 하나의 단위 거리에 기준점을 사용하여 정의할 수 있습니다.
아인슈타인 상대성 이론에서 기준 프레임은 움직이는 관찰자와 관찰 중인 현상 사이의 관계를 규정하는 데 사용됩니다.이 맥락에서 용어는 종종 관측 기준 프레임 또는 관측 기준 프레임이 됩니다. 이는 관측자가 반드시 원점에 위치하지는 않지만 프레임에 정지해 있음을 의미합니다.상대론적 기준 프레임은 서로 상대적으로 이동하는 서로 다른 기준 프레임 간에 등가하지 않는 좌표 시간을 포함하거나 암시한다.따라서 상황은 모든 가능한 좌표 시간이 본질적으로 [citation needed]동일한 갈릴레이 상대성 이론과는 다릅니다.
정의.
'참조범위'의 다양한 의미를 구별할 필요가 있기 때문에 다양한 용어가 생겨났다.예를 들어, 데카르트 기준 프레임에서와 같이 좌표계 유형이 수식자로 부착되는 경우가 있습니다.회전 기준 프레임에서처럼 운동 상태가 강조되는 경우가 있습니다.때로는 갈릴레이 기준 프레임에서와 같이 관련된 것으로 간주되는 프레임으로 변환하는 방법이 강조됩니다.때때로 프레임은 거시적 및 미시적 [2]기준 프레임에서와 같이 관측치의 규모에 따라 구별된다.
이 기사에서 관측 기준 프레임이라는 용어는 관측 또는 관측 장치의 좌표 선택이나 특성보다는 운동 상태에 중점을 둘 때 사용된다.그런 의미에서 관찰 기준 프레임을 사용하면 이 프레임에 부착할 수 있는 좌표계 전체군에 대한 움직임의 영향을 연구할 수 있습니다.한편, 좌표계는 운동 상태가 주요 관심사가 아닌 다양한 목적을 위해 사용될 수 있다.예를 들어 좌표계를 채용하여 시스템의 대칭성을 이용할 수 있다.더 넓은 관점에서, 물리학에서 많은 문제의 공식은 공간과 시간과 간접적으로만 관련이 있는 일반화 좌표, 정규 모드 또는 고유 벡터를 사용합니다.아래의 논의를 위해 참조 프레임의 다양한 측면을 분리하는 것이 유용할 것 같습니다.따라서 우리는 다음과 같이 분리된 독립적인 개념으로 기준, 좌표계 및 관측 장비를 사용한다.
- 관찰 프레임(관성 프레임 또는 비관성 기준 프레임 등)은 운동 상태와 관련된 물리적 개념이다.
- 좌표계는 [3]관찰을 기술하는 데 사용되는 언어를 선택하는 수학적 개념이다.따라서 관찰 기준 프레임의 관찰자는 그 기준 프레임에서 만들어진 관찰을 기술하기 위해 좌표계(카르트, 극, 곡선, 일반화 등)를 사용할 수 있다.이 좌표계의 선택이 바뀌어도 관찰자의 운동 상태는 변하지 않으며, 따라서 관찰자의 관찰 기준 프레임에 변화가 수반되지 않는다.이 관점은 다른 곳에서도 찾아볼 수 있다.[4]즉, 일부 좌표계가 다른 관측치보다 더 나은 선택일 수 있다는 것에 이의를 제기하는 것은 아니다.
- 무엇을 그리고 어떤 관측 장치로 측정할지의 선택은 관찰자의 운동 상태 및 좌표계 선택과는 별개의 문제이다.
이동 관측 R 및 관련 유클리드 3공간 좌표계 [R, R r 등][5]에 적용할 수 있는 인용문입니다.
우리는 먼저 기준 프레임의 개념을 소개하는데, 그 자체는 관찰자의 생각과 관련이 있다: 기준 프레임은 어떤 의미에서는 "관찰자가 운반하는 비유클리드 공간"이다.좀 더 수학적인 정의를 내리겠습니다.참조 프레임은...관찰자의 강체 운동을 가진 유클리드 공간의 모든 점들의 집합.R로 된 프레임은 관찰자와 함께 움직인다고 합니다.원점 O의 좌표계 R을 설정하여 R을 기준으로 파티클의 공간 위치를 라벨링합니다({의강체 운동을 공유하는 대응하는 축 세트는 프레임의 강체 운동을 으로 실현하는 것으로 볼 수 있으며, 의 경우 각 순간마다 좌표가 R에서 로 바뀝니다f 시간, 이 프레임의 물리적 양을 나타내기 위해 도입된 고유 물체(표준 및 텐서)의 구성요소에 대한 동일한 좌표 변환.
그리고 Rmathfrak {R})과 [R, R, 등][6]의 을 분리하는 유틸리티에 관한 것입니다.
Brilouin이 지적한 바와 같이, 수학적 좌표 집합과 물리적 기준 프레임 간의 구별이 이루어져야 한다.그러한 구별에 대한 무지함은 많은 혼란의 원천이다. 예를 들어 속도와 같은 종속 함수는 물리적 기준 프레임에 대해 측정되지만 방정식이 지정된 수학적 좌표계를 자유롭게 선택할 수 있다.
또한 R과 [R, R, 등][7]의 구별에 대해서도 설명합니다.
기준 프레임의 개념은 좌표계의 개념과는 상당히 다릅니다.프레임은 다른 공간(휴대점 세트) 또는 시간(동시 이벤트 세트)을 정의할 때만 다릅니다.공간, 시간, 휴식, 동시성의 개념은 프레임의 개념과 불가분의 관계에 있습니다.그러나 단순히 원점 이동이나 공간 좌표가 완전히 공간적으로 회전하면 새로운 좌표계가 만들어집니다.따라서 프레임은 기껏해야 좌표계 클래스에 해당합니다.
그리고 J.D.로부터.Norton:[8]
특수 상대성 이론과 일반 상대성 이론의 전통적인 발전에서는 상당히 다른 두 가지 생각을 구별하지 않는 것이 관례였다.첫 번째는 좌표계의 개념으로, 단순히 시공간 근방의 사건에 4개의 숫자를 매끄럽게, 반전할 수 있는 할당으로 이해된다.두 번째 기준 프레임은 그러한 숫자를 할당하는 데 사용되는 이상화된 시스템을 말합니다. […] 불필요한 제한을 피하기 위해 우리는 이 배치를 운율의 개념과 분리할 수 있습니다.[…] 델의 목적에 있어서 특히 중요한 것은 각 기준 프레임이 시공간에서 발생하는 각 이벤트에서 일정한 운동 상태를 갖는 것입니다.[…] 특수 상대성 이론의 맥락에서 그리고 관성 운동의 기준 프레임으로 스스로를 제한하는 한, 관성 기준 프레임과 그것이 유도하는 관성 좌표계 사이의 차이에 거의 의존하지 않는다.이러한 편안한 상황은 특수 상대성 이론 내에서조차 비균일한 움직임의 기준 프레임을 고려하기 시작하면 즉시 중단된다.보다 최근에는 아인슈타인 취급의 명백한 모호성을 협상하기 위해 기준 프레임의 개념이 좌표계와 다른 구조로 다시 등장하고 있다.
이 논의는 Bading과 Castellani가 [9]단순한 시공간 좌표계를 넘어서는 것이다.일반화 좌표를 사용하는 좌표계의 확장은 양자장 이론, 고전 상대론적 역학, 양자 [11][12][13][14][15]중력의 해밀턴과 라그랑지안의 공식의[10] 기초가 된다.
좌표계
비록 "좌표계"라는 용어는 비기술적인 의미로 종종 사용되지만, "좌표계"라는 용어는 수학에서 정확한 의미를 가지며, 때로는 물리학자의 의미도 그러하다.
수학에서 좌표계는 기하학 또는 [16][17]대수학의 한 측면이며, 특히 다지관 특성(물리학, 구성 공간 또는 위상 공간)[18][19]이다.n차원 공간에서 점 r의 좌표는 단순히 n개의 [20][21]숫자의 순서 집합이다.
일반적인 바나흐 공간에서는 이러한 숫자가 푸리에 급수와 같은 함수 확장의 계수일 수 있습니다.물리적 문제에서는 시공간 좌표 또는 일반 모드 진폭일 수 있습니다.로봇 설계에서는 상대 회전 각도, 선형 변위 또는 [22]접합부의 변형일 수 있습니다.여기서는 이러한 좌표가 일련의 함수에 의해 데카르트 좌표계와 관련될 수 있다고 가정합니다.
여기서 x, y, z 등은 점의 n 데카르트 좌표입니다.이러한 기능이 주어진 경우 좌표 표면은 다음 관계에 의해 정의됩니다.
이러한 지표면의 교차점에 의해 좌표선이 정의됩니다.선택된 모든 점에서 그 점에서의 교차 좌표선에 대한 접선은 그 점에서의 기저 벡터 세트1 {e2, e, …, en}를 정의한다.즉,[23] 다음과 같습니다.
단위 길이로 정규화할 수 있습니다.자세한 내용은 곡선 좌표를 참조하십시오.
좌표 표면, 좌표 선 및 기준 벡터는 좌표계의 [24]구성요소입니다.기준 벡터가 모든 점에서 직교하는 경우 좌표계는 직교 좌표계입니다.
좌표계의 중요한 측면은 좌표계의 호 길이 ds를 [25]좌표로 결정하는 미터법 텐서ik g이다.
여기서 반복된 인덱스가 요약됩니다.
이러한 발언에서 알 수 있듯이 좌표계는 수학적인 구성체이며, 공리계의 일부이다.좌표계와 물리적 움직임(또는 현실의 다른 측면) 사이에 필요한 연결은 없습니다.그러나 좌표계는 시간을 좌표로 포함할 수 있으며 움직임을 설명하는 데 사용할 수 있습니다.따라서 로렌츠 변환과 갈릴레이 변환은 좌표 변환으로 볼 수 있다.
좌표계의 일반적이고 구체적인 토픽은 아래 링크도 참조할 수 있습니다.
물리
종종 물리적 기준 프레임, 기준 프레임 또는 단순히 프레임이라고 불리는 관찰 기준 프레임은 관찰자 및 관찰자의 운동 상태와 관련된 물리적 개념입니다.여기서 우리는 Kumar와 Barve에 의해 표현된 관점을 채택한다: 관찰 기준 프레임은 [26]그 운동 상태에 의해서만 특징지어진다.그러나 이 점에 대해서는 만장일치가 부족하다.특수상대성이론에서는 관찰자와 프레임을 구분하기도 한다.이 뷰에 따르면 프레임은 옵저버와 시간상 벡터에 수직인 공간상 벡터의 직교정규격자로 구성된 좌표격자가 된다.도란을 [27]봐이 제한된 견해는 여기서 사용되지 않으며, 상대성 [28][29]이론의 논의에서도 보편적으로 채택되지 않는다.일반 상대성 이론에서는 일반 좌표계를 사용하는 것이 일반적이다(예를 들어, 고립된[30] 구 바깥의 중력장에 대한 슈바르츠실트 해 참조).
관측 기준 프레임에는 관성 및 비관성 두 가지 유형이 있습니다.관성 기준 프레임은 모든 물리 법칙이 가장 단순한 형태를 취하는 프레임으로 정의됩니다.특수 상대성 이론에서 이러한 프레임은 속도에 의해 매개 변수화된 로렌츠 변환에 의해 관련됩니다.뉴턴 역학에서, 더 제한된 정의는 뉴턴의 제1법칙이 참이라는 것만을 요구한다. 즉, 뉴턴 관성 프레임은 자유 입자가 일정한 속도로 직선으로 이동하거나 정지해 있는 것을 말한다.이러한 프레임은 갈릴레오 변환과 관련이 있습니다.이러한 상대론적 변환과 뉴턴적 변환은 푸앵카레 군과 갈릴레오 군의 표현 측면에서 일반 차원의 공간으로 표현된다.
관성 프레임과 대조적으로 비관성 기준 프레임은 관측치를 설명하기 위해 가상의 힘을 호출해야 하는 프레임이다.예를 들어, 지구 표면의 한 점에 중심을 둔 관측 기준 프레임이 있습니다.이 기준 프레임은 코리올리 힘, 원심력, 중력으로 알려진 가공의 힘을 지구 중심 주위를 공전한다. (중력을 포함한 이 모든 힘은 자유 낙하 중 하나인 진정한 관성 기준 프레임에서 사라진다.)
측정기
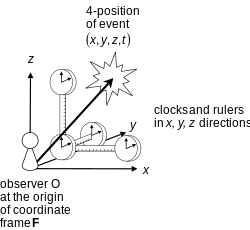
기준 프레임의 또 다른 측면은 프레임에 부착된 측정 장치(예: 시계 및 막대)의 역할입니다(위의 Norton 인용 참조).이 문제는 이 기사에서 다루지 않으며, 관찰자와 측정 사이의 관계가 아직 논의 중인 양자 역학에서 특히 관심이 있다(측정 문제 참조).
물리학 실험에서는 실험실 측정 장치가 정지해 있는 기준 프레임을 보통 실험실 프레임 또는 단순히 "실험 프레임"이라고 합니다.예를 들어 입자 가속기의 검출기가 정지해 있는 프레임이 있습니다.일부 실험에서 실험실 프레임은 관성 프레임이지만 반드시 관성 프레임일 필요는 없습니다(예를 들어 많은 물리학 실험에서 지구 표면의 실험실은 관성 프레임이러한 프레임은 관성 프레임이 아닙니다.입자물리학 실험에서는 에너지와 입자의 모멘타를 측정하는 실험실 프레임에서 COM 프레임에 존재하는 모든 운동 에너지가 새로운 입자를 만드는 데 사용될 수 있기 때문에 때때로 계산이 단순해지는 운동량 프레임의 중심 "COM 프레임"으로 변환하는 것이 종종 유용합니다.
이와 관련하여 관찰자의 측정 장비를 설명하는 데 자주 사용되는 시계와 막대는 실제로 진공의 성질에 연결된 훨씬 더 복잡하고 간접적인 도량형으로 대체되며 표준 모델에 따라 작동하며 g에 대해 보정해야 하는 원자 시계를 사용한다.중력 시간 [31]연장(두 번째, 미터 및 킬로그램 참조).
사실, 아인슈타인은 시계와 막대가 단지 편리한 측정 장치일 뿐이고 그것들은 예를 들어 원자와 [32]분자에 기반을 둔 보다 근본적인 실체에 의해 대체되어야 한다고 느꼈다.
인스턴스
- 기타 프레임
「 」를 참조해 주세요.
메모들
- ^ Kovalevsky, J.; Mueller, Ivan I. (1989). "Introduction". Reference Frames. Astrophysics and Space Science Library. Vol. 154. Dordrecht: Springer Netherlands. pp. 1–12. doi:10.1007/978-94-009-0933-5_1. ISBN 978-94-010-6909-0. ISSN 0067-0057.
- ^ 예를 들어, 다양한 시간과 길이 척도의 구성 관계를 사용하여 맥스웰 방정식에 들어가는 전류 및 전하 밀도를 결정하는 전자기학에서 거시적 프레임과 미시적 프레임의 차이는 나타납니다.예를 들어, 이러한 차이는 열역학에서도 나타납니다.를 참조해 주세요.
- ^ 매우 일반적인 조건에서 아크 자이의, 좌표 시스템은) 복잡한 거짓말 그룹에서 크시(t), 레프 Semenovich Pontri͡agin(1986년)를 참조하십시오.L.S. 폰트랴긴:SelectedWorksVol2:위상 기하학적 그룹(3판).고든과 균열. 우편 429.아이 에스비엔 2-88124-133-6..덜 추상적으로, n-dimensions의 공간에 좌표계를 기준 벡터{e1,e2,… 앙}의 집합의 있어서 에도아르도 Sernesi.J.Montaldi(1993년)정의된다.선형 대수학:기하학적 접근법이다.CRC프레스. p. 95.아이 에스비엔 0-412-40680-2.이와 같이, 이 좌표계는 수학 개념인, 운동과 관련이 있을 수 있는 언어가 없지만 necessa다.동작에 대한 ry conny
- ^ J X Zheng-Johansson; Per-Ivar Johansson (2006). Unification of Classical, Quantum and Relativistic Mechanics and of the Four Forces. Nova Publishers. p. 13. ISBN 1-59454-260-0.
- ^ Jean Salençon; Stephen Lyle (2001). Handbook of Continuum Mechanics: General Concepts, Thermoelasticity. Springer. p. 9. ISBN 3-540-41443-6.
- ^ Patrick Cornille (Akhlesh Lakhtakia, editor) (1993). Essays on the Formal Aspects of Electromagnetic Theory. World Scientific. p. 149. ISBN 981-02-0854-5.
{{cite book}}:author=범용명(도움말)이 있습니다. - ^ Nerlich, Graham (1994). What Spacetime Explains: Metaphysical essays on space and time. Cambridge University Press. p. 64. ISBN 0-521-45261-9.
- ^ 존 D. 노튼(1993)일반 공분산과 일반 상대성 이론의 기초: 80년간의 논쟁, Prog의원. 신체, 56페이지, 835-7
- ^ Katherine Brading; Elena Castellani (2003). Symmetries in Physics: Philosophical Reflections. Cambridge University Press. p. 417. ISBN 0-521-82137-1.
- ^ Oliver Davis Johns (2005). Analytical Mechanics for Relativity and Quantum Mechanics. Oxford University Press. Chapter 16. ISBN 0-19-856726-X.
- ^ Donald T Greenwood (1997). Classical dynamics (Reprint of 1977 edition by Prentice-Hall ed.). Courier Dover Publications. p. 313. ISBN 0-486-69690-1.
- ^ Matthew A. Trump; W. C. Schieve (1999). Classical Relativistic Many-Body Dynamics. Springer. p. 99. ISBN 0-7923-5737-X.
- ^ Alexander Solomonovich Kompaneyets (2003). Theoretical Physics (Reprint of the 1962 2nd ed.). Courier Dover Publications. p. 118. ISBN 0-486-49532-9.
- ^ M Srednicki (2007). Quantum Field Theory. Cambridge University Press. Chapter 4. ISBN 978-0-521-86449-7.
- ^ Carlo Rovelli (2004). Quantum Gravity. Cambridge University Press. p. 98 ff. ISBN 0-521-83733-2.
- ^ William Barker; Roger Howe (2008). Continuous symmetry: from Euclid to Klein. American Mathematical Society. p. 18 ff. ISBN 978-0-8218-3900-3.
- ^ Arlan Ramsay; Robert D. Richtmyer (1995). Introduction to Hyperbolic Geometry. Springer. p. 11. ISBN 0-387-94339-0.
geometry axiom coordinate system.
- ^ 호킹과 엘리스에 따르면, "다양체는 좌표 패치로 덮일 수 있다는 점에서 유클리드 공간과 국소적으로 유사한 공간이다.이 구조에서는 미분을 정의할 수 있지만 서로 다른 좌표계를 구분하지는 않습니다.따라서 다지관 구조에 의해 정의된 유일한 개념은 좌표계의 선택과 무관한 개념입니다."StephenW.Hawking은 조지 프랜시스 Rayner 엘리스(1973년).그 대형 구조 Space-Time.캠브리지 대학 출판부. 11p..아이 에스비엔 0-521-09906-4.수학적 정의:M의 각 지점은 유클리드의 다차원 공간에 개방된 집합에homeomorphic은 개방되어 집합에 포함되는 연결 하우스 도르프 공간 M은 다차원 다양체라고 불리는 것이었다.
- ^ Shigeyuki Morita; Teruko Nagase; Katsumi Nomizu (2001). Geometry of Differential Forms. American Mathematical Society Bookstore. p. 12. ISBN 0-8218-1045-6.
geometry axiom coordinate system.
- ^ Granino Arthur Korn; Theresa M. Korn (2000). Mathematical handbook for scientists and engineers : definitions, theorems, and formulas for reference and review. Courier Dover Publications. p. 169. ISBN 0-486-41147-8.
- ^ Encarta 정의를 참조하십시오.2009-10-31 아카이브 완료.
- ^ Katsu Yamane (2004). Simulating and Generating Motions of Human Figures. Springer. pp. 12–13. ISBN 3-540-20317-6.
- ^ Achilleus Papapetrou (1974). Lectures on General Relativity. Springer. p. 5. ISBN 90-277-0540-2.
- ^ Wilford Zdunkowski; Andreas Bott (2003). Dynamics of the Atmosphere. Cambridge University Press. p. 84. ISBN 0-521-00666-X.
- ^ A. I. Borisenko; I. E. Tarapov; Richard A. Silverman (1979). Vector and Tensor Analysis with Applications. Courier Dover Publications. p. 86. ISBN 0-486-63833-2.
- ^ 참조
- ^ 를 클릭합니다Chris Doran; Anthony Lasenby (2003). Geometric Algebra for Physicists. Cambridge University Press. p. §5.2.2, p. 133. ISBN 978-0-521-71595-9..
- ^ 예를 들어, 뮐러는 다음과 같이 말한다. "직교 좌표 대신에 우리는 분명히 물리적 공간에서의 점의 고정에 일반적인 곡선 좌표를 사용할 수 있다.…이제 일반적인 "직선" 좌표i x를 4공간으로 소개합니다….
- ^ A. P. Lightman; W. H. Press; R. H. Price; S. A. Teukolsky (1975). Problem Book in Relativity and Gravitation. Princeton University Press. p. 15. ISBN 0-691-08162-X.
relativistic general coordinates.
- ^ Richard L Faber (1983). Differential Geometry and Relativity Theory: an introduction. CRC Press. p. 211. ISBN 0-8247-1749-X.
- ^ Richard Wolfson (2003). Simply Einstein. W W Norton & Co. p. 216. ISBN 0-393-05154-4.
- ^ 를 참조해 주세요.


![{\displaystyle \mathbf {r} =[x^{1},\ x^{2},\ \dots ,\ x^{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7dd8270c4f5fa053e35aeab704c2d09b59e3275)








