BKL 특이점

이 기사는 대부분의 독자들이 이해하기에는 너무 전문적일 수 있다. 기술적인 세부사항을 삭제하지 않고 비전문가도 쉽게 이해할 수 있도록 개선해 주시기 바랍니다. (2016년 4월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

시리즈의 일부
물리 우주론
빅뱅 · 우주 우주의 나이 우주의 연대기
초기 우주 인플레이션 · 핵합성 배경 중력파(GWB) 전자레인지(CMB) · 중성미자(CNB)
확장·미래 허블의 법칙 · 레드시프트 공간의 메트릭 확장 FLRW 메트릭 · 프리드만 방정식 비균질 우주론 팽창하는 우주의 미래 우주의 궁극적 운명
구성품·구조 구성 요소들 람다-CDM 모형 암흑 에너지 · 다크 유체 · 암흑 물질 구조. 우주의 모양 은하 필라멘트 · 은하 형성 큰 퀘이사군 대규모 구조물 이온화 · 구조 형성
실험 블랙홀 이니셔티브(BHI) 부메랑 우주배경탐사기(COBE) 암흑 에너지 조사 일러스트리스 프로젝트 플랑크 우주 관측소 Sloan Digital Sky Survey (SDSS) 2dF Galaxy Redshift 조사 ('2dF') 윌킨슨 마이크로파 이방성 프로브(WMAP)
과학자 아론손 알펜 알퍼 바라드와이 코페르니쿠스 드 시터 다이케 엘러스 아인슈타인 엘리스 프리드만 갈릴레오 가모우 거스 호킹 허블 케플러 레마슈트르 마더 뉴턴 경이다. 펜로즈 펜지아 루빈 슈미트 스무트 선체프 수냐예프 톨만 윌슨 젤도비치 우주론자 목록
대상 이력 우주 마이크로파 발견 백그라운드 방사선 빅뱅 이론의 역사 종교적 해석 빅뱅 이론 우주론 연대표
카테고리 천문 포털
v t

BKL(Belinski-Khalatnikov-Lifshitz) 특이점은 초기 중력 특이점 근처에 있는 우주의 동적 진화의 모형으로, 아인슈타인 ^[2]중력장 방정식의 이방성, 혼돈한 해로 설명된다.이 모델에 따르면, 우주는 시간과 공간이 ^{[clarification needed]}0이 되는 중력 특이점 주변에서 요동치고 있다.이 특이성은 솔루션의 필수 특성이라는 점에서 물리적으로 실재하며, 이러한 방정식의 정확한 해에도 나타납니다.특이점은 프리드만-레미트르-로버톤-워커, 준등방성 및 카스너 솔루션과 같은 다른 특수 솔루션에 의해 만들어진 가정과 단순화에 의해 인위적으로 생성되지 않는다.

이 모델은 당시 란다우 이론 물리학 연구소에서 일하던 블라디미르 벨린스키, 이사크 칼라트니코프, 에브게니 리프시츠의 이름을 따서 명명되었다.

BKL이 개발한 사진에는 몇 가지 중요한 요소가 있습니다.다음과 같습니다.

• 특이점 근처에서는 서로 다른 공간점에서의 기하학적 진화가 분리되므로 적절히 정의된 공간 스케일 인자에 대한 시간에 관한 일반 미분 방정식의 해법에 의해 근사될 수 있다.이것은 BKL 추측이라고 불립니다.
• 대부분의 물질 유형에서 특이점 근처에서는 기하학의 역학에 대한 물질장의 영향이 무시할 수 있게 됩니다.존 휠러의 말을 빌리자면, 특이점에 가까운 "물질은 중요하지 않다"는 것이다.원래의 BKL 연구는 모든 물질에 무시해도 될 정도의 영향을 끼쳤지만, 나중에 그들은 질량 없는 스칼라 장에 해당하는 "질량 물질" (p = θ 상태)이 특이점 근처의 역학에 수정 영향을 미칠 수 있다는 이론을 세웠다.
• 점근성을 설명하는 일반 미분 방정식은 혼합 마스터 역학을 구성하는 공간적으로 균질한 해법, 즉 BKL에 의해 논의된 것과 유사한 특성을 나타내는 복잡한 진동 및 카오스 모형에서 비롯됩니다.

우주론적 특이점 근처의 우주의 역학 연구는 현대 이론과 수학 물리학의 빠른 발전 분야가 되었다.다차원(Kaluza-Klein 유형) 우주론 모델에서 BKL 모델의 우주론적 특이성에 대한 일반화는 한정된 수의 진동을 거친 후 우주가 단조로운 K로 들어가는 동안 차원수가 10 이하인 공간에서는 혼돈스러운 특성을 가진다.아스너형 체약 ^[3][4][5]체제

슈퍼스트링 모델에 기초한 우주론 연구의 발전은 특이점 근처에서 ^[6][7][8]역학의 몇 가지 새로운 측면을 밝혀냈다.이 모형에서 카스너 시대의 변화 메커니즘은 중력 상호작용이 아니라 존재하는 다른 장의 영향에 의해 유발된다.6개의 주요 초끈 모델과 D = 11개의 초중력 모델에 기초한 우주론 모델은 특이점을 향한 카오스 BKL 역학을 나타낸다는 것이 입증되었다.진동 BKL과 유사한 우주론 모델과 무한 차원 리 대수의 특별한 하위 클래스인 소위 쌍곡선 Kac-Moody ^[9][10][11]대수 사이에 연관성이 발견되었습니다.

서론

현대 우주론의 기초는 1922-1924년 알렉산더 프리드만이 발견한 아인슈타인 장 방정식의 특수 해법이다.우주는 균질(모든 점에서 동일한 메트릭 특성(측정값)을 갖는 공간)과 등방성(모든 방향에서 동일한 측정값을 갖는 공간)으로 가정됩니다.Friedmann의 솔루션은 공간에 대해 두 가지 가능한 기하학적 구조를 허용합니다. 즉, 볼처럼 바깥쪽으로 구부러진 공간(양곡률)을 가진 폐쇄형 모델과 안장처럼 안으로 구부러진 공간(음곡률)을 가진 개방형 모델입니다.두 모델 모두 우주는 정지하지 않고 끊임없이 팽창하거나 수축하거나 둘 중 하나입니다.이는 후퇴하는 은하의 허블 적색편이를 확립한 에드윈 허블에 의해 확인되었습니다.현재의 합의는 일반적으로 등방성 모델이 우주의 현재 상태에 대한 적절한 설명을 제공한다는 것입니다; 하지만, 현재 우주의 등방성 자체는 그것이 우주 진화의 초기 단계를 설명하기에 충분하다고 기대할 이유가 없습니다.동시에, 현실세계에서 동질성은 기껏해야 근사치에 불과하다는 것은 명백하다.은하간 공간에 비해 큰 거리에서의 물질 밀도의 균질한 분포에 대해 말할 수 있다고 해도, 이러한 균질성은 더 작은 규모로 사라집니다.반면, 동질성 가정은 수학적 측면에서 매우 멀리 간다. 즉, 보다 일반적인 경우를 고려할 때 사라지는 특정 특성을 부여할 수 있는 해답을 매우 대칭적으로 만든다.

등방성 모델의 또 다른 중요한 특성은 시간 특이성의 불가피한 존재입니다. 시간 흐름은 연속적이지 않지만 시간이 매우 크거나 매우 작은 값에 도달한 후에 멈추거나 반전됩니다.특이점 사이에서 시간은 한 방향으로 흐릅니다. 특이점(시간의 화살표)에서 멀어지는 것입니다.오픈 모델에는 시간 단수가 있어 한쪽 끝에는 시간이 제한되지만 다른 한쪽 끝에는 시간이 무제한인 반면, 클로즈드 모델에는 양 끝에는 시간을 제한하는 단수가 2개 있습니다(빅뱅과 빅 크런치).

(특이점과 같은) 공간 공간의 유일한 물리적으로 흥미로운 특성은 안정적인 특성, 즉 초기 데이터가 약간 교란되었을 때 여전히 발생하는 특성이다.특이점은 안정적이지만 물리적 관심이 없는 것이 가능하다. 안정성은 물리적 관련성을 위해 필요하지만 충분한 조건은 아니다.예를 들어, 특이점은 고도 이방성 우주에 해당하는 초기 데이터 집합 근처에서만 안정적일 수 있다.실제 우주는 현재 거의 등방성이기 때문에 우리 우주에서는 그런 특이점이 발생할 수 없다.안정적인 특이점이 물리적 관심사가 되기 위한 충분한 조건은 특이점이 일반(또는 일반)이어야 한다는 요건이다.대략적으로 말하면, 안정된 특이점은 초기 조건의 모든 집합 근처에서 발생하며 비중력장이 특정한 방식으로 "물리적으로 현실적인" 장으로 제한되어 아인슈타인 방정식, 다양한 상태 방정식 등이 진화된 공간 위에 유지된다고 가정할 경우 일반적이다.특이점은 실제 중력 자유도의 작은 변화에서 안정적이지만, 특이점은 어떤 식으로든 좌표계나, 오히려 시공간이 진화한 초기 초서면의 선택에 따라 달라지기 때문에 일반적이지 않을 수 있습니다.

아인슈타인 방정식과 같은 비선형 미분 방정식의 시스템에서는 일반 해법이 명확하게 정의되지 않습니다.원칙적으로 복수의 일반 적분이 존재할 수 있으며, 각각의 적분은 가능한 모든 초기 조건의 유한 부분 집합만을 포함할 수 있다.이러한 적분 각각은 일부 조건(예: 일부 불평등)의 영향을 받을 수 있는 모든 필수 독립 기능을 포함할 수 있다.따라서 특이점을 갖는 일반 해법의 존재는 특이점을 포함하지 않는 다른 추가 일반 해법의 존재를 배제하지 않는다.예를 들어, 상대적으로 질량이 작은 고립된 물체를 설명하는 특이점이 없는 일반 솔루션의 존재를 의심할 이유가 없다.

모든 공간과 시간에 대한 일반 적분을 찾는 것은 불가능하다.단, 이것은 문제를 해결하기 위해 필요한 것은 아닙니다.특이점에 가까운 솔루션을 연구하는 것으로 충분합니다.이것은 또한 문제의 또 다른 측면을 해결할 것이다: 리만 곡률 텐서의 물질 밀도와 불변성이 무한해지는 지점으로 이해되는 물리적 특이점에 도달했을 때 일반적인 해에서의 시공간 메트릭 진화의 특성.

물리적 시간 특이점의 존재

(BKL이 속한) 란다우 그룹에 의해 연구된 주요 문제 중 하나는 상대론적 우주 모델이 반드시 시간 특이점을 포함하는지 또는 시간 특이점이 이러한 모델을 단순화하기 위해 사용된 가정의 인공물인지 여부였다.대칭 가정에 대한 특이성의 독립성은 시간 특이성이 특별한 것뿐만 아니라 아인슈타인 방정식의 일반적인 해에도 존재한다는 것을 의미합니다.일반 해법에 특이점이 존재한다면, 아인슈타인 방정식의 가장 일반적인 특성에만 기초하는 몇몇 징후들이 있을 것이라고 제안하는 것은 타당하다. 그러나 그러한 징후들 자체는 특이점을 특징 짓는데 충분하지 않을 수 있다.

해법의 일반성에 대한 기준은 해법이 포함하는 독립적인 공간 좌표 함수의 수이다.여기에는 참조 프레임을 선택해도 수를 줄일 수 없는 "물리적으로 독립적인" 기능만 포함됩니다.일반적인 해법에서, 그러한 함수의 수는 초기 상태로 선택된 어떤 순간에 초기 조건(물질의 분포와 이동, 중력장의 분포)을 완전히 정의하기에 충분해야 한다.이 숫자는 빈(진공)^[12][13] 공간에 대해 4개, 물질 및/또는 방사선이 채워진 공간에 대해 8개입니다.

란다우 그룹의 ^[14][15][16]이전 연구 결과, 에서 검토한^[12] 결과, 일반적인 솔루션은 물리적 특이점을 포함하지 않는다는 결론을 도출했다.특이점을 가진 보다 광범위한 종류의 해법을 찾는 것은 아인슈타인 방정식의 연구에 대한 체계적인 접근이 부족했기 때문에 기본적으로 시행착오 방법에 의해 이루어졌다.이렇게 해서 얻을 수 있는 부정적인 결과는 그것만으로는 납득할 수 없다.필요한 범용성을 가진 해법은 무효가 되고 동시에 특정 해법과 관련된 긍정적인 결과를 확인할 수 있다.

그 당시에, 일반적인 솔루션에서 물리적 특이성의 존재에 대해 알려진 유일한 지표는 동기 프레임, 즉 적절한 시간⁰ x = t가 전체 공간에 걸쳐 동기화되는 프레임에 쓰여진 아인슈타인 방정식의 형태와 관련이 있었다; 이 프레임에서 공간 거리 요소 dl은 분리되었다.시간 간격 ^{[note 1]}dt.아인슈타인 방정식

${\displaystyle R_{0}^{0}=T_{0}^{0}-{\tfrac {1}{2}}T}$

(eq.1)

동기 프레임으로 작성된 결과는 물질 ^[12][13]분포에 대한 어떠한 가정에도 관계 없이 메트릭 결정식 g가 유한 시간 내에 불가피하게 0이 되는 결과를 제공합니다.

그러나 일반적인 물리적 특이점을 찾으려는 노력은 위에서 언급한 특이점이 동기 프레임의 특정 기하학적 특성, 즉 시간선 좌표의 교차와 연결되어 있다는 것이 명백해진 후에 사라졌다.이 교차는 기하학적 광학에서 가성 표면의 4차원 유사인 일부 포위 하이퍼서페이스에서 발생합니다. 이 ^[16]교차점에서 g는 정확히 0이 됩니다.따라서 이 특이점은 일반적이지만 물리적인 특이점이 아닌 가공의 것입니다.기준 프레임이 변경되면 사라집니다.이것은 분명히 연구자들이 이러한 방식으로 더 많은 조사를 하도록 설득했다.

이 문제에 대한 관심이 다시 고조되기 몇 년이 지난 후 펜로즈(1965)가 미지의 성격의 특이점의 존재를 기준 프레임의 선택과 공통점이 없는 매우 일반적인 가정과 연관짓는 그의 이론을 발표했을 때 다시금 고조되었다.나중에 호킹과^[19] 게록에 의해^[17][18] 비슷한 다른 이론들이 발견되었다(펜로즈 참조).호킹 특이점 정리).이것은 단일한 해결책을 찾는 것에 대한 관심을 다시 불러일으켰다.

범용 동종 솔루션

균질하고 등방성이 있는 공간에서는 메트릭이 완전히 결정되어 곡률 부호만 자유롭게 남습니다.등방성과 같은 추가 대칭이 없는 공간 동질성만 가정하면 메트릭 선택에 상당한 자유를 남긴다.다음은 동기 프레임을 가정한 특정 순간 메트릭의 공간 부분에 관한 것으로, t는 공간 전체에 대해 동일한 동기 시간입니다.

BKL 추측

1970년 연구에서,^[2] BKL은 특이점에 접근할 때, 아인슈타인의 방정식에서 시간 미분을 포함하는 항이 공간 미분을 포함하는 항보다 우세하다고 말했다.이것은 이후 BKL 추측으로 알려져 왔고 아인슈타인의 편미분방정식(PDE)은 일반상대성이론의 역학이 효과적으로 국소적이고 진동하는 상미분방정식에 의해 잘 근사된다는 것을 암시한다.각 공간 지점에서 필드의 시간 진화는 비앙치 분류의 균질 우주론에 의해 잘 근사된다.

예를 들어 아인슈타인 방정식의 시간과 공간 도함수를 동질 공간의 분류에 사용하는 방법으로 분리한 후 공간 도함수를 포함하는 항을 0으로 설정함으로써 시스템의 소위 잘린 이론(삼분할 ^[20]방정식)을 정의할 수 있다.다음으로 BKL 추측을 보다 구체적으로 할 수 있습니다.

약한 추측:특이점에 접근함에 따라 아인슈타인 방정식의 공간 도함수를 포함하는 항은 시간 도함수를 포함하는 항에 비해 무시할 수 있습니다.따라서 특이점에 접근할 때 아인슈타인 방정식은 미분 항을 0으로 설정하여 구한 방정식에 접근합니다.따라서, 약한 추측은 아인슈타인 방정식이 특이점 근처에서 잘린 방정식에 의해 잘 근사될 수 있다고 말한다.이는 전체 운동 방정식의 해법이 특이점에 접근함에 따라 잘린 방정식의 해법에 접근한다는 것을 의미하지는 않는다는 점에 유의하십시오.이 추가 조건은 다음과 같이 strong 버전에서 캡처됩니다.

강한 추측:특이점에 접근함에 따라 아인슈타인 방정식은 잘린 이론의 방정식에 접근하고, 게다가 완전 방정식에 대한 해는 잘린 방정식에 대한 해로 근사된다.

처음에 BKL 추측은 좌표 의존적이고 다소 믿을 수 없는 것처럼 보였다.예를 들어 Barrow와 Tipler는 ^[21][22]BKL 연구의 10가지 비판 중 시간과 공간의 파생물을 분리하는 수단으로서 (그들에 따르면) 동기 프레임의 부적절한 선택을 포함한다.BKL 추측은 때때로 문헌에서 시간 미분만이 특이점 근처에서는 중요하다는 진술로 바꿔 표현되었다.이러한 진술은 액면 그대로 받아들여지는 것으로 잘못되었거나 기껏해야 BKL 분석 자체에서 보여지듯이 4개의 시공간 차원에서의 순수한 아인슈타인 중력의 일반 해법에서 미터법 텐서의 공간적 구배를 무시할 수 없고, 실제로 진동 정체의 출현에 중요한 역할을 하기 때문이다.그러나 아인슈타인 이론의 재구성은 관련된 구배를 포함하는 새로운 변수, 예를 들어 시간 도함수의 지배적 역할에 대한 진술이 ^[20]올바른 아슈테카 유사 변수와 같은 측면에서 존재한다.각 공간 지점에서 시간에 관한 일반 미분 방정식에 의해 기술된 유한 차원 동적 시스템의 관점에서 특이성에 대한 효과적인 설명을 얻는 것은 사실이지만, 공간 구배는 이러한 방정식에 비삼중적으로 들어갑니다.

다수의 저자에 의한 후속 분석은 BKL 추측이 정밀하게 이루어질 수 있다는 것을 보여주었고,^[23] 지금쯤이면 그 뒷받침에는 인상적인 수치적 및 분석적 증거가 있다.우리가 아직 강력한 추측의 증거와는 거리가 멀다고 말해도 무방하다.그러나 단순한 모델에서는 현저한 진전이 있었습니다.특히 버거, 가핑클, 몽크리프, 이센버그, 위버 등은 모형의 클래스에서 아인슈타인 장 방정식의 전체 해법에 접근함에 따라 공간 ^{[23][24][25][26][27]}도함수를 무시하여 얻은 "속도 항 지배"(절단)에 근접한다는 것을 보여주었다.앤더슨과 렌달은^[28] 질량이 없는 스칼라장이나 단단한 유체에 결합된 중력의 경우, 잘린 방정식의 모든 해에는 대칭이 없는 경우에도 특이점이 접근함에 따라 잘린 해로 수렴되는 전체 장 방정식에 대한 해답이 존재한다는 것을 보여주었다.이러한 결과는 p-form 게이지 ^[29]필드도 포함하도록 일반화되었다.이러한 잘린 모형에서는 역학이 더 단순하여 입증될 수 있는 추측에 대한 정확한 진술을 가능하게 한다.일반적인 경우, 지금까지의 가장 강력한 증거는 수치적 진화에서 나온다.Berger와^[30] Moncrief는 일반적인 우주론적 특이점을 분석하는 프로그램을 시작했다.초기 연구는 대칭성을 ^[31]감소시키는 사례에 초점을 맞췄지만, 최근에는^[32] Garfinkle이 대칭성이 없는 시공간 수치적 진화를 수행했는데, 이 경우에도 믹스마스터의 동작이 뚜렷하다.마지막으로, 슈바르츠실트 ^[33]블랙홀의 특이점 근처의 시험장 거동에 대한 수치적 연구로부터 추측에 대한 추가적인 뒷받침이 나왔다.

카스너 용액

이방성(등방성) 균질 공간에 대한 BKL 접근법은 공간이 균질하고 카스너 메트릭에 따라 시간에 의존하는 유클리드 메트릭을 갖는 진공의 장에 대해 카스너가^[34] 도출한 정확한 특정 솔루션의 일반화에서 시작한다.

${\displaystyle dl^{2}=t^{2p_{1}}+t^{2p_{2}+t^{2}+t^{2p_{3}}dz^{2}}$

(eq.2)

(dl은 선 요소이고, dx, dy, dz는 3개의 공간 차원에서의 극소 변위이며, t는 일부 초기₀ 모멘트 t = 0 이후 경과된 시간 주기이다.여기서₁ p, p₂, p는₃ 다음 카스너 조건을 만족시키는 세 가지 숫자입니다.

${\displaystyle p_{1}+p_{2}+p_{3}=p_{1}^{2}+p_{2}^{2}+p_{3}^{2}=1.}$

(eq.3)

이러한 관계 때문에 3개의 숫자 중 1개만 독립적입니다(3개의 미지수가 있는 2개의 방정식).3개의 숫자 모두 동일하지 않습니다.두 숫자는 값$$세트$(-13\frac{\mathrm{}}{}$, $2\frac{\mathrm{}}{}\frac{3}{}$, $\frac{2}{}$3 $)(\textstyle(-{\frac {1}{3}},${\$frac {2}{3}}}$ 및$$ (0, 0,^{[note 3]} 1)에서만 동일합니다.다른 모든 경우 숫자는 다르며, 한 숫자는 음수이고 다른 두 숫자는 양수입니다.이는 첫 번째 조건 eq.3의 양쪽을 제곱하고 정사각형을 전개함으로써 부분적으로 입증된다.

$\displaystyle \left(p_{1}+p_{2}+p_{3)}\right)^{2}=\left(p_{1}^{2}+p_{2}}^{2}+p_{3}^{2}\right)+\left(2p_{1}p_{2}+2p_{2}p_{3}+2p_{1}p_{3}\right)=1}$

용어$({\displaystyle }$ ${\displaystyle {p\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$2 + ${\displaystyle {p\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$2 + ${\displaystyle {p\mathrm{}}_{}^{}}$ 3${\displaystyle {}_{}^{}{\mathrm{}}_{}^{}}$ $){$ $displaystyle \left (p_{1}^{2}+p_{2$$}^{2}+p_{3$$}^{2}\$right$$)}은(는) 두 번째 조건 eq.3의 dint에 의해 1과 같으므로 혼합곱이 있는 항은 0이어야 한다.이는₁ p₂, p₃, p 중 적어도 하나가 음수인 경우에 가능합니다.

숫자가 오름차순으로₂₃ 배열되어 있으면₁ p < p < p 는 간격에 따라 변화한다(그림4).

${\displaystyle {tfrac {1}{3}}\leq p_{1}\leq 0,\leq p_{2}\leq {3},\{\frac {2}{3}}\leq p_{3}\leq 1.end}.$

(eq.4)

Kasner 미터법 eq. 2는 모든 부피가 시간에 따라 증가하는 평탄한 균질하지만 이방성 공간에 해당하며, 두 축 y와 z를 따르는 선형 거리는 증가하고 축 x를 따르는 거리는 감소한다.모멘트 t = 0은 용액에 특이점을 유발하며, t = 0에서 메트릭의 특이점은 기준 프레임 변환에 의해 피할 수 없습니다.특이점에서 4차원 곡률 텐서의 불변량은 무한대로 간다.예외는₁ p = δ₂ = 0, δ₃ = 1입니다. 이러한 값은 평탄한 시공간에 해당합니다. 변환 t sh z = δ, t ch z = δ는 카스너 메트릭(예. 2)을 갈릴레이로 변환합니다.

BKL은 다음과 같이 단일 독립(실제) 파라미터 u(Lifshitz-Khalatnikov 파라미터^[35])의 관점에서 숫자₁ p, p₂, p를₃ 파라미터화한다.

${\displaystyle p_{1}(u)=param frac {-u}{1+u+u^{2}}}}},\ p_{2}(u)=paramfrac {1+u}{1+u+u^{2}}}}},\ p_{3}(u)=paramfrac {u(1+u)}{1+u+u^{2}}}}}$

(eq. 5)

카스너 지수 모수화는 지수에 대한 두 가지 제약조건(예: Q.3)을 고려할 때까지 미스터리해 보인다. 두 제약조건 모두 지수의 전체 척도를 고정시켜 비율만 달라질 수 있다.이러한 비율 중 하나를 새로운 매개변수로 선택하는 것은 자연스러운 일이며, 이는 6가지 다른 방법으로 수행될 수 있습니다.예를 들어 u₃₂ = u₃ = p / p를₂ 선택하는 것은 6가지 가능한 비율을 모두 나타내는 것은 간단하다.p = up을₂ 먼저 제거한₃ 다음 선형 제약 조건을 사용하여 p = 1 - p₂ - up₂ = 1 - (1 + u)p를₂ 제거하면₁ 2차 제약 조건은 p의₂ 2차 방정식으로 감소합니다.

$\displaystyle \left [1+u\right]p_{2}\right]^{2}+p_{2}^{2}+\left(위_{2}\오른쪽)^{2}=1}$

(예. 5a)

루트₂ p = 0 (표준) 및₂ p = (1 + u) / (1 + u² + u)를 사용하여 p와₁₃ p를 역치환으로 구한다.(c, b_a, a)가 (1, 2, 3)^[36]의 순환 순열일 때 p ≤ p_b ≤ p ≤ p ≤ p인_ca 6개의_b 그러한 매개변수를_ab 정의할 수 있다.

u running 1의 범위에서 u를 실행한 상태에서 위와 같이 정렬된 p, p₂, p의₃ 모든₁ 다른 값을 구한다.u < 1 의 값은, 다음에 따라서 이 범위에 포함됩니다.

$\displaystyle p_{1}\frac {u}\right)=p_{1}(u),\p_{2}\left\frac {1}{u}\right)=p_{3}(u},\p_{3}\leftfrac {1}{u}\right)=p_{2}(u}$

(eq.6)

일반화 솔루션에서, eq.2에 해당하는 형태는 t의 거듭제곱에 의한 직렬 팽창의 주요 항에 각각 점근 측정 기준(특이점 t = 0에 가까운 측정 기준)에만 적용된다.동기 기준 프레임에는 공간 거리 요소가 포함된 eq.1 형식으로 쓰여 있습니다.

$\displaystyle dl^{2}=\left(a^{2}l_{\alpha}l_{\alpha}l_{\alpha}m_{\alpha}m_{\alpha}n_{\alpha}n_{\alpha}n_{\right}\left}ma^{\alpha}\left}lfilfilfilfilfilfilter }$

(eq.7)

어디에

$\displaystyle a=t^{p_{l},\b=t^{p_{m},\c=t^{p_{n}}}$

(eq.8)

3차원 벡터 l, m, n은 멱함수 법칙(예: 8)에 의해 시간과 함께 공간 거리가 변화하는 방향을 정의한다.이들 벡터는 이전과 마찬가지로 eq.3과 관련된 숫자_l p, p_m, p와_n 마찬가지로 공간 좌표의 함수이다.거듭제곱_l p, p_m, p는_n 오름차순으로 배열되지 않으며, eq. 5에서 오름차순으로 배열된 숫자에 대해 기호₁ p, p₂, p를₃ 예약한다.eq.7의 측정지표의 결정요인은 다음과 같다.

${\displaystyle -g=a^{2}b^{2}c^{2}v^{2}=t^{2}v^{2}}$

(예 9)

여기서 v = l[mn]입니다.다음과 같은 수량을 도입하는 것이 편리하다.

$\displaystyle \mathbf {l} \mathbf {l} \mathbf {l} {v} , \mu = specfrac {mathbf {m} \mathrm {f} {v} , \nu = specfrac {mathbf {l} \mathbf {l} \mathbf {v} \mathrm} \m}}$

(예 10)

eq. 7의 공간 메트릭은 eq. 8의 t의 거듭제곱은 동일한 값을 가질 수 없기 때문에 이방성이다.t = 0에서 특이점에 접근할 때, 각 공간 요소의 선형 거리는 두 방향으로 감소하고 세 번째 방향으로 증가한다.원소의 부피는 t에 비례하여 감소합니다.

캐스너 메트릭은 ^{[note 1]}eq. 7의 각 메트릭 텐서 θ를_αβ t의 a, b, c 의존성을 정의하지 않고 대입함으로써 아인슈타인 방정식에 도입된다.

$\displaystyle \varkappa _{\alpha }^{\alpha } = explac {2gldot {a}} l^{\alpha} + {\frac {2gldot {b}} {b}} m^{\alpha } + {\alpha } {\frac2gl^{c} {c} } {c} {c} } {c} }$

여기서 기호 위의 점은 시간에 따른 차이를 나타냅니다.아인슈타인 방정식 eq. 11은 다음과 같은 형태를 취한다.

${\displaystyle -R_{0}^{0}=harbfrac {ddot {a}}+{b}+{\frac {dot {c}}=0.}$

(eq.14)

모든 항은 큰 (t → 0) 수량 1/t에 대해 두 번째 차수가 됩니다.아인슈타인 방정식 eq. 12에서 그러한 순서의 항은 시간 미분된 항에서만 나타난다.P의 성분이_αβ 두 개보다 큰 주문 조건을 포함하지 않는 경우,

${\displaystyle -R_{l}^{l}=flac {(\dot {a}bc){\dot {}=0,\-R_{m}^m}=flac {{c}{\dot {b}}{c}}=0,\R_{n}{m}}=flac {dot}{frac}{{c}}}}}{frac}}{{{{{{c}}}}}}}}}}}}}}{fl}}}}}}}{flac}$

(eq.15)

여기서 지수 l, m, n은 l, m, ^[12]n 방향의 텐서 성분을 나타낸다.이러한 방정식은 eq.14와 함께 eq.3을 만족하는 검정력을 갖는 eq.8을 나타낸다.

그러나 3제곱 p_m, p_n, p 중_l 하나의 음의 거듭제곱이 존재하면 p에서_αβ t보다 큰 차수의⁻² 항이 나타납니다.음의 검정력이 p(p_l = p₁ < 0)이면_l P는_αβ 좌표 함수 θ를 포함하며 eq.12는

${\displaystyle {begin{aligned}-R_{l}^{l}&=frac {{\dot {a}}{\dot {}}+{\frac {\dot da ^{2}a^{2}}{2b^{2}}=0,\-R_{m^{l}}&frac {frac}{{{{{frac}}}}}}}}\\\end {aligned}}$

(eq.16)

여기서 두 번째 항은 p + p_n - p_l = 1 + 2 p_l > ^{[note 5]}1의_m 차수^{−2(p_m + p_n − p_l)} t이다.이러한 항을 제거하고 메트릭 eq. 7을 복원하려면 좌표 함수에 조건 θ = 0을 적용해야 한다.

나머지 3개의 아인슈타인 방정식 eq.13은 미터법 텐서의 1차 시간 도함수만 포함한다.그들은 eq.7의 좌표 함수에 필요한 조건으로 부과되어야 하는 세 가지 시간 독립적 관계를 제공한다.이것은 조건 θ = 0과 함께 4가지 조건을 만든다.이러한 조건은 10개의 다른 좌표 함수를 결합한다: 각 벡터 l, m, n의 3개의 성분과 t의 거듭제곱으로 하나의 함수(조건_l eq.3에 의해 결합되는 함수 p, p_m, p 중 하나_n).물리적으로 임의의 함수의 수를 계산할 때는 여기서 사용하는 동기 시스템이 3개의 공간 좌표를 시간에 의존하지 않는 임의의 변환이 가능함을 고려해야 합니다.따라서 최종용액에는 진공상태에서 일반용액에 필요한 것보다 1개 적은 10 - 4 - 3 = 3개의 물리적 임의함수가 포함되어 있다.

이 지점에 도달하는 일반성의 정도는 물질을 도입해도 감소하지 않는다. 물질은 메트릭 eq. 7에 기록되며 밀도의 초기 분포와 속도의 세 가지 성분을 설명하는 데 필요한 네 가지 새로운 좌표 함수를 제공한다.이것은 단순히 유체역학 방정식인 주어진 중력장에서 물질의 움직임의 법칙으로부터 물질의 진화를 결정하는 것을 가능하게 합니다.

${\displaystyle {\frac {1}{\fracrt {-g}}{\frac x^{i}}\leftfcrt {-g}}\frac u^{i}\right}=0,}$

(eq.17)

$(\displaystyle (p+\varepsilon)u^{k}\left\{\frac u_{i}{\frac x^{k}}-{\frac {1}u^{l}{\frac g_{i}{\frace}{\frace x{k}})u^{\frac {\frac}{\frac}{\frac}$

(eq.18)

여기서ⁱ u는 4차원 속도, θ 및 θ는 물질의 에너지 밀도 및 엔트로피입니다(cf. 및;^[38] 자세한 내용은 참조).^[39]상태 p = δ/3의 초잠재론적 방정식의 경우 엔트로피 δ ~ δ이다^1/4.규칙 17과 규칙 18의 주요 용어는 시간 파생물을 포함하는 용어이다.eq.17과 eq.18의 공간 구성요소로부터

$(\displaystyle {\frac t}\left\fracrt {-g}u_{0}\varepsilon ^{\frac {3}{4}\right)=0,\varepsilon \cdot {\frac u_{\alpha }{\frac t}}}}\cdpraccdfraphot \frcdprcd.$

결과적으로

${\displaystyle abcu_{0}\varepsilon ^{\frac {3}{4}=\mathrm {const},\u_{\alpha}\varepsilon ^{\frac {1}{4}=\mathrm {const},}$

(eq.19)

여기서 'const'는 시간에 구애받지 않는 수량이다.또한 uu_iⁱ = 1의 항등식에서 (u의 모든_α 공변량 성분이 동일한 순서에 있으므로)

$({displaystyle u_{0}^{n}\approx u_{n} u^{n} = scfrac {u_{n}^2}} {c^{2}} ).$

여기서_n u는 t의 최고(양) 동력으로 연결된 n의 방향에 따른 속도 성분이다(p_n = p라고₃ 가정).상기의 관계로부터 다음과 같다.

$\displaystyle \varepsilon \sim \frac {1}{a^{2}b^{2}},\u_{\alpha}\sim {b}}$

(eq. 20)

또는

$\displaystyle \varepsilon \sim t^{-2(p_{1}+p_{2})=t^{-2(1-p_{3}),\u_{\alpha}\sim t^{(1-p_{3}}}{2}}.}$

(eq.21)

위의 방정식은 물질의 응력-에너지-운동량 텐서가 방정식의 오른쪽에 있는지 확인하기 위해 사용될 수 있다.

${\displaystyle R_{0}^{0}=T_{0}^{0}-{\frac {1}{2}}T,\R_{\alpha}^{\alpha}=T_{\alpha}^{\alpha}{\frac {1}{2}}\frac_{\frac}{\frac}{\frac}T,\frash}T,}$

실제로는 왼쪽의 주요 항보다 1/t 낮은 차수입니다.$식{\displaystyle {}_{}^{}}$ 중 ${\displaystyle R_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ 0 $=$ ${\displaystyle T_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$0 {\$displaystyle R_{\alpha$}^{0}=$T_{\alpha$}^{$0}:$ 물질의$$ 존재는 구성 좌표 ^[12]함수에 부과되는 관계 변화만을 초래한다.

eq. 21의 법칙에 의해 θ가 무한이 된다는 사실은 eq. 7의 해법에서 오직 (0₂₃, 0, 1)을 제외한 모든 거듭제곱₁ p, p, p의 값에서 물리적 특이점을 다루고 있음을 확인시켜 준다.이러한 마지막 값의 경우 특이점은 비물리적이며 기준 프레임을 변경하여 제거할 수 있습니다.

검정력(0, 0, 1)에 대응하는 허구의 특이점은 타임라인 좌표가 2차원 "초점 표면"을 가로지르는 결과로 발생합니다.에서 ^[12]지적한 바와 같이 동기 기준 프레임은 (3차원 가성 표면이 아닌) 이러한 표면에서 정확히 이러한 불가피한 타임라인 교차가 발생하도록 항상 선택할 수 있다.따라서 공간 전체에 대해 이와 같은 동시성을 갖는 해는 일반 해법에 필요한 모든 임의 함수 집합과 함께 존재해야 한다.점 t = 0에 가까울 때 t의 전승만큼 규칙적으로 확장할 수 있습니다.이 케이스의 분석에 대해서는,^[41] 을 참조해 주세요.

특이점을 향해 진동 모드

일반적인 해법은 정의상 완전히 안정적이다.그렇지 않으면 우주가 존재하지 않을 것이다.어떤 섭동도 어떤 순간의 초기 조건의 변화와 동일하다.일반 해법은 임의의 초기 조건을 허용하기 때문에 섭동은 그 특성을 변경할 수 없다.이러한 각도로 볼 때, 솔루션 eq. 7의 좌표 함수에 부과되는 4가지 조건은 서로 다른 ${\displaystyle {유형}_{}^{}}$이다. 즉, R$$ 0 {\$displaystyle R_${\alpha $}^0$} $=$ 0에서 발생하는 3가지 조건은 "자연적"이며 아인슈타인 방정식의 결과이다.그러나 하나의 미분함수의 손실을 야기하는 추가 조건 θ = 0은 완전히 다른 유형이다: 섭동에 의해 야기된 불안정성은 이 조건을 깨트릴 수 있다.그러한 섭동의 작용은 모델을 다른 보다 일반적인 모드로 만들어야 한다.섭동은 작게 간주할 수 없습니다.새로운 모드로의 이행은 매우 작은 섭동의 범위를 초과합니다.

BKL에 의해 수행된 섭동 작용 하에서의 모델의 거동 분석은 ^{[2][42][43][44]}특이점에 접근할 때 복잡한 진동 모드를 묘사합니다.일반적인 케이스의 넓은 틀에서 이 모드의 모든 세부사항을 설명하지는 못했습니다.그러나 BKL은 광범위한 분석 연구를 허용하는 특정 모델에서 솔루션의 가장 중요한 특성과 특성을 설명했습니다.

이러한 모델은 특정 유형의 균질 공간 메트릭을 기반으로 합니다.추가 대칭 없이 공간의 동질성을 가정하면 측정 기준을 선택할 수 있는 큰 자유를 남긴다.Biancchi에 따르면 가능한 모든 균질(그러나 이방성) 공간은 여러 Biancchi 유형(타입 I - [45]IX)으로 분류됩니다.(일반화 균질해 참조) BKL은 Biancchi Type VII와 IX의 공간만을 조사한다.

메트릭이 eq.7의 형태를 갖는 경우, 각 균질 공간 유형에 대해 기준 벡터 l, m, n과 공간 좌표 사이에 함수 관계가 존재한다.이 관계의 구체적인 형태는 중요하지 않다.중요한 사실은 타입 VIII 및 IX 공간의 경우 수량 θ, μ, θ eq. 10은 상수이며, "혼합" 제품 l은 모두 썩는 m, l 로트 n, m 로트 l 등이다.0 입니다.타입 IX 공간의 경우, 양 μ, μ는 부호가 같고 = μ = = = 1로 쓸 수 있다(3개의 상수의 동시 부호 변경은 아무것도 바꾸지 않는다).타입 VII 공간의 경우, 2개의 상수는 세 번째 상수의 부호와 반대되는 부호를 가집니다. 예를 들어, δ = - 1, μ = μ = ^{[note 6]}= 1로 쓸 수 있습니다.

따라서 섭동이 "캐스너 모드"에 미치는 영향에 대한 연구는 아인슈타인 방정식의 γ 함유 항에 대한 연구로 제한된다.유형 VII 및 IX 공간이 이러한 연구에 가장 적합한 모델입니다.이들 Biancchi 타입의 3량 θ, μ, θ는 모두 0과 다르기 때문에 어느 방향 l, m, n이 음의 멱함수법칙 시간 의존을 가지든 조건 θ = 0은 유지되지 않는다.

타입 VIII 및 타입 IX 우주 모델의^{[46][note 1]} 아인슈타인 방정식은 다음과 같습니다.

${\displaystyle{\begin{정렬}-R_{나는}^{나는}&, ={\frac{\left({\dot{}}bc\right){\dot{}}}{abc}}+{\frac{1}{2}}\leftᆪ\left[\lambda ^{2}a^{4}-\left(\mu b^{2}-\nu c^{2}\right)^{2}\right]=0,\\-R_{m}^{m}&, ={\frac{(한{\dot{b}}c){\dot{}}}{abc}}+{\frac{1}{2}}\left(a^{2}b^{2}c^{2}\right)\left는 경우에는 \mu ^{2}b^{4}-\left(\lambda a^{2}-\n.uc^{2}\right)^{2}\right]=0,\-R_{n}^{n}&=frac {left(ab(도트 {c}\right){\dot {}{frac}+{\frac {1}{2}c{2}\left(a^{}\right)\[\nu ^2\c}{4}$

(eq.22)

${\displaystyle - R_{0}^{0}=harbfrac {a}}+{\frac {ddot {b}}+{\frac {c}}=0}$

(eq.23)

(나머지 $컴포넌트{\displaystyle {}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}${$style$ $R_{l}^$$0$ $R{\displaystyle {}_{}^{}}$ m$$${\displaystyle {\mathrm{}}_{}^{}}$ {${\displaystyle {\mathrm{}}_{}^{}}$ $R_$${n$$}^$$0$}, R l $m${$displaystyle{\displaystyle {}_{}^{}}$ $R_{l}^$$0$$\},$ $R{\displaystyle {}_{}^{}}$$$ {$displaystyle R_{l$}^{n$}),$ R m$${$displaystyle$$\},$이러한 방정식은 시간의 함수만을 포함합니다.이것은 모든 균질한 공간에서 충족되어야 하는 조건입니다.여기서 eq.22와 eq.23은 정확하며, 유효성은 t = ^{[note 7]}0에서 특이점에 얼마나 가까운지에 따라 달라지지 않는다.

eq.22와 eq.23의 시간 도함수는 로그 α, β, θ로 치환되는 경우 보다 단순한 형태를 취한다.

${\displaystyle a=e^{\alpha},\b=e^{\displays},\c=e^{\displays}}$

(eq.24)

다음과 같이 변수 t를 θ에 대입한다.

$\displaystyle dt=display\d\displays .}$

(eq.25)

다음으로 (아래 첨자는 )에 의한 차이를 나타냅니다).

${\displaystyle {displaystyle }2\alpha _{\mu b^{2}-\nu c^{2}\right}^2}-\displayda ^{2}-\displayda ^{4}=0,\displaystyle \=left(\displayda a^{2}-right)^{2}^{2}$

(eq.26)

${\displaystyle {1}{2}}\left(\alpha +\displays \right)_{\displays }=\alpha _{\displays }\displays }+\alpha _{\displays }+\displaysycright _{\dge }\displays}$

(eq.27)

방정식 eq.26을 더하고 eq.27에 따라 왼쪽의 합(α + β + _{τ τ}θ)을 대입하면 시스템 eq.26의 첫 번째 적분인 첫 번째 도함수만을 포함하는 방정식을 얻을 수 있다.

$\displaystyle \alpha _{\display}+\alpha _{\display}\display_{\display}+\display_{\display}=displayfrac {1}{4}\left(\displayda ^{4}+\mu ^2} ^{c} ^{\nu}}$

(eq.28)

이 방정식은 eq.26의 초기 상태에 부과되는 결합 조건의 역할을 한다.카스너 모드 eq. 8은 오른쪽의 모든 용어를 무시하는 경우 eq. 26의 해법이다.그러나 이러한 상황은 (t → 0에서) 무한히 지속될 수 없다. 왜냐하면 이러한 조건들 중에는 항상 일부만 증가하기 때문이다.따라서, 음의 힘이 함수 a(t)(p₁ = p)에_l 있다면, 카스너 모드의 섭동은 항 θa에²⁴ 의해 발생하며, 나머지 항은 t가 감소함에 따라 감소한다.증가하는 용어만 eq.26의 오른쪽에 남겨진 경우, 다음과 같이 시스템을 얻는다.

${\displaystyle \alpha } =-{\frac {1}{2}\flac ^{4\alpha}},\\flac _{\flac \alpha } =\flac {1}{4\flac } =\flac {1}{4\alpha } =\facclac ^{2}$

(eq.29)

(단, eq.16. 그 아래는 λ² = 1로 치환한다.)이러한 방정식의 해는 초기 상태로부터의 미터법 진화를 설명해야 한다. eq 8은 주어진 검정력 집합(p_l < 0)으로 설명한다. p = ,, p = ,, p_mn = so₁₂, p = so로₃ 하여 다음과 같이 한다_l.

$\displaystyle a\sim t^{p_{1},\b\sim t^{p_{2},\c\sim t^{3}.}$

(eq.30)

그리고나서

${\displaystyle abc=\Lambda t,\lambda =\Lambda ^{-1}\ln t+\mathrm {const}}$

(eq.31)

여기서 δ는 상수입니다.eq.29의 초기 조건은 다음과 같이 재정의된다.

$\displaystyle \alpha _{\lambda p_{1},\lambda p_{2},\lambda p_{3}\mathrm {at}\lambda p_{1}\lambda p_{1}\lambda p_{\infty}\t}\lam \to \lam \lam \lam \lam \lam \lam \lambt}$

(eq.32)

방정식 eq.29는 쉽게 통합된다. eq.32 조건을 만족시키는 해법은

$({displaystyle {cases}a^{2}=p_{1} \Lambda }{\operatorname {ch}(2 p_1} \Lambda \lambda )},\b^{2}e^{2\Lambda (p_{2} p_{1}) } ) } } }$

(eq.33)

여기서₀ b와₀ c는 두 개의 더 많은 상수입니다.

t → 0에서 함수 eq.33의 점근은 eq.30임을 쉽게 알 수 있다.이러한 함수와 θ → -dism에서의^{[note 8]} 함수 t(t)의 점근식은 다음과 같다.

$(\displaystyle a\sim e^{-\Lambda p_{1}\tau},\b\sim e^{\Lambda (p_{2}+2p_{1}\tau },\sim e^{1}\sim e^{1}\tau },\sim e_1B$

a, b, c를 t의 함수로 표현하면 다음과 같이 된다.

$(\displaystyle a\sim t^{p'_{l}, b\sim t^{p'_{m}, c\sim t^{p'_{n})$

(eq.34)

어디에

${\displaystyle p'_{l}=p_{1}{1-2 p_{1},p'_{m}=-{\frac {2 p_{1} -p_{2},p'_{n}=p_{1}p_{1},p'_{n} =p_{1} p_1}$

(eq.35)

그리고나서

$(\displaystyle abc=\Lambda't,\Lambda'=(1-2 p_{1})\Lambda.}$

(eq.36)

위의 그런 방식으로 교란 행위 다른 Kasner 모드를 갖추어야 하며, 이 과정에서 방향 나는 방향 m까지 t, 대칭의 부정적인 힘 Kasner 모드로 변신:기 전날pl<0이 지금은p고<0을 보여 준다.이 변화 동안에 그 기능 a(t)최대를 통해 b(t)최소를 통과한다;b, 이전 w. 통과감소에 따라 증가: 증가로부터의 a는 감소하며 감소하는 c(t)는 더 감소합니다.이전에는 증가하던 섭동 자체(eq.29의 δa^24α)가 이제는 감소하여 사라지기 시작한다.추가 진화는 마찬가지로 eq.26의 μ(θ² 대신) 항에서² 섭동의 증가를 야기하며, 카스너 모드의 다음 변경 등은 다음과 같다.

파라미터화 eq.5의 도움을 받아 전력 대체 규칙 eq.35를 작성하는 것이 편리합니다.

${\displaystyle {f}\mathrm {if} &p_{l}=p_{1}(u)=p_{2}(u)&p_{n}=p_{3}(u)\mathrm {then} &p'_{l}=p_{2}(u-1)&p_{u}{p}$

(eq.37)

두 가지 양의 힘 중 더 큰 힘은 여전히 양의 힘이다.

BKL은 이 음의 힘의 방향 전환은 카스너 시대라고 부릅니다.특이점 접근에 대한 미터법 진화의 특성을 이해하는 열쇠는 규칙 eq.37에 따라 p, p_m, p의_ln 거듭제곱을 사용한 정확히 이 카스너 시대 교대 과정이다.

방향 l과 m(Kasner epoch) 사이의 음의 검정력₁ p의 플립을 수반하는 연속적인 교대 eq.37은 u < 1의 순간까지 초기 u의 전체 부분의 고갈에 의해 계속된다.값 u < 1은 eq. 6에 따라 u > 1로 변환됩니다. 이때 음의 검정력은 p 또는_m p인_l 반면_n p는 두 개의 양수 중 작은 값이 됩니다(p_n2 = p).다음 일련의 Kasner Epoch는 방향 n과 l 사이 또는 방향 n과 m 사이에 음의 전력을 플립합니다.u의 임의의 (비합리적인) 초기값에서 이 변경 프로세스는 ^{[note 9]}무제한으로 계속됩니다.

아인슈타인 방정식의 정확한 해에서, p_m, p_n, p는_l 원래의 정확한 감각을 잃는다.이러한 상황으로 인해 이들 수치(및 파라미터 u)의 결정에 약간의 "불안함"이 발생하며, 이는 작지만 u의 확실한(예를 들어 합리적인) 값의 분석이 무의미해진다.따라서 u의 임의의 비합리적인 값에 관련된 이러한 법칙만이 특별한 의미를 가집니다.

세 번째 축을 따라 거리가 단조롭게 줄어드는 동안 두 축을 따라 공간 거리의 척도가 진동하는 더 큰 기간을 시대라고 합니다. 부피는 ~ t에 가까운 법칙에 따라 감소합니다.한 시대에서 다음 시대로 이행할 때 거리가 단조롭게 줄어드는 방향은 한 축에서 다른 축으로 플립됩니다.이러한 전환 순서는 랜덤 프로세스의 점근 특성을 획득합니다.같은 랜덤 순서는 연속된 연대의 길이 교대에도 특징입니다(연대에 따라 BKL은 시간 간격이 아니라 한 연대가 포함하는 카스너 에폭의 수를 파악합니다).

각 시대(s번째 시대)는 최대 $s)$ {displaystyle $u_$${\$$max}^{(s$부터 시작하여 $s)$ {{\$max}^{(s)}}$까지 파라미터 $u$의 일련의 값을 지원합니다.${\displaystyle {}_{(}^{}}$ ${\displaystyle s_{}^{}}$) { $displaystyle$u _ { \$min }^{$ ( s$$) }}$$ < 1 。그리고나서

${\displaystyle u_{\min }^{(s)}=x^{(s)},\u_{\max }^{(s)}=k^{(s)}+x^{(s)}},$

(eq.41)

즉^(s), k = [ ${\displaystyle u_{}^{}}$max (${\displaystyle s_{}^{}}$) \ $displaystyle$u _ { \ $max }^{$ ($s$ )$$]입니다.여기서 괄호는 값의 전체를 의미합니다.숫자^(s) k는 연대의 길이로, 해당 연대가 포함하는 카스너 에폭의 수로 측정됩니다.다음 시대를 위해

${\displaystyle u_{\max }^{(s+1)}=param frac {1}{x^{(s)}}},\k^{(s+1)}=\left[{\frac {1}{x^{(s}}}}\right]}$

(eq.42)

이러한 규칙에 의해 구성되는 무한 연속수 u에는 무한히 작은 값^(s) x와 그에 상응하는 무한히 큰 길이^(s) k가 있습니다.

시계열은 t = 0에 가까워질수록 밀도가 높아집니다.그러나 이 진화의 시간 경로를 기술하는 자연 변수는 세계 시간 t가 아니라 특이점에 도달하는 전체 과정이 -θ까지 확장되는 로그 ln t이다.

eq.33에 따르면, 카스너 에폭 사이의 전환 중 최대치를 통과하는 함수 a, b, c 중 하나는 최대치의 피크에서 다음과 같다.

${\displaystyle a_{\max}=sqrt {2\Lambda p_{1}(u) }}$

(예.38)

여기서 a는 b와₀ c에 비해₀ 크다고 가정한다_max. eq 38 u는 전이 전 카스너 시대의 매개변수 값이다.여기서 보면 시대별 연속 최대치 피크가 점차 낮아지고 있음을 알 수 있다.실제로 다음 카스너 시대에는 이 매개변수가 u' = u - 1을 가지며, eq.36에 따라 δ' = δ(1 - 2₁ p(u))로 대체된다.따라서 2개의 연속 최대값의 비율은

${\displaystyle {a'_{\max }}{a_{\max }=\left[{\frac {p_{1}(u-1)}}{p_{1}(u)}}\left(1-2 p_{1}(u)\right)\right]^{\frac {2}}}$

그리고 마지막으로

${\displaystyle {a'_{\max}}{a_{\max}={frac {u-1}{u}}}\equiv {\frac {u}}}.}$

(eq.39)

위는 진공 상태의 아인슈타인 방정식에 대한 해이다.순수 카스너 모드에 대해서는 물질이 이 용액의 질적 특성을 바꾸지 않고 필드에서의 반응을 무시한 상태로 쓸 수 있다.그러나 아인슈타인 방정식의 정확한 해법으로 이해되는 논의 중인 모델에 대해 이것을 한다면, 물질 진화의 결과적인 그림은 일반적인 특징을 가지지 않을 것이고 현재 모델에 임박한 높은 대칭성에 대해 구체적일 것이다.수학적으로, 이 특수성은 여기에서 논의된 균질 공간 기하학의 경우, Ricci 텐서 $성분{\displaystyle {}_{}^{}}$ ${\displaystyle R_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$0 ({\$displaystyle R_${\alpha }^$0$$})$은 동일하게 0이며, 따라서 아인슈타인 방정식은 물질의 이동을 허용하지 않는다는 사실과 관련이 있다.${\displaystyle T_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$0 (\$displaystyle T_{\alpha$}^{$0})$즉, 동기 프레임은 물질에 관해서도 함께 움직여야 합니다.eq. 19_α u = 0⁰, u = 1로 치환하면 θ ~ (θ)^−4/3 ~ t가^−4/3 된다.

제한(t → 0에서) 메트릭의 주요 항만 모델에 포함시키고 밀도와 속도의 임의의 초기 분포가 있는 문제를 모델에 기록하면 이러한 어려움을 피할 수 있다.그 후 물질의 진화의 과정은 규칙 21이 되는 운동의 일반 법칙 17과 규칙 18에 의해 결정된다.카스너 시대마다 밀도는 법칙에 따라 증가한다.

$\displaystyle \varepsilon = t^{-2(1-p_{3})},$

(예 40)

여기서₃ p는 위와 같이 p, p₂, p₃ 중 가장 큰 숫자이다₁. 물질 밀도는 특이점을 향해 진화하는 동안 단조롭게 증가한다.

메트릭의 진화

매우 큰 u 값은 카스너 파워에 해당합니다.

${\displaystyle p_{1}\apprough - {\frac {1}{u}, \p_{2}\apprough p_{3}\apprough 1-{\frac {1}{u^{2}},$

(eq.43)

값(0, 0, 1)에 가깝습니다.0에 가까운 두 값도 서로 가깝기 때문에 세 가지 유형의 "퍼터베이션"(eq.26 오른쪽에 μ, θ가 있는 용어) 중 두 가지 유형의 변화도 매우 유사하다.이러한 긴 시대가 시작될 때 두 카스너 시대 사이의 전환 순간에 이러한 용어들이 절대치에 매우 가깝다면(또는 초기 조건을 할당하여 인위적으로 만들어짐) 전체 시대의 대부분 기간 동안 근접하게 유지될 것이다.이 경우(BKL은 이를 작은 발진의 경우라고 부른다), 한 유형의 섭동의 작용에 기초한 분석은 부정확해진다; 두 가지 섭동 유형의 동시 효과를 고려해야 한다.

두 가지 섭동

a, b, c(a와 b로 해두면 된다)의 2개의 함수가 작은 진동을 일으키지만, 3번째 함수(c)는 단조롭게 감소하는 긴 시대를 생각해 보자.후자의 함수는 빠르게 작아집니다. a와 b에 비해 c를 무시할 수 있는 영역에서만 솔루션을 생각해 보십시오.먼저 타입 IX 공간 모델에 대해 = μ = μ = ^[43]= 1로 치환하여 계산한다.

함수 c를 무시한 후, 첫 번째 2개의 방정식 eq. 26은 다음을 나타낸다.

$\displaystyle \alpha _{\display \displays \displays }+\displays \displays \displays \displays }= 0,$

(eq.44)

${\displaystyle \alpha }-\displays \alpha }=e^{4\displays }-e^{4\alpha },$

(eq.45)

그리고 eq.28은 다음 형식을 취하는 세 번째 방정식으로 사용될 수 있다.

$\displaystyle \flash \flash }\left(\alpha _{\flash \flash }+{\flac {1}{4}\left(e^2\flac }-e^2\flac })^{\fright} } =-\flash {\flash } } } } {\flash } } } } } 。$

(eq.46)

eq.44의 해답은 다음 형식으로 작성된다.

$\displaystyle \alpha +\ln a_{0}^{2}}{\xi _{0}}\left(\display -\ln _{0}\right)+2\ln a_{0}.$

여기서₀ α, θ는₀ 양의 상수이고 θ는₀ 변수 θ에 대한 시대의 상한이다.( ( 대신) 새로운 변수를 추가 도입하는 것이 편리합니다.

$\displaystyle \xi = \xi _ {0} \exp \left [ { \ frac { 2a _ { 0 } { \ xi _ { 0 } } \ left ( \ flac - \ right ) ]}$

(eq.47)

그리고나서

${\displaystyle \alpha +\ln =\ln {frac {xi } {\xi _{0} +2\ln a_{0}.}$

(eq.48)

변수 θ = α - β를 도입하여 방정식 eq.45와 eq.46을 변환한다.

${\displaystyle \chi _{\xi \xi } = frac {\xi }} + {\frac {1}{2}} \operatorname {sh} 2 \chi = 0,}$

(eq.49)

$\displaystyle _{\xi }=-{\frac {1}{4}}\xi +{\frac {1}{8}}\xi \left(2\chi _{\xi }^{2}+\operatorname {ch} 2\chi -1\right).}$

(예. 50)

to에서₀ - cor로 from의 감소는 to에서₀ 0으로 from여기서 고려되는 근접 a와 b의 긴 시대(즉, ),가 작은 시대)는 is가₀ 매우 많은 경우에 구한다.실제로, 일반적으로 1/θ에 의한 첫 번째 근사치에서의 eq.49의 해는 다음과 같다.

$\displaystyle \chi =\alpha -\displays = harcfrac {2A}{\sqrt {xi }}\sin \left(\xi -\xi _{0}\right)}$

(eq.51)

여기서 A는 상수이고 $승수{\displaystyle \frac{\mathrm{}}{}}$ 1 ${\({$}}})은$$ a을 소량으로 만들기 때문에 eq.49에서 sh 2 ≈ 2 ${\displaystyle \frac{\sqrt{sh}}{}}$ 2 ^{[note 10]}sh로 대체할 수 있습니다.

eq.50부터 취득한다.

${\displaystyle _{\xi } = flac {1}{4}} \xi \left (2\chi _{\xi }^2} +\chi ^{2}\right) =A^{2},\mathrm = A^{2}\left(\xi -\xi _{0}\right)+\mathrm {const}.}$

eq.48과 eq.51에서 α와 β를 구하고 위의 근사치에 따라 e와^β e를 직렬로 확장한^α 후 최종적으로 ^{[note 11]}다음을 얻는다.

${\displaystyle {case}a\b\end{case}=a_{0}}{\displayrt {frac}{\xi_{0}}}\left[1\pm {frac {A}{\sqrt {xi}}\sin 왼쪽(\xi -\xi _0}\right)\right)$

(eq.52)

$(\displaystyle c=c_{0}e^{-A^{2}\left(\xi _{0}-\xi \right)}).}$

(예.53)

변수 θ와 시간 t 사이의 관계는 다음과 같은 정의 dt = abc dθ의 적분에 의해 얻어진다.

$(\displaystyle {t} {t_{0}}=e^{-A^{2}\left(\xi _{0}-\xi \right)}).}$

(예 54)

상수₀ c(θ = θ에서₀ θ의 값)는 이제₀ c$$θ {$displaystyle \ll }$α가$$₀ 되어야 합니다.

이제 도메인$ξ1$에 대해 설명하겠습니다$.$다음은 eq.49의 솔루션의 주요 용어이다.

$\displaystyle \chi =\alpha -\display =k\ln \xi +\mathrm {const} ,,}$

where k is a constant in the range − 1 < k < 1; this condition ensures that the last term in eq. 49 is small (sh 2χ contains ξ^2k and ξ^−2k).그리고 α, β, t를 결정하면 다음과 같이 된다.

${\displaystyle a\sim ^{1+k}{2},\b\sim \xi ^{\frac {1-k}{2},\c\sim \xi ^{-{\frac {1-k^{2}}{4},\sim \xi ^{\frac {3+k^2}}{4}}}}.}$

(eq.55)

이것은 다시 함수 c(^{[note 12]}t)에 음의 t전력이 존재하는 Kasner 모드입니다.

이러한 결과는 위에서 설명한 것과 질적으로 유사한 진화를 그리고 있습니다.큰 감소 µ 값에 해당하는 장기간에 걸쳐 두 기능 a와 ${\displaystyle \frac{}{}}$는 a${\displaystyle }$- b ~${\displaystyle 1\frac{\mathrm{}}{}}$ $†$에 근접하여 진동합니다.\$sim${ $tfrac {1}$ \$sqrt {xi$$$}$。$동시에, ${\displaystyle \frac{a}{}}$와 b는$$모두 천천히 기능합니다$(\sim$감소하다.진동 주기는 변수 δ : δ = 2µ(또는 로그 시간별 주기 δ ln t = 2µα²)로 일정합니다.세 번째 함수 c는 c = ct₀/t에₀ 가까운 법칙에 의해 단조롭게 감소한다.

이 진화는 § 1까지 계속되며 공식 eq. 52와 eq. 53은 더 이상 적용되지 않는다.그 지속시간은 t가 t에서₀ 값₁ t로 바뀌는 것에 대응하며, 이는 다음과 같이 θ에₀ 관련된다.

${\displaystyle A^{2}\xi _{0}=\ln {frac {t_{0}}{t_{1}}.}$

(eq.56)

이 시간 동안의 and과 t의 관계는 다음과 같이 나타낼 수 있다.

${\displaystyle {\frac {\xi} {\xi _ {0} = frac { t_{1}} {\ln {tfrac {t_{0}} {t_{1}}}}.}$

(eq.57)

그 후 eq.55에서 보듯이 감소함수 c는 증가하기 시작하고 함수 a, b는 감소하기 시작한다.이 Kasner 시대는 eq 22의² c/ab²² 항이² ~ t가 되고 다음 일련의 진동이 시작될 때까지 계속됩니다.

논의 중인 장기간의 밀도 변화에 대한 법칙은 eq. 20의 eq. 52를 대체함으로써 얻을 수 있다.

$(\displaystyle\varepsilon\sim\leftfrac\xi_{0}}{\xi}}{2})$

(eq.58)

changes가 to에서₀ 11로 바뀌면 밀도가 $(\$배$$ 증가)한다.

함수 c(t)가 c ~ t에 가까운 법칙에 의해 변화하지만, 메트릭 eq.52는 검정력(0, 0, 1)을 갖는 카스너 메트릭에 해당하지 않는다는 점을 강조해야 한다.후자는 eq-27에 의해 허용되는 Taub에 의해^[47] 발견된 정확한 해와 일치한다.

${\displaystyle a^{2}=bcfrac {p}{2}}{\frac {ch}(2p\flac +\flac _{1}}{\mathrm {ch}(p\flac +\flac _{2}}}}},\c^{2}=blac {p}{p} {p} {p}$

(eq.59)

여기서 p, ,, are는₁₂ 상수입니다.점근영역 θ → -t에서 치환 = t 후^рτ a = b = const, c = const.t를 얻을 수 있다.이 메트릭에서 t = 0에서의 특이성은 비물리적이다.

이제 eq. eqs. 26'–'28 µ = -1, μ = µ = 1로 대체하여 타입 ^[44]VII 모델의 유사한 연구를 설명하자.

장기간에 걸쳐 단조감소함수가 a일 경우, 전술한 해석에서는 아무것도 변하지 않는다.식 26, 28의 오른쪽에 있는 a를 무시하면², 같은 식 49, 50으로 돌아간다(표기 변경).단, 단조롭게 감소하는 함수가 b 또는 c일 경우에는 c로 합니다.

이전과 같이 a(θ)와 b(θ)의 기호가 같은 방정식 49를 가지며, 따라서 a(θ)와 b(θ)의 전자의 식 eq. 52를 가지지만 방정식 50은 다음과 같이 치환된다.

$\displaystyle _{\xi }=-{\frac {1}{4}}\xi +{\frac {1}{8}}\xi \left(2\chi _{\xi }^{2}+\mathrm {ch} 2\chi +1\right).}$

(예 60)

현재 now의 주요 용어는 다음과 같다.

$(\displaystyle _{\xi }\약 {frac {1}{8}\xi \cdot 2,\display \frac {1}{8}\left(\xi ^{2}-\xi _{0}^2}\오른쪽))$

하도록

${\displaystyle {\frac {c}{c_{0}}=e^{-{\frac {1}{8}}\left(\xi_{0}^{2}-\xi^{2}\right)}.}$

(eq.61)

시간 t의 함수로서 c의 값은 다시 c = ct₀/t이지만₀, θ의 시간 의존성은 변한다.긴 연대는 according에₀ 따라 달라진다.

$(\displaystyle \xi _{0}=syslogrt {8\ln {frac {t}{t_{0}}})}$

(예.62)

한편, 이 값 θ는₀, 한 시대(θ₀/2al)에 있어서의 함수 a, b의 발진수를 결정한다.한 시대의 길이(즉, 주어진₀ 비율 t₁/t)가 주어진다면, 일반적으로 타입 VII의 진동 수는 타입 IX의 진동 수보다 적을 것이다.진동 주기의 경우 이제 δ in t = δt/2가 됩니다. 유형 IX와 달리 주기는 긴 시간 동안 일정하지 않고 δ와 함께 서서히 감소합니다.

스몰타임 도메인

긴 시대는 여러 시대에 걸친 시간 간격의 진화를 연구하는 것을 어렵게 만드는 "규칙적인" 진화 과정을 위반합니다.그러나 그러한 "비정상" 사례는 임의의 초기 조건을 가진 시작점으로부터 충분히 큰 거리에서 점근적으로 작은 시간 t의 단일점으로의 모델의 자발적 진화에 나타난다는 것을 보여줄 수 있다.긴 시대에도 카스너 시대 사이의 전환 동안 두 진동 함수는 매우 다르게 유지되어 하나의 섭동의 영향 아래에서 전환이 발생합니다.이 섹션의 모든 결과는 VII 및 ^[48]IX 유형에 동일하게 관련되어 있습니다.

각 카스너 에폭 abc = δt, 즉 α + β + δ = ln δ + ln t.한 에폭(파라미터 u의 주어진 값으로)에서 다음 에폭으로 전환할 때 상수 δ에 1 + 2p₁ = (1 – u² + u)/ (1 + u²) < 1을 곱하면 δ의 체계적인 감소가 발생합니다.그러나 한 시대 동안 ln Ω의 전체 변동의 평균 값(시대 길이 k에 대한)은 유한해야 한다.실제로 평균값의 분산은 k 증가에 따른 이 변동의 너무 빠른 증가에만 기인할 수 있다.파라미터 u의 큰 값의 경우 ln(1 + 2p₁) - -2/u입니다.k가 클 경우 최대값^(max) u = k + x µ k이다.따라서 한 시대 동안 ln Ω의 전체 변동은 형태의 합으로 주어진다.

$\displaystyle \sum \left(1+2p_{1}\오른쪽)=\frac +{\frac {1}{k-2}}+{\frac {1}+{\frac {1}{k}}}$

u의 큰 값에 해당하는 항만 적습니다.k가 증가하면 이 합계는 ln k만큼 증가합니다.단, eq.76에 따라 길이 k가 큰 시대가 출현할 확률은 1/k만큼₂ 감소하므로 상기 합계의 평균값은 유한하다.따라서 다수의 에라스에 걸친 ln δ량의 계통적인 변화는 이 숫자에 비례하게 된다.그러나 eq.85에서는 t → 0일 때 숫자 s가 단순히 ln t처럼 증가한다는 것을 알 수 있다.따라서 임의로 작은 t의 점근 한계에서는 ln t에 비해 ln δ라는 용어를 무시할 수 있다.이 근사치에서는

$\displaystyle \alpha +\displays +\displays =-\Omega ,,}$

(예.63)

여기서 δ는 "대수 시간"을 나타냅니다.

${\displaystyle \Omega =-\ln t.,}$

(예 64)

그리고 시대적 전환의 과정은 일련의 짧은 시간 섬광으로 볼 수 있다.진동 스케일 함수의 최대 크기에도 체계적인 변화가 있습니다.eq.39에서 u ${\displaystyle 11}$의 ${\displaystyle {경우}_{}}$ ${\displaystyle {최대}_{}^{}}$ ${\displaystyle -}$ - ${\displaystyle {}_{}}$/ ${\displaystyle 2}$u { $display style$ a _ { \ $max }^{$ \ prime } - a _ { \ $max$} \$- in$in $in{\displaystyle {}_{}^{}}$ in in in in in in in in in in in in in in in in in in in in in in in in in in in in {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ ras는 단순히 ln Ω으로 t → 0으로 증가합니다.최소값의 저하와 발진폭의 증가를 동시에 δ에 비례하여 진행한다(eq.77).입양된 근사는 최대치는 저음과 서신에는 진폭의 증가와 비교에 있는 모든 진동 기능의 최대 가치와 수량, β α에 그렇게 αmax=0,βmax=0으로, γmax)0에서는 무시된다, γ는 함께 시간의 각에 연결되어 있을 때 부정적인 값에 의해서만 운영된다. 관계.예.63.

이러한 에폭의 순간적인 변화를 고려하면, 에폭의 길이에 비해 이행 주기는 작은 것으로 무시되며, 실제로 이 조건은 ^{[note 14]}충족된다.α, β 및 δ maxima를 0으로 치환하려면 각 함수의 진동 진폭에 비해 ln(p₁ δ)이 작아야 한다.위에서 설명한 바와 같이, 에라스₁ 간 전환 중에는 p 값이 매우 작아질 수 있지만, 그 발생 규모와 발생 확률은 각 모멘트의 진동 진폭과 관련이 없습니다.따라서 원칙적으로 상기의 조건(최대치 제로)을 위반할 정도로 작은₁ p값에 도달할 수 있습니다.이처럼 α의_max 급격한 감소는 규칙 eq.37에 의해 카스너 시대 사이의 전환이 부정확해지는 다양한 특수한 상황을 초래할 수 있다(위에서 설명한 상황을 포함).이러한 "위험한" 상황은 아래의 통계 분석에 사용되는 법률을 위반할 수 있다.단, 전술한 바와 같이 이러한 편차에 대한 확률은 점근적으로 0으로 수렴됩니다.이 문제는 아래에서 설명합니다.

변수 u가 값을 통과하는 k Kasner epoch를 포함하는 시대를 고려합니다.

${\displaystyle u_{n}=k+x-1-n,\cdots,k-1,}$

(예 65)

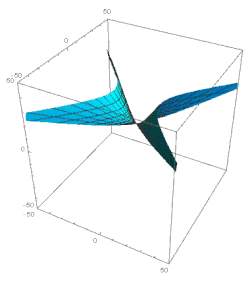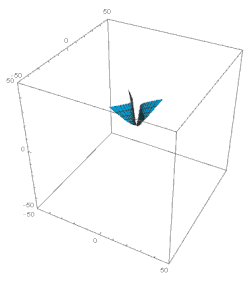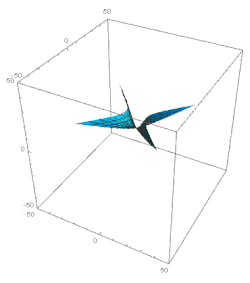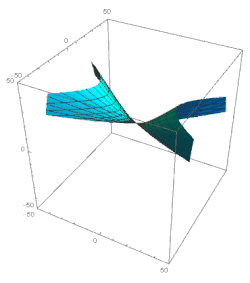
α와 β를 이 시대의 진동 함수라고 합니다(그림 4).^{[note 15]}

파라미터_n u가 있는 카스너 에폭의 초기 모멘트는 δ이다_n.각 초기 모멘트에서 값 α 또는 β 중 하나는 0이고 다른 하나는 최소값이다.연속 최소값의 α 또는 β 값, 즉 모멘트 δ는_n 다음과 같다.

${\displaystyle \alpha _{n}=-\display_{n}\Omega _{n},}$

(예.66)

(최소 α와 β를 구별하지 않음).각 Ω_n 단위로 이러한 최소값을 측정하는 값 θ는_n 0과 1 사이에서 실행할 수 있습니다.함수 δ는 이 기간 동안 단조롭게 감소한다; eq.63에 따르면 모멘트 δ의_n 값은

$\displaystyle _{n}=-\Omega _{n}(1-\displaystyle _{n}).\,}$

(eq.67)

모멘트_n δ에서 시작하여 모멘트_n+1 δ에서 끝나는 신기원 동안 함수 α 또는 β 중 하나는 선형 법칙에 따라 각각 - δ에서 0으로 증가하며 다른 하나는 0에서 - δ로 감소한다.

${\displaystyle \mathrm{c}}$ ${\displaystyle \mathrm{o}}$ ${\displaystyle \mathrm{n}}$ ${\displaystyle \mathrm{s}}$ t${\displaystyle }$+ ${\displaystyle p{}_{}{1\mathrm{}}_{}}$ (${\displaystyle {}_{}{u}_{}}$ n )$$ \ $displaystyle$\$mathrm { const$} + $p_{1}(u_{n})$ \ $Omega$}, 및$$ $c{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{o}}$ n s ${\displaystyle \mathrm{t}}$ -${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}{}_{}}$ ${\displaystyle n_{}}$ \ $displaystyle$\ $mathrm${ $const}$ - $p_{2}(u_{n})$$\Omega \,}$

재발 관계를 초래하다

${\displaystyle _{n+1}\Omega _{n+1}=black {1+u_{n}}{u_{n}}\black _{n}\{n}=black {1+u_{0}}}{u_{n}}\delta_{0}\Omega_{0}}$

(eq.68)

그리고 로그 에폭의 길이에 대해

${\displaystyle \Delta _{n+1}\equiv \Omega _{n}-\Omega _{n}=black {f(u_{n})}{u_{n}}\delta _{n}\Omega _{n}=deltafrac {f(u_{n}(1+u_{n-1})}{f(u_{n-1})u_{n}}}\Delta _{n}}$

(예.69)

여기서, 줄여서 f(u) = 1 + u² + u입니다.n에폭 길이의 합은 다음 공식에 의해 구해진다.

$\displaystyle \Omega _{n}-\Omega _{0}=\left[n(n-1)+{\frac {u_{n-1}}\right}\displaystyle _{0}\Omega _{0}.}$

(예. 70)

eq.68에서 알 수 있듯이_n+1 α > α_n, 즉 함수 α 및 β의 발진폭은 계수 θ가_n 작을 수 있지만 전체 기간에 걸쳐 증가한다는 것을 알 수 있다.시대의 시작에서 최소값이 깊으면 다음 최소값이 더 낮아지지 않는다. 즉, 카스너 시대 사이의 전환 모멘트의 잔류물α – β는 큰 상태로 유지된다.이 주장은 에폭 사이의 전이가 긴 기간 동안 공통 규칙 eq.37에 의해 결정되기 때문에 시대 길이 k에 의존하지 않는다.

주어진 시대에 함수 α 또는 β의 마지막 진동 진폭은 α₀ = α (k + x) / (1 + x) 관계에 의한_k−1 첫 번째 진동의 진폭과 관련이 있습니다.k에 비해 몇 단위만큼 작은 k에서도 x를 무시할 수 있으므로 α 및 β 발진폭의 증가가 시대 길이에 비례한다.함수 a^α = e 및 b^β = e의 경우, 이는 시대가 시작될 때 진동 진폭이 A이면₀ 이 시대가 끝날 때 진폭이 ${\displaystyle {A\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$/ (${\displaystyle 1_{}^{}}$ +${\displaystyle x_{}^{}}$) {{$k/(1+x$이 $된다는{\displaystyle {}_{}^{}}$ 것을 의미합니다.

카스너 에폭의 길이(대수 시간)도 주어진 시대 내에서 증가한다. 즉, eq.69에서 δ_n+1 > ^{[note 16]}δ로_n 계산하기가 쉽다.총 연대는

$\displaystyle \Omega _{0}^{\prime}-\Omega _{0}\equiv \Omega _{0}=k\left(k+x+{\frac {1}{x}}\right)\displaystyle _{0}\Omega _{0}\equiv _{0}$

(eq.71)

(x가 1/x인 용어는 길이가 작은 x; cf인 마지막 k번째 에폭에서 유래한다.그림 2)특정 시대의 k번째 시대가 끝나는 모멘트_n δ는 다음 시대 시작의 모멘트 ₀δ'와 같다.

뉴에이지의 제1캐스너 에폭에서는 함수 θ가 전 시대에 도달한 최소값 θ_k = - δ_k(1 - θ_k)에서 최초로 상승하는 것으로, 이 값은 새로운 일련의 진동에 대해 개시 진폭 ₀δ'₀의 역할을 한다.다음과 같은 정보를 쉽게 얻을 수 있습니다.

$\displaystyle _{0}^{\prime}\Omega _{0}^{\prime}=\left(\display_{0}^{-1}+k^{2}+kx-1\right)\display_{0}\Omega _{0}.}$

(eq.72)

>₀₀ > >₀₀ > > > > > > > > > > > > > > >>그다지 크지 않은 k에서도 진폭 증가는 매우 중요합니다. 함수 c = e는^γ $진폭{\displaystyle {}_{}^{}}$ ${\displaystyle {A\mathrm{}}_{}^{}}$ 0${\displaystyle }$µ ~ ${\displaystyle {A\mathrm{}}_{}^{}}$ ${\displaystyle {{}^{}}_{}^{}}$ ${\displaystyle {{k\mathrm{}}^{}}_{}^{}}$ 2 ${\$ A_${k^{2$에서 진동을 시작합니다.상기의 「위험한」발진 상한의 대폭적인 저하의 문제에 대해서는, 현시점에서는 보류하고 있습니다.

eq.40에 따르면 첫 번째 (k - 1)세기 동안의 물질 밀도 증가는 다음 공식에 의해 나타납니다.

$\displaystyle \ln \frac \varepsilon _{n+1} {\varepsilon _{n}\right}=2\left[1-p_{3}(u_{n}\right]\델타 _{n+1}.$

주어진 시대의 마지막 k에 대해 u = x < 1에서 최대 전력은 p₂(x)입니다(p(x)가 아닙니다₃).따라서 전체 시대에 걸쳐 밀도 증가를 위해 얻을 수 있다.

$\displaystyle \ln \leftflon _{k}{\varepsilon _{0}}\equiv \ln \leftflac \frac \{0}{\right}=2(k-1+x)\mega _0}.}$

(예.73)

매우 좋지 않k값에도 그러므로, ε 0′/ε 0번 국도 A02k{\displaystyle \varepsilon_{0}'/\varepsilon _{0}\sim A_{0}^{2k}}. 다음 시대( 가진 길이 k')밀도 동안 빠르게 증가된 시작하는 진폭 0'으로:ε 0″/ε 0때문에 높아질 것이다′번 국도 A0′ 2k″번 국도 A02k2k. $§$ ${\displaystyle$ \$varepsilon _{$0}'/\$varepsilon _{0$}'^{$2k'}\$sim$A_{0}^2k^{2$}k$\text{'}\}$ $등$이러한 공식은 물질 밀도의 급격한 증가를 보여준다.

특이점 근처의 통계 분석

여기에 포함된^(s) 카스너 에폭의 수로 측정되는 연장 k의 시퀀스는 점근적으로 랜덤 프로세스의 특성을 획득합니다.한 시대에 걸쳐 다음 시대에 걸쳐 있는 발진 함수 쌍의 교환 순서도 마찬가지입니다(숫자^(s) k가 짝수인지 홀수인지에 따라 다름).이 확률성의 원천은 하나의 시대에서 다음 시대로의 전환이 u 값의 무한 수치 시퀀스로 결정되는 규칙 eqs.42이다.즉, 무한 시퀀스 전체가 특정 $초기값{\displaystyle {}_{}^{}}$ ${\displaystyle u_{}^{}}$max (${\displaystyle {0)}_{}^{}}$ $=$ (${\displaystyle 0^{}}$ +${\displaystyle {}^{}}$ ($)$ {$displaystyle u_{\max$}^{(0)}=$k^{(0)}+x^{(0$로 시작하는 경우, 연속된⁽⁰⁾ 분수의 팽창에 있는 k, k, ...의⁽¹⁾ 길이입니다.

${\displaystyle k^{(0)}+x^{(0)}=k^{(0)}+{\frac {1}{k^{(1)}+{\frac {1}{k^{(2)}+\frac }}}}}}.}$

(예 73a)

이 확장은 Tx = {1/x}, 즉 x_s+1 = {1/x_s} 공식에 의한 간격 [0, 1]의 매핑 변환에 해당합니다.이 변환은 구간 [0, 1]의 확장 변환, 즉 fθ(x) > 1인 변환 x → f(x)에 속합니다. 이러한 변환은 지수적 불안정성의 특성을 가지고 있습니다. 초기에 두 개의 근접점을 취하면 변환의 반복에 따라 상호 거리가 기하급수적으로 증가합니다.지수 불안정성이 강한 확률적 성질의 출현으로 이어진다는 것은 잘 알려져 있다.

일정한 초기값 x가 아니라⁽⁰⁾ 특정 확률론적 분포법 w(x)에₀ 따라 0에서 1 사이의 간격으로 분포된 값⁽⁰⁾ x = x를 고려함으로써 그러한 시퀀스의 확률론적 설명으로 전환할 수 있다.각 시대를 끝내는 x 값도^(s) 특정 법칙 w_s(x)를 따르는 분포를 가집니다.w(x)dx가 지정된 간격 dx에서 s번째 시대가 ${\displaystyle u_{}^{}}$max (${\displaystyle s_{}^{}}$ ) $=$ {\$displaystyle u_{\max }^{(s$)}=$x}$ $값$으로 끝날 확률이라고 가정합니다_s.

s번째 시대를 종료하는 값 x^(s) = x는 초기 $값{\displaystyle {}_{}^{}}$ ${\displaystyle u_{}^{}}$max ( ${\displaystyle s_{}^{}}$) ${\displaystyle {}_{}^{}x}$ +$$ { displaystyle $u_{\max }^{(s$)}=$x+k}$에서$$발생할 수 있습니다. 여기서 k = 1, 2, ...; ${\displaystyle {\mathrm{이러한}}_{}^{}}$u max${\displaystyle {}_{}^{}}$( $s$) { $style$u _ { \ $max$}^{$$( s )}의 $값$은 이전 시대의 값^(s–1) x = 1/(k + x)에 해당합니다$$.이 점에 유의하여 다음과 같은 반복 관계를 작성할 수 있으며, 이는 확률_s w(x)의 분포를 분포_s–1 w(x)로 나타낸다.

$_ {1}{k+xrighty}{\displaystyle w_{s}{x}_k={\sum}_{\sm}_in}$

★★★★★★★★★★★★★★★★★」

${{s}(x)=\sum _{k=1}^{\infty}{\frac {1}{\left(k+x\right)}w_{s-1}\left\frac {1}{k+x}\right}.}$

(예: 73c)

분포_s w(x)가 s를 증가시켜 분포 w(x)를 제한하는 정상(s와 독립)으로 향하는 경향이 있는 경우, 후자는 함수_s−1 w(x)와_s w(x)의 지수를 떨어뜨림으로써 eq. 73c에서 얻은 방정식을 만족시켜야 한다.이 방정식에는 해답이 있다.

$wdisplaystyle w(x)=flac {1}{\left(1+x\right)\ln2}}$

(eq.74)

(단일화로 정규화되어 ^{[note 17]}x의 첫 번째 순서로 이동).

s번째 시대의 길이 k를 가지려면 앞의 시대가 1/(k + 1)와 1/k 사이의 간격에서 숫자 x로 끝나야 합니다.따라서, 시대의 길이 k가 될 확률은 (정지 한계에서)와 같습니다.

$({displaystyle W(k)=\int \int _{1/(k+1)}^{1/k}w(x), param=param frac {1}{\ln2}}\ln {frac {(k+1)^2}}{k+2)}}}}.}$

(eq.75)

k의 큰 값에서

$(\displaystyle W(k)\display {frac {1}{k^{2}\ln 2)).}$

(예.76)

변환 x_s+1 = {1/x_s}의 에르고딕 특성과 우주론 모델의 통계적 특성을 관련짓는 데 중요한 점을 언급해야 한다.이 규칙에 따라 구성된 무한수열 x에서는 임의의 큰 길이 k에 대응하는 임의의 작은(그러나 소실되지 않는) x 값이 관찰된다.규칙 eq.37에 따라 서로 교환하는 카스너 시대의 시퀀스와 같은 시대의 개념이 의미를 상실할 때 그러한 경우(모델의 진동 진화의 모드가 여전히 지속됨에도 불구하고) 특정 상황을 야기할 수 있다.예를 들어, 카스너 시대의 "정기적인" 교환에서와 같이 eq26의 오른쪽에는 함수 a, b, c(a, a)뿐만⁴ 아니라 동시에 두 개의 함수(a⁴⁴, b²², ab)를 보유할 필요가 있음을 알 수 있다.

"불규칙적인" 일련의 진동에서 벗어나면 일련의 규칙적인 시대가 복원됩니다.변환 eq.42의 규칙적인 반복에 전적으로 기반을 둔 모델의 거동에 대한 통계적 분석은 중요한 정리에 의해 입증된다. 즉, 이 섹션의 마지막에 증명된 반복 횟수 s → θ(즉, 시간 t → 0)에 따라 비정상적인 사례의 출현 확률은 점근적으로 0이 되는 경향이 있다.이 주장의 타당성은 주로 모든 시대, 특히 한 시대에 다음 시대로의 전환에서 매우 빠른 진동 진폭 증가율에 기인합니다.

그러나 연속적인 e 동안 모델의 물리적 특성 변동에 대한 구체적인 법칙을 고려하여 (t → 0이 주어진 "초기 순간"에서 시작하는) "정지" 통계적 상태에 대한 우주론적 모델의 완화 과정은 이 상황 자체의 속성보다 덜 흥미롭다.악당

고정 분포가 설정되는 비율에 대한 개념은 다음 예에서 얻을 수 있습니다.초기값⁽⁰⁾ x를 일정한 숫자에 대해 폭θx의⁽⁰⁾ 좁은 간격으로 분포시키자.반복 관계 eq. 73c(또는 확장 eq. 73a에서 직접)로부터 분포_s w(x)의 폭은 다음과 같다고 쉽게 결론을 내릴 수 있다.

$x x kdisplaystyle x^{(0)}\cdot k^{(2)}{\displaystyle x^{(1) k^{(2)}$

(예: 76a)

(이 식은 수량 'x^(s)'를 1로 정의하고 있는 경우에만 유효합니다).

이 분포에서 계산한 $평균값{\displaystyle \stackrel{}{}}$ k ${\$ ${\displaystyle$ {$k$는 대수적으로 분산됩니다.매우 크지만 여전히 유한한 수 N의 경우 k ${\displaystyle ~}$ ~${\displaystyle \mathrm{in}n}$N(\$displaystyle {k}\sim \ln$ N$)$을 $가집니다{\displaystyle \stackrel{}{}}$.이 경우 평균의 유용성은 매우 제한됩니다.W(k)의 감소가 느리고 k의 분산이 평균보다 빠르기 때문입니다.이 수열의 보다 적절한 특성은 이 수열에서 랜덤으로 선택된 숫자가 K가 큰 길이인 K의 시대에 속할 확률입니다.이 확률은 lnK / lnN입니다.$1{\displaystyle \mathrm{}k}$ K${\displaystyle n}$N \ $displaystyle$ 1 \ $ll$K \ $ll$ N$.$ 1 。이 점에서 랜덤으로 선택된 숫자는 높은 확률로 장대에 속한다고 할 수 있습니다.

k와^(s)(s) x에 동시에^(s) 의존하는 식을 평균화하는 것이 편리하다. 이 두 수량은 모두 (이전 시대를 끝낸) 동일한^(s–1) 양 x에서 도출되기 때문에 공식^(s) k + x = 1^(s–1)/x에 따라 이들의 통계 분포는 독립적이라고 볼 수 없다.두 수량의 결합 분포_s W(k,x)dx는 후자의 치환 x → 1/(x + k)로 함으로써 분포_s–1 w(x)dx에서 구할 수 있다.즉, 함수_s W(k,x)는 eq.73c 오른쪽의 합계 부호 아래에 있는 식에 의해 주어진다.정상 한계에서는 eq.74에서 w를 취하면 다음과 같이 된다.

${\displaystyle W(k,x)=frac {k+x+1}{\left(k+x\right)\ln 2}.}$

(예: 76b)

k에 대한 이 분포의 합계는 eq.74로 돌아오고 dx에서 eq.75까지의 적분으로 돌아간다.

시대 간 전이를 정의하는 반복 공식은 초기(s = 0)로 정의된 일부 시대부터 시작하여 연속 시대(특정 시대의 카스너 시대가 아님!)에 번호를 매기는 지수 s로 다시 작성된다.δ^(s)(s) 및 δ는 각각 s번째 시대의 초기 모멘트 및 초기 물질 밀도이고, δ는 주어진^(s) 시대에 진동하는 함수 쌍α, β, δ의 초기 발진 진폭이며, k는 s번째 시대의^(s) 길이이고, x는 k=1에^(s) 따라 다음 시대의^(s+1) 길이(가스너 에폭의 수)를 구한다.eq에 따르면 71-73

$^{(^{( {1Display}\style}\display$

(eq.77)

$1)}x^{(^{(display$

(eq.78)

$^{(s+1right(k \ln}\flac{s}\stylevelon ^{s}\flan ^{s}\styleft}\flan}\flan}\flan ^{(s})\flan}\fl$

(eq.79)

(추가로^(s) 사용하기 위해 eq. 77에 도입되었다.)

수량 θ는^(s) 안정적인 정상 통계 분포 P(θ)와 안정적인(상대적인 변동이 작은) 평균값을 가진다.그들의 결정을 위해 BKL[48](때문에 조건부로) 대략적인 메서드는 임의의 양 δ(s)의 통계적 독립성과 무작위 수량, x(s)k(s)의 가정에 입각하곤 했다.그 기능은 6.2.1P(δ)적분 방정식은 사실은 양 δ(s)관계 eq로 상호 연결되어 있δ(s+1)를 표명했다. 78이 설립되었다.분포: 이 방정식은 수치적으로 해결되었습니다.이후 연구에서 Khalatnikov ^[49]등은 분포 P(θ)가 실제로 분석 방법에 의해 정확히 발견될 수 있음을 보여주었다.

정상 한계 내의 통계적 특성에 대해서는 변환 Tx = {1/x}을(를) 음의 지수로 제한 없이 계속함으로써 이른바 자연 확장을 도입하는 것이 타당하다.그 숫자들(x0, x1, 미국,...)의 일방적인 무한한 순서, equalities Tx){1/x}으로 연결되어,에서"두배로 무한한"시퀀스 X 그렇지 않으면 언급된 것처럼, 이것은 전환)동일한 equalities에 의한 모든–∞<>에 연결되어 있는 숫자의(..., x−1, x0, x1, 미국,...)의<>∞.물론, 그러한 팽창기 위해서는 그대로의 뜻 것은 아니다단어(x는 x에 의해_s 고유하게 결정되지 않기 때문에_s–1) 그러나 확장 시퀀스의 모든 통계 특성은 전체 길이에 걸쳐 균일하다. 즉, 임의 이동과 관련하여 불변하다(그리고₀ x는 "초기" 조건의 의미를 잃는다).시퀀스 X는 규칙_s k = [1/x_s–1]로 구성된 정수 K = (... k₋₁, k₀, k₁, k₂, k, ...)의 시퀀스와 동일합니다.반대로, 모든 X의 수는 무한 연속 분수로 K의 정수에 의해 결정된다.

$displaystyle x_{s}=black {1}{k_{s+1}+{\flac}{\flac}{\flac}{1}{{\flac}}$

(eq.79a)

(x${\displaystyle s_{}^{}}$ +${\displaystyle {}_1^{}}$+ {\$displaystyle x_{s+1}^{+}}$ $표기법$을 도입하는 편리성은 다음과 같습니다).간결한 표기법에서는 연속분수는 단순히 분모의 열거(대괄호 안)로 표시됩니다.그러면 ${\displaystyle x_{}^{}}$s$$+ {\$displaystyle x_{s}^{+}$의 $정의$는 다음과 같이 쓸 수 있습니다.

$s},displaystyle \ {\displaystyle x_{s}[k_{s+1},\display \right}$

(eq.79b)

방향)을 갖는 된다. 분모는 분모(분모)이다.

$displaystyle \right]{\displaystyle x_{s}[k_{display \right]}$

(eq.79c)

그 복귀 관계 eq.78이 일시적으로 표기법 ηs)(1− δs)/δs을 소개하는 것으로 변한다.그리고 eq.78로 다시 쓸 수 있어

$\1} _svsdisplaystyle \eta_{s+1}=svfrac{1}{\eta_{s}x_{s-1}+k_{s}s$

.

$_ [displaystyle \displaystyle \eta_{s+1}[k_{s-1},\displaystyle \right \}x_{s+1}^{-1}}$

따라서))s−/)의+{\displaystyle \eta_{s}=x_{s}^{-}{s}^{+}}그리고 마침내 sη.

${\= + {\ displaystyle \ displaystyle \ frac {x_{s}^{+}} {x_{-}}}} {\ displaystyle \ flac {x_{s} {x_{s}^{+{s}}}}}} {x_{-}}}}}$

(eq.79d)

δs에 이 표현 법은 각각의 간격[0,1]에서 값을 가정한다만 두(3[48]에 있는)임의의 양)의+{\displaystyle x_{s}^{+}}과 sx({\displaystyle x_{s}^{-}}을 포함하고 있다.

79c 1/xs−=-1s−+k의 x s −+[1/)의+]{\displaystyle 1/x_{s}[1/x_{s}^{+}\right]}. 따라서 시퀀스 전체 X의 한 걸음에 따라 올바른 역할로의 변화)의 수량이 합동 변환을 의미하+{\d 그것은 정의 eq에서 다음과 같이.isplaystyle $x_{s}^{+}$ $및$ x-s-{displaystyle x_{s}^{-}에 따라 $지정$합니다.

$frac frac 1}{ style x_1}^{+}}{-}}}{\display style x_{x_1+}^{{x}}}}}{x}}}{black}}{{{{black}}}}}}}}}}}{black}}}}}}}}}}}$

(예: 79e)

이것은 유닛 스퀘어에서의 일대일 매핑입니다.따라서 이제 한 수량의 일대일 변환 Tx = {1/x}이(가) 아닌 두 수량의 일대일 변환이 이루어집니다.

$수량{\displaystyle {}_{}^{}}$ ${\displaystyle x_{}^{}}$ s$$+ {\$displaystyle x_{$s}^{+} 및$$ ${\displaystyle x_{}^{}}$-$${\$displaystyle x_{s}^{-}$은 합동 고정 분포 P(x⁺, x⁻)를 가진다.eq.79e는 일대일 변환이므로 분포가 정지하는 조건은 함수 방정식으로 간단히 표현된다.

$Ptxdisplaystyle P\left(x_{s}^{+},x_displaystyle P\left(x_{s}^{-}\right)P\left(x_{s+1}^{+},x_{s+1}^{-}\)J}$

(예: 79f)

여기서 J는 변환의 야코비안입니다.

시퀀스 X의 1단계 시프트는 단위 제곱의 다음과 같은 변환 T를 발생시킨다.

$x1}{\prime}}= {displaystyle xprime}=blac {1}{x},\prime y^{\prime}{x} {\frac} {\frac} {x}$

($x$ ${\displaystyle {x\mathrm{}}_{}^{}}$0$$+ {\$display$x\$equiv$ x_${0$ $y{\displaystyle {}_{}^{}}$ ${\displaystyle {x\mathrm{}}_{}^{}}$0 -$${\$display style$ y$\equiv x_{0}^$_$\{-\},$ cf. eq. 79e).밀도 P(x, y)는 이 변환에 대한 불변 측도를 정의합니다.P(x, y)가 x와 y의 대칭 함수라고 가정하는 것은 당연합니다.즉, 측정치는 변환 S(x, y) = (y, x)와 관련하여 불변하므로 ST(x, y) = (xbs, y)의 곱 ST와 관련하여 불변함을 의미한다.

$x y'=displaystyle x'=syslogfrac {1}+y},\syslogfrac {1}{x}}}}})$

분명히 ST는 첫 번째 적분 H = 1/x + y를 갖는다.H = const δ c 라인에서 변환은 다음과 같은 형태를 가집니다.

${\[{\=\}}=leftrightdisplaystyle {\frac}}}{\left}}$

따라서 ST의 불변 측정 밀도는 다음과 같아야 한다.

$fdisplaystyle f(c)\\dc\frac {1}{x}\frac {leftf}{y}{right}$

대칭 P(x, y)= P(y, x)를 고려하면 f(c)= c가⁻² 되므로 (정규화 후)

$P P\left(x_{s}^{-}\frac {x}{-}{x+}\right}$

(예: 79g)

(x 또는^– x에 대한⁺ 적분은 함수 w(x) eq.74)를 산출한다).일대일 매핑으로의 변환의 감소는 체르노프와^[50] 바로에 의해 이미 사용되었으며, 그들은 eq. 79g의 공식을 얻었지만 다른 변수에는 적용하지 않았다. 그들의 논문은 Khalatnikov et al.^[49]에서 고려된 문제에 대한 적용을 포함하고 있지 않다.

eq. 79g의 정확성은 직접 계산으로도 검증된다. 변환 eq. 79e의 야코비안은

$J \right} {displaystyle J=frac \left(x_{s+1}^{-}\right}\fright}\fright}) {x}\fright} \fright}=frac {{frac x_{s+1}^{+}}{\frac {\frac x_{s+1}^{-}=\left frac {x_{s+1}^{+}}}}}{\frac {x_{{+}}}}}}}}}}}}}}}:{\frac {\frac xfrac {\frac xfrac}}}}{-}}}}:{frac}}}}}{frac {\frac}{frac}.$

(계산에서는 [${\displaystyle 1\mathrm{}}$ ${\displaystyle /}$ ${\displaystyle x_{}^{}}$s${\displaystyle {}_{}^{}}$+ ${\displaystyle ]}$+ {${\displaystyle }$1 / ${\displaystyle x_{}^{}}$s + ${\displaystyle {}_{}^{}}$ $=$ / ${\displaystyle x{}_{}^s}$+ { $displaystyle \left [1/x_{s}^{+}\right }+\$left$\{1/x_{s}^+}\right$임을 유의해야 합니다).

eq. 79d θ는_s 랜덤량⁺ x와⁻ x로 표현되므로 이들의 공동분포에 대한 지식은 변수 중 하나에 대해 P(x⁺, x⁻)를 θ의 상수값으로 적분함으로써 통계분포 P(θ)를 계산할 수 있다.변수⁺ x와⁻ x에 대한 함수 eq. 79g의 대칭성 때문에, 변수 x와 x에 대한 P(p) = P(1 - θ), 즉, 함수 P(p)는 점 θ = 1/2에 대해 대칭이다.그리고나서

$Pdisplay _1}left {\flac {-\flac {\ xflash \flightflash {x}}{flight}\flight}\flash {x}}}}{}}}}{\flight}}}}}}}}}}}}}}}$

적분(0 and 1/, 그 후 )을 으로 (0 ≤ 11과 1/2의 경우)는 1과 1/2로 한다

$P(\param +displaystyle P(\delta)=param frac {1}{\left(1-2\param +1\right)\ln2}}$

(예: 79시간)

함수 P의 대칭성으로 인해 $평균값{\displaystyle \stackrel{}{}}$1({style\$display\bar}})$ 1/2은 이미 표시되어 있습니다.따라서 함수 α, β, θ의 초기(모든 시대) 진폭이 δ/2만큼 증가한다.

큰 시간 간격 δ와 여기에 포함된 시대 수 사이의 통계적 관계는 eq.77을 반복 적용함으로써 찾을 수 있다.

$(\displaystyle {Omega ^{(0)}}=\exp \left(\sum _ {p=0}^{s-1}\xi ^{(p)}\exp ）}$

(eq.80)

그러나 이 방정식의 직접 평균화는 의미가 없습니다. 함수 W(k) eq.76의 느린 감소로 인해 수량 exp µ의^(s) 평균값은 위와 같은 의미에서 불안정합니다. 즉, 평균 영역이 증가함에 따라 평균값 자체보다 변동폭이 훨씬 더 빠르게 증가합니다.이 불안정성은 로그를 취함으로써 제거된다: "이중 로그" 시간 간격

${\^{{( - =\ _xi ^{p)}\equiv\frac\ln leftfr$

(eq.81)

는 안정적인 통계 분포를 갖는 수량 θ의^(p) 합으로 표현된다.τ의 평균값은 $\tau {\displaystyle \stackrel{}{}}$ ${\displaystyle =}$ ${\displaystyle s}$ ${\displaystyle display\stackrel{}{}}$display $display$ （ \ $displaystyle$$${ \$$$bar }$=$sbar$ { xi $}$$$） to${\displaystyle \stackrel{}{}}\xi {\displaystyle \stackrel{}{}}$ ξ$$ξ ξ ξ ξ ξ ξ ξ display $display can$ the$$ $can$ the the the the the the the s s s = s {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\

$\}\ln { \lefts)+}=\ln {frac \left(k_{s)+x_s}\right}_{s}_{s}\ln}_{s}_right}_{s}_right}_right}_right}_right}_{s}_right}_{s} _ (1-_}\right)=\ln {frac _ {s} {x_{s-1}\left (1-\frac _ {s+1}\fright$

(eq.81a)

${\displaystyle \stackrel{}{\mathrm{고정분포}}}$ ${\displaystyle \stackrel{}{{}_{}}}$ ${\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{x_{}}}$ s${\displaystyle \stackrel{}{{}_{}}=\stackrel{}{{}_{\mathrm{x}}}}$ s - 1$$$display$ $displaystyle$\ $displaystyle$ \ overline \ $ln x$_ { s - 1$$}$$${\displaystyle =}$ punction P ( s ${\displaystyle \stackrel{}{{\_}_{}}}$ { s - 1 ） $line$、 ${\displaystyle \stackrel{}{{ln}_{}}}$ s$$ $ln$ ${\displaystyle \stackrel{}{{\mathrm{s}}_{}}}$ +${\displaystyle \stackrel{}{}}$1$$）$$$}\right$ 따라서

$x)\\dx={62.}{\displaystyle {x}=-2 오인 { {ln x}^2\w}{\w}{{\ln}{{\w}{\ln}{\ln}{\ln}{{{\ln}}{{{{{{\ln}}}}}}{{{{{{$

(w(x)는 eq. 74부터).따라서

$displaystyle\displayline_{s}=2.37s,$

(예.82)

연속된 시대를 포함하는 평균 이중 전자 시간 간격을 결정합니다.

s가 클 경우, eq.81의 항 수는 크고, 에르고드 이론의 일반 이론에 따르면 are의_s 값은 밀도와 함께 gauss의 법칙에 따라 ${\displaystyle \stackrel{}{s_{}}}$ s${\$ (\style$\display\tau_{s}}})$ 주위에$$ 분포한다.

$_ _}\displaystyleft[styledisplaystyledisplaystyleface _s}$

(예: 82a)

분산_τ D의 계산은 $({$$$$})$ 및 $(\${\$xi$$$})에 대한 지식뿐만 아니라 $(\$2}})의 상관관계도$$필요하기 때문에 더욱 복잡하다.계산은 합계 81의 용어를 재정렬함으로써 단순화할 수 있다.eq.81a를 사용함으로써 합계는 다음과 같이 고쳐 쓸 수 있다.

$_{p}=\ \ _{p+1p-1 _}{}{p}{p}{p}{p}}}{p}}{frac}}{{{p}}}}}{p}}{p}}}}{p}}}}}}c _{p+1}\right)x_{p-1}=\ln \fln \frac_{p}{p}{p}{p}{p}{p}}{p}}{frac}{p}}}{p}}}{p}}}{p}}}{p}}}{p}}}{p}}}}}}{p-1}}}}}}}{p-1}}}}:$

마지막 두 항은 s가 증가할수록 증가하지 않습니다. 큰 s에 대한 제한 법칙이 지배적이므로 이러한 항은 생략할 수 있습니다.그리고나서

${p}^{+}}}{\displaystyle _{p}=\sum _p=1}^{{{{{p}}}{p}{p}{p}{p}}}}{\xi_frac}{{\x}{{\x}}{p}{p}}}{p}{x}}}}{x}}}}}{$

(예: 82b)

(eq_p. 79d라는 식도 고려된다.)동일한 정확도(즉, s와 함께 증가하지 않는 항까지) 동일성

$__{ _displaystyle \sum _{p=1}^{s}\xi _{p}^+}=\sum _{p=1}^{s}\xi_{p}^{-}^{-}$

(예: 82c)

유효합니다.실제로, eq.79e에 의해

$frac {pdisplaystyle x_{p+1}+{\frac {x+1}^{-}}{-}}}{-}}{-}}{-}}}{black {x}}}}}} {black {black {x}}}} {x_1}$

에, 「」라고 하는 것이 됩니다.

$1}^{-} \{p+1}^{-}\right)-ln x_{p+1}^{-}^{-}(왼쪽)^{-}^{-}\ln left}p}{-}\{px_{p}^-}\right)-\ln x_{p}^+}$

이 항등식을 페이지 82c에 합계하면 얻을 수 있다.마지막으로 동일한 $정확도{\displaystyle {}_{}^{}}$ ${\displaystyle x_{}^{}}$p$$+ {\$displaystyle x_{p}^{+}}$이(가) 합계 기호 아래의 x에 대해_p 변경되어 as가_s 다음과 같이 표시됩니다.

$_{_{_{p}=-displaystyle _{s}=\sum _{p=1}^{\infty}\eta _{p},\display \eta _eta {p}$

(eq.83)

큰 s의 한계에서 이 합계의 분산은 다음과 같다.

${{ {\^{bar }+fty}\}\leftwrightleftrain\leftmline- {\bar {eta}+2\sum {p=}^{\fty}\fty}\leftwright}\leftrain\leftmline$

(eq.84)

$시퀀스$ X의 통계적 동질성 때문에 $상관관계$는 p-p의$$차이에만 $의존$한다는 것을 $고려합니다.$평균값 $\eta {\displaystyle \stackrel{}{}}$ ${\displaystyle =}$ $display$ displaystyle ） = bar （ \ $displaystyle$ ） = bar （ \ $bar$ } ） = $bar$ （ \ $xi }$ $）$ ;평균제곱

${\displaystyle {\displaystyle {\displaystyle {\displaystyle displaystyle {\displaystyle {\ {{0(x _2x(x)\bln {$

또한 p = 1, 2, 3 (수치적으로 환산)의 상관치 ${\displaystyle \stackrel{}{{\eta \mathrm{}}_{}}}$ 0 ${\displaystyle \stackrel{}{p_{}}}$ p ${\$ { $displaystyle${$overline _${ $0$} $with$ { $p$} } with$$ with by_τs by ( D = ( 3.5 ± 0.1)s 를 구한다.

가 증가할 때 $상대변동{\displaystyle {}_{}}$ D ${\displaystyle \stackrel{}{s_{}}{{}_{}}_{}}$s / s ${\$ { $displaystyle D_{\tau }_{s}}/{\overline {tau$ _${s}}}$은 s로서^−1/2 0이 되는 경향이 있습니다.즉, 통계적 관계 eq.82는 큰 s에서 거의 확실해진다.이를 통해 관계를 반전시킬 수 있습니다. 즉, 이중 로그 시간의 주어진 간격 θ에서 상호 교환되는 에러_τ s의 평균 숫자에 대한 의존으로 나타낼 수 있습니다.

$}{\displaystyle {s_{\display}}= 0.47\display}$

(예.85)

평균 주위에 있는 s의 정확한_τ 값의 통계적 분포는 또한 분산과 함께 가우스이다.

$tauD_{\tau}=.5gfrac{\overline {s_{\tau}}}}={\displaystyle D_displaystyled}}}{{{{{{\t}}}}}}}}}}}}}}}}}}}{{{{{\cfrac}}}}}}}}$

각_τ 통계 분포는 랜덤 변수가 현재 주어진 θ에서 s인 동일한 가우스 분포에 의해 제공됩니다.

$\displaystyle \rho ( s _ { \ right } ) \ propto \ exp left \ { - \ left ( s _ { \ right } - 0 . 47 \ exp )^2} / 0 . 43 \ exp \ right \ } }$

(예.86)

이 관점에서 통계적 거동의 근원은 교환 시대의 무한 시퀀스에 중첩되는 구간 θ의 시작점 선택에서의 임의성이다.

물질 밀도와 관련하여, eq.79는 형식에서 eq.80을 고려하여 다시 작성할 수 있다.

$^{(}}=_{ _x}{x}}}}\Omega ^{(0)}\right]}$

그리고 시대별 총 에너지 변화에 대해

$\displaystyle \frac \varepsilon ^{(0)}=\ln \sum _{p=0}^{s-1}\exp \{\sum _{q=0}^{p}\xi _q}+\eta _{p}\right.}$

(eq.87)

합계가 p인 항은 이 식에 큰 검정력을 가진 지수를 포함하기 때문에 이 식에 주된 기여를 합니다.이 항만 남겨두고 평균 87항을 구하면 오른쪽에 eq.82와 일치하는 식 ${\displaystyle \xi \stackrel{}{}}$_s ${\$ s${\xi }}$가 나온다. 그 외의 모든 항은 상대적인 순서 1/s의 수정으로 이어진다.그러므로,

$^{(오른쪽)\displaystyle\ln\leftfrac{varepsilon ^{(0(\frak오메가right}}}}}}}{{\}}=는 (\ln \leftfrac {Omega ^{(s)}}}}\right)}}입니다.}$

(eq.88)

§와_s sq 사이의 관계의 거의 특정한 특성 때문에 88은 다음과 같이 쓸 수 있다.

$_^{(rightdisplaystyle \ln \left(\varepsilon _{\display}/\varepsilon ^{(displaysilon \left)\ln \lengthright(\ln \ln \ \ \lengtdisplaysilon \left= 2.1s,}$

이 값은 주어진 이중 주파수 시간 간격 θ 또는 주어진 에라 수 s에 의해 평균화된 밀도 증가의 이중 로그 값을 결정한다.

이러한 안정적인 통계 관계는 이중 대수 시간 간격과 밀도 증가에 특히 존재합니다.다른 특성, 예를 들어 ln(θ⁽⁰⁾/θ^(s)) 또는 δ^(s) / δ⁽⁰⁾ = exp δ의_s 상대적인 변동은 평균 범위의 증가에 따라 기하급수적으로 증가하여 안정적인 의미의 용어 평균값을 무효화한다.

통계 관계 eq.88의 기원은 개별 카스너 시대 동안 밀도 변동을 지배하는 초기 법칙에서 이미 추적할 수 있다.eq.21에 따르면, 우리는 진화 과정 동안

$= + \+ \ 2 } {\displaystyle \ln \varepsilon (t) = text {const} + \ln 2 (1-p_{3} (t)} ) ,$

1 - p₃(t)가 에폭에서 에폭으로 변경되어 0에서 1까지의 간격으로 값을 통과합니다.ln Ω = ln (1/t₃)이라는 용어는 단조롭게 증가하지만, ln2(1 - p)라는 용어는 p 값이 유니티에 매우 가까운(즉₃₁, 매우 작은 p) 경우에만 큰 값(ln Ω과 함께 사용할 수 있음)을 가정할 수 있습니다.이들은 정확히 77–eq 79와 같은 반복적인 관계에 의해 표현되는 진화의 규칙적인 과정을 방해하는 "위험한" 경우들이다.

그러한 사례가 실제로 점근 제한 체제에서 발생하지 않는다는 것을 보여 주는 것이 남는다.모델의 자발적 진화는 명확한 초기 조건이 임의의 방식으로 지정된 특정 순간에 시작됩니다.따라서, "점근성"은 선택된 초기 순간으로부터 충분히 멀리 떨어진 정권을 의미한다.

위험한 경우란 한 시대가 끝날 때 매개변수 u = x(따라서 p₁ ≤ x)의 지나치게 작은 값이 나타나는 경우이다.그러한 경우의 선택 기준은 불평등이다.

$x\alpha 1displaystyle x^{s}\exp \left \alpha ^{s}\right \lesssim 1,}$

(예.89)

여기서^(s) α는 시대 s에서 진동하는 함수의 초기 최소 깊이이다(최종 진폭을 선택하는 것이 더 적절하지만 선택 기준만 강화된다).

첫 번째 시대의 x 값은⁽⁰⁾ 초기 조건에 따라 결정됩니다.위험 값은 δx⁽⁰⁾ ~ exp ( - α⁽⁰⁾ )의 간격이며, 다음 시대에 위험한 경우를 초래할 수 있는 간격도 있습니다.x가 위험 구간 θx^(s) ~ exp ( -α^(s))에 속하기 위해서는^(s) 초기값⁽⁰⁾ x가 폭 θx⁽⁰⁾ ~ θx^(s) / k^{(1)^2} ... ^[51]k의^{(s)^2} 간격에 속해야 한다.따라서 x의 가능한⁽⁰⁾ 모든 값의 단위 간격에서 이 간격의 부분 θ에 위험 사례가 나타난다.

$^{( _}\ _^{(displaystyleft \exp \exp \left(\(\left -\alph ^{(\right)\xp ^(\sum {sum {sum } \xp } \sum {sum^{(1}}}}\k^{(2}}}}{k^{(1)^{2}}{(2)\colon k^{(s)^{2}}}}}$

(예. 90)

(내부 합계는 1에서 θ까지의 모든 값⁽¹⁾ k, k⁽²⁾, ..., k에^(s) 대해 취득됩니다).이 시대는 eq. 90의 첫 번째 항에 의해 크기 순서가 결정되는 값 ${\(\displaystyle\ll$$)$ 1로 수렴됨을 쉽게 알 수 있다.이는 시대⁽¹⁾ k⁽²⁾, k, ...의 길이에 관계없이 α = (s⁽⁰⁾ + 1) α로 치환하는^(s) 시대의 강력한 대명사로 입증될 수 있다(사실^(s) α는 훨씬 더 빠르게 증가하며, 가장 불리한 경우⁽¹⁾ k = k⁽²⁾ = k = ...= α의^(s) 1 값은 q > 1)에 따라 q α만큼 증가한다^s(0).

$\k^{((\pi2}/rightdisplaystyle _{k^{(1)^2}{{{2}}{{{{2}}}}}=\left(왼쪽)\displaystyleft(\sum {kk}{{{{k}{{{{{{{{{{{{{})})}}}}}}{{{{{{{{$

에 넣다

$\displaystyle \exp \left(\left -\alpha ^{(0)\right)\sum _{s=0}^{\infty }\left[\left(\pi ^{2}/6\right)\exp \left(\left -\alpha ^{(0)\right)\exp ]\exp ^{(\ref{(\right)\right)\left)\left)\ref{(\left)\left)$

초기값⁽⁰⁾ x가 위험영역 밖에 있으면 위험사례는 발생하지 않습니다.이 지역 내에 있는 경우 위험한 경우가 발생하지만, 완료 시 모델은 위험 간격에 가끔(확률 θ)만 들어올 수 있는 새로운 초기 값을 사용하여 "정기적인" 진화를 재개한다.반복적인 위험사례는 확률θ², θ³, ...이 점근적으로 0으로 수렴되는 상태에서 발생한다.

을 수반하는

위의 모델에서 특이점 근처의 메트릭 진화는 균질 공간 메트릭의 예에서 연구된다.이러한 진화의 특성에서 그러한 유형의 특이성에 대한 일반 해법의 해석적 구성이 각각의 기본 진화 요소에 대해 별도로 이루어져야 한다는 것은 명백하다. 즉, 카스너 시대의 경우, 두 가지 섭동 작용이 있는 장기간에 걸쳐 "격동"에 의해 야기된 에폭 사이의 전환 과정을 위해.동시에.카스너 시대 동안(즉, 작은 섭동 시), 메트릭은 조건 θ = 0 없이 eq. 7에 의해 주어진다.

BKL은 또한 작은 진동으로 장기간에 걸쳐 물질 분포 독립 모델(동질 또는 비동질)을 개발했습니다.이 솔루션의 시간 의존성은 동종 모델의 특정 경우와 매우 유사한 것으로 판명되었습니다.동종 모델은 분포 ^[52]독립 모델에서 포함된 임의 함수를 선택하여 얻을 수 있습니다.

그러나 동기 기준 프레임에서와 약간 다른 좌표계(g_0α = 0)에서 일반 해를 구성하는 것이 편리하지만, 이제₀₀ g = 1 대신₀₀ g = -g가₃₃ 된다.공간 메트릭 텐서 θ_αβ = -g_αβ one을 다시 정의하면 다음과 같이 된다.

$\displaystyle g_{00}=\display_{33,\display g_{0\alpha}=0.}$

(eq.91)

특수 공간 좌표는 x³ = z, 시간 좌표는 x = ((적절한 시간 t와 다름)로⁰ 작성됩니다. cor는 동종 모델에서 정의된 변수와 일치함을 나타냅니다.θ, z에 의한 미분은 각각 도트, 소수에 의해 지정된다.라틴 지수 a, b, c는 공간 좌표¹ x, x에² 대응하는 값 1, 2를 취하며, x, y로도 작성됩니다.따라서 메트릭은

$\displaystyle ds^{2}=\display_{33)\left(d\xi ^{2}-dz^{2}\right)-\display_{ab}display_{b}-2\display_{a}dz.}$

(eq.92)

.

$}\ll \displaystyle _{33}\ll \displaystyll \displaystyle _{ab}$

(eq.93)

$\displaystyle _{displaystyle _{a}\displaystyle _{a}\displaystyle _{339}$

(예.94)

(이러한 조건은 a, b², c² 중 하나의 함수가² 다른 두 개에 비해 작음을 명시하며, 이는 균질 모델에서도 마찬가지이다.)

부등식 eq.94는 공간길이요소² dl의 제곱에서 시프트^a dx, dz의 임의의 비율에 따라 곱^a dxdz와의 항을 생략할 수 있다는 점에서 성분θ가_a3 작다는 것을 의미한다.따라서 용액에 대한 첫 번째 근사치는 θ_a3 =^{[note 19]} 0인 메트릭 eq 92이다.

$\displaystyle ds^{2}=\display_{33)\left(d\xi ^{2}-dz^{2}\right)-\display_{ab}ds^{a}display^{b}display^{b}display^{b}display^{b}display^{b}.}$

(예 95)

Ricci 텐서 $성분{\displaystyle {}_{}^{}}$ ${\displaystyle {R\mathrm{}}_{}^{}}$ $($ 스타일 $R_{0}^0$ $R{\displaystyle {}_{}^{}}$ $3{\displaystyle {}_{}^{}}$$($${\displaystyle {\mathrm{}}_{}^{}}$ $스타일 R_${3$}^$$0$}),$$R $($ R_{$3}^3$ R ${\displaystyle {}_{}^{}}$ b$($ R_${a}^{b})$는 메트릭 eq 95 및 모든 조건을 사용하여 쉽게 계산할 수 있습니다.nates^a x는 도함수 항에 비해 θ 및 z만큼 작습니다(비율은 ~ θ₃₃ / θ_ab).즉, 주근사 방정식을 구하려면 eq. 95의 θ와₃₃ θ를_ab x에 의존하지^a 않는 것처럼 미분해야 한다.

$^{\psi\prime}^{ _displaystyle _{33)={dotsi}, {dot$

(예.96)

다음 방정식을 ^{[note 20]}구합니다.

$2e}\rightprimeright)\psi 스타일 2e 1}$

(eq.97)

$^{\}R_{3}^{0}=varkappa ^{\prime}+{\frac {1}{2}}\docda {{prime}-\varkappa ^{b}_da{b}$

(98호)

$({displaystyle 2e^{\psi }(R_{0}^0}-R_{3}^{3})=\lambda \psi ^{\prime}+\varkappa {dot {psi }-{\prime}-{\prime}-{\primeq } ^{{{{{{\pa} } } } } } } } } } } - \pa ^{{\pa } } } } }$

(eq.99)

여기서 지수 상승과 하강은 γ의_ab 도움을 받아 이루어집니다.$수량{\displaystyle }${\({$displaystyle\varkappa})$ 및$$ ${\displaystyle {are}_{}^{}}$({displaystyle\$varkappa_{a}^$a$$$})$은 수축$$(\$displaystyle\varkappa_${a$})$ 및$(\$}^{a}^{a})입니다$$.

$\displaystyle \varkappa = 2dot {G}}/G, \display \dotsda = 2G^{\prime }/G.}$

(eq.100)

Ricci 텐서 $성분{\displaystyle {}_{}^{}}$ $R$은 0$({$displaystyle $R_{a}^0$ ${\displaystyle {}_{}^{}}$은 3$({$으로 계산하면 0이 됩니다.다음 근사치(즉, 작은 θ_a3 및 x, y에 의한 도함수)에서는 이미 알려진 θ₃₃ 및 θ에_ab 의해 수량 θ를_a3 결정한다.

eq.97의 수축은 G ${\displaystyle {\prime \mathrm{}}^{}g\stackrel{}{}}$ + G $=$ 0 {\$displaystyle G^{\prime$ \prime$}+{\dot$ {$G}=$0$\}$이므로 $다음$과 같다.

$\displaystyle G=f_{1}(x,y,\xi +z)+f_{2}(x,y,\xi -z)}$

(eq.101)

G 변수에 따라 다른 경우가 발생할 수 있습니다.위의 경우⁰⁰ g = γ$$γ³³ \ $displaystyle \gg }$ $n$^ab n ${\displaystyle {}^{}{00}^{}{}^{}{}^{}}$g ${\displaystyle {00\stackrel{}{}}^{}}$ ( G${\displaystyle {{}^{}}^{\mathrm{}}}$ ${\displaystyle {}^{}{}^{}{}^{}2}$ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}{\stackrel{}{}}_{}}$ 33 f${\displaystyle {\stackrel{}{}}_{}{\stackrel{}{}}_{}}$ 1 ${\$ 2 \ $displaystyle N$ \ g \$g \ dot$ { $G$} \ $gam ^2$ - （ $G$）대소문자 N > 0(수량 N은 시간과 유사함)은 관심있는 시간 특이점으로 이어집니다.101 f₁ = 1/2 (표준 + z) sin y, f₂ = 1/2 (표준 - z) sin y로 치환하면 G형이 된다.

$G= ydisplaystyle G=\xi \sin y.,}$

(eq.102)

이 선택은 결론의 일반성을 감소시키지 않는다. 변수의 나머지 허용 가능한 변환 때문에 일반성이 (첫 번째 근사치) 가능하다는 것을 보여줄 수 있다.N < 0(N은 우주와 유사함)에서 잘 알려진 아인슈타인-로젠 ^[53]메트릭을 일반화하는 G = z로 대체할 수 있다.N = 0일 때 δ + z 또는 δ^[54] - z에만 의존하는 로빈슨-본디 파동 메트릭에 도달한다(cf).eq. 102의 계수 sin y는 동종 모델과 쉽게 비교할 수 있도록 배치되었다.eq. 102를 고려하여 eq. 97 – eq.99 공식은 다음과 같다.

$^{-1}\display {dot {varkappa}}^{b}+\xi ^-1}^{b}^{b}^{b}^{a}^{a}^{a}^{a}^{a}^{a}^{a}^{a}^{a}^{a}^{a}^{a}{a}{a}$

(예 103)

$(\displaystyle {dot {psi }}=-\xi ^{-1}+{\frac {1}{4}\xi \left(\varkappa _{a}^{b}+\b}\parcappa _{a}^{a}\parcda}\오른쪽).}$

(예 104)

$\displaystyle \psi ^{\prime}=snapfrac {1}{2}\xi _{a}^{b}\snapda _{b}^{a}.}$

(eq.105)

주요 방정식은 θ_ab 성분을 정의하는 eq.103이다. 그러면 eq.104–eq.105의 단순한 적분으로 함수 θ를 구할 수 있다.

변수 " 는 0 ~ " 의 값을 통과합니다.eq. 103의 솔루션은 $§$ {$displaystyle$$$\$gg$ $}$ 1과$§$ {$displaystyle$ \ll$$ $}$ 1의 두 가지 경계로 간주됩니다.큰 θ 값에서는 1 / θ 분해 형식을 취하는 솔루션을 찾을 수 있습니다.

$displaystyle _{ab}=\xi \left[a_{ab}(x,y,z)+O(1/{\sqrt {xi}}}}\right}\right})\right],$

(106호)

때문에

$=displaystyle a_{ab} =\sin ^{2}y,}$

(eq.107)

(제107호는 조건 102가 참이어야 합니다).eq.106의 eq.103을 대체하면 첫 번째 순서로 얻을 수 있다.

$)(\displaystyle\lefthava^{ac}^{\prime}a_{bc}\primeprime}=0,}$

(예 108)

여기서 수량^ac a는 행렬_ac a와 역행렬을 구성합니다.eq. 108의 해법은 다음과 같은 형태를 가진다.

$^{-2\ z zdisplaystyle a_{ab}=l_{a}l_{b}e^{-2\rho z}_{b}z}z^2}{displaystyle$

(예 109)

$1} y,}{\displaystyle l_{1}m_{2}+l_{1}=\sin y,}$

(예: 110)

여기서_a l, m_a, θ는 eq. 107에서 도출된 조건 eq. 110에 의해 결합된 좌표 x, y의 임의 함수이다.

이 분해의 더 높은 항을 찾으려면 필요한 양의 행렬을 in_ab 형식으로 쓰는 것이 편리하다.

$ab\leftL}edisplaystyle _{ab}=\xi \left\tilde {L}ab}L\right}L_{ab}_{ab}$

(예 111)

$L z zdisplaystyle L=bmatrix{1}e$

(예: 112)

여기서 ~ 기호는 행렬 전이를 의미합니다.행렬 H는 대칭이며 그 배선은 0입니다.제시 eq.111은 θ의_ab 대칭성과 조건 eq.102의 충족을 보장한다.exp H를 1로 치환하면 eq.109에서 a로_ab eq.111 γ_ab = aa를_ab 구한다.즉, γ_ab 분해의 첫 번째 항은 H = 0에 해당하며, 성분이 작은 행렬 H의 거듭제곱 분해에 의해 더 높은 항이 얻어진다.

행렬 H의 독립적 성분은 다음과 같이 θ 및 θ로 작성됩니다.

$(\displaystyle H=bmatrix\sigma &\varphi &-\displaystyle \end{bmatrix}).}$

(예: 113)

eq. 103의 eq. 111을 대체하고 선형 용어만 H로 남기면 θ와 θ를 도출할 수 있다.

${\^{-prime displaystyle \ \prime } + \xi ^ {-1} {\prime } = 0,}$

${\displaystyle {\varphi }+\xi ^{-1}{\dot {\varphi }}-\varphi ^{\prime }+4\rho ^{2}\varphi = 0.}$

(예 114)

이들 방정식의 해법을 z좌표로 푸리에 급수로서 구하려고 하면 θ의 함수로서 베셀 방정식을 구한다.큰 θ에서^{[note 21]} 솔루션의 주요 점근 항은 다음과 같다.

$\}\_{-\}^{\}\ope }e^{-displaysty }\displaysty }\displaysty }\displaysty styledisplaystyledisplaystyledis$

$\ {\{\} {n=-\}^{\ \}\right)in} styledisplay {\p}$

(eq.115)

$\displaystyle _{n2}^{2}=n^{2}\display ^{2}+4\rho ^{2}.}$

계수 A 및 B는 좌표 x, y의 임의의 복소함수이며, 실수 θ 및 실수 θ에 대해 필요한 조건을 만족한다.기준 주파수 θ는 x, y의 임의의 실수함수이다.이제 eq.104~eq.105부터는 함수 θ의 첫 번째 항을 쉽게 구할 수 있다.

$\psi^{^{displaystyle \psi =\rho ^{2}\xi ^{2}}$

(예: 116)

(이 항은 θ = 0이면 사라진다. 이 경우 주항은 분해에서 θ = θq(x, y)의 선형이다.) 여기서 q는 양의^[56] 함수이다.

따라서 큰 δ값에서는 eq. 111의 감소하는 δ인자에 의한 느린 감소의 배경에 따라 δ감소에 따라 메트릭텐서 δ성분이_ab 진동한다.성분 θ₃₃^ψ = e는 exp(exp²²)에 가까운 법칙에 의해 빠르게 감소하며, 이는 조건 eq.[note 22]93을 가능하게 한다.

다음 BKL에서는 대소문자 $"\displaystyle\ll$$"$ 1을 검토합니다.eq. 103의 솔루션에 대한 첫 번째 근사치는 좌표별 도함수에 대한 이러한 방정식에서는 생략할 수 있다는 가정에 의해 결정된다.

${\displaystyle {{varkappa}_{a}^{b}+\xi^{-1}\varkappa_{a}^{b}=0.}$

(예: 117)

이 방정식은 조건 eq 102와 함께 다음과 같다.

$_{displayda _{displaystyle _{}=\displayda _{b}\xi ^2s_{b}_{b} _b}$

(eq.118)

여기서 θ_aa, μ, s₁, s는₂ 다른 조건과 관련된 3개의 좌표 x, y, z의 임의의 함수이다.

$_{2 _{1}-{2 _{1}-\synda _{1}-\synda _{1}-\synda _{2},\$

(예: 119)

방정식 eq.104–eq105는 지금 제시된다.

$=e^{\ \xi ^{-(}-2}^{2displaystyle _{33)=e^{\psi }\sim \xi ^{-(1-s_{1}^2}-s_2})$

(eq.120)

eq. 118로 계산한 도함수 ${\displaystyle {a_{}^{}}^{}}$ $({$style$\display\lambda_{a}^{\prime$는 ~ and과^{4s₁ − 2} ξ를^{4s₂ − 2} 포함하며, eq. 117에 남은 항은 ~ ξ이다⁻².$따라서$ eq. 117 대신 eq. 103의 적용은 s > 0, s₂ > 0 조건에서 허용된다₁. 따라서 1 - ${\displaystyle {}_{}^{}}$ $1{\displaystyle {}_{\mathrm{}}^{}}$ - s$$ {{$1}^{2}-s_{2}^{2}}$ > 0이다.

따라서 작은 oscill에서는 함수 cease의_ab 진동이 정지하고 ξ의 감소 ξ에서₃₃ 함수 begins의 진동이 증가하기 시작한다.이것은 Kasner 모드이며, 「」를₃₃ 「」와_ab 비교하면, 상기의 근사치는 적용되지 않습니다.

이 분석의 적합성을 확인하기 위해 BKL은 ${\displaystyle R_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$0 {\$displaystyle R_{\alpha$}^{$0$$}$ =$$ 0, ${\displaystyle R_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$3 {\displaystyle $R_{\alpha$}^{3$}}$ =$$ 0 $등식$을 연구하여 성분 θ를_a3 계산하여 부등식 eq 94가 발생함을 확인했다.이^[52] 연구에서는 두 점근 영역 모두에서 성분_a3 θ가 ~ θ인₃₃ 것으로 나타났다.따라서 불평등의 정확성은 즉시 불평등의 정확성을 의미한다.

이 해는 진공상태의 필드의 일반적인 경우와 마찬가지로 3개의 공간 좌표 x, y, z의 4개의 임의의 함수를 포함한다.지역 ξ$$displaydisplaydisplay （ \ $display$style \$ll ）$1$$ 에서는, 이러한₁ 함수는₂ 「 」, 「 」, 「 μ₁₁」, 「s」 등입니다.영역 ξ$\gg {\displaystyle }$ ≫ （ \ $displaystyle \gg ）$1에서$$ 4개의 함수는 eq. 115부터 x, y의 함수의 좌표 z에 의해 푸리에 급수에 의해 정의된다.푸리에 급수 분해(또는 적분?)는 특수한 함수 클래스의 특성을 가지지만, 이 클래스는 모든 집합의 유한 서브셋을 포함할 수 있을 정도로 충분히 크다.가능한 초기 조건.

해는 또한 좌표 x, y의 다른 많은 임의 함수를 포함한다. 그러한 2차원 임의 함수는 일반적으로 나타나는데, 아인슈타인 방정식의 해에서 3차원 함수들 사이의 관계가 (대수가 아닌) 미분이기 때문에, 지오메에 대한 더 깊은 문제는 제쳐두고 있다.이러한 함수의 tric 의미.BKL은 독립적인 2차원 함수의 수를 계산하지 않았다. 왜냐하면 이 경우 3차원 함수는 2차원 함수의 집합으로 정의되기 때문이다(자세한 ^{[note 23]}내용은 참조).^[52]

마지막으로, BKL은 일반 솔루션이 동종 모델에 대해 위에서 얻은 특정 솔루션을 포함하고 있음을 나타냅니다.

이 모델의 시공간 메트릭은 eq.7에서 Biancchi Type IX 균질공간에 대한 기저 벡터를 대체한다.

$displaystyle ds_{IX}^{2}=dt^{2}-\left[\left(a^{2}\sin^{2}z+b^{2]}\cos ^{2}z\right)\sin ^{2}y+c^{2}\cossin^{2}-y}\cos ^{2}-\right]cos ^{2}\ ^{2}-y}$ $\displaystyle \left(b^2}-a^{2}\right)\sin {2z}\sin {y}\cos {y}\dxdz.}$

(예 121)

c $≪$ \ $displaystyle \ll }$ $a$², b일² 경우² c dz라는² 용어를² 제외하고 모든 장소에서 c를 무시할² 수 있습니다.eq. 121에서 사용하는 동기 프레임에서 조건 eq. 91의 프레임으로 이동하려면 변환 dt = c dθ/2 및 치환 z → z/2를 실행한다.또한 χ ln ln ln (a/b) $\{\backslash {\displaystyle }${ $displaystyle \ll$ $}$ 1이라고 가정하면 첫 번째 근사치에서는 eq. 121에서 다음과 같이 구할 수 있다.

$displaystyle ds_{IX}^{2}=tfrac {1}{4}c^{2}\left(d\xi ^{2}-dz^{2}\right)-ab\left\{\sin ^{2}{y}\left(1-chi \cosz}\right)\sin^{2}+(2ci}}}}$

(예 122)

는 마지지,, 비앙치 similarly VIIIIIIII, 음음음이다.

$displaystyle ds_{VII}^{2}=tfrac {1}{4}c^{2}\left(d\xi ^{2}-dz^{2}\right)-ab\left\{\sin ^{2}{y}\left(\operatorname {ch}z-chi\right)\left(\operatorname {ch}zch}zchi\left)\left(\left)}$

(예.123)

위의 균질 공간 분석에 따르면, 두 경우 모두 ab = ( (${\displaystyle {\mathrm{}}_{}^{}}$ ${$}^{2}} =$$ )) 및 is는₀ eq. 51에서 나온 것이며, 함수 c())는 각각 식 eq. 53 및 eq. 61에서 주어진다.

유형 VII에 대한 동일한 메트릭은 형식에서 2차원 벡터_a l과_a m을 선택하는 eq.112, eq.115, eq.16에서 구한다.

$}=}=m_{1}=sinfrac {{1}=sinfrt {2}}, {\ l_{1{\rt}, {\}, {y2}}, {y}, {y}, {y}, {y}, {y}, {y}, {y}, {y}, {y},$

(예.124)

$(\displaystyle \rho = btfrac {1}{2},\display A_{20}^{*}=iAe^{i\xi_{0}},\display A_{1n}=A_{2n}=B_{1}=B_{2}=0\adqne(0ne)}}}}}}})$

(예.125)

IX의 하려면 , 「IX」로 치환할 필요가 .

$==displaystyle \rho = 0,\obega = 1,}$ $=}^{*}=-{\{}=-{{2display style A_{11}=-B_{11}-{1,-1}=-{1}=-{{\frac {1}-}$ $}^{*}=}=-{\displaystyle A_{21}=B_{21,-1}^{2}={2},{2}_2}$ $}=}=}= 0displaystyle A_{1n}=A_{2n}=0\quadn(\neq \pm 0)})$

(126)

(c(c)의 계산의 경우, eq. 116의 근사치가 충분하지 않고, θ에 의한 θ의 선형 항이^[56] 계산된다.)

이 분석은 빈 공간에 대해 수행되었습니다.물질을 포함한다고 해서 해답이 일반적이지 않고 질적 ^[56][52]특성이 변하지 않습니다.

일반적인 솔루션에서 매우 중요한 한계는 메트릭 eq. 122와 eq. 123에 포함된 모든 3차원 함수가 단일하고 공통적인 특성 변경 간격을 가져야 한다는 것이다.이것만이 아인슈타인 방정식에서 모든 미터법 공간 성분 도함수와 이들 성분의 단순한 곱을 갖는 특성 파수 근사치를 허용하고, 이는 타입 IX 균질 모델에 대해 얻어진 유형의 일반 미분 방정식을 낳는다.이것이 동종 솔루션과 일반 솔루션이 일치하는 이유입니다.

따라서 타입 IX 모델과 그 일반화에는 물리적인 조건에 의해 선택되지 않은 임의의 크기의 단일 공간 스케일의 발진 모드가 포함된다.그러나 자유도가 무한한 비선형 시스템에서는 이러한 모드가 불안정하고 작은 진동으로 부분적으로 소멸되는 것으로 알려져 있습니다.임의의 스펙트럼을 갖는 작은 섭동의 일반적인 경우, 그 진폭은 항상 전체 프로세스 에너지를 증가시킵니다.그 결과, 일정한 에너지 분포와 다른 규모의 진동 사이의 에너지 교환에 의한 다단계 움직임의 복잡한 그림이 발생한다.물리적인 상황으로 인해 소규모 진동이 불가능한 경우에만 발생하는 것은 아닙니다.후자의 경우 동적 자유도를 가진 시스템에서 에너지가 나가는 최소 규모를 결정하는 자연 물리적 길이가 존재해야 합니다(예를 들어 특정 점도를 가진 액체에서 발생합니다).그러나 진공상태에서 중력장에 대한 타고난 물리적 스케일이 없기 때문에 임의로 작은 ^[57]스케일의 진동 발생에 지장은 없다.

★★★★★★★★★★★★★★★★★」

BKL은 복잡한 진동 특성을 가진 아인슈타인 방정식의 우주론적 해법의 특이점을 묘사합니다.이러한 특이점들은 주로 공간적으로 동질적인 모형들에 대해 연구되어 왔지만, 아인슈타인 방정식의 일반 해법의 특이점들이 같은 특성을 가지고 있다고 가정할 수 있는 설득력 있는 이유들이 있다; 이러한 상황은 BKL 모델을 우주론에 중요하게 만든다.

이러한 진술의 근거는 특이성에 대한 접근에서 진동 모드가 일반화된 카스너 솔루션의 불안정성을 야기하는 단일 섭동에 의해 발생한다는 사실이다.모델의 일반성에 대한 확인은 작은 진동을 수반하는 장기간의 해석 구조입니다.이 후자의 동작은 특이점에 가까운 메트릭 진화의 필수 요소는 아니지만, 모든 주요 정성적 특성을 가지고 있습니다. 즉, 2개의 공간 차원에서의 메트릭 진동과 일정 시간 간격의 끝에 이 모드의 특정 섭동을 수반하는 3차원의 단조로운 변화입니다.그러나 비균질 공간 메트릭의 일반적인 경우 카스너 시대 사이의 전환은 자세히 설명되지 않았다.

특이성에 의해 야기될 수 있는 공간 기하학의 한계와 관련된 문제는 추가 연구를 위해 남겨두었다.그러나 원래 BKL 모델이 유한 또는 무한 공간에 모두 적용 가능하다는 것은 처음부터 분명합니다. 이는 닫힌 공간과 열린 공간 모두에 대한 진동 특이점 모델의 존재로 증명됩니다.

특이성에 대한 접근의 진동 모드는 '시간의 최종성'이라는 용어에 새로운 측면을 부여합니다.세계 시간 t의 유한 모멘트와 t = 0 모멘트 사이에는 무한한 수의 진동이 존재합니다.이러한 의미에서 프로세스는 무한 특성을 획득합니다.시간 t 대신 ln t로 설명하는 것이 더 적절한 변수입니다.이것에 의해 프로세스가 -로 확장됩니다$.\$ $display$- \ $infty$ $。{\displaystyle }$

BKL은 시간을 단축하는 방향으로 메트릭의 진화를 고려합니다.아인슈타인 방정식은 시간 부호에 대해 대칭이기 때문에 시간이 증가하는 방향으로의 미터법 진화가 동등하게 가능하다.그러나 물리적 의미에서 과거와 미래는 동일하지 않기 때문에 이 두 사례는 근본적으로 다르다.미래의 특이성은 이전 순간에 존재하는 임의의 초기 조건에서 가능한 경우에만 물리적으로 의미가 있을 수 있습니다.우주의 진화에 있어서의 어떤 순간의 물질 분포와 장은 아인슈타인 방정식에 대한 주어진 특별한 해법의 존재에 필요한 특정한 조건과 반드시 일치하는 것은 아니다.

현실 세계에 대응하는 해법의 선택은 기존의 상대성 이론만으로는 찾을 수 없고 향후 물리 이론의 통합의 결과로 발견될 수 있는 심오한 물리적 요구와 관련이 있다.따라서, 이 선택은 특별한 (예를 들어 등방성) 유형의 특이점을 골라내는 것으로 밝혀질 수 있다.그럼에도 불구하고, 그 일반적인 특성 때문에, 진동 모드는 초기 진화 단계의 주요 특성이 되어야 한다고 가정하는 것이 더 자연스럽다.

이 점에서 상당한 관심사는 미스너가 ^[58]제시한 광신호의 전파와 관련된 "믹스마스터" 모델의 특성이다.등방성 모델에서는 "빛 수평선"이 존재하는데, 이는 각 시간의 순간마다 광신호의 교환이 불가능하고, 따라서 인과적 연결도 불가능하다는 것을 의미한다. 즉, 신호는 특이점 t = 0 이후 시간 동안 그러한 거리에 도달할 수 없다.

신호 전파는 ds = 0이라는 식에 의해 결정됩니다.특이점 t = 0에 가까운 등방성 모델에서 구간 요소는 d ${\displaystyle {s\mathrm{}}^{}}$ 2 $=$ ${\displaystyle {}^{}}$ t${\displaystyle {}^{}{2\mathrm{}}^{}}$ - ${\displaystyle 2}$ ${\displaystyle t}$ ${\displaystyle {\stackrel{}{}}^{}}$ l${\displaystyle {\stackrel{}{}2}^{\mathrm{}}}$2 { $displaystyle$ ds$^{2}$${\displaystyle 2^{\mathrm{}}}$ $2 {\$ 2 \ $display$ style ds^{$l}$ {l} {2$}}$。$여기$서 ${\displaystyle {\stackrel{}{}}^{}}$ds 2 \ display $style dispar$ {$l}$ {$l} ^{$2$$}}} 2 2 2 2 2 a a different different different different different different different different different different different different 2 different 2$$^[59]different different $different{\displaystyle }$$t{\displaystyle }$ $=$ ${\displaystyle {2\mathrm{}}^{}}$2 /$$ (\$displaystyle$ t=\$eta ^{2}/2$)의$$ 수율을 대입하면

$(\displaystyle ds^{2}=\eta ^{2}\left(d\eta ^{2}-dscar {l}}^{2}\오른쪽).}$

(eq.127)

신호에 의해 도달되는 "거리" ${\displaystyle \delta \stackrel{}{}}$ l$$δ {$displaystyle \Delta {l}}$은(는) 다음과 같습니다.

$(\displaystyle\Delta {l}}=\Delta \eta .}$

(예.128)

는 t와 마찬가지로 0부터 시작하는 값을 통과하기 때문에 "순간"까지의 신호는 호라이즌까지의 가장 먼 거리를 고정하는 거리 ${\displaystyle \delta }$ l${\displaystyle \stackrel{}{}}$¯$$（ \$display$ \ $Delta$\ $bar$ { $l }$ \ $leq \eta$ $}$ 에서만 전파할 수 있습니다.

등방성 모델에서 광선 지평선의 존재는 잔류 방사선에서 현재 관측된 등방성의 기원을 이해하는 데 문제를 일으킨다.등방성 모델에 따르면 관측된 등방성은 서로 인과적으로 연결할 수 없는 공간의 영역에서 관측자에게 도달하는 방사선의 등방성을 의미한다.특이점 근처의 진동 진화 모델에서 상황은 다를 수 있습니다.

예를 들어 타입 IX 공간의 균질 모델에서는 긴 시간 동안 스케일이 ~t에 가까운 법칙으로 변화하는 방향으로 신호가 전파됩니다.이 방향의 거리 요소의 제곱은² ${\displaystyle {dl\mathrm{}}^{}}$ = t² ${\displaystyle {\stackrel{}{}2}^{\mathrm{}}}$2({$displaystyle {l}^2}$） 、 4차원 간격의 각 요소는 d s 2 ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ t${\displaystyle {}^{}{2\mathrm{}}^{}}$ - ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle l^{\mathrm{}}}$ ${\displaystyle {\stackrel{}{†}}^{}}$2({$display$ ds$^{2} = dt^{2$} {\$bar {l}^2}$ } ^$2{\displaystyle }$} {2} }$$$2$ 2 。$대체{\displaystyle }$ t ${\displaystyle =}$ ${\displaystyle e^{}}$ ${\$ { $displaystyle$ t$=e^{\eta$}}은$$(는) 다음과 같이 입력합니다.

$({displaystyle ds^{2}=e^{2\eta}\left(d\eta ^{2}-dscapbar {l}^{2}\right),}$

(예.129)

신호 전파에 대해서는 다시 eq.128 유형의 방정식이 있습니다.중요한 차이는 변수 runs이 -${\$부터 시작하는 값(측정지표 eq. 129가 t = 0부터 시작하는 모든 t에 대해 유효한 경우$)$을 통해 실행된다는 것입니다.

따라서 주어진 각 "순간" δ에 대해 신호가 각 유한 거리를 커버하기에 충분한 중간 간격 δ δ δ가 발견됩니다.

이와 같이 오랜 기간 동안 주어진 공간 방향으로 빛의 지평선이 열립니다.각각의 긴 시대의 지속 시간은 아직 유한하지만, 세계 진화 시대의 과정 동안 다른 공간 방향으로 무한히 변화합니다.이러한 상황은 이 모델에서 전체 공간의 사건들 사이의 인과 관계가 가능할 것으로 예상하게 만든다.이러한 특성 때문에 미스너는 이 모델을 반죽을 만드는 기계의 브랜드 이름으로 "믹스마스터 유니버스"라고 명명했다.

시간이 흘러 특이점을 벗어나면 진화 초기에는 대수롭지 않았던 물질이 미터법 진화에 미치는 영향이 점차 커져 결국 우세해진다.이 효과는 우주의 현재 상태를 적절히 설명하는 프리드먼 모델에 그 특성이 더 가까운 점진적인 "등각화"로 이어질 것으로 예상할 수 있다.

마지막으로, BKL은 기존의 상대성 이론에 근거해 무한히 밀도가 높은 물질을 가진 세계의 "단일 상태"를 고려할 수 있는 가능성에 대한 문제를 제기한다.이러한 조건에서 아인슈타인 방정식의 현재 형태의 물리적 적용은 미래의 물리 이론의 통합 과정에서만 명확해질 수 있으며, 이러한 의미에서 현재로선 문제를 해결할 수 없다.

중력 이론 자체가 어떤 물질 밀도에서도 논리적 응집력을 잃지 않는 것이 중요하다.다시 말해, 이 이론은 논리적으로 허용되지 않고 매우 큰 밀도에서 그것의 적용을 논쟁적으로 만들 수 있는 조건에 의해 제한되지 않습니다; 원칙적으로, 제한은 중력 이론의 "외부" 인자의 결과로만 나타날 수 있습니다.이러한 상황은 우주론 모형의 특이점 연구를 공식적으로 받아들일 수 있게 만들고 기존 이론의 틀에서 필요하다.

메모들

레퍼런스

참고 문헌