데카르트 좌표계
Cartesian coordinate system평면 내의 데카르트 좌표계(영국: /kːtizzjn/, 미국: /kːrˈtiʒn/)는 동일한 길이의 단위로 측정된 2개의 고정 수직 지향선에서 점까지의 부호 거리인 한 쌍의 숫자 좌표로 각 점을 고유하게 지정하는 좌표계이다.각 기준 좌표선을 시스템의 좌표축 또는 단순 축(복수축)이라고 하며, 이들이 만나는 지점이 순서 쌍(0, 0)에서 원점이 됩니다.좌표는 원점으로부터의 부호 거리로 표현되는 두 축에 대한 점의 수직 투영 위치로 정의할 수도 있습니다.
동일한 원리를 사용하여 3차원 공간의 임의의 점의 위치를 3개의 데카르트 좌표로 지정할 수 있으며, 상호 수직 평면(또는 동등하게 3개의 상호 수직 선에 대한 수직 투영에 의해)에 대한 부호 거리를 지정할 수 있습니다.일반적으로, n 데카르트 좌표(실제 n-공간의 요소)는 임의의 차원 n에 대해 n차원 유클리드 공간의 점을 지정한다.이러한 좌표는 부호까지 점에서 서로 수직인 n개의 초평면까지의 거리에 동일하다.
17세기 르네 데카르트에 의한 데카르트 좌표의 발명은 유클리드 기하학과 대수학 사이의 최초의 체계적 연결을 제공함으로써 수학에 혁명을 가져왔다.데카르트 좌표계를 사용하여 기하학적 형상(곡선 등)은 데카르트 방정식으로 설명할 수 있습니다. 즉, 도형에 놓여 있는 점의 좌표를 포함하는 대수 방정식입니다.예를 들어, 평면의 원점을 중심으로 반지름 2의 원을 좌표 x와 y가 방정식2 x + y2 = 4를 만족하는 모든 점의 집합으로 설명할 수 있습니다.
데카르트 좌표는 해석 기하학의 기초이며, 선형 대수, 복소 해석, 미분 기하학, 다변량 미적분, 군 이론 등과 같은 수학의 많은 다른 분야에 계몽적인 기하학적 해석을 제공합니다.익숙한 예로는 함수의 그래프 개념을 들 수 있습니다.데카르트 좌표는 천문학, 물리학, 공학 등 기하학을 다루는 대부분의 응용 분야에 필수적인 도구이기도 합니다.컴퓨터 그래픽스, 컴퓨터 보조 기하학 설계 및 기타 기하학 관련 데이터 처리에 사용되는 가장 일반적인 좌표계입니다.
역사
데카르트라는 형용사는 프랑스의 수학자이자 철학자인 르네 데카르트를 가리키며, 그는 네덜란드에 거주하던 1637년에 이 생각을 발표했다.그것은 페르마가 [1]발견을 발표하지는 않았지만, 3차원으로도 작업한 피에르 드 페르마에 의해 독립적으로 발견되었다.프랑스의 성직자 니콜 오렘은 데카르트와 페르마의 [2]시대보다 훨씬 전에 데카르트 좌표와 유사한 구조를 사용했다.
데카르트와 페르마 모두 치료에 단일 축을 사용했으며 이 축을 기준으로 측정되는 가변 길이를 가지고 있습니다.한 쌍의 도끼를 사용하는 개념은 데카르트의 라 게오메트리가 1649년 프란스 반 슈텐과 그의 학생들에 의해 라틴어로 번역된 이후 나중에 도입되었다.이 해설자들은 데카르트의 [3]작품에 포함된 아이디어를 명확히 하기 위해 몇 가지 개념을 소개했습니다.
데카르트 좌표계의 발전은 아이작 뉴턴과 고트프리드 빌헬름 라이프니츠의 [4]미적분 개발에 근본적인 역할을 할 것이다.평면의 두 좌표 설명은 나중에 벡터 [5]공간의 개념으로 일반화되었다.
평면의 극좌표와 3차원 공간의 구면좌표와 원통좌표와 같은 많은 다른 좌표계가 데카르트 이후 개발되었다.
묘사
일차원
1차원 공간에 대한 데카르트 좌표계 선택(즉, 직선의 경우)은 선의 점 O(원점), 길이 단위 및 방향을 선택하는 것과 관련이 있습니다.방향은 O에 의해 결정되는 두 개의 반직선 중 어느 것이 양의 반이고 어느 것이 음의 반을 향해 "방향"(또는 "점")을 선택합니다.그런 다음 선의 각 점 P를 O로부터의 거리로 지정할 수 있으며, 어떤 반직선이 P를 포함하느냐에 따라 + 또는 - 기호를 사용합니다.
선택된 데카르트 시스템을 가진 선을 숫자 선이라고 합니다.모든 실수는 회선상의 고유한 위치를 가지고 있습니다.반대로, 선상의 모든 점은 실수와 같은 순서 있는 연속체의 숫자로 해석될 수 있습니다.
2차원
2차원의 데카르트 좌표계(사각형[6] 좌표계 또는 직교 좌표계라고도 함)는 수직선(축)의 순서쌍, 양쪽 축에 대한 단일 길이 단위 및 각 축에 대한 방향으로 정의됩니다.축이 만나는 지점은 두 개의 원점으로 간주되므로 각 축이 숫자 직선으로 바뀝니다.임의의 점 P에 대해서, 각 축에 수직인 P를 개입시켜 선을 긋고, 그 축과 만나는 위치를 수치로 해석한다.두 숫자는 선택된 순서대로 P의 데카르트 좌표이다.역구조를 사용하면 주어진 좌표에 따라 점 P를 결정할 수 있습니다.
첫 번째와 두 번째 좌표는 각각 Abscissa와 P의 좌표로 불리며, 축이 만나는 지점은 좌표계의 원점이라고 불립니다.좌표는 보통 (3, -10.5)와 같이 쉼표로 구분하여 괄호 안에 있는 두 개의 숫자로 작성됩니다.따라서 원점에는 좌표(0, 0)가 있고 원점에서 한 단위 떨어진 양의 반축에 있는 점에는 좌표(1, 0)와 (0, 1)가 있습니다.
수학, 물리학, 공학에서, 첫 번째 축은 보통 수평으로 정의되거나 묘사되고 오른쪽을 향하며, 두 번째 축은 수직이고 위쪽을 향합니다.(단, 일부 컴퓨터 그래픽스 컨텍스트에서는 좌표축이 아래쪽으로 향할 수 있습니다.)원점에는 종종 O라는 라벨이 붙고 두 개의 좌표는 종종 X와 Y 또는 x와 y라는 문자로 표시됩니다.X축과 Y축이라고 할 수 있습니다.알파벳의 뒷부분을 사용하여 알 수 없는 값을 나타내는 원래 규칙에서 문자를 선택할 수 있습니다.알파벳의 첫 부분은 알려진 값을 나타내기 위해 사용되었다.
선택된 데카르트 좌표계를 가진 유클리드 평면을 데카르트 평면이라고 한다.데카르트 평면에서 단위원(길이 단위와 반지름이 같고 원점에 중심이 있음), 단위 정사각형(대각선이 (0, 0) 및 (1, 1)에 끝점을 있음), 단위 쌍곡선 등과 같은 특정 기하학적 도형의 표준적 표현을 정의할 수 있습니다.
두 축은 사분면이라고 불리는 네 개의 직각으로 평면을 나눈다.사분면은 다양한 방법으로 이름이 붙거나 번호가 매겨질 수 있지만, 모든 좌표가 양수인 사분면을 보통 제1 사분면이라고 합니다.
점의 좌표가 (x, y)인 경우 X축과 Y축으로부터의 거리는 각각 y와 x입니다.여기서 ·는 숫자의 절대값을 나타냅니다.
3차원
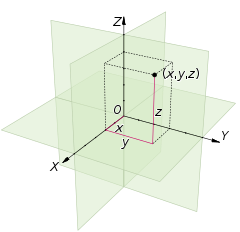
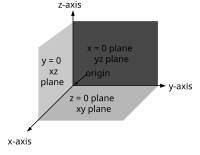
3차원 공간의 데카르트 좌표계는 공통점(원점)을 통과하고 쌍방향 수직, 각 축에 대한 방향 및 세 축 모두에 대한 단일 길이의 단위로 구성된 정렬된 세 개의 선(축)으로 구성됩니다.2차원의 경우와 마찬가지로 각 축은 숫자선이 된다.공간의 어떤 점 P에 대해서도 P를 통과하는 초평면을 각 좌표축에 수직이라고 간주하고, 그 초평면이 축을 절단하는 점을 숫자로 해석한다.P의 데카르트 좌표는 선택된 순서대로 세 개의 숫자이다.역구성은 세 개의 좌표가 주어진 점 P를 결정합니다.
혹은 점 P의 각 좌표를 대응하는 축의 방향에 의해 부호가 결정된 상태에서 다른 2개의 축에 의해 정의된 P에서 하이퍼플레인까지의 거리로 할 수 있다.
각 축 쌍은 좌표 하이퍼플레인을 정의합니다.이 초평면은 공간을 8개의 옥탄트로 나눈다.옥탄트는 다음과 같습니다.
좌표는 보통 (3, -2.5, 1) 또는 (t, u + v, θ/2)와 같이 괄호로 둘러싸인 세 개의 숫자(또는 대수식)로 작성됩니다.따라서 원점에는 좌표(0, 0, 0)가 있고 세 축의 단위점은 (1, 0, 0), (0, 1, 0) 및 (0, 0, 1)입니다.
세 축에는 좌표에 대한 표준 이름이 없습니다(단, abscissa, pordinate 및 applicate라는 용어가 사용되는 경우도 있습니다).좌표는 종종 X, Y 및 Z 또는 x, y 및 z 문자로 표시됩니다.X축, Y축, Z축이라고 할 수 있습니다.그러면 좌표 하이퍼플레인을 XY 평면, YZ 평면 및 XZ 평면이라고 할 수 있습니다.
수학, 물리학, 공학에서, 처음 두 축은 종종 수평으로 정의되거나 묘사되며, 세 번째 축은 위를 향한다.이 경우 세 번째 좌표는 높이 또는 고도라고 할 수 있다.방향은 보통 첫 번째 축에서 두 번째 축까지의 90도 각도가 점(0, 0, 1)에서 보았을 때 시계 반대 방향으로 보이도록 선택됩니다.이것은 일반적으로 오른손 법칙이라고 불립니다.

고차원
데카르트 좌표는 고유하고 비직렬하므로 데카르트 평면의 점은 실수의 쌍으로 식별할 수 있다. 즉, 데카르트 R × } = \ \ { 여기서 \ {R} \times \ { \mathbb이다.마찬가지로, 차원 n의 유클리드 공간에서의 점들은 n개의 실수의 튜플(목록), 즉 데카르트 n\displaystyle 을 사용하여 식별된다.
일반화
데카르트 좌표의 개념은 서로 수직이 아닌 축 및/또는 각 축을 따라 서로 다른 단위를 사용할 수 있도록 일반화합니다.이 경우, 각 좌표는 다른 축에 평행한 방향(또는 일반적으로 다른 모든 축에 의해 정의된 하이퍼플레인에 대해)을 따라 한 축에 투영함으로써 얻어진다.이러한 경사 좌표계에서 거리와 각도의 계산은 표준 데카르트계의 계산에서 수정되어야 하며, 많은 표준 공식(거리의 피타고라스 공식 등)은 유지되지 않는다(아핀 평면 참조).
표기법 및 표기법
점의 데카르트 좌표는 (10, 5) 또는 (3, 5, 7)과 같이 일반적으로 괄호로 쓰고 쉼표로 구분됩니다.원산지는 종종 대문자 O로 표기된다.해석기하학에서 미지의 좌표 또는 일반 좌표는 평면에서는 문자(x, y)와 3차원 공간에서는 문자(x, y, z)로 나타나는 경우가 많다.이 관습은 알 수 없는 값(많은 기하학적 문제에서 점의 좌표와 같은)에 대해 알파벳의 끝에 가까운 문자와 주어진 양에 대해 시작 근처에 있는 문자를 사용하는 대수학의 규칙에서 유래한다.
이러한 일반적인 이름은 물리나 엔지니어링과 같은 다른 영역에서도 종종 사용됩니다. 그러나 다른 문자는 사용될 수 있습니다.예를 들어 압력이 시간에 따라 어떻게 변화하는지를 보여주는 그래프에서는 그래프 좌표를 p 및 t로 표시할 수 있습니다.각 축은 보통 그것을 따라 측정되는 좌표의 이름을 따서 명명되므로 x축, y축, t축 등을 말합니다.
좌표명칭에 대한 또 다른 일반적인 규칙은 특히 n이 3보다 크거나 지정되지 않은 경우 n개의 좌표에 (x, x2, ..., xn)와1 같이 첨자를 사용하는 것입니다.일부 저자는 번호부여(x0, x1, ..., xn−1)를 선호합니다.이러한 표기법은 컴퓨터 프로그래밍에서 특히 유용합니다. 점의 좌표를 레코드 대신 배열로 저장함으로써 첨자가 좌표를 색인화하는 역할을 할 수 있습니다.
2차원 데카르트 시스템의 수학적 삽화에서, 첫 번째 좌표(전통적으로 아브시사라고 불림)는 왼쪽에서 오른쪽으로 수평 축을 따라 측정된다.그런 다음 두 번째 좌표(좌표)가 수직 축을 따라 측정되며, 일반적으로 아래쪽에서 위로 향합니다.데카르트 시스템을 배우는 어린 아이들은 일반적으로 2D 니모닉으로 시작하여 x축,[7] y축 및 z축 개념을 굳히기 전에 값을 읽는 순서를 배웁니다(예: '홀을 따라 걷다가 계단을 올라가면 x축을 따라 수직으로 올라갑니다).
그러나 컴퓨터 그래픽스 및 이미지 처리에서는 종종 컴퓨터 디스플레이에서 y축이 아래쪽을 향하도록 좌표계를 사용합니다.이 규칙은 1960년대(또는 그 이전)에 이미지가 원래 디스플레이 버퍼에 저장되는 방식에서 발전했습니다.
3차원 시스템의 경우 xy 평면을 수평으로 그리는 것이 관례이며, z축은 높이를 나타내기 위해 추가됩니다(양수 위).또, x축이 뷰어를 향하도록 오른쪽 또는 왼쪽으로 치우치는 규약이 있다.다이어그램(3D 투영 또는 2D 투시도)에 x축과 y축이 각각 수평 및 수직인 경우 z축이 뷰어 또는 카메라를 향해 "페이지 밖으로"를 가리키도록 표시되어야 합니다.이러한 3D 좌표계의 2D 다이어그램에서 z축은 추정 뷰어 또는 카메라 원근법에 따라 아래, 왼쪽 또는 아래 및 오른쪽을 가리키는 선 또는 광선으로 나타납니다.모든 다이어그램 또는 디스플레이에서 세 축의 방향은 전체적으로 임의입니다.단, 특별히 명기되어 있지 않는 한 서로 상대적인 축의 방향은 항상 오른쪽 규칙을 준수해야 합니다.물리학과 수학의 모든 법칙은 일관성을 보장하는 오른손잡이로 가정합니다.
3D 다이어그램의 경우 x와 y에 각각 "abscissa"와 "ordinate"라는 이름이 거의 사용되지 않습니다.이러한 경우 z 좌표를 적용이라고 부르기도 합니다.abscissa, pordinate 및 applicate라는 단어는 좌표 [6]값이 아닌 좌표 축을 가리키는 데 사용되기도 합니다.
사분원과 옥탄트
2차원 데카르트 시스템의 축은 평면을 [6]사분원이라고 불리는 네 개의 무한 영역으로 분할하고, 각각 두 개의 반축에 의해 경계됩니다.이것들은 종종 1번째부터 4번째까지 번호가 매겨지고 로마 숫자로 표시된다: I(좌표 둘 다 양의 부호가 있는 경우), II(좌표는 음수이고 좌표는 양수 +), III(좌표 둘 다 -), IV(좌표 둘 다 -)수학적 관습에 따라 축이 그려지면 번호는 오른쪽 상단("북동") 사분면에서 시계 반대 방향으로 이동합니다.
마찬가지로, 3차원 데카르트 시스템은 점의 좌표 부호에 따라 공간을 8개의 영역 또는 8진수로 [6]분할한다.특정 옥탄트의 이름을 붙이기 위해 사용되는 규칙은 부호(+ +) 또는 (- + -)를 나열하는 것입니다.임의의 수의 차원에 대한 사분면과 팔분면의 일반화는 오서트이며, 이와 유사한 명명 체계가 적용됩니다.
평면의 데카르트 공식
두 점 사이의 거리
데카르트 좌표(1, 1){및 ( ,y2) { (},2}})을 사용하는 평면의 두 점 사이의 유클리드 거리는 다음과 같습니다.
이것은 피타고라스의 정리의 데카르트 버전이다.3차원 공간에서 점, y, 1){}, 과 , 2, 2){ 사이의 거리는 다음과 같습니다.
피타고라스의 [8]정리를 두 번 연속으로 적용하면 얻을 수 있다.
유클리드 변환
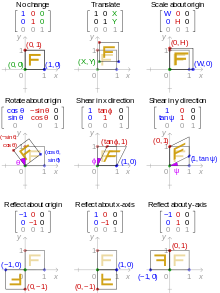
유클리드 변환 또는 유클리드 운동은 점들 사이의 거리를 보존하는 유클리드 평면의 점들의 (생략적인) 매핑이다.이러한 매핑에는 변환, 회전, 반사 및 활공 [9]반사의 네 가지 유형(등각도라고도 함)이 있습니다.
번역.
평면의 점 집합을 변환하여 그 사이의 거리와 방향을 보존하는 것은 집합의 모든 점의 데카르트 좌표에 고정된 숫자 쌍(a, b)을 추가하는 것과 같다.즉, 점의 원래 좌표가 (x, y)일 경우 변환 후 다음과 같이 됩니다.
회전
을 원점을 중심으로 시계 반대 방향으로 어느 정도 회전하려면{\(\는 모든 점을 좌표(x,y)로 좌표(x',y')로 치환하는 것과 같습니다.
다음과 같이 됩니다.
반사
(x, y)가 점의 데카르트 좌표인 경우, (-x, y)는 마치 선이 거울인 것처럼 두 번째 좌표축(y축)에 걸친 반사의 좌표입니다.마찬가지로, (x, -y)는 첫 번째 좌표축(x축)에 걸친 반사의 좌표입니다.보다 일반적으로 x축과 를 만드는 원점을 통과하는 선 전체에 걸친 반사는 모든 점을 좌표(x, y)로 치환하는 것과 같습니다.
다음과 같이 됩니다.
활공 반사
활공반사란 한 선에 걸친 반사에 이어 해당 선 방향으로의 변환이 이루어지는 것을 말합니다.이러한 조작의 순서는 문제가 되지 않는 것을 알 수 있습니다(번역을 먼저 하고 그 다음에 반영을 할 수 있습니다).
변환의 일반 매트릭스 형식
평면의 모든 아핀 변환은 행렬을 사용하여 균일한 방법으로 설명할 수 있습니다.이 목적을 위해 영역 좌표는 지점의{\displaystyle(x, y)}(), y)가 일반적으로 열 행렬()y).{\displaystyle{\begin{pmatrix}x\\y\end{pmatrix}}표시됩니다.}그 결과{\displaystyle(x, y)}는 다음 공식으로 주어진다. 지점(), y)에 상관 변환을 적용하는{\displaystyle(x',y의)}()′, y′).
아핀 변환 중에서, 유클리드 변환은 A(\A)가 직교한다는 사실에 의해 특징지어진다. 즉, 그 열은 유클리드 노름 1의 직교 벡터이거나, 또는 명시적으로,
이것은 A 곱하기 전치가 항등 행렬이라고 말하는 것과 같습니다.이러한 조건이 유지되지 않는 경우 공식은 보다 일반적인 아핀 변환을 나타냅니다.
변환은 A가 ID 매트릭스일 경우에만 변환입니다.변환은 A가 회전 행렬인 경우에만 특정 점을 중심으로 회전하는 것으로, A가 직교하고 있음을 의미합니다.
반사 또는 활공 반사는 다음과 같은 경우에 얻을 수 있다.
변환이 사용되지 않는 경우(, 1 2 }=}= 변환은 관련된 변환 행렬을 곱하는 것만으로 구성할 수 있습니다.일반적인 경우, 변환의 증강 행렬, 즉 변환 공식을 다시 쓰는 것이 유용합니다.
아핀 변환
유클리드 평면의 아핀 변환은 선을 선에 매핑하는 변환이지만 거리와 각도를 변경할 수 있습니다.앞 절에서 설명한 바와 같이, 이러한 행렬은 증강 행렬로 나타낼 수 있습니다.
유클리드 변환은 A (\의 2×2 행렬이 직교하는 아핀 변환입니다.
두 개의 아핀 변환의 구성을 나타내는 증강 행렬은 그들의 증강 행렬을 곱함으로써 얻어진다.
유클리드 변환이 아닌 일부 아핀 변환은 특정 이름을 받았습니다.
스케일링
스케일링에 의해 유클리드 이외의 아핀 변환의 예가 제시된다.그림을 크거나 작게 만드는 것은 모든 점의 데카르트 좌표에 같은 양의 숫자 m을 곱하는 것과 같다. 만약 (x, y)가 원래 그림 위의 점의 좌표라면 스케일링된 그림 위의 해당 점은 좌표를 갖는다.
m이 1보다 크면 수치가 커지고 m이 0과 1 사이이면 값이 작아집니다.
전단
전단 변환은 사각형의 상단을 옆으로 밀어 평행사변형을 형성합니다.수평 전단 기능은 다음과 같이 정의됩니다.
시어링은 수직으로 적용할 수도 있습니다.
오리엔테이션과 핸드니스
2차원
x축을 고정하거나 선택하면 y축이 방향까지 결정됩니다.즉, Y축은 반드시 X축에 0으로 표시된 점을 통해 X축에 수직이다.그러나 수직에 있는 두 개의 절반 선 중 어느 것을 양으로 지정하고 어느 것을 음으로 지정할지는 선택할 수 있습니다.이 두 가지 선택은 각각 데카르트 평면의 다른 방향(핸드니스라고도 함)을 결정합니다.
양의 x축이 오른쪽을 가리키고 양의 y축이 위쪽을 가리키고(그리고 x축이 "첫 번째"이고 y축이 "두 번째" 축) 평면의 일반적인 방향은 오른쪽 방향이라고도 하는 양의 방향 또는 표준 방향으로 간주됩니다.
정의 방향을 정의하기 위해 일반적으로 사용되는 니모닉은 오른쪽 규칙입니다.엄지손가락이 위로 향하도록 평면에 약간 닫힌 오른손을 놓고, 손가락이 x축에서 y축을 가리키도록 좌표계를 정방향 좌표계).
평면의 방향을 결정하는 다른 방법은 왼손의 법칙을 따르는 것입니다. 왼손은 엄지손가락을 위로 향하게 하여 평면에 놓습니다.
원점에서 축을 따라 양쪽으로 엄지손가락을 가리키는 경우, 손가락의 곡률은 해당 축을 따라 양의 회전을 나타냅니다.
평면 방향에 사용되는 규칙에 관계없이 좌표계를 회전하면 방향이 유지됩니다.한 축을 전환하면 방향이 반전되지만 둘 다 전환하면 방향이 변경되지 않습니다.
입체적으로
x축과 y축을 지정하면 z축이 놓여야 하는 선이 결정되지만 이 선에는 두 가지 방향이 있습니다.그 결과로 나타나는 두 가지 가능한 좌표계를 '오른손잡이'와 '왼손잡이'라고 한다.xy 평면이 수평이고 z축이 위쪽을 가리키고 xy 평면에서 x축과 y축이 양 방향의 2차원 좌표계를 형성하는 표준 방향을 오른손 방향 또는 양 방향이라고 합니다.
그 이름은 오른손 법칙에서 유래했다.오른손 검지가 앞으로 향하고 가운데 손가락이 안쪽으로 직각으로 구부러지며 엄지손가락이 양쪽으로 직각으로 배치되면 오른손 시스템에서 세 손가락은 x축, y축, z축의 상대적인 방향을 나타냅니다.엄지는 x축을, 검지는 y축을, 가운데 손가락은 z축을 나타냅니다.반대로 왼손으로 동일한 작업을 수행하면 왼손잡이 시스템이 생성됩니다.
그림 7은 좌측 및 우측 좌표계를 나타냅니다.2차원 화면에 3차원 물체가 표시되기 때문에 왜곡과 모호성이 발생합니다.아래(및 오른쪽)를 가리키는 축도 관찰자를 가리키는 반면, "중간" 축은 관찰자를 가리키는 것을 의미합니다.빨간색 원은 수평 xy 평면에 평행하며 x축에서 y축으로의 회전을 나타냅니다(두 경우 모두).따라서 빨간색 화살표가 Z축 앞을 통과합니다.
그림 8은 오른손잡이 좌표계를 묘사하기 위한 또 다른 시도이다.다시 3차원 좌표계를 평면에 투영함으로써 발생하는 애매함이 있다.많은 관찰자들은 그림 8을 볼록 입방체와 오목한 "코너" 사이의 "뒤집기"로 본다.이는 공간의 두 가지 가능한 방향에 해당합니다.도형을 볼록한 것으로 보는 것은 왼손잡이 좌표계를 제공한다.따라서 그림 8을 보는 "올바른" 방법은 x축이 관찰자를 가리키고 오목한 모서리를 본다고 상상하는 것이다.
표준 기준에서 벡터 표현
데카르트 좌표계의 공간상의 점은 좌표계의 원점에서 점을 [11]가리키는 화살표로 생각할 수 있는 위치 벡터에 의해서도 나타낼 수 있다.좌표가 공간적 위치(변위)를 나타내는 경우 원점에서 관심점까지의 벡터를 r로 나타내는 것이 일반적입니다. 2차원에서는 원점에서 점까지의 벡터는 데카르트 좌표(x, y)를 사용하여 다음과 같이 쓸 수 있습니다.
서 i ( 0 ){ } { { j ( 1){ { {는 일반적으로 X축 방향의 단위 벡터입니다.eas 이들은 버스터라고도 할 수 있다.)마찬가지로 3차원에서는 원점에서 데카르트 좌표 {이 있는 점까지의 벡터는 다음과 같이 [12]쓸 수 있습니다.
서 i ( 1 ), { {{ } \ \ \ \ \ \ \ \ \ { pmatrix , } () { \ { j .
모든 차원에 작용하는 다른 벡터를 얻기 위해 벡터를 곱하는 것에 대한 자연스러운 해석은 없지만, 그러한 곱셈을 제공하기 위해 복소수를 사용하는 방법이 있다.2차원 데카르트 평면에서 복소수 z = x + iy인 좌표(x, y)로 점을 식별합니다.여기서 i는 가상 단위이며 좌표(0, 1)를 갖는 점과 동일하기 때문에 x축 방향의 단위 벡터가 아니다.복소수를 곱하면 다른 복소수를 얻을 수 있기 때문에 이 식별은 벡터를 "다중"할 수 있는 수단을 제공합니다.3차원 데카르트 공간에서는 사분위수의 서브셋으로 동일한 식별이 가능하다.
적용들
데카르트 좌표는 실제 세계에서 가능한 많은 응용 프로그램을 가진 추상화입니다.단, 문제 어플리케이션 상의 좌표 중첩에는 세 가지 건설적인 단계가 포함됩니다.
- 거리 단위는 좌표로 사용되는 숫자로 표시되는 공간 크기를 정의해야 합니다.
- 특정 공간 위치 또는 랜드마크에 원점을 지정해야 합니다.
- 한 축을 제외한 모든 축에 대해 사용 가능한 방향 신호를 사용하여 축의 방향을 정의해야 합니다.
지구의 모든 점(즉, 지리 공간 3D)에 3D 데카르트 좌표를 겹치는 예로 고려해 보십시오.킬로미터의 원래 정의는 적도에서 북극까지의 표면 거리와 동일한 10,000 킬로미터의 지리 공간이었기 때문에 킬로미터는 좋은 단위 선택이다.대칭에 기초하여, 지구의 중력 중심은 원점의 자연스러운 위치를 암시합니다. 이것은 위성 궤도를 통해 감지될 수 있습니다.지구의 자전 축은 X, Y 및 Z 축에 대해 "위 vs. 아래"와 강하게 연관된 자연스러운 방향을 제공하므로 양의 Z는 지리 중심에서 북극으로 방향을 적용할 수 있습니다.X축을 정의하려면 적도의 위치가 필요하고, 본초 자오선은 기준 방향으로 두드러지기 때문에 X축은 지리 중심에서 경도 0도, 위도 0도로 방향을 잡습니다.X와 Z에 대해 고정된 3차원 및 2개의 수직 축 방향에서 Y축은 처음 두 가지 선택에 따라 결정됩니다.오른쪽 규칙을 따르려면 Y축이 지리 중심에서 경도 90도, 위도 0도를 가리켜야 합니다.경도 -73.985656도, 위도 40.748433도, 지구 반지름 40,000/2km에서 구면에서 데카르트 좌표로 변환하면 엠파이어 스테이트 빌딩의 지심 좌표를 추정할 수 있다. (x, y, z) = (1,330.53km, 4,635,4km)GPS 내비게이션은 이러한 지구중심 좌표에 의존합니다.
엔지니어링 프로젝트에서는 좌표 정의에 대한 합의가 중요한 기반입니다.새로운 응용을 위해 좌표가 미리 정의된다고 가정할 수 없기 때문에, 이전에는 그러한 좌표계가 없었던 곳에서 좌표계를 구축하는 방법에 대한 지식은 르네 데카르트의 사고를 적용하기 위해 필수적이다.
공간 애플리케이션은 모든 축을 따라 동일한 단위를 사용하는 반면, 비즈니스 및 과학 애플리케이션에서는 각 축에 관련된 측정 단위(kg, 초, 파운드 등)가 다를 수 있습니다.4차원 이상의 공간은 시각화하기 어렵지만, 데카르트 좌표의 대수는 비교적 쉽게 4개 이상의 변수로 확장될 수 있기 때문에 많은 변수와 관련된 특정 계산을 할 수 있다(이러한 종류의 대수적 확장은 고차원 공간의 기하학적 구조를 정의하는데 사용된다).반대로, 많은 비공간 변수 중 두 개 또는 세 개 사이의 대수적 관계를 시각화하기 위해 2차원 또는 3차원으로 데카르트 좌표의 기하학을 사용하는 것이 종종 도움이 됩니다.
함수 또는 관계의 그래프는 해당 함수 또는 관계를 충족하는 모든 점의 집합입니다.변수가 하나인 함수 f의 경우 모든 점 집합(x, y)입니다. 여기서 y = f(x)는 함수 f의 그래프입니다.두 변수의 함수 g의 경우 모든 점 집합(x, y, z)이며, 여기서 z = g(x, y)는 함수 g의 그래프입니다.그러한 함수 또는 관계의 그래프의 스케치는 함수 또는 관계의 모든 주요 부분으로 구성되며, 함수 또는 관계의 상대 극단, 오목부와 변곡점, 불연속점 및 최종 거동을 포함한다.이 모든 용어들은 미적분학에서 더 완전하게 정의된다.그러한 그래프는 함수나 관계의 본질과 행동을 이해하는 데 미적분학에서 유용하다.
「 」를 참조해 주세요.
레퍼런스
- ^ Bix, Robert A.; D'Souza, Harry J. "Analytic geometry". Encyclopædia Britannica. Retrieved 6 August 2017.
- ^ Kent, Alexander J.; Vujakovic, Peter (4 October 2017). The Routledge Handbook of Mapping and Cartography. Routledge. ISBN 9781317568216.
- ^ 버튼 2011, 페이지 374
- ^ 미적분 여행, 데이비드 베를린스키.
- ^ Axler, Sheldon (2015). Linear Algebra Done Right - Springer. Undergraduate Texts in Mathematics. p. 1. doi:10.1007/978-3-319-11080-6. ISBN 978-3-319-11079-0.
- ^ a b c d "Cartesian orthogonal coordinate system". Encyclopedia of Mathematics. Retrieved 6 August 2017.
- ^ "Charts and Graphs: Choosing the Right Format". www.mindtools.com. Retrieved 29 August 2017.
- ^ Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013). Calculus : Single and Multivariable (6 ed.). John wiley. ISBN 978-0470-88861-2.
- ^ 스마트 1998, 제2장
- ^ Brannan, Esplen & Gray 1998, 49페이지
- ^ Brannan, Esplen & Gray 1998, 부록 2, 페이지 377–382
- ^ David J. Griffiths (1999). Introduction to Electrodynamics. Prentice Hall. ISBN 978-0-13-805326-0.
원천
- Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998), Geometry, Cambridge: Cambridge University Press, ISBN 978-0-521-59787-6
- Burton, David M. (2011), The History of Mathematics/An Introduction (7th ed.), New York: McGraw-Hill, ISBN 978-0-07-338315-6
- Smart, James R. (1998), Modern Geometries (5th ed.), Pacific Grove: Brooks/Cole, ISBN 978-0-534-35188-5
추가 정보
- Descartes, René (2001). Discourse on Method, Optics, Geometry, and Meteorology. Translated by Paul J. Oscamp (Revised ed.). Indianapolis, IN: Hackett Publishing. ISBN 978-0-87220-567-3. OCLC 488633510.
- Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers (1st ed.). New York: McGraw-Hill. pp. 55–79. LCCN 59-14456. OCLC 19959906.
- Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. LCCN 55-10911.
- Moon P, Spencer DE (1988). "Rectangular Coordinates (x, y, z)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd, 3rd print ed.). New York: Springer-Verlag. pp. 9–11 (Table 1.01). ISBN 978-0-387-18430-2.
- Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. ISBN 978-0-07-043316-8. LCCN 52-11515.
- Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. LCCN 67-25285.













 모든 점을 좌표(x,y)로 좌표(x',y')로 치환하는 것과 같습니다.
모든 점을 좌표(x,y)로 좌표(x',y')로 치환하는 것과 같습니다.





 열
열 









 2×2 행렬이
2×2 행렬이 









 있는 점까지의 벡터는 다음과 같이
있는 점까지의 벡터는 다음과 같이 





