상대론적 도플러 효과

특수상대성이론
상대성 원리 상대성 이론
기초 관성 기준 프레임 빛의 속도 맥스웰 방정식 로렌츠 변환
결과들 시간 연장 길이 수축 상대론적 질량 질량-에너지 등가 동시성의 상대성 이론 상대론적 도플러 효과 토마스 세차 운동 상대론적 원반 벨의 우주선 역설 에렌페스트의 역설
시공간 민코프스키 시공간 시공간도 월드 라인 광원뿔
다이내믹스 적절한 시간 적정 질량 사모멘텀
역사 전구체 갈릴레오 상대성 이론 갈릴레오 변환 에테르 이론
사람 아인슈타인 솜메르펠트 미켈슨 몰리 피츠제럴드 헤르고츠 로렌츠 푸앵카레 민코프스키 피조 아브라함 태어난 플랑크 폰 라우에 에렌페스트 톨만 디락
대체 제제 특수 상대성 이론의 물리 포털 카테고리
v t

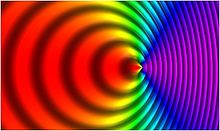
상대론적 도플러 효과는 특수 상대성이론에 의해 기술된 효과를 고려할 때 (고전 도플러 효과와 같이) 선원과 관찰자의 상대적인 움직임에 의해 발생하는 빛의 주파수(및 파장)의 변화이다.

상대론적 도플러 효과는 특수상대성이론의 시간확장효과를 포함하며 전파매체를 기준점으로 하지 않기 때문에 비상대론적 도플러 효과와는 다르다.이들은 관측된 주파수의 총 차이를 나타내며 필요한 로렌츠 대칭을 가지고 있습니다.

천문학자들은 세 가지 적색 편이/색조의 근원에 대해 알고 있습니다: 도플러 이동; 중력 적색 편이; 그리고 우주 팽창 (우주 자체가 늘어나는 곳)이 기사는 도플러 시프트에 대해서만 다루고 있다.

주요 결과 요약

다음 표에서는 β을 위해)v/c>0{\displaystyle \beta =v/c>0}수신기와 소스가 서로에게서 멀어져 가고 있다, v{\displaystyle v}이 상대 속도와 빛의{\displaystyle c}속도를 c, 그리고 γ=1/1− β 2{\textstyle \gamma =1/{\sqrt{1-\beta ^으로 추정된다.{2}}}}$$를 클릭합니다.

시나리오	공식	메모들
상대론적 종방향 도플러 효과	${\displaystyle {\fracda _{r}} = frac {f_{s}} {f_{r}} = frac {1+\flac} {1-\flac}}}}$
가로 도플러 효과, 기하학적 가장 가까운 접근법	${\displaystyle f_{r}=\display f_{s}$	블루시프트
가로 도플러 효과, 시각적으로 가장 가까운 접근법	${\displaystyle f_{r}=flac {f_{s}}{\display }}$	레드시프트
TDE, 원형 리시버 선원 주위의 움직임	${\displaystyle f_{r}=\display f_{s}$	블루시프트
TDE, 원형 소스 리시버 주위의 움직임	${\displaystyle f_{r}=flac {f_{s}}{\display }}$	레드시프트
TDE, 소스 및 수신기 주위에서 원을 그리며 공통 중심	${\displaystyle {f'}{f}=\leftfrac {1-R^{2}\off}{1-R'^{2}\Omega^{2}}\오른쪽)^{1/2}}$	도플러 시프트 없음 $R{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle {}^{}}$때(\$style$ R$=R'$ 표시)
임의의 방향으로의 움직임 리시버 프레임으로 측정됨	${\displaystyle f_{r}=f_{s}}{\display\left(1+\cos\theta_{r}\right)}}}$
임의의 방향으로의 움직임 소스 프레임으로 측정됨	$\displaystyle f_{r}=\display \left(1-\cos \theta _{s}\right)f_{s}$

파생

상대론적 세로 도플러 효과

소스와 리시버가 서로 직접 또는 서로 다른 방향으로 이동하는 종적 사례에 대한 상대론적 도플러 이동은 종종 고전적인 현상인 것처럼 유도되지만 시간 확장 ^[1][2]용어를 추가하여 수정된다.이것은 파인만이나^{[3] [4]}모린과 같은 1학년 물리학이나 역학 교과서에 적용된 접근법이다.

상대론적 세로 도플러 효과를 도출하기 위한 이 접근방식에 따라 수신기 또는 소스의 관찰자가 측정한 상대 $속도{\displaystyle }$ v${$ v$}$로 수신기와 소스가 서로 멀어지고 있다고 가정합니다(여기서 채택된 부호 규칙은 ${$ v$}$가 음수 i이다).수신기와 소스가 서로 향해 이동하고 있는 경우).

소스 참조 프레임의 문제를 검토합니다.

하나의 파면이 수신기에 도달했다고 가정합니다.다음 파장은 수신기에서 $\theta {\displaystyle {}_{}}$ ${\displaystyle s_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle c}$/ f ${\displaystyle s_{}}$ _ { $displaystyle$\ s $s$} =$c/f _$ { $s$} （ 여기서${\displaystyle {}_{}}{\displaystyle s_{}}$ s \ $display style$ \ s _ { $s$}는$$$$ 파장,${\displaystyle {}_{}}f{\displaystyle {}_{}}$ \ $displaystyle f_{s}$는 소스가 방출하는 파장의 주파수, c$style$ c$.$에드의 빛)

파장은 $속도{\displaystyle }$c(\$displaystyle$ c$,)$로 이동하지만 동시에 광파가 수신기에 충돌하는 $시간$ tr$,$ s(\$displaystyle t_{r,s$ ${\displaystyle {\mathrm{동안}}_{}}$ 수신기는 $속도{\displaystyle }$v(\$display$ v)로$$ 이동합니다.그렇게,

$여기$서 ${\displaystyle \beta }$ ${\displaystyle =}$v /$$ {$displaystyle$ \$displaystyle = v/c,}$는 빛의 속도에 따른 수신기의 속도입니다.$대응$하는 ${\displaystyle f_{}}$r ,$$s , ${\displaystyle s_{}}$ \ $display style f_{$r$,$$s}$ 。이것은, 송신원프레임내의 수신기에 파편이 영향을 주는 주파수입니다.

지금까지의 방정식은 정지된 선원과 움직이는 수신기를 가진 고전적인 도플러 효과의 방정식과 동일했다.

그러나 상대론적 효과로 인해 수신기의 클럭은 소스에서의 클럭에 대해 시간적으로 확장됩니다.t r $=$ ${\displaystyle t_{}}$r ,${\displaystyle {}_{}s}$ / ${\$ { $displaystyle$ t$_$ { r } = $\mathrm{t}$$$_ {$r$ , $s$} / \ displaystyle \ $\sqrt{{t\mathrm{}}^{}}$ _ r , s } / \ $tr$ , s $\}$ . lorentz $=$ 1$\sqrt{}$/ $2\sqrt{\mathrm{}}${ $textstyle =$1 / { textstyle = 1 / { 1 - rt { 1 - $rt$ { 1 - $rt$ { 1 - rt { 1 - rt { 1 - $\sqrt{{}^{}}$ { 1 - rt { 1$$-어느 시간이 연장되는지 알기 위해 ${\displaystyle {tr}_{}}$, s {\$displaystyle t_{r,$s$$}}는 소스가 정지되어 있는 프레임 내의 $시간임$을 상기합니다.수신기는 수신 주파수를 측정합니다.

1 1: $}{\displaystyle f_{r}=f_{r,s}\display}$ $=displaystyle = flac {1-\display ^{2}}}{\displayrt {1-\display ^{displayrt {1-\display }}}}}$ ${\displaystyle =displayrt {1-\display}{1+\display}},f_{s}.}$

비율

${\displaystyle {f_{s}}{f_{r}}={frac {1+\display}{1-\display}}}}$

(이 용어는 천체물리학의 주제에서 특히 널리 사용되고 있습니다: 상대론적 빛 참조).

대응하는 파장은 다음과 같습니다.

질문 2: ${\displaystyle {\fracda _{r}} = frac {f_{s}} {f_{r}} = frac {1+\fac} {1-\flac } }$

이동원을 가진 수신기의 기준 프레임에서 해석할 때 상대론적 도플러 시프트에 대한 동일한 식을 얻을 수 있다.이것은 상대성 원리의 기대와 일치하는데, 상대성 원리는 어떤 물체가 정지해 있는 것으로 간주되는지에 따라 결과가 달라질 수 없다는 것을 나타냅니다.이와는 대조적으로, 고전적인 비상대론적 도플러 효과는 ^[3][4]매체에 대해 고정된 소스인지 리시버인지에 따라 달라집니다.

가로 도플러 효과

선원과 수신기가 충돌하지 않는 경로를 따라 균일한 관성 운동으로 서로 접근한다고 가정합니다.가로 도플러 효과(TDE)는 (a) 이미터와 수신기가 가장 가까운 접근 지점에 있을 때 발생하는 특수 상대성 이론에 의해 예측되는 공칭 블루스시프트 또는 (b) 수신기가 이미터를 가장 가까운 ^[4]접근 지점에 있다고 볼 때 특수 상대성 이론에 의해 예측되는 공칭 적색 시프트를 참조할 수 있다.횡방향 도플러 효과는 특수 상대성 이론의 주요 새로운 예측 중 하나이다.

과학적 보고서에서 TDE가 레드시프트인지 블루시프트인지 여부는 관련된 실험 배열의 세부 사항에 따라 달라집니다.예를 들어, 1907년 아인슈타인의 TDE에 대한 원래 설명은 "캐널 광선" 빔(특정 종류의 가스 방전 튜브에 의해 생성되는 양이온 빔)의 중심(가장 가까운 점)을 보는 실험자를 묘사했다.특수상대성이론에 따르면 이동 이온의 방출 주파수는 로렌츠 인수에 의해 감소되어 수신 주파수는 동일한 ^{[p 1][note 1]}인자에 의해 감소(재변환)된다.

한편, 쿤디그(1963)는 뫼스바우어 흡수체가 중심 ^{[p 3]}뫼스바우어 방출체 주변의 빠른 원형 경로로 회전하는 실험을 설명했다.아래에 설명된 바와 같이, 이 실험적인 배열은 쿤디그의 블루스 시프트 측정으로 귀결되었다.

가까운 .

이 시나리오에서 가장 가까운 접근 포인트는 프레임에 의존하지 않으며 거리 대 시간에 변화가 없는 순간을 나타냅니다.그림 2는 이 시나리오를 쉽게 분석할 수 있는지가 ^[4]분석되는 프레임에 따라 다르다는 것을 보여줍니다.

• 에 있는 을 알 수 있습니다.리시버 프레임에서 시나리오를 분석하면 분석이 필요 이상으로 복잡하다는 것을 알 수 있습니다.천체의 겉으로 보이는 위치는 빛이 관찰자에게 도달하는 동안 물체의 움직임으로 인해 실제 위치(또는 기하학적 위치)에서 변위됩니다.선원은 리시버에 대해 시간 희석되지만, 이 시간 확장에 의해 암시되는 빨간색 시프트는 리시버와 선원의 외관 위치 사이의 상대적인 움직임의 세로 성분 때문에 블루시프트에 의해 상쇄됩니다.
• 림 소스.대신 소스 프레임에서 시나리오를 분석하면 훨씬 쉬워집니다.소스에 위치한 관찰자는 문제 진술을 통해 수신자가 자신과 가장 가까운 지점에 있음을 알 수 있습니다.리시버의가 있기 은 dr/= )에 (drdr)가 됩니다. 말하면 꿔꿔 in in in in in in in

문 3: $displaystyle f_{r}=\display f_{s}$

수신자는 소스가 가장 가까운 지점에 있다고 인식합니다.

이 시나리오는, 수신기가 소스의 패스에 대한 직각을 보는 것과 같습니다.이 시나리오의 분석은 수신기의 프레임에서 실시하는 것이 가장 좋습니다.그림 3은 소스가 ^[4]이동하더라도 소스가 수신기에 가장 가까웠을 때의 빛에 의해 수신기가 켜지는 것을 보여줍니다.광원의 클럭은 리시버 프레임에서 측정된 대로 시간이 연장되고, 광원의 움직임의 세로 구성요소가 없기 때문에 이 가장 가까운 지점에서 방출되는 광원의 빛은 주파수로 재시프트됩니다.

문 4: $f_{r}=flac {f_{s}}{\display }}$

문헌에서, 횡방향 도플러 이동에 대한 대부분의 보고서는 선원의 경로에 대한 직각으로 지시된 수신기의 관점에서 효과를 분석하며, 따라서 선원이 가장 가까운 지점에 있고 적색 편이를 관찰하는 것으로 본다.

주파수 늘 포인트

관성적으로 움직이는 소스와 리시버가 기하학적으로 서로 가장 가까운 접근에 있는 경우, 리시버는 블루시프트를 관찰하는 반면, 리시버가 소스를 가장 가까운 포인트로 보는 경우, 리시버는 레드시프트를 관찰하는 것이 분명합니다.빨간색 시프트그림 2에서 신호는 수신 경로에 수직으로 이동하며 블루시프트된다.그림 3에서 신호는 소스 경로에 수직으로 이동하고 적색 시프트된다.

그림 4와 같이 소스로부터 수신기까지 최단 거리를 이동하는 펄스에 대해 null 주파수 이동이 발생합니다.소스와 리시버의 속도가 같은 프레임에서 볼 때 이 펄스는 소스의 경로에 수직으로 방출되고 리시버의 경로에 수직으로 수신됩니다.펄스는 가장 가까운 지점보다 약간 먼저 방출되고, 약간 후에 ^[5]수신됩니다.

를 중심으로 을 그리며 .

그림 5는 이 시나리오의 두 가지 변형을 보여준다.두 변형 모두 단순한 시간 확장 ^[4]인수를 사용하여 분석할 수 있습니다.그림 5a는 기본적으로 그림 2b에 기재된 시나리오와 동등하며, 수신기는 소스로부터의 빛을$(\displaystyle$ \$gamma$의 계수에 의해 블루시프트되는 것으로 관찰합니다.그림 5b는 그림 3에 기재된 시나리오와 기본적으로 동등하며, 빛은 적색시프트됩니다.

유일하게 복잡해 보이는 것은 궤도를 도는 물체가 가속 운동을 하고 있다는 것이다.가속된 입자는 항상 정지된 관성 프레임을 가지고 있지 않다.그러나 입자와 순간적으로 결합하는 관성 프레임을 항상 찾을 수 있습니다.이 프레임은 순간 결합 기준 프레임(MCRF)으로 가속 입자의 분석에 특수 상대성을 적용할 수 있습니다.관성 관찰자가 가속하는 클럭을 보면 시간 ^[6]확장을 계산할 때 클럭의 순간 속도만 중요합니다.

그러나 그 반대는 사실이 아니다.두 물체가 가속된 움직임을 보이는 시나리오를 분석하려면 다소 더 정교한 분석이 필요합니다.이 점을 이해하지 못하는 것은 혼란과 오해를 불러일으켰다.

및 의 중심을 .

그림 6과 같이 선원과 리시버가 회전하는 로터의 반대쪽 끝에 있다고 가정해 보자. shouldshould （ shouldshould ） shouldshould （ shouldshould ） shouldshould （ ） shouldshould shouldshould shouldshould shouldshould shouldshould shouldshould shouldshould shouldshould shouldshould shouldshould shouldshould shouldshould shouldshouldshould shouldshould should should should should should should should should should should should should should should should should should should should should should should should should should should should should should should should should should should should 소스와 리시버 간에 도플러 이동이 없어야 합니다.

1961년 Champeney와 Moon은 정확히 이 시나리오에 대한 뫼스바우어 로터 실험을 실시했고 ^{[p 4]}뫼스바우어 흡수 과정이 회전의 영향을 받지 않는다는 것을 발견했다.그들은 그들의 발견이 특수상대성이론을 뒷받침한다고 결론지었다.

이 결론은 약간의 논란을 일으켰다.한 끈질긴 상대성 이론 비평가는 비록 실험이 일반 상대성 이론과 일치했지만, 특수 상대성 이론을 반박했다고 주장했는데, 그의 요점은 이미터와 흡수체가 균일한 상대 운동이었기 때문에 특수 상대성 이론이 도플러 변화를 관찰할 것을 요구했다는 것이다.이 비평가의 주장에 대한 오류는 늘 주파수 이동의 점에서 입증되었듯이 도플러 이동이 항상 균일한 상대 운동으로 ^[7]두 프레임 사이에서 관찰되어야 한다는 것은 사실이 아니라는 것이었다.또한 섹션 Source와 receiver가 가장 가까운 접근 지점에 있으므로 상대론적 시나리오 분석의 어려움은 종종 기준 프레임의 선택에 달려 있다.리시버 프레임에서 시나리오를 분석하려면 매우 지루한 대수가 필요합니다.실험실 ^[7]프레임에서 이미터와 흡수체 사이의 도플러 이동이 없음을 확인하는 것은 훨씬 쉽고, 거의 사소한 일입니다.

그러나 실제로 챔피니와 문 후보의 실험은 특수상대성이론에 대해 찬반 양론이 없었다.설정의 대칭성 때문에, 실질적으로 생각할 수 있는 모든 도플러 이론이 균일한 관성 운동에서 프레임 사이의 도플러 이동에 대해 이 실험에서 ^[7]null 결과를 도출해야 한다는 것이 밝혀졌습니다.

중심에서 등거리에 있지 않고 방사체와 흡수체가 로터의 중심에서 다른 거리에 있다고 가정합니다.로터상의 임의의 위치에 있는 $Rµ$의 이미터 및 $반경{\displaystyle }$R의 $흡수체$({displaystyle$$ R$})$의 경우 $이미터{\displaystyle {}^{}}$ 주파수 fθ$,$ {$displaystyle$ f$',$ 및$$ 흡수체 $주파수{\displaystyle }$ f$,$ {$displaystyle$ f$}$의 비율은 다음과 같습니다.

문 5: ${f'}{f =\leftfrac {1-R^{2}\off}{^2}$

여기서$\delta {\displaystyle }$(\$displaystyle \omega)$는 로터의 각 속도입니다.소스와 이미터는 180° 떨어져 있을 필요는 없지만 ^{[p 5][8]}중심에 대해 임의의 각도로 배치할 수 있습니다.

의

상대론적 세로형 도플러 효과에 사용된 분석은 소스와 리시버의 관성 운동이 지정된 ^[2][9]각도에 있을 경우 도플러 시프트를 계산하기 위해 간단한 방식으로 확장될 수 있다.그림 7은 수신기의 프레임에서 측정된 ${\displaystyle {각도\theta }_{}}$ r ${\$ _${r}$에서 속도$v{\displaystyle }$ {\$displaystyle$ v$}$로 이동하는 선원의 시나리오를 나타낸다.시선 방향에 따른 소스 움직임의 반경 구성요소는 ${\displaystyle v}$ cos ${\displaystyle {}_{}{r}_{}}$. { $displaystyle$v \$cos$ {$r$} 입니다.$}$

아래 방정식은 로렌츠 인자에 의해 수정된 정지 및 이동 소스에 대한 고전적인 도플러 시프트로 해석할 수 있습니다${\displaystyle .}\delta {\displaystyle }$ : \ $displaystyle$\$gamma$ :$$}

문 6: ${\displaystyle f_{r}=f_{s}}{\display \left(1+\cos \theta _{r}\right}}}.}$

${\displaystyle {\theta }_{}}$ r ${\displaystyle {}_{}}$ ${\displaystyle {90}^{}}$ ${\$ { $displaystyle \theta$_ {r } =$90^{\display$ $\}\}$일 경우, 다음과 같이 횡방향 도플러 효과를 얻을 수 있다.

$displaystyle f_{r}=f_{s}}{\display}},$

아인슈타인은 1905년 특수상대성이론에 ^{[p 2]}관한 논문에서 도플러 이동 방정식에 대해 다소 다른 외관 방정식을 얻었다.아인슈타인 방정식의 변수 이름을 여기서 사용되는 변수 이름과 일치하도록 바꾼 후, 그의 방정식은 다음과 같습니다.

문 7: $\displaystyle f_{r}=\cos \left(1-\cos \theta _{s}\right)f_{s}.}$

차이점은 아인슈타인이 리시버 레스트 프레임이 아닌 소스 레스트 프레임에 대해 각도 $(\$ _${s})$를 평가했다는 사실에서 비롯된다.$§$ \ $displaystyle$ \$theta _{$s$$}는 상대론적 수차의 영향으로 ${\displaystyle {인해}_{}}$ $§$ r \$displaystyle$ \$theta _{$r$$}과(와) 같지 ${\displaystyle {\mathrm{않습니다}}_{}}$.상대론적 수차 방정식은 다음과 같다.

문 8: $\ fracdisplaystyle \ \theta _{r}=param frac {1-\cos \theta _{s}}}},}$

상대론적 수차 방정식 8을 방정식 6으로 대체하면 도플러 이동에 ^[9]대한 이러한 대체 방정식의 일관성을 보여주는 방정식 7이 생성됩니다.

방정식 6에서 ${\displaystyle {\theta }_{}}$ r $=$(\$displaystyle \theta$ _${r$}=$0)$ 또는$$ 등식 7에서 ${\displaystyle {\theta }_{}}$ s $=$(\$displaystyle \theta$ _${s$}=$0)$을 설정하면 상대론적 세로 도플러 시프트 식인 방정식 1이 생성됩니다.

이러한 결과를 도출하기 위한 4가지 벡터 접근방식은 Landau 및 Lifshitz(2005)^[10]에서 찾을 수 있다.

★★★★★

그림 8은 상대론적 도플러 효과와 상대론적 수차가 비상대론적 도플러 효과와 빛의 비상대론적 수차와 어떻게 다른지를 대략적인 질적 의미에서 이해하는 데 도움을 준다.관측자가 570 nm의 단색 빛을 방출하는 노란색 별에 의해 모든 방향으로 균일하게 둘러싸여 있다고 가정합니다.각 다이어그램의 화살표는 주변 환경에 대한 관측자의 속도 벡터를 0.89c로 나타냅니다.

• 상대론적 경우 원자외선에서는 관측자 앞의 빛이 137nm 파장으로 블루시프트되고, 단파장 적외선에서는 관측자 뒤의 빛이 2400nm로 적시프트된다.빛의 상대론적 수차로 인해 관측자에 대한 직각의 물체는 앞으로 63° 이동된 것으로 보인다.
• 비상대론적 경우 관찰자 앞의 빛은 중자외선에서는 300nm 파장으로, 관찰자 뒤의 빛은 중간적외선에서는 5200nm로 적시프트된다.빛의 수차로 인해 이전에 관측자에 대한 직각의 물체는 전방으로 42° 이동된 것으로 보인다.
• 두 경우 모두 관측자의 앞과 뒤에 있는 단색 별은 보이지 않는 파장으로 도플러 시프트됩니다.그러나 만약 관찰자가 자외선과 적외선을 볼 수 있는 눈을 가졌다면, 그는 앞의 별들이 뒤에 있는 별들보다 더 밝고 가깝게 뭉쳐 있는 것을 보겠지만, 별들은 훨씬 더 밝고 상대론적 ^[11]경우 훨씬 더 집중되어 있을 것이다.

실제 별은 단색이 아니라 흑체 분포에 가까운 파장을 방출합니다.관측자 앞의 별들이 더 푸르스름한 색을 보인다는 것은 반드시 사실이 아니다.이는 전체 스펙트럼 에너지 분포가 이동하기 때문이다.가시광선을 눈에 보이지 않는 자외선 파장으로 블루쉬프트함과 동시에 적외선을 블루쉬프트하여 가시 범위로 한다.정확히 어떤 색의 변화가 보이는지는 인간의 눈의 생리와 ^[12][13]관찰되는 광원의 스펙트럼 특성에 따라 달라진다.

에 대한

이 도플러 효과도 인지된 소스 강도를 수정하는:invariant[p6][주 2]이것은 총 방사 강도(가산에 모든 주파수)은 D의 4을 곱한 있음을 암시한다. 이 간결하게 사실은 소스 강도는 주파수의 입방체로 하는 로렌츠로 표현할 수 있(임의의 방향을)인자oppler빈도를 지정합니다.

그 결과, 플랑크의 법칙은 흑체 ${\displaystyle \frac{{복사}^{}}{}}$를 ${\displaystyle \frac{{f\frac{}{}}^{}}{}}$ ${\displaystyle \frac{{\frac{}{}}^{}}{}}$ e h k${\displaystyle \frac{{\frac{}{}}^{}{\frac{T}{}}^{}}{}}$ - ${\displaystyle \frac{1}{}}$({$displaystyle {f^{3}}{e^{\frac {hf}{k$})에 비례하는 스펙트럼 강도를 갖는 것으로 기술하고 있다.$T}-1}}($$여기$서 T ${\displaystyle$ T$}$는 소스 온도이고 f$${\$displaystyle$ f$}$ 주파수는$$ f {\displaystyle f}) 도플러 시프트를 통해 보이는 흑체 스펙트럼은 여전히 주파수와 동일한 온도에 곱한 흑체 스펙트럼이라는 결론을 도출할 수 있다.

이 결과는 빅뱅 이론을 우주론적 ^[14]적색편이를 설명하기 위해 제안된 대안 이론과 구별하는 데 도움이 되는 증거 중 하나를 제공한다.

★★★★

횡방향 도플러 효과가 특수 상대성 이론의 주요 새로운 예측 중 하나이기 때문에, 이 효과의 검출과 정확한 정량화는 특수 상대성 이론을 검증하려는 실험의 중요한 목표가 되어 왔다.

아이브스 스틸웰

아인슈타인(1907)은 처음에 TDE가 ^{[p 1]}빔에 대해 직각으로 "캐널 광선"을 관찰함으로써 측정될 수 있다고 제안했다.당시 이용 가능한 입자 빔의 최대 속도는 광속의 수천분의 몇에 불과했기 때문에 이 방식에 따라 TDE를 측정하려는 시도는 실용적이지 않다는 것이 입증되었습니다.

그림 9는 운하 광선 빔(H1+, H2+ 및 H3+ 이온의 혼합물)이 운하 광선을 채우는 데 사용되는 희박한 수소 가스에서 제거된 전자와 재결합할 때 방출되는 4861 앙스트롬 라인을 측정하려고 시도한 결과를 보여줍니다.TDE 4861.06입니다.왼쪽에서 세로 방향 도플러 이동은 TDE를 관찰할 수 없을 정도로 방출선을 넓히는 결과를 초래한다.중간 수치는 시야를 빔의 정확한 중심으로 좁혀도 빔의 정확한 직각으로부터의 매우 작은 편차는 예측된 효과에 필적하는 변화를 가져온다는 것을 보여줍니다.

Ives와 Stilwell(1938)은 TDE의 직접 측정을 시도하는 대신 거의 세로 방향의 직접 빔(파란색)과 반사 이미지(빨간색)를 동시에 관찰할 수 있는 오목 거울을 사용했습니다.분광학적으로 세 개의 선이 관찰된다.배치되지 않은 방출선, 블루시프트 및 레드시프트 라인.빨간색 시프트 라인과 파란색 시프트 라인의 평균은 배치되지 않은 방출 라인의 파장과 비교됩니다.Ives와 Stilwell이 측정한 차이는 실험 한계 내에서 특수 상대성이론에 ^{[p 7]}의해 예측된 효과와 일치했다.

이후 Ives와 Stilwell 실험의 다양한 반복은 블루시프트 및 레드시프트 입자 빔 방출의 평균을 측정하기 위한 다른 전략을 채택했다.최근 몇 번의 실험 반복에서는 두 개의 역회전 입자 빔을 관측하기 위해 현대적인 가속기 기술이 사용되었습니다.다른 반복에서는 빠르게 이동하는 입자 빔에 의해 방출되는 감마선의 에너지가 입자 빔의 방향에 대해 반대 각도로 측정되었다.이러한 실험들은 실제로 입자 빔의 파장을 빔과 직각으로 측정하는 것이 아니기 때문에, 일부 저자들은 그들이 측정하는 효과를 TDE가 ^{[p 8][p 9]}아닌 "4차 도플러 이동"이라고 부르는 것을 선호해 왔다.

입자 가속기 기술의 등장으로 Ives와 Stilwell이 사용할 수 있었던 것보다 상당히 높은 에너지를 가진 입자 빔의 생산이 가능해졌습니다.이를 통해 아인슈타인이 원래 상상했던 방법에 따라, 즉 90° 각도로 입자 빔을 직접 보는 방식으로 횡방향 도플러 효과의 시험을 설계할 수 있었다.예를 들어, Hasselkamp 외 연구진(1979)은 2.53×10cm⁸/s에서 9.28×10cm⁸/s까지의 속도로 이동하는 수소 원자에 의해 방출되는 Hα 라인을 관찰했고, 상대론적 근사치의 2차 항의 계수는 0.52±^{[p 10]}0.03으로 이론값 1/2과 매우 일치한다는 것을 발견했다.

회전 플랫폼에 대한 TDE의 다른 직접 테스트는 핵 감마선 방출 및 ^[15]흡수를 위한 매우 좁은 공진 라인을 생산할 수 있는 뫼스바우어 효과의 발견으로 가능했다.뫼스바우어 효과 실험은 약 2×10cm⁴/s의 이미터 흡수체 상대 속도를 사용하여 TDE를 쉽게 검출할 수 있음을 입증했다.이러한 실험에는 Hay 등(1960),^{[p 11]} Champeney 등(1965),^{[p 12]} 쿤디그(1963)^{[p 3]}가 수행한 실험이 포함된다.

( )

가로 도플러 효과와 특수 상대성 이론의 운동학적 시간 확장은 밀접하게 관련되어 있다.TDE의 모든 검증은 키네마틱 시간 확장에 대한 검증을 나타내며, 대부분의 키네마틱 시간 확장에 대한 검증은 TDE에 대한 검증을 나타내기도 한다. 온라인 리소스 "특수 상대성의 실험적인 근거는 무엇인가?"는 수년간 특수 상대성 ^[16]이론의 다양한 측면을 검증하는 데 사용된 많은 테스트를 간단한 논평과 함께 문서화했다.카이볼라 외 연구진(1985)^{[p 13]}과 맥고완 외 연구진(1993)^{[p 14]}은 이 자원에서 시간 연장 실험으로 분류된 실험의 예이다.이 2개는 TDE 테스트이기도 합니다.이 실험들은 두 개의 레이저의 주파수를 비교했는데, 하나는 빠른 빔에서 네온 원자의 전이 주파수에 고정되었고, 다른 하나는 열 네온에서 같은 전이에 고정되었다.1993년 버전의 실험은 시간 연장을 검증했고, 따라서 TDE는 2.3×10의⁻⁶ 정확도로 검증했다.

와

1학년 물리학 교과서는 거의 예외 없이 뉴턴 운동학의 관점에서 소리를 위한 도플러 이동을 분석하고 상대론적 운동학의 관점에서 빛과 전자기 현상을 위한 도플러 이동을 분석합니다.을 사용하다

소리에 대한 도플러 효과의 전통적인 분석은 정확하고 상대적인 분석에 대한 느린 근사치를 나타냅니다.소리의 완전 상대론적 분석은 사실 소리와 전자기 현상 모두에 동일하게 적용된다.

그림 10의 시공간도를 살펴본다.이 다이어그램에는 음차(소스)와 수신기의 월드 라인이 모두 표시되어 있습니다.이벤트 O와 A는 음차의 두 가지 진동을 나타냅니다.포크의 주기는 OA의 크기이며 AB의 역 기울기는 이벤트 B에 대한 신호 전파 속도(즉, 음속)를 나타냅니다.따라서 다음과 같이 ^[9]쓸 수 있습니다.

${\displaystyle c_{}}$ s ${\displaystyle {}_{}}$ ${\displaystyle \frac{x_{}}{}}$B - ${\displaystyle \frac{x_{}}{}}$ A ${\displaystyle \frac{t_{}}{}}$B - ${\displaystyle \frac{t_{}}{}}$A { $displaystyle$ c$_$ { s } =$flac${ x$_$ { B$}$ - x$_$ { A } } { $t$_ { B } - t$_$ { $A$} $$（ 음속)

$=$$A}}{t_{A}}}:$ ${\displaystyle v_{}}$ r $=$ ${\displaystyle x\frac{{}_{}}{}}$ ${\displaystyle \frac{B_{}}{}}$ ${\displaystyle \frac{{}_{}}{{}_{}}}$ {\ $displaystyle v_{r$}= $scfrac {x_{B}}{t_{B}}}}$ (소스 및 리시버)

$=OA {{\displaystyle OA = displayrt {t_{A}^2}-(x_{A}/c)^2}}}$

$OB =B}/displaystyle OB = sqtrt {t_{B}^2}-(x_{B}/c)^2}})$

${\displaystyle v_{}}$ s$$\ $displaystyle v_{s}$ 및 $v$ r$$\ $displaystyle v_{r}$는 ${\displaystyle {cs}_{}}$ ${\displaystyle {}_{}}${\ $displaystyle c_{s}$보다 작은 것으로 간주됩니다.그렇지 않으면 매체를 통과하는 것이 충격파를 설정해 계산을 무효화하기 때문입니다.일부 루틴 대수는 주파수 비율을 제공합니다.

문 9: $displaystyle {f_{r}}{f_{s}}={OA}{OB}}}$ $= = specfrac {displaystyle = {1-{}}{c}}}{c}}}{c}}}}}{\1-{1-{c}}}}}}}}}}}$

${\displaystyle v_{}}$ r$${ $displaystyle$ v$_$ { $r$} $v$ ${\displaystyle {vv}_{}}$ s$${ $displaystyle$ v$_$ { $s$}이$$ c$${ $displaystyle$ c$$}에 비해 작은 경우 $위$의 방정식은 소리용 도플러 공식으로 축소됩니다.

신호 $전파{\displaystyle {}_{}}$ 속도 ${$가$$c{$displaystyle$ c$\}$에 $근접$하면 소스와 수신기의 절대 $속도{\displaystyle {}_{}}$ ${\displaystyle v_{}}${$displaystyle$ $v_{s$$}$ $및$ ${$가 고정 매체에 관계없이 단일 상대 속도로 병합됨을 알 수 있습니다.실제로 우리는 상대론적 세로 도플러 ^[9]이동 공식인 방정식 1을 얻습니다.

그림 10의 시공간 다이어그램 분석은 선원과 수신기가 시선(즉, 공선 운동)을 따라 직접 이동하는 일반적인 공식을 제공했다.

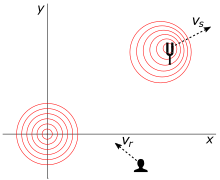
그림 11은 2차원의 시나리오를 보여준다.소스는 속도 $($ 시)로 이동한다.\displaystyle$\mathbf {v_{s}} }$ $$。수신 시 $속도{\displaystyle {\mathbf{}}_{}}$$$${\displaystyle {v\mathbf{}}_{}}$ r$$r r r r \ displaystyle \ $mathbf$$${ $v$$_$ r }$}$로 이동하는 수신기를 향해 C {\ $displaystyle \ mathbf$ {$C$$} }$ $속도$로 이동하는 신호를 방출합니다.분석은 신호 ${\displaystyle 속도\mathbf{}}$ C$displaystyle \mathbf {C} })$가 ^[5]방향과 무관한 좌표계에서 수행됩니다.

의 적정 은, 「소스와 의 주파수는 '비'입니다.

문 10: ${{\ { _ {C,}}}}}}}}}){1- {{\s(\theta _ {C,v_{r}}}}}}}}}}{1-{\frac {{\f}}$

선행비는 고전적인 도플러 효과의 형태를 가지고 있는 반면, 제곱근 항은 상대론적 보정을 나타냅니다.소스 프레임에 상대적인 각도를 고려하면 ${\displaystyle v_{}}$ s $=$ $(\displaystyle v_{s$}=$0)$이고 방정식은 도플러 효과에 대한 아인슈타인의 1905년 공식인 방정식 7로 줄어든다.수신기의 프레임에 상대적인 각도를 고려하면 ${\displaystyle v_{}}$ r $=$ $(\displaystyle v_{r$}=$0)$이며 방정식은 앞에서 ^[5]설명한 도플러 이동 방정식의 대체 형태인 식 6으로 감소한다.

「 」를 참조해 주세요.

• 도플러 효과
• 도플러 전송
• 레드시프트
• 블루시프트
• 시간 연장
• 중력 시간 확장
• 특수상대성이론

메모들

주요 소스

레퍼런스

추가 정보

• Moriconi, M (1 November 2006). "Special theory of relativity through the Doppler effect". European Journal of Physics. 27 (6): 1409–1423. arXiv:physics/0605204. Bibcode:2006EJPh...27.1409M. doi:10.1088/0143-0807/27/6/015. S2CID 11347287.

외부 링크

• 상대론적 도플러 효과를 보여주는 워프 특수 상대성 시뮬레이터 컴퓨터 프로그램.
• Kraus, Ute; Zahn, Corvin. "Space Time Travel: Visualization of the theory of relativity". SpacetimeTravel.org. Physics and Astronomy Education Group, Hildesheim University, Germany. Retrieved 17 October 2018.