위치(지오메트리)

Radius 벡터

{\vec {r}}

→

{\

은

(

는) 원점 O에 대한

\mathrm {P} (x,y,z)

점

P(x

y

,

z

)의 위치를 나타낸다

{\vec {r}}

.

데카르트 좌표계

{\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

→

{\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

=

{\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

{\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

{\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

{\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

+

{\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

{\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

+ z

{\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

{\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

{\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

{\

z

{\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

기하학에서 위치 벡터 또는 반지름 벡터라고도 하는 위치 또는 위치 벡터는 임의의 기준 원점 O와 관련하여 공간에서 점 P의 위치를 나타내는 유클리드 벡터다. 일반적으로 x, r 또는 s로 표시되며, O에서 P까지의 직선 세그먼트에 해당한다. 즉, 기원을 P:^[1]에 매핑하는 것은 변위 또는 번역이다.

\mathbf {r} ={\overrightarrow {OP}}

위치 벡터(position vector)라는 용어는 주로 미분 기하학, 역학, 때로는 벡터 미적분학 분야에서 사용된다.

흔히 이것은 2차원 공간이나 3차원 공간에서 사용되지만 유클리드 공간에는 쉽게 일반화될 수 있고 어떤 차원의 공간에도 붙일 수 있다.^[2]

정의

삼차원

공간 곡선(3D) 위치 벡터는 스칼라 t에 의해 파라미터로 지정된다. r = 빨간색 선은 곡선과 접선이고 파란색 평면은 곡선과 정규적이다.

3차원에서는 3차원 좌표 세트와 그에 상응하는 기본 벡터를 사용해 한 점의 공간 위치를 정의할 수 있다. 그 중 어느 것이든 당면한 과제에 가장 간단한 것이 사용될 수 있다.

일반적으로 익숙한 데카르트 좌표계 또는 때로는 구형 극좌표 또는 원통형 좌표를 사용한다.

{\displaystyle{\begin{정렬}\mathbf{r}(t)&, \equiv};\equiv(r,\theta ,\phi)\equiv r(t)\mathbf{\hat{e}}_{r}{\big(}\theta(t),\phi(t){\big)}\\&{r}\mathbf, \equiv}(r,\theta ,z)\equiv r(t)\mathbf{\hat{e}{r}\mathbf_{(x,y,z)\equiv x(t)\mathbf{\hat{e}_ᆷ+y(t)\mathbf{\hat{e}}_ᆹ+z(t)\mathbf{\hat{e}}_{z}\\&{r}\mathbf.r}{\big(}\t헤타(t){\big )}+z(t)\mathbf {\hat {e} _{z}\\\end{aigned}}}}

여기서 t는 직사각형 또는 원형 대칭으로 인해 매개변수다. 이러한 서로 다른 좌표와 해당 기본 벡터는 동일한 위치 벡터를 나타낸다. 보다 일반적인 곡선 좌표를 대신 사용할 수 있으며 연속체 역학과 일반 상대성 같은 맥락에 있다(후자의 경우 추가 시간 좌표가 필요하다).

n 치수

선형대수는 n차원 위치 벡터의 추상화를 허용한다. 위치 벡터는 기본 벡터의 선형 조합으로 표현될 수 있다.^[3]^[4]

\mathbf {r} =\sum _{i=1}^{n}x_{i}\mathbf {e} _{i}=x_{1}\mathbf {e} _{1}+x_{2}}\mathbf {e} _{2}+\mathb +x_{n}\mathbf {e} _{n}.

모든 위치 벡터 세트는 위치 공간(위치가 위치 벡터인 벡터 공간)을 형성하는데, 그 이유는 위치 추가(벡터 추가) 및 길이 축척(scalar 곱셈)이 가능하기 때문이다. "공간"의 개념은 직관적이다. 각 x_i(i = 1, 2, n)는 어떤 값도 가질 수 있기 때문에, 값의 집합은 공간의 점을 정의한다.

위치 공간의 치수는 n이다(dim(R) = n로도 표시됨). 기본 벡터 e에_i 대한 벡터 r의 좌표는 x이다_i. 좌표 벡터는 좌표 벡터 또는 n-투플(x₁, x₂, x, …, x_n)을 형성한다.

각 좌표 x는_i 다수의 매개변수 t로 매개변수화할 수 있다. 하나의 매개변수 x_i(t)는 곡선 1D 경로를, 두 매개변수_i x₁(t₂, t)는 곡선 2D 표면을, 세 개의_i x(t₁, t₂₃, t)는 곡선 3D 공간을 설명한다.

기본 집합 B = {e₁, e₂, …, e_n}의 선형 스팬은 위치 공간 R, 표시된 스팬(B) = R과 동일하다.

적용들

미분 기하학

위치 벡터 필드는 연속적이고 가변적인 공간 곡선을 설명하기 위해 사용된다. 이 경우 독립 매개변수는 시간이 아니라 곡선의 호 길이일 수 있다.

역학

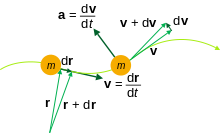
어떤 움직임의 방정식에서, 위치 벡터 r(t)은 이 함수가 입자(즉, 점 질량)의 움직임 - 어떤 시간 t에서 주어진 좌표계에 상대적인 위치를 정의하기 때문에 일반적으로 가장 추구하는 수량이다.

위치의 측면에서 움직임을 정의하기 위해, 각 좌표는 시간에 따라 파라메트리될 수 있다. 각 연속적인 시간의 값은 좌표에 의해 주어진 연속적인 공간 위치의 순서에 해당하기 때문에, 연속적인 많은 위치의 연속적인 한계는 입자 트레이스의 경로다.

1차원의 경우 그 위치는 한 가지 요소만 가지고 있어 효과적으로 스칼라 좌표로 퇴보한다. 예를 들어 X 방향의 벡터 또는 방사형 r 방향일 수 있다. 등가 공명은 다음을 포함한다.

\displaystyle \mathbf {x} \equiv x(t),\cHB r(t),\cHB s\equiv s(t)}

포지션 파생상품

고전 입자의 운동학적 수량: 질량 m, 위치 r, 속도 v, 가속도 a

시간 t의 함수인 위치 벡터 r의 경우 시간 파생상품은 t에 대해 계산할 수 있다. 이러한 파생상품은 운동학, 제어 이론, 공학 및 기타 과학 연구에 공통의 효용을 가진다.

속도: $\mathbf {v} ={\frac {\mathrm {d} \mathbf {r}{\mathrm {d} t},$

여기서 dr은 무한히 작은 변위(vectorvector)이다.

가속: $\mathbf {a} ={\frac {\mathrm {d} {v}{\mathbf {d} t}={\frac {\mathrm {d} ^{2}\mathbf {r}{d}}}{\mathbrmatr} t^{2}}.$

얼간이: $\mathbf {j} ={\frac {\mathrm {d} \mathbf {a} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {v} }{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}\mathbf {r} }{\mathrm {d} t^{3}}}.$

위치의 첫 번째, 두 번째, 세 번째 파생상품에 대한 이러한 명칭은 기본 운동학에서 일반적으로 사용된다.^[5] 더 나아가 고차파생상품도 비슷한 방식으로 계산할 수 있다. 이러한 고차 파생상품에 대한 연구는 원래 변위함수의 근사치를 개선할 수 있다. 변위 함수를 무한 시퀀스의 합으로 정확하게 나타내기 위해서는 이러한 고차 항이 필요하며, 공학과 물리학의 여러 해석 기법이 가능하다.

참고 항목

메모들

^ 변위라는 용어는 주로 기계학에서 사용되는 반면, 번역은 기하학에서 사용된다.
^ 켈러, F. J. 게티스, W. E. 외 연구진(1993) 페이지 28-29
^ Riley, K. F.; Hobson, M. P.; Bence, S. J. (2010). Mathematical methods for physics and engineering. Cambridge University Press. ISBN 978-0-521-86153-3.
^ Lipschutz, S.; Lipson, M. (2009). Linear Algebra. McGraw Hill. ISBN 978-0-07-154352-1.
^ Stewart, James (2001). "§2.8. The Derivative As A Function". Calculus (2nd ed.). Brooks/Cole. ISBN 0-534-37718-1.

참조

켈러, F. J. 게티스, W. E. 외 연구진(1993) "물리학: 고전적이고 현대적인" 2차 개정판 맥그로 힐 출판사.

외부 링크

Wikimedia Commons의 포지션(지오메트리)과 관련된 미디어

[1] 변위라는 용어는 주로 기계학에서 사용되는 반면, 번역은 기하학에서 사용된다.

[phys_keller-2] 켈러, F. J. 게티스, W. E. 외 연구진(1993) 페이지 28-29

[3] Riley, K. F.; Hobson, M. P.; Bence, S. J. (2010). Mathematical methods for physics and engineering. Cambridge University Press. ISBN 978-0-521-86153-3.

[4] Lipschutz, S.; Lipson, M. (2009). Linear Algebra. McGraw Hill. ISBN 978-0-07-154352-1.

[stewart-5] Stewart, James (2001). "§2.8. The Derivative As A Function". Calculus (2nd ed.). Brooks/Cole. ISBN 0-534-37718-1.

[1]

[2]

[3]

[4]

[5]

Search