시간확장

특수 상대성 이론
상대성 원리 상대성 이론 제형
기초 아인슈타인의 공준 관성 기준틀 광속 맥스웰 방정식 로렌츠 변환
결과들 시간확장 길이수축 상대론적 질량 질량-에너지 당량 동시성 상대성 이론 상대론적 도플러 효과 토머스 프리세션 상대론적 원반 벨의 우주선 역설 에렌페스트 역설
시공간 민코프스키 시공간 시공간 도표 월드라인 라이트콘
동역학 적정시간 고유 질량 4운동량
역사 전구체 갈릴레이 상대성 이론 갈릴레이 변환 에테르 이론
사람 아인슈타인 소머펠트 마이컬슨 몰리 피츠제럴드 헤르글로츠 로렌츠 푸앵카레 민코프스키 피조 아브라함 태어난 플랑크 폰 라우 에렌페스트 톨만 디랙
물리 포털 카테고리
v t

시간 팽창은 두 시계 사이의 상대 속도(특수 상대성) 또는 위치 사이의 중력 잠재력 차이(일반 상대성)로 인해 두 시계에 의해 측정된 경과 시간의 차이입니다. 지정되지 않은 경우 "시간 확장"은 일반적으로 속도로 인한 영향을 나타냅니다.

관찰자와 움직이는 시계 사이의 거리 변화로 인한 다양한 신호 지연(즉, 도플러 효과)을 보상한 후, 관찰자는 움직이는 시계가 관찰자 자신의 기준 프레임에 정지해 있는 시계보다 더 느리게 똑딱거리는 것으로 측정할 것입니다. 또한, 무거운 물체에 가까운 시계는 무거운 물체에서 더 멀리 떨어진 시계보다 더 적은 경과 시간을 기록할 것입니다.

상대성 이론에 대한 이러한 예측은 실험을 통해 반복적으로 확인되었으며, 예를 들어 GPS와 갈릴레오와 같은 위성 항법 시스템의 작동에서 실질적인 관심사입니다.^[1]

역사

로렌츠 인자에 의한 시간 팽창은 20세기로 접어들면서 여러 저자들에 의해 예측되었습니다.^[2][3] 조지프 라모르(1897)는 적어도 핵 주위를 도는 전자들의 경우, 개별 전자들은 자신들의 궤도에 해당하는 부분들을 $1\sqrt{\mathrm{}}$- v $\sqrt{2\frac{{}^{}}{}}$ $\sqrt{\frac{{c\mathrm{}}^{}}{}}$ ${\$의 비율로 더 짧게 기술한다고 썼습니다$.$^[4] 에밀 콘(1904)은 이 공식을 시계의 속도와 구체적으로 연관시켰습니다.^[5] 특수 상대성 이론의 맥락에서 알버트 아인슈타인(1905)은 이 효과가 시간 자체의 본질에 관한 것이라는 것을 보여주었고, 그는 또한 시간의 상호성이나 대칭성을 처음으로 지적했습니다.^[6] 그 후 헤르만 민코프스키(Hermann Minkowski, 1907)는 시간 확장의 의미를 더욱 명확히 한 고유 시간의 개념을 소개했습니다.^[7]

상대속도에 의한 시간확장

특수 상대성 이론은 관성 기준 프레임에 있는 관찰자의 경우 상대적으로 움직이는 시계가 기준 프레임에 정지한 시계보다 더 느리게 똑딱거리는 것으로 측정된다는 것을 나타냅니다. 이 경우를 특수 상대론적 시간 팽창이라고 부르기도 합니다. 상대 속도가 빠를수록 서로 간의 시간 팽창이 커지며, 빛의 속도(299,792,458 m/s)에 가까워질수록 시간이 느려져 정지합니다.

이론적으로, 시간 확장은 빠르게 움직이는 차량의 승객들이 짧은 시간 내에 미래로 더 나아가는 것을 가능하게 할 것입니다. 충분한 고속의 경우 효과가 극적입니다. 예를 들어, 1년의 여행은 지구에서의 10년에 해당할 수 있습니다. 실제로, 1g의 일정한 가속도는 인간이 한 번의 일생 동안 알려진 우주 전체를 여행할 수 있게 해줍니다.^[9]

그러나 현재의 기술이 우주 여행의 속도를 심각하게 제한하고 있기 때문에, 실제로 경험하는 차이는 아주 미미합니다: 약 7,700 m/s의 속도로 지구 궤도를 도는 국제 우주 정거장(ISS)에서 6개월 후에, 우주 비행사는 지구의 그것들보다 약 0.005초 더 적게 늙었을 것입니다.^[10] 우주 비행사 세르게이 크리칼레프와 세르게이 아브데예프는 둘 다 지구에서 지나간 시간에 비해 약 20 밀리초의 시간 팽창을 경험했습니다.^[11][12]

단순추론

시간 팽창은 특수 상대성 이론의 제2 공준에 의해 지시되는 모든 기준 프레임에서 관찰된 빛의 속도의 일정성으로부터 추론될 수 있습니다.^{[13][14][15][16]}

이러한 빛의 속도의 일정성은 직관과 달리 물질적 물체와 빛의 속도가 가산적이지 않다는 것을 의미합니다. 광원을 향해 이동하거나 광원에서 멀어짐으로써 빛의 속도를 더 크게 보이게 할 수 없습니다.

두 개의 거울 A와 B로 구성된 간단한 수직 시계를 생각해 보면, 그 사이에 빛의 펄스가 튀어나옵니다. 거울들의 분리는 L이고 시계는 빛 펄스가 거울 A에 닿을 때마다 한 번씩 째깍거립니다.

시계가 정지한 프레임(그림의 왼쪽 부분 참조)에서 광 펄스는 길이 2L의 경로를 추적하고 시계 주기는 2L를 광속으로 나눕니다.

시계의 정지 프레임(그림의 오른쪽 부분)에 대해 속도 v로 이동하는 이동하는 관찰자의 기준 프레임에서 광 펄스는 더 긴 각도의 경로를 추적하는 것으로 간주됩니다. 모든 관성 관측자의 빛의 속도를 일정하게 유지하려면 움직이는 관측자의 관점에서 이 시계의 주기를 길게 해야 합니다. 즉, 로컬 시계에 대해 움직이는 프레임에서 측정했을 때, 이 시계는 더 느리게 실행될 것입니다. 피타고라스 정리를 직접 적용하면 특수 상대성 이론을 잘 예측할 수 있습니다.

광 펄스가 경로를 추적하는 데 걸리는 총 시간은 다음과 같습니다.

하프 경로의 길이는 다음과 같이 알려진 양의 함수로 계산할 수 있습니다. 이 세 방정식에서 변수 D와 L을 제거하면 다음과 같은 결과가 나옵니다.

시계 자체의 프레임에서 시계$$δ t' ${\displaystyle \Delta$'}의 이동하는 관찰자의 주기가$$δ t${\displaystyle$ \Delta'}의 주기보다 길다는 사실을 표현합니다. 로렌츠 계수 감마(γ)는 다음과 같이 정의됩니다.

정지 프레임에서 공통 주기를 갖는 모든 시계는 이동 프레임에서 관찰할 때 공통 주기를 가져야 하기 때문에, 기계, 전자, 광학(예에서 동일한 수평 버전의 시계와 같은)의 다른 모든 시계는 동일한 속도 의존적 시간 팽창을 나타내야 합니다.^[18]

호혜성

특정 기준 프레임과 앞서 설명한 "정지된" 관찰자가 주어졌을 때, 만약 두 번째 관찰자가 "이동하는" 시계와 함께 동행한다면, 각 관찰자는 상대방의 시계가 자신의 로컬 시계보다 더 느린 속도로 똑딱거리는 것으로 인식할 것입니다. 둘 다 상대방을 자신의 정지된 기준틀에 상대적으로 움직이는 사람으로 인식하기 때문입니다.

움직이는 물체에 대해 시간의 흐름이 느려졌다면, 그 물체는 외부 세계의 시간을 관찰하여 그에 상응하는 속도를 낼 것이라는 것이 상식입니다. 반직관적으로 특수 상대성 이론은 그 반대를 예측합니다. 두 관측자가 서로에 대해 움직이고 있을 때, 각각은 관측자의 기준 프레임에 대해 움직이고 있는 것과 일치하여 서로의 시계가 느려지는 것을 측정합니다.

이것은 자기 모순처럼 보이지만 일상 생활에서도 유사한 이상 현상이 발생합니다. 두 사람 A와 B가 멀리서 서로를 관찰하면 B는 A에게 작게 보이지만 동시에 A는 B에게 작게 보일 것입니다. 원근법의 효과를 잘 알기 때문에 이 상황에는 모순이나 역설이 없습니다.^[19]

현상의 상호성은 또한 쌍둥이의 나이가 비교되는 이른바 쌍둥이 역설로 이어지는데, 하나는 지구에 머물고 다른 하나는 우주 여행에 나서는 것입니다. 그리고 상호성은 두 사람이 재회할 때 두 사람의 나이가 같아야 한다는 것을 암시합니다. 반대로 왕복이 끝나면 여행 쌍둥이는 지구에 있는 동생보다 더 어린 동생이 됩니다. 역설이 제기하는 딜레마는 상황이 대칭적이지 않다는 사실로 설명될 수 있습니다. 지구에 머무는 쌍둥이는 하나의 관성 프레임 안에 있고, 여행하는 쌍둥이는 두 개의 서로 다른 관성 프레임 안에 있습니다. 하나는 나가는 길이고 다른 하나는 돌아오는 길입니다. 또한 Twin paradox#가속도의 역할 참조.

실험시험

도플러 효과

• 아이브스와 스틸웰(1938, 1941)이 밝힌 이 실험의 목적은 운하 광선의 도플러 효과가 적절한 실험을 제공할 것이라는 아인슈타인의 제안을 사용하여 라모르-로렌츠 에테르 이론이 예측한 시간 팽창 효과를 검증하는 것이었습니다. 이 실험들은 바로 앞과 바로 뒤에서 보았을 때 음극선에서 방출되는 방사선의 도플러 이동을 측정했습니다. 감지된 고주파수와 저주파는 고전적으로 예측된 값이 아닙니다.
  $${\displaystyle {\frac {f_{0}}{1-v/c}}\qquad {\text{and}}\qquad {\frac {f_{0}}{1+v/c}}}$$

  
  이동 소스에서 나오는 방사선의 고주파수와 저주파는 다음과 같이 측정되었습니다.^[20]
  $${\displaystyle {\sqrt {\frac {1+v/c}{1-v/c}}}f_{0}=\gamma \left(1+v/c\right)f_{0}\qquad {\text{and}}\qquad {\sqrt {\frac {1-v/c}{1+v/c}}}f_{0}=\gamma \left(1-v/c\right)f_{0}\,}$$

  
  아인슈타인(1905)이 로렌츠 변환으로부터 추론한 바와 같이, 소스가 로렌츠 인자에 의해 느리게 실행될 때.
• Hasselkamp, Mondry 및 Scharmann^[21](1979)은 직각으로 움직이는 소스에서 시선으로 이동하는 도플러 이동을 측정했습니다. 이동 소스에서 나오는 방사선의 주파수 사이의 가장 일반적인 관계는 다음과 같습니다.
  $${\displaystyle f_{\mathrm {detected} =f_{\mathrm {rest} }{\left(1-{\frac {v}{c}}\cos \phi \right)/{\sqrt {1-{v^{2}}/{c^{2}}}}}$$

  
  아인슈타인(1905)^[22]이 추론한 바와 같이. ϕ = 90°(cos ϕ = 0)인 경우 f = f γ로 줄어듭니다. 이동원의 이 낮은 주파수는 시간 팽창 효과에 기인할 수 있으며 종종 횡방향 도플러 효과라고 불리며 상대성 이론에 의해 예측되었습니다.
• 2010년 시간 팽창은 광섬유 75미터로 연결된 광학 원자 시계를 사용하여 초당 10미터 미만의 속도로 관측되었습니다.^[23]

움직이는 입자

• 다른 속도에서 뮤온 수명을 비교할 수 있습니다. 실험실에서는 느린 뮤온이 생성되고 대기에서는 매우 빠르게 움직이는 뮤온이 우주선에 의해 유입됩니다. 정지 상태의 뮤온 수명을 2.197μs의 실험실 값으로 하면, 우주선이 생성한 뮤온의 수명이 빛의 98% 속도로 이동하는 것으로 관측된 것과 일치하여 약 5배 더 길어집니다. 로시와 홀(Rossi and Hall, 1941)은 산 정상에서 우주선이 생성된 뮤온의 개체수를 해수면에서 관측된 것과 비교했습니다.^[24]
• 입자 가속기에서 생성되는 입자의 수명은 시간 팽창으로 인해 더 깁니다. 이러한 실험에서 "시계"는 뮤온 붕괴로 이어지는 과정에 걸리는 시간이며, 이러한 과정은 움직이는 뮤온에서 자체적인 "시계 속도"로 이루어지며, 이는 실험실 시계보다 훨씬 느립니다. 이는 입자 물리학에서 일상적으로 고려되며 많은 전용 측정이 수행되었습니다. 예를 들어, CERN의 뮤온 저장 링에서 γ = 29.327로 순환하는 뮤온의 수명은 64.378μs로 확장된 것으로 밝혀졌으며, 0.9 ± 0.4ppm의 정확도로 시간 확장이 확인되었습니다.

적정 시간과 민코프스키 다이어그램

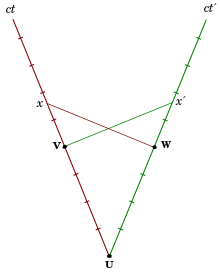
오른쪽 첫 번째 이미지의 민코프스키 다이어그램에서 관성 프레임 S'에서 쉬고 있는 시계 C는 d에서 시계 A와 f에서 시계 B를 만납니다(둘 다 S에서 쉬고 있습니다). 세 개의 시계가 동시에 S에서 똑딱거리기 시작합니다. A의 세계선은 ct축이고, f와 교차하는 B의 세계선은 ct축과 평행하며, C의 세계선은 ct'축입니다. S의 d와 동시에 발생하는 모든 이벤트는 x축에 있고, x'축의 S'에 있습니다.

두 이벤트 사이의 적절한 시간은 두 이벤트 모두에 존재하는 시계로 표시됩니다.^[26] 즉, 모든 관성 프레임에서 이 시간이 그 시계에 의해 표시된다는 것에 동의합니다. 따라서 df 간격은 시계 C의 적절한 시간이며, S에서 시계 B와 A의 좌표 시간 ef=dg에 비해 짧습니다. 반대로, B의 적절한 시간 ef도 S'에 있는 경우 시간과 관련하여 더 짧습니다. 왜냐하면 이벤트 e는 C가 틱을 시작하기 훨씬 전에 동시성 상대성 이론으로 인해 시간 i에서 이미 S'에서 측정되었기 때문입니다.

이를 통해 두 이벤트 모두에 존재하는 가속되지 않은 시계로 표시되는 두 이벤트 사이의 적절한 시간은 다른 모든 관성 프레임에서 측정된 동기화된 좌표 시간과 비교하여 항상 해당 이벤트 사이의 최소 시간 간격임을 알 수 있습니다. 그러나 두 이벤트 사이의 간격은 두 이벤트 모두에 존재하는 가속 클럭의 적절한 시간에 해당할 수도 있습니다. 두 사건 사이의 가능한 모든 적절한 시간에서 가속되지 않은 시계의 적절한 시간은 최대이며, 이것이 쌍둥이 역설의 해결책입니다.^[26]

도출 및 공식화

위에서 사용된 라이트 클럭 외에도 시간 확장에 대한 공식은 더 일반적으로 로렌츠 변환의 시간적 부분에서 파생될 수 있습니다.^[27] 이동 시계가 ${\$ 및$$ ${\displaystyle {tb}_{}}$ ${\$를 나타내는 두 가지 이벤트가 있다고 가정합니다$.$

${\displaystyle t_{a}^{\prime }={\frac {t_{a}-{\frac {vx_{a}}{c^{2}}}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},\ t_{b}^{\prime }={\frac {t_{b}-{\frac {vx_{b}}{c^{2}}}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

시계는 관성 프레임에서 $정지$ 상태를 유지하기 때문에 ${\displaystyle x_{}}$ a = ${\displaystyle x_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle x_{a$} = $x_{b}}$를 따르므로${\displaystyle {}^{}}$δ t' = ${\displaystyle t_{}^{}}$ ${\displaystyle {}_{}^{}}$ -$$t a' ${\displaystyle \Delta$ t^{\prime } = t_{$b}^{\prime }-$t_{$a}^{\$prime }}} 간격은 다음과 같습니다.

${\displaystyle \Delta t'=\gamma \,\Delta t={\frac {\Delta t}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\,}$

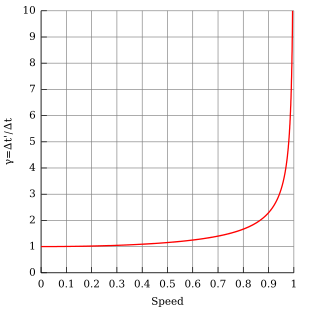
여기서 δt는 일부 관성 프레임(예: 시계의 눈금)에서 관찰자에 대한 두 개의 공동 로컬 이벤트(즉, 동일한 장소에서 발생) 사이의 시간 간격이며, 이를 적절한 시간, δ이라고 합니다.t′ 는 다른 관측자에 의해 측정된 동일한 사건들 사이의 시간 간격으로, 이전 관측자에 대해 관성적으로 속도 v로 이동하고, v는 관측자와 이동하는 시계 사이의 상대 속도, c는 광속, 로렌츠 계수(일반적으로 그리스 문자 감마 또는 γ로 표시됨)는 다음과 같습니다.

${\displaystyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}\,}$

따라서 움직이는 시계의 시계 주기 지속 시간은 증가하는 것으로 밝혀졌습니다. "느리게 작동"하는 것으로 측정됩니다. v ≪ c가 우주 여행을 고려하더라도 쉽게 감지할 수 있는 시간 확장 효과를 생성할 만큼 충분히 크지 않은 일반 생활에서 이러한 다양성의 범위는 대부분의 목적에서 안전하게 무시될 수 있습니다. 대략적인 임계값으로서, 물체가 30,000 km/s(광속의 1/10) 정도의 속도로 접근할 때 시간 확장이 중요해질 수 있습니다.^[28]

쌍곡 운동

특수 상대성 이론에서 시간 팽창은 상대 속도가 변하지 않는 상황에서 가장 간단하게 설명됩니다. 그럼에도 불구하고 로렌츠 방정식은 측정 기간 동안 g와 동일한 균일한(즉, 등속) 운동을 하는 일부 기준 물체에 대해 단위 질량당 힘으로 적용되는 우주선의 단순한 경우에 대한 적절한 시간과 공간 이동을 계산할 수 있도록 합니다.

나중에 나머지 프레임이라고 불리는 관성 프레임의 시간이라고 하자. x를 공간좌표라고 하고, 항가속도의 방향과 우주선의 속도(휴면틀 대비)를 x축에 평행하게 두도록 합니다. 시간 t = 0일 때 우주선의 위치를 x = 0으로 가정하고 속도를 v로 정의하고 다음과 같은 축약어를 정의합니다.

${\displaystyle \gamma _{0}={\frac {1}{\sqrt {1-v_{0}^{2}/c^{2}}}}}$

다음 공식은 다음과 같습니다.^[29]

위치:

${\displaystyle x(t)={\frac {c^{2}}{g}\left ({ {1+{\frac {\left(gt+v_{0}\gamma _{0}\right)^{2}}}-\gamma _{0}\right)}$

속도:

${\displaystyle v(t)={\frac {gt+v_{0}\gamma _{0}}{\sqrt {1+{\frac {\left(gt+v_{0}\gamma _{0}\right)^{2}}{c^{2}}}}}$

좌표 시간의 함수로서 적절한 시간:

${\displaystyle \tau(t)=\tau _{0}+\int _{0}^{t}{\sqrt {1-\left ({\frac {v(t')}{c}\right)^{2}}dt'}$

v(0) = v = 0이고 τ(0) = τ = 0인 경우 적분은 로그 함수 또는 이에 상응하는 역 쌍곡선 함수로 표현될 수 있습니다.

${\displaystyle \tau(t)={\frac {c}{g}\ln \left ({\frac {gt}{c}}+{\sqrt {1+\left ({\frac {gt}{c}}\right)^{2}}\right)={\frac {c}{g}}\operatorname{arsinh} \left ({\frac {gt}{c}\right)}$

선박의 적절한 시간$$τ${\displaystyle \$tau}의 함수로서 다음 공식이 성립합니다.

위치:

${\displaystyle x(\tau)={\frac {c^{2}}{g}\left(\cosh {\frac {g\tau }{c}-1\right)}$

속도:

${\displaystyle v(\tau)=c\tanh {\frac {g\tau }{c}}$

적절한 시간의 함수로서 시간 좌표:

${\displaystyle t(\tau)={\frac {c}{g}\sinh {\frac {g\tau }{c}}$

시계 가설

시계 가설은 시계가 시간 팽창에 의해 영향을 받는 속도가 가속도에 의존하지 않고 순간 속도에만 의존한다는 가정입니다. 이는 경로 $P{\displaystyle }$ ${\displaystyle$ P$}$을(를) 따라 이동하는 클럭이 다음으로 정의된 적절한 시간을 측정한다는$$ 것과 같습니다.

${\displaystyle \tau =\int _{P}{\sqrt {dt^{2}-dx^{2}/c^{2}-dy^{2}/c^{2}-dz^{2}/c^{2}}}}$

시계 가설은 아인슈타인의 1905년 특수 상대성 이론의 원래 공식에 암시적으로(명시적으로는 아니지만) 포함되었습니다. 그 이후로 표준 가정이 되었고 특히 입자 가속기의 매우 높은 가속까지의 실험적 검증에 비추어 볼 때 보통 특수 상대성 이론의 공리에 포함됩니다.^[31][32]

중력 또는 가속도에 의한 시간 팽창

중력 시간 팽창은 관측자가 중력 퍼텐셜 우물 내의 특정 고도에서 지역 시계가 더 높은 고도에 위치한 동일한 시계보다 더 적은 경과 시간을 측정한다는 것을 발견함으로써 경험됩니다.

예를 들어 ISS 우주 비행사의 경우 중력 시간 확장이 수행됩니다. 우주 비행사들의 상대 속도는 느려지지만, 그들의 위치에서 줄어든 중력의 영향력은 그 정도는 덜하지만 빨라집니다. 또한, 이론적으로 해발이 높은 사람들에 비해 산 정상에서 등반가의 시간은 약간 더 빠르게 흐르고 있습니다. 또한 시간 팽창으로 인해 지구의 핵은 지각보다 2.5년이나 어린 것으로 계산되었습니다.^[33] "지구가 완전히 자전하는 시간을 측정하는 데 사용되는 시계는 기준 지오이드 위의 고도 1km마다 하루에 약 10ns/day 더 긴 것으로 측정할 것입니다."^[34] 블랙홀 근처(사건의 지평선을 넘지는 않지만)와 같이 극도의 중력 시간 팽창이 일어나는 우주 지역으로 여행하면 빛에 가까운 속도의 우주 여행과 유사한 시간 이동 결과를 얻을 수 있습니다.

두 관측자 모두 다른 하나를 더 느리게 노화(역수 효과)로 측정하는 속도 시간 팽창과 달리 중력 시간 팽창은 역수가 아닙니다. 이것은 중력 시간 확장에 따라 두 관측자 모두 중력장 중심에 가까운 시계의 속도가 느리다는 것에 동의하고 그 차이의 비율에 동의한다는 것을 의미합니다.

실험시험

• 1959년 로버트 파운드와 글렌 A. 렙카는 지구의 중력장이 상대적으로 더 강렬한 낮은 높이에서 방출되는 빛의 진동수에서 매우 작은 중력 적색편이를 측정했습니다. 그 결과는 일반 상대성 이론 예측치의 10% 이내였습니다. 1964년 파운드와 J. L. 스나이더는 중력 시간 팽창으로 예측한 값의 1% 이내의 결과를 측정했습니다.^[35] (파운드-렙카 실험 참조)
• 2010년에는 광학 원자시계를 이용해 높이 차이가 1m에 불과한 지구 표면에서 중력 시간 팽창을 측정했습니다.^[23]

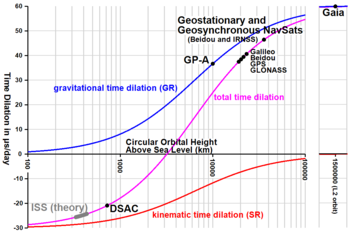
속도와 중력시간확장의 결합효과

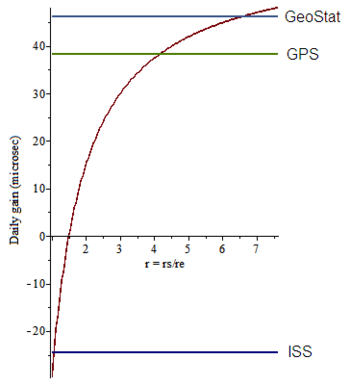
높은 정확도의 시간 유지, 저궤도 위성 추적 및 펄서 타이밍은 시간 확장을 생성할 때 질량과 운동의 결합 효과를 고려해야 하는 응용 프로그램입니다. 실용적인 예로는 국제 원자 시간 표준과 행성 간 물체에 사용되는 중심좌표 시간 표준과의 관계가 있습니다.

태양계와 지구에 대한 상대론적 시간 팽창 효과는 아인슈타인 필드 방정식에 대한 슈바르츠실트 해에 의해 매우 정확하게 모델링될 수 있습니다. 슈바르츠실트 메트릭에서 간격 ${\displaystyle {dT}_{}}$ E ${\$$E}}$은(는) 다음에 의해 제공됩니다.^[37][38]

${\displaystyle dt_{\text{E}}^{2}=\left(1-{\frac {2GM_{\text{i}}}{r_{\text{i}}c^{2}}}\right)dt_{\text{c}}^{2}-\left(1-{\frac {2GM_{\text{i}}}{r_{\text{i}}c^{2}}}\right)^{-1}{\frac {dx^{2}+dy^{2}+dz^{2}}{c^{2}}}}$

위치:

• ${\$$E}}$은(는) 적절한 시간 ${\displaystyle t_{}}$ ${\$의 작은 증분입니다.$E}}($원자시계에 기록할 수 있는 간격),
• ${\displaystyle {}_{}}$ ${\displaystyle c_{}}$ ${\$는 좌표 ${\displaystyle {tc}_{}}$ ${\$좌표 시간)에서 작은 증가입니다.
• ${\displaystyle d}$ ${\displaystyle x,}$ ${\displaystyle \mathrm{dy},}$ ${\displaystyle \mathrm{dz}}$ ${\displaystyle dx$}는 시계 위치의 세${\displaystyle \mathrm{좌표}}$x,$,z$ {\$displaystyle$x,y,z}에서 작은 증분입니다.
• ${\displaystyle \frac{-}{}}{\displaystyle \frac{}{{GMiri}_{}}}$ ${\$은 시계로부터$$ 거리 ${\displaystyle {ri}_{}}$ ${\$를 기준으로 이웃의 질량으로 인한 뉴턴 중력 전위의 합을 나타냅니다$$. 이 합계에는 모든 조석 잠재력이 포함됩니다.

일반 상대성 이론
${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={\kappa }T_{\mu \nu }}$
소개 역사 타임라인 테스트 수학 공식화
기본개념 등가원리 특수 상대성 이론 월드라인 의사 리만 다양체
현상 케플러 문제 중력렌즈 중력 적색편이 중력시간확장 중력파 프레임 드래그 측지효과 이벤트 지평선 특이점 블랙홀 시공간 시공간 도표 민코프스키 시공간 아인슈타인-로젠 다리
등식 형식주의 등식 선형화 중력 아인슈타인 장방정식 프리드만 측지학 Mathisson–Papapetrou–Dixon 해밀턴-자코비-아인슈타인 형식주의 ADM BSSN 포스트뉴턴어 고급이론 칼루자-클라인 이론 양자중력
솔루션 슈바르츠실트 (실내) 리스너-노르트스트롬 괴델 커 커-뉴먼 커-뉴먼-드 시터 카스너 레마 î 트레-톨만 타우브-넛 밀른 로버트슨-워커 오펜하이머-스나이더 pp파 밴스톡텀더스트 Weyl−Lewis−Papapetrou
사이언티스트 아인슈타인 로렌츠 힐베르트 푸앵카레 슈바르츠실트 드 시터 리스너 노르드스트롬 웨일 에딩턴 프리드먼 밀른 즈위키 레마 î 트레 오펜하이머 괴델 휠러 로버트슨 바딘 워커 커 찬드라세카르 엘러스 펜로즈 호킹 Raychaudhuri 테일러 헐스 반스톡툼 타우브 뉴먼 야우 쏜 다른이들
물리 포털 카테고리
v t

시계의 좌표 속도는 다음과 같습니다.

${\displaystyle v^{2}={\frac {dx^{2}+dy^{2}+dz^{2}}{dt_{\text{c}}^{2}}}}$

좌표 시간 ${\displaystyle {tc}_{}}$ ${\displaystyle t_{c}$는 모든 중력 질량에서 무한히 멀리 떨어져 있고(${\displaystyle \mathrm{U}}$ = 0 ${\displaystyle$ U$$=$0$$}),$ 좌표 시스템에서 정지해 있는 가상의 "좌표 시계"에서 읽을 수 있는 시간입니다($$ = ${\displaystyle 0}$ ${\displaystyle$ v= 0$}).$ 속도의 방사형 성분이 있는 시계의 적절한 시간의 비율과 좌표 시간의 비율 사이의 정확한 관계는 다음과 같습니다.

${\displaystyle {\frac {dt_{\text}E}}}{dt_{\text{c}}}}={\sqrt {1+{\frac {2U}{c^{2}}}-{\frac {v^{2}}{c^{2}}}+\left({\frac {c^{2}}{2U}}+1\right)^{-1}{\frac {{v_{\단평행}}^{2}}{c^{2}}}={\sqrt {1-\left(\beta ^{2}+\beta_{e}^{2}+{\frac {beta_{\단평행}^{2}\beta_{e}^{2}}{1-\beta_{e}^{2}}}\right)}}}$

위치:

• $v ∥$ {\$displaystyle v_${\단평행$}}$은 반경 방향 속도입니다.
• $=$$GM_{i}}{r_{i}}}$는 탈출 속도이며,
• ${\displaystyle \beta }$ =$$$v$ /${\displaystyle c}$ ${\displaysty$$$= $v$/$c$$\},$ ${\displaystyle \beta }$ e =$$v${\displaystyle {}_{}}$/ ${\displaystyle c}${\$displaysty$${\displaystyle \mathrm{le\; \backslash }}$$beta$$_$${\displaystyle \{}$e} =$$v_{e}/$c$ ${\displaystyle 및}$${\displaystyle \beta }$${\displaystyle }$∥$$${\displaystyle =}$ $v$ ∥ / c ${\displaysty$${\displaystyle \mathrm{le\; \backslash }}$beta _${\단$${\displaystyle 평}$$행}$ = v_{\단평행}/c}는 빛의 속도 c에 대한 백분율로서 속도입니다.
• ${\displaystyle U}$ $=$- ${\displaystyle \frac{G}{}}$ ${\displaystyle \frac{{Miri}_{}}{}}$ ${\displaysty$U={\$frac {-GM_{i}}{r_{i}}$는 뉴턴 퍼텐셜이므로${\displaystyle U}$ ${\displaystyle -U}$는 탈출 속도의 절반과 같습니다.

위의 방정식은 슈바르츠실트 해의 가정 하에서 정확합니다. 움직임이 있거나 중력이 없는 경우, 즉 $\beta$ ${\displaystyle \mathrm{e}}$ = 0 ${\displaystyle \$beta _{e} = 0으로 감소합니다. 움직임이 없고 중력이 없는 경우, 즉 $\beta$ = 0 = $β$∥ ${\displaystyle$ \beta =$$0 = beta _$\{\backslash$단평행}} 중력 시간 팽창 방정식으로 줄어듭니다.

실험시험

• 1971년, 하펠레와 키팅은 상업용 여객기를 타고 세슘 원자시계를 지구의 동서로 날리며, 경과 시간을 미국 해군 관측소에 남아 있는 시계와 비교했습니다. 두 가지 상반된 효과가 작용했습니다. 시계는 대부분의 여행에서 더 높은 (약한) 중력 잠재력에 있었기 때문에 기준 시계보다 더 빨리 노화될 것으로 예상되었습니다 (더 큰 경과 시간을 보여줍니다). 하지만 대조적으로, 움직이는 시계들은 이동 속도 때문에 더 천천히 노화될 것으로 예상되었습니다. 이론은 각 여행의 실제 비행 경로를 통해 미 해군 관측소의 기준 시계와 비교하여 비행 시계가 동쪽 여행에서 40±23나노초를 잃어야 하고 서쪽 여행에서 275±21나노초를 얻었어야 한다고 예측했습니다. 미국 해군 관측소의 원자 시간 척도에 비해 비행 시계는 동쪽으로 이동하는 동안 59±10 나노초를 잃었고 서쪽으로 이동하는 동안 273±7 나노초를 얻었습니다(오차 막대는 표준 편차를 나타냅니다).^[39] 2005년, 영국의 국립 물리 연구소는 이 실험을 제한적으로 복제했다고 보고했습니다.^[40] NPL 실험은 세슘 시계를 더 짧은 여행(런던-워싱턴 D.C. 리턴)으로 보냈다는 점에서 원래와 다르지만 시계는 더 정확했습니다. 보고된 결과는 상대성 예측치의 4% 이내이며, 측정치의 불확실성 내에 있습니다.
• 지구 위치 측정 시스템은 특수 상대성 이론과 일반 상대성 이론 모두에서 지속적으로 작동하는 실험으로 간주될 수 있습니다. 궤도 내 시계는 위에서 설명한 대로 특수 상대론적 시간 팽창 효과와 일반 상대론적 시간 팽창 효과 모두에 대해 보정되어 지구 표면의 시계와 동일한 속도로 작동합니다.^[41]

대중문화에서

속도와 중력 시간 팽창은 다양한 미디어에서 공상과학 작품의 주제였습니다. 영화 속의 몇몇 예들은 인터스텔라와 혹성탈출입니다.^[42] 인터스텔라에서 핵심 플롯 포인트는 회전하는 블랙홀에 가깝고 시간 팽창으로 인해 표면에서 1시간이 지구에서 7년에 해당하는 행성을 포함합니다.^[43] 물리학자 Kip Thorne은 그 영화를 만드는데 협력했고 인터스텔라의 과학이라는 책에서 그것의 과학적인 개념들을 설명했습니다.^[44][45]

시간 확장은 블랙홀 근처 우주선에서 벌어지는 닥터 후 에피소드 "World Enough and Time"과 "The Doctor Falls"에서 사용되었습니다. 블랙홀의 엄청난 중력과 배의 길이(400마일) 때문에 시간은 한쪽 끝에서 다른 쪽 끝보다 더 빠르게 움직입니다. 닥터의 동반자인 빌이 배의 다른 쪽 끝으로 끌려갈 때, 그녀는 몇 년 동안 그가 그녀를 구출해 주기를 기다립니다. 그의 시간에는 몇 분밖에 지나지 않습니다.^[46] 또한 확장 기능을 통해 사이버맨은 이전에 방송에서 볼 수 있었던 것보다 "더 빠른" 속도로 진화할 수 있습니다.

폴 앤더슨의 소설 타우 제로는 SF 문학에서 이 개념의 초기 예입니다. 소설에서, 우주선은 부사드 램제트를 사용하여 승무원들이 탑승하는데 5년이 걸릴 정도의 빠른 속도로 가속하지만, 그들이 목적지에 도착하기 전에 33년이 지구를 지나갑니다. 속도 시간 팽창은 배가 빛의 속도에 가까워질수록 점점 더 0에 가까워지는 타우 계수의 관점에서 설명되며, 따라서 소설의 제목입니다.^[47] 사고로 인해 승무원들은 우주선의 가속을 멈출 수 없어 우주의 끝에서 승무원들이 빅 크런치를 경험할 정도로 극심한 시간 팽창을 일으키고 있습니다.^[48] 로캐넌의 세계, 히페리온, 영원한 전쟁과 같은 문학의 다른 예들도 비슷하게 상대론적 시간 팽창을 과학적으로 그럴듯한 문학적 장치로 사용하여 특정 인물들이 우주의 나머지 부분보다 더 느리게 늙도록 합니다.^[49][50]

참고 항목

• 길이수축
• 특수 상대성 이론의 질량

각주

참고문헌

추가읽기

• Callender, C.; Edney, R. (2001). Introducing Time. Icon Books. ISBN 978-1-84046-592-1.
• Einstein, A. (1905). "Zur Elektrodynamik bewegter Körper". Annalen der Physik. 322 (10): 891. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004.
• Einstein, A. (1907). "Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips". Annalen der Physik. 328 (6): 197–198. Bibcode:1907AnP...328..197E. doi:10.1002/andp.19073280613.
• Hasselkamp, D.; Mondry, E.; Scharmann, A. (1979). "Direct Observation of the Transversal Doppler-Shift". Zeitschrift für Physik A. 289 (2): 151–155. Bibcode:1979ZPhyA.289..151H. doi:10.1007/BF01435932. S2CID 120963034.
• Ives, H. E.; Stilwell, G. R. (1938). "An experimental study of the rate of a moving clock". Journal of the Optical Society of America. 28 (7): 215–226. Bibcode:1938JOSA...28..215I. doi:10.1364/JOSA.28.000215.
• Ives, H. E.; Stilwell, G. R. (1941). "An experimental study of the rate of a moving clock. II". Journal of the Optical Society of America. 31 (5): 369–374. Bibcode:1941JOSA...31..369I. doi:10.1364/JOSA.31.000369.
• Joos, G. (1959). "Bewegte Bezugssysteme in der Akustik. Der Doppler-Effekt". Lehrbuch der Theoretischen Physik, Zweites Buch (11th ed.).
• Larmor, J. (1897). "On a dynamical theory of the electric and luminiferous medium". Philosophical Transactions of the Royal Society. 190: 205–300. Bibcode:1897RSPTA.190..205L. doi:10.1098/rsta.1897.0020. (같은 이름을 가진 일련의 논문에서 세 번째이자 마지막입니다.)
• Poincaré, H. (1900). "La théorie de Lorentz et le principe de Réaction". Archives Néerlandaises. 5: 253–78.
• Puri, A. (2015). "Einstein versus the simple pendulum formula: does gravity slow all clocks?". Physics Education. 50 (4): 431. Bibcode:2015PhyEd..50..431P. doi:10.1088/0031-9120/50/4/431. S2CID 118217730.
• Reinhardt, S.; et al. (2007). "Test of relativistic time dilation with fast optical atomic clocks at different velocities" (PDF). Nature Physics. 3 (12): 861–864. Bibcode:2007NatPh...3..861R. doi:10.1038/nphys778. Archived from the original (PDF) on 2009-07-12.
• Rossi, B.; Hall, D. B. (1941). "Variation of the Rate of Decay of Mesotrons with Momentum". Physical Review. 59 (3): 223. Bibcode:1941PhRv...59..223R. doi:10.1103/PhysRev.59.223.
• Weiss, M. "Two way time transfer for satellites". National Institute of Standards and Technology. Archived from the original on 2017-05-29.
• Voigt, W. (1887). "Über das Doppler'sche princip". Nachrichten von der Königlicher Gesellschaft der Wissenschaften zu Göttingen. 2: 41–51.

외부 링크

• Merrifield, Michael. "Lorentz Factor (and time dilation)". Sixty Symbols. Brady Haran for the University of Nottingham.