솔리드 지오메트리

수학에서, 입체 기하학 또는 입체 기하학은 3차원^[1] 유클리드 공간의 기하학(즉, 3D 기하학)에 대한 전통적인 이름이다.

입체측정학은 피라미드, 프리즘 및 기타 다면체, 원기둥, 원추체, 잘린 원추체, ^[2]구체로 둘러싸인 공 등 다양한 입체 도형(또는 3D 도형)의 체적 측정을 다룬다.

역사

피타고라스인들은 규칙적인 고체를 다루었지만 피라미드, 프리즘, 원추체, 원통체 등은 플라톤주의자들이 연구하기 전까지 연구되지 않았다.에우독소스는 피라미드와 원뿔이 같은 베이스와 같은 높이의 프리즘과 실린더의 1/3 부피를 가지고 있다는 것을 증명하면서 그들의 측정을 확립했다.그는 또한 구로 둘러싸인 부피가 ^[3]반지름의 세제곱에 비례한다는 증거를 발견한 사람일 것이다.

토픽

솔리드 지오메트리 및 입체 측정의 기본 토픽은 다음과 같습니다.

상세 토픽은 다음과 같습니다.

3차원의 투영 기하학(추가 차원을 사용함으로써 데사르게의 정리의 증명으로 이끈다.
추가 다면체
기술 기하학

실체 수치

구체는 공의 표면이지만, 용어가 도형의 표면 또는 그 안에 둘러싸인 부피, 특히 실린더를 가리키는 것이 애매한 경우가 있습니다.다음 표에는 볼륨을 구성하거나 정의하는 주요 유형의 도형이 포함되어 있습니다.

그림	정의들	이미지들
평행관	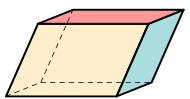각각 평행사변형인 6개의 면(육면체)을 가진 다면체 세 쌍의 평행면이 있는 육면체 밑면이 평행사변형인 프리즘
마름모꼴	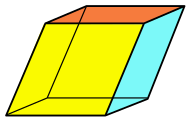모든 모서리의 길이가 동일한 평행입방체 정육면체. 단, 면은 정사각형이 아니라 마름모꼴이다.
입방체	6개의 사각형 면으로 둘러싸인 볼록한 다면체로, 그 다면체 그래프는 입방체와^[4] 같다. 일부 소스에서는 각 면이 직사각형이어야 하므로 인접한 면의 각 쌍이 직각으로 만난다.이 보다 제한적인 형태의 입방체는 직사각형 입방체, 오른쪽 입방체, 직사각형 상자, 직사각형 육면체, 오른쪽 직사각형 프리즘 또는 직사각형 ^[5]입방체로도 알려져 있습니다.
다면체	평면 다각형 면, 직선 모서리 및 날카로운 모서리 또는 정점	작은 젤리 모양의 12면체 트로이덜 다면체
균일한 다면체	정다각형은 면으로서 정점-추이적이다(즉, 정점을 다른 정점에 매핑하는 등각도가 있다).	사면체 스누브 12면체
프리즘	n면 다각형 베이스, 첫 번째 베이스의 번역된 복사(회전하지 않고 견고하게 이동)인 두 번째 베이스 및 두 개의 베이스의 대응하는 변을 접합하는 n개의 다른 면(필요한 모든 평행사변형)으로 이루어진 다면체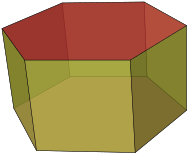
원뿔	평탄한 베이스(대부분 원형은 아니지만)에서 정점 또는 정점이라고 불리는 점까지 부드럽게 테이퍼링합니다.	우측 원형 원뿔과 경사 원형 원뿔
실린더	직선 평행한 면과 원형 또는 타원형	고체 타원 원통 우측 및 경사 원통
타원체	방향 비늘 또는 보다 일반적으로 아핀 변환에 의해 변형함으로써 구체에서 얻을 수 있는 표면	${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:$ x ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:$ ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:$ 2 + ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:$ ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:$ ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:$ 2 + ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:$ ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:$ ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:$ ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:$ ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:$ : ${\style$ { $x^2$ } \ $over$ a $^{2}$ + { $y^{2} \over$ b $^{2}$ + { $z^{2}$ \ $over$ c $^{2} = 1:}$ 인 타원체의 예 구체(상단, a=b=c=4) 구형(왼쪽 아래, a=b=5, c=3) 3중 타원체(오른쪽 아래, a=4.5, b=6, c=3)
레몬	렌즈(또는 ^[6]원호의 절반 미만)의 끝을 통과하는 축을 중심으로 회전하는 렌즈
쌍곡선	주축 중 하나를 중심으로 쌍곡선을 회전시켜 생성되는 표면

기술

솔리드 지오메트리에 다양한 기술과 도구가 사용됩니다.그 중에서도 해석기하학 및 벡터기법은 고차원에 중요한 선형방정식과 행렬대수를 체계적으로 사용할 수 있게 함으로써 큰 영향을 준다.

적용들

입체 기하학 및 입체 측정의 주요 응용 분야는 3D 컴퓨터 그래픽입니다.

「」를 참조해 주세요.

메모들

^ The Britannica Guide to Geometry, Britannica Educational Publishing, 2010, 페이지 67-68.
^ Kiselev 2008.
^ 1911년판 브리태니커 백과에서 일부 인용한 것이다.
^ Robertson, Stewart Alexander (1984). Polytopes and Symmetry. Cambridge University Press. p. 75. ISBN 9780521277396.
^ Dupuis, Nathan Fellowes (1893). Elements of Synthetic Solid Geometry. Macmillan. p. 53. Retrieved December 1, 2018.
^ Weisstein, Eric W. "Lemon". Wolfram MathWorld. Retrieved 2019-11-04.

레퍼런스

Kiselev, A. P. (2008). Geometry. Vol. Book II. Stereometry. Translated by Givental, Alexander. Sumizdat.

[1] The Britannica Guide to Geometry, Britannica Educational Publishing, 2010, 페이지 67-68.

[2] Kiselev 2008.

[3] 1911년판 브리태니커 백과에서 일부 인용한 것이다.

[4] Robertson, Stewart Alexander (1984). Polytopes and Symmetry. Cambridge University Press. p. 75. ISBN 9780521277396.

[5] Dupuis, Nathan Fellowes (1893). Elements of Synthetic Solid Geometry. Macmillan. p. 53. Retrieved December 1, 2018.

[mathworld-6] Weisstein, Eric W. "Lemon". Wolfram MathWorld. Retrieved 2019-11-04.

[1]

[2]

[3]

[4]

[5]

[6]

Search

솔리드 지오메트리

네임스페이스

더

목차

역사

토픽

실체 수치

기술

적용들

「」를 참조해 주세요.

메모들

레퍼런스

Search

솔리드 지오메트리

역사

토픽

실체 수치

기술

적용들

「 」를 참조해 주세요.

메모들

레퍼런스

「」를 참조해 주세요.