크레이머의 역설

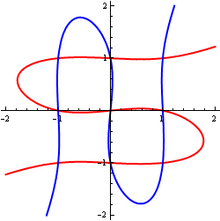
수학에서 Cramer의 역설(Cramer's paradox) 또는 Cramer-Euler paradox는^[1] 평면에서 두 개의 고차 곡선의 교점 수가 하나의 곡선을 정의하는 데 일반적으로 필요한 임의의 점의 수보다 많을 수 있다는 진술입니다. 이름은 제네반 수학자 가브리엘 크레이머의 이름을 따서 지어졌습니다.

이 현상은 교점이 수가 많음에도 불구하고 어떤 곡선(적어도 두 개의 다른 곡선에 속함)을 고유하게 정의하지 못하기 때문에 역설적으로 나타납니다. 이것은 순진한 이해의 결과이거나 두 가지 정리를 잘못 적용한 결과입니다.

• Bézout의 정리는 특정한 필요 조건이 충족된다면 두 대수 곡선의 교점 수는 그들의 차수의 곱과 같다는 것을 말합니다. 특히$,$ $n$도 {\$displaystyle$ n$}$인 두 곡선은$$ $일반적$으로 ${\displaystyle {n2\mathrm{}}^{}}${\$displaystyle$ n$^{2}}$개의$$ 교점을 갖습니다.
• Cramer의 정리에 $따르면{\displaystyle }$ n도 ${\displaystyle$ n$}$의 곡선은 $n{\displaystyle (\mathrm{n}}$+ 3${\displaystyle }$)${\displaystyle }$/ 2 ${\displaystyle$ n$(n$+ $3)/2}$ 포인트로$$ 결정되며$$, 다시 특정 조건이 성립한다고 가정합니다.

모든 $n개의$≥ 3 ${\displaystyle$n$\backslash$geq 3}에 대해 n 2개의 ≥ n(n + 3 ) / 2 {\displaystyle n^{2}\geq n(n + 3)/2}이므로 차수 3 이상의 경우 두 곡선의 교점은 두 곡선 중 하나를 고유하게 정의하기에 충분한 점을 갖는 것으로 나타납니다. 그러나 이 점들은 두 곡선 모두에 속하므로 이 정도의 고유한 곡선을 정의하지 않습니다. 역설의 해상도는 곡선을 정의하는 데 필요한 점 수에 $n{\displaystyle }$(${\displaystyle n}$+ ${\displaystyle 3}$)${\displaystyle }$/ 2 ${\displaystyle n(n$+ $3)/2}$이(가$$) 일반 위치의 점에만 적용된다는 것입니다. 축퇴된 특정 $경우$에는${\displaystyle }$n${\displaystyle (n}$ + ${\displaystyle 3}$) / ${\displaystyle 2\mathrm{}}${\$displaystyle$n($n$+ $3)/2}$개의$$ 점이 곡선을 고유하게 결정하기에 충분하지 않습니다.

역사

이 역설은 1720년 콜린 매클로린에 의해 처음 출판되었습니다.^[2][3] 크레이머와 레온하르트 오일러는 1744년과 1745년의 문자로 패러독스에 대해 서신을 주고받았고 오일러는 크레이머에게 문제를 설명했습니다.^[4] 비록 크레이머가 Maclaurin을 성명의 출처로 인용했지만, 그것은 그의 1750년 저서 "Introduction "al'analyle designes courbes algébriques"에 등장한 후 크레이머의 역설로 알려지게 되었습니다.^[5] 거의 비슷한 시기에 오일러는 9점으로^[4][6] 유일하게 정의되지 않은 3차 곡선을 보여주는 예들을 발표했고, 그의 저서 인니토럼에서 문제를 논의했습니다. 그 결과는 제임스 스털링에 의해 발표되었고 줄리어스 플뤼커에 의해 설명되었습니다.^[1]

선과 비퇴화 원뿔에 대한 역설 없음

1차 곡선(즉, 선)의 경우 $역설$이 발생하지 않습니다$.$ $n$ = 1 {\displaystyle n = 1}, son 2 = 1 < n (n + 3 ) / 2 = 2 {\displaystyle n^{2} = 1 < n (n + 3) / 2 = 2}이기 때문입니다. 일반적으로 두 개의 서로 다른 선은 동일한 기울기가 아닌 한 점에서 교차하며, 이 경우에는 전혀 교차하지 않습니다. 하나의 점으로는 선을 정의하기에 충분하지 않습니다(두 개가 필요합니다). 교차점을 통해 주어진 두 개의 선뿐만 아니라 무한히 많은 다른 선들도 통과합니다.

두 개의 퇴화되지 않은 원뿔들은 실제 평면에서 기껏해야 네 개의 유한한 점에서 교차하는데, 이것은 정확히 베조우트의 정리에 의해 최대로 주어진 숫자입니다. 그러나 비퇴행 원뿔을 정의하려면 5개의 점이 필요하므로 이 경우에도 역설은 없습니다.

입방 곡선에 대한 크레이머 예제

크레이머는 오일러에게 보낸 편지에서 입방 곡선 ${\displaystyle \mathrm{x}}$ ${\displaystyle 3{}^{}}$- x = 0 ${\displaystyle$x$^{3}-x$ = 0$}$ 및 y 3 - y = 0 {\displaystyle y^{3}-y = 0}이 정확히 9개의 점에서 교차한다고 지적했습니다. 첫 번째 방정식은 ${\displaystyle \mathrm{세}}$ 개의 수직선${\displaystyle }$x${\displaystyle }$= - 1 {\displaystyle $x$$$= - 1}, x = 0 {\displaystyle x = 0} 및 x = 1 {\displaystyle x = 1}을 정의하고, 마찬가지로 두 번째 방정식은 세 개의 수평선을 정의하며, 이 선들은 9개의 점으로 구성된 그리드에서 교차합니다. 따라서 9개의 점은 이와 같은 퇴화된 경우에서 입방 곡선을 고유하게 결정하기에 충분하지 않습니다.

결의안

n차의 이변량 방정식은 1 + n(n + 3) / 2 계수를 갖지만, 방정식을 계수 중 하나로 나누면 방정식에 의해 설명되는 점들의 집합은 보존되며, 한 계수는 1과 같고 n(n + 3) / 2 계수만 남겨져 곡선을 특성화합니다. n(n + 3) / 2개의 점_i(x_i, y)가 주어지면, 이 점들은 각각 n차의 일반 다항식에 대입하여 n(n + 3) / 2개의 방정식을 n(n + 3) / 2개의 미지수에서 선형으로 제공함으로써 별도의 방정식을 생성하는 데 사용될 수 있습니다. 이 시스템이 0이 아닌 행렬식을 갖는다는 의미에서 비퇴화적인 경우 미지의 계수가 고유하게 결정되고 따라서 다항식과 그 곡선이 고유하게 결정됩니다. 그러나 이 행렬식이 0이면 계는 퇴화되고 점들은 n도 곡선 이상에 있을 수 있습니다.

참고문헌

외부 링크

• 에드 샌디퍼 "크레이머의 역설"
• 수학 페이지의 크레이머의 역설