대수곡선

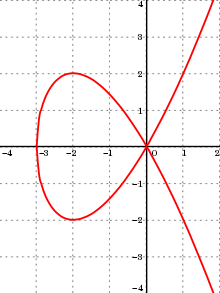
수학에서 아핀 대수 평면 곡선은 두 변수에 있는 다항식의 영점 집합이다. 투영 대수 평면 곡선은 세 변수에서 동종 다항식의 투영 평면에 설정된 0이다. 아핀 대수 평면 곡선은 정의 다항식을 균질화하여 투영 대수 평면 곡선에서 완성할 수 있다. 반대로 동질 방정식 h(x, y, t) = 0의 투영 대수 평면 곡선은 등식 h(x, y, 1) = 0의 아핀 대수 평면 곡선으로 제한할 수 있다. 이 두 연산은 각각 다른 연산과 반비례하므로 대수 평면 곡선이라는 구문은 고려되는 어핀인지 투영 사례인지를 명시적으로 명시하지 않고 자주 사용된다.

보다 일반적으로 대수적 곡선은 차원 1의 대수적 다양성이다. 동등하게 대수곡선은 대수 평면곡선과 비합리적으로 동등한 대수적 품종이다. 만약 곡선이 부속 공간이나 투영 공간에 포함되어 있다면, 그러한 쌍생 동등성에 대한 투영법을 취할 수 있다.

이러한 혼성 동등성은 대수 곡선 연구의 대부분을 대수 평면 곡선 연구로 감소시킨다. 그러나 일부 특성은 동등하게 유지되지 않으므로 비 평면 곡선에서 연구해야 한다. 특히 정도와 부드러움이 그렇다. 예를 들어, 0 속과 2도 이상의 부드러운 곡선이 존재하지만, 그러한 곡선의 평면 투영에는 단수 점이 있다(속-도 공식 참조).

비면 곡선은 흔히 공간 곡선 또는 스큐 곡선이라고 불린다.

유클리드 기하학에서

유클리드 평면의 대수곡선은 좌표가 이바리테이트 다항 방정식 p(x, y) = 0의 해법인 점들의 집합이다. 이 방정식은 종종 x의 함수로 명시적으로 y를 정의하는 함수의 그래프인 곡선과 대조적으로 곡선의 암묵적 방정식이라고 불린다.

그러한 암묵적 방정식에 의해 주어진 곡선으로, 첫 번째 문제는 곡선의 모양을 결정하고 그것을 그리는 것이다. 이러한 문제들은 함수 그래프의 경우처럼 해결하기가 쉽지 않은데, 이 경우 y는 x의 다양한 값에 대해 쉽게 계산될 수 있다. 정의 방정식이 다항식이라는 사실은 곡선이 이러한 문제를 해결하는 데 도움이 될 수 있는 구조적 특성을 가지고 있다는 것을 의미한다.

모든 대수적 곡선은 때로는 "제거할 수 있는 점"이라고 불리는 어떤 점들에 의해 연결되기도 하고, 어쩌면 acnode라고 불리는 한정된 수의 고립된 점들에 의해 때로는 매끄러운 모노톤 호(또는 가지라고도 함)의 유한한 수로 분해될 수 있다. 매끄러운 단조 원호는 x축의 개방된 간격에 단조 원과 정의되는 매끄러운 함수의 그래프다. 각 방향에서 호는 언바운드(일반적으로 무한 호라고 함)되거나 단일 점(이것은 아래에서 정의됨) 또는 좌표 축 중 하나에 평행한 접선이 있는 점인 끝점을 가진다.

예를 들어 Chchirnhausen 큐빅의 경우 끝점 기준으로 원점(0,0)을 갖는 두 개의 무한 호가 있다. 이 점이 곡선의 유일한 단수점이다. 또한 이 단수점을 하나의 끝점으로 가지고 있고 수평 접선을 가진 두 번째 끝점을 가지고 있는 두 개의 호가 있다. 마지막으로, 첫 번째 끝점으로 수평 접선이 있는 이러한 점 중 하나를 가지고 있고 두 번째 끝점으로 수직 접선이 있는 고유한 점을 가진 다른 두 개의 호가 있다. 이와는 대조적으로, 사인곡선은 확실히 대수 곡선이 아니며, 무한한 수의 단조 호를 가지고 있다.

대수적 곡선을 그리기 위해서는 주목할 만한 점과 그 접선, 무한한 가지와 그 무증상(있는 경우) 그리고 호가 그것들을 연결하는 방법을 아는 것이 중요하다. 변곡점을 주목할 만한 점으로 보는 것도 유용하다. 이 모든 정보가 종이에 그려질 때, 곡선의 모양은 대개 다소 선명하게 나타난다. 그렇지 않다면, 곡선에 대한 좋은 설명을 얻기 위해 몇 개의 다른 점들과 그 접선들을 추가하는 것으로 충분하다.

주목할 만한 점 및 그 접선의 계산 방법은 아래 평면 곡선의 주목할 만한 점 절에 설명되어 있다.

평면 투영 곡선

투영 공간에서는 곡선을 고려하는 것이 바람직할 때가 많다. 투사 평면 또는 평면 투사 곡선의 대수 곡선은 투사 좌표가 세 변수 P(x, y, z)에서 동종 다항식의 0인 투사 평면의 점들의 집합이다.

등식 p(x, y) = 0의 모든 아핀 대수곡선은 다음과 같은 경우$$ ${\displaystyle {}^{}}$ h p${\displaystyle (x,}$ y${\displaystyle ,\mathrm{z}}$ ) = 0${\displaystyle ,}$ ${\displaystyle ^{h}p(x,y,z)=0,}$의 투영곡선으로 완성될 수 있다.

p의 균질화의 결과인 것이다. 반대로 P(x, y, z) = 0이 투사곡선의 동종 방정식이라면, P(x, y, 1) = 0은 아핀 곡선의 방정식으로, 세 번째 투사 좌표가 0이 아닌 투사곡선의 점들로 구성된다. These two operations are reciprocal one to the other, as ${\displaystyle ^{h}p(x,y,1)=p(x,y)}$ and, if p is defined by ${\displaystyle p(x,y)=P(x,y,1)}$, then ${\displaystyle ^{h}p(x,y,z)=P(x,y,z),}$ as soon as the homogeneous 다항식 P는 z에 의해 분할되지 않는다.

예를 들어, 방정식²² x + y - z의² 투영곡선은 방정식 x² + y - 1² = 0의 단위 원의 투영완료다.

이는 아핀 곡선과 그 투영 완성이 동일한 곡선이라는 것을 의미하며, 더 정확히 말하면 아핀 곡선이 "완전" 곡선을 잘 정의할 수 있을 만큼 큰 투영 곡선의 일부라는 것을 의미한다. 이 관점은 일반적으로 아핀 곡선의 "무한도에서의 점"을 아핀 부분에 속하지 않는 투영완성의 점(한정수)으로 호출함으로써 표현된다.

투영 곡선은 종종 그들 자신을 위해 연구된다. 그것들은 또한 아핀 곡선의 연구에 유용하다. 예를 들어, p(x, y)가 아핀 곡선을 정의하는 다항식이라면, $부분파생상품{\displaystyle {}_{}^{}}$ p ${\displaystyle x_{}^{}}$′ ${\$${x}$ 및 $p{\displaystyle {}_{}^{}}$ ${\displaystyle y_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$ 옆에 있는 무한대에서 파생상품을 고려하는 것이 유용하다$.$

예를 들어, 한 점(a, b)에서 p(x, y) = 0의 아핀 곡선의 탄젠트 방정식은 다음과 같다.

평면 곡선의 주목할 만한 점

${\displaystyle {}^{}}$ 절에서는 p의 균질화 ${\displaystyle {}^{}(x}$, ${\displaystyle y}$ ,${\displaystyle z}$) = h p(x ,${\displaystyle y}$, z${\displaystyle }$) ${\displaystyle P(x,y,z)={}^{h}p(x,y,z)}}$에 의해 정의되는 이바리테이트 다항식 p(x, y)와 그 투영완료에 의해 정의된 평면 대수 곡선을 고려한다.

선과 교차점

주어진 선과 곡선의 교차점을 아는 것은 종종 유용하다. 좌표 축과 점근의 교차점은 곡선을 그리는 데 유용하다. 축에 평행한 선과 교차하면 곡선의 각 가지에서 최소한 한 점을 찾을 수 있다. 효율적인 루트 탐색 알고리즘이 가능한 경우, 이를 통해 y축에 평행한 모든 선으로 교차점을 표시하고 x축의 각 픽셀을 통과시켜 곡선을 그릴 수 있다.

곡선을 정의하는 다항식이 도 d를 갖는 경우, 어떤 선이든 대부분의 d 지점에서 곡선을 절단한다. 베주트의 정리는 이 숫자가 정확하게 d라고 주장하는데, 만약 그 점들이 대수적으로 닫힌 필드(예를 들어 복합적인 숫자)를 통해 투영면에서 검색되고, 그 다중성과 함께 세어진다. 뒤따르는 연산 방법은 이 정리를, 이 간단한 경우에 다시 증명한다.

등식 축+by+c = 0의 선으로 다항식 p에 의해 정의된 곡선의 교차점을 계산하려면 x(또는 a = 0인 경우 y)에 대한 선 방정식을 계산한다. 결과를 p로 대체하면, 선 방정식이 y로 해결된 경우 일변량 방정식 q(y) = 0(또는 q(x) = 0)을 얻게 되며, 각각의 뿌리는 교차로 점의 좌표 1개를 이룬다. 다른 좌표는 선의 방정식에서 추론한다. 교차점의 다중성은 해당 루트의 다중성이다. q의 정도가 p의 정도보다 낮으면 무한에 교차점이 있다; 무한에서 그러한 교차점의 다중성은 p와 q의 차이다.

점에서의 접선

The tangent at a point (a, b) of the curve is the line of equation ${\displaystyle (x-a)p'_{x}(a,b)+(y-b)p'_{y}(a,b)=0}$, like for every differentiable curve defined by an implicit equation. 다항식의 경우 탄젠트에 대한 다른 공식은 더 단순한 상수 항을 가지며 더 대칭적이다.

여기서 $p{\displaystyle {}_{\mathrm{}}^{}\infty (x}$, ${\displaystyle y}$)${\displaystyle }$= P ${\displaystyle z_{}^{}}$ ${\displaystyle {}_{}^{}}$(${\displaystyle x}$, ${\displaystyle \mathrm{y}}$, 1${\displaystyle }$) ${\displaystyle p'_{\inflt }(x,y)=$$P'_{z}(x,y,1)$은 무한에서$$ 파생된 것이다. 두 방정식의 등가성은 P에 적용된 오일러의 동질 함수 정리에서 비롯된다.

$p{\displaystyle {}_{}^{}}$ ${\displaystyle x_{}^{}}$ ${\displaystyle {}_{}^{}}$( ${\displaystyle a}$, b${\displaystyle }$)${\displaystyle }$= p ${\displaystyle y_{}^{}}$ ${\displaystyle {}_{}^{}}$( ${\displaystyle a}$, b${\displaystyle }$)${\displaystyle }$= ${\displaystyle 0,}$ ${\displaystyle p'_{x}(a,b)=p'_{y}(a,b)=0)$이면 접선이$$ 정의되지 않고 점이 단수점이다.

이는 즉시 투영 사례로 확장된다. 등식 P(x, y, z) = 0의 투사곡선의 투사좌표점(a:b:c)에서의 탄젠트 방정식은 다음과 같다.

그리고 단수인 곡선의 점들은 다음과 같은 점들이다.

(조건 P(a, b, c) = 0은 이러한 조건들에 의해, 오일러의 동질적 함수 정리에 의해 암시된다.)

점근목록

대수곡선의 모든 무한가지(infinite branch)는 곡선상 무한대의 한 점에 해당하며, 그것은 부속부에 속하지 않는 곡선의 투영완성의 한 점에 해당한다. 해당 점근은 그 점에서 곡선의 접선이다. 투영곡선에 접하는 일반적인 공식은 적용될 수 있지만, 이 경우에는 명시적으로 할 가치가 있다.

$p{\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle d_{}}$+ ${\displaystyle \cdots }$+ ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$ 곡선을 동질적인 부분으로 정의하는 다항식의 분해, 여기서$$ p는_i p 도 i의 단항 합이다. 그 뒤를 잇는다.

, 그리고

곡선의 무한대에 있는 점은 형태(a, b, 0)의 0이다. 동등하게, (a, b)는_d p의 0이다. 대수학의 근본적인 정리는 대수학적으로 폐쇄된 분야(일반적으로 복잡한 숫자의 분야)에_d 걸쳐 p 인자를 선형 인자의 산물로 만든다는 것을 암시한다. 각 인자는 곡선의 무한대에 점을 정의한다: bx - ay가 그러한 인자인 경우, 무한대에 점을 정의한다(a, b, 0). 실제에 걸쳐, p_d 요인은 선형 및 2차 인자로 된다. 불가역 2차 인자는 무한대에서 비실제 점을 정의하며, 실제 점들은 선형 인자에 의해 주어진다. 만일 (a, b, 0)이 곡선의 무한대에 있는 점이라면, 사람은 (a, b)가 점증하지 않는 방향이라고 말한다. 설정 q = p 해당_d 점근법의 방정식은

If ${\displaystyle q'_{x}(a,b)=q'_{y}(a,b)=0}$ and ${\displaystyle p_{d-1}(a,b)\neq 0,}$ the asymptote is the line at infinity, and, in the real case, the curve has a branch that looks like a parabola. 이 경우 곡선에 포물선이 있다고 한다. 만약

곡선은 무한대에 단수점을 가지며 몇 개의 점증상자를 가질 수 있다. 그것들은 단일 점의 접선 원뿔을 계산하는 방법에 의해 계산될 수 있다.

단수점

도 d의 다항식 p(x,y)에 의해 정의된 도 d 곡선의 단수점은 방정식 시스템의 해법이다.

특성 0에서 이 시스템은 여기서, 앞의 절의 표기법으로 $p{\displaystyle {}_{}^{}}$ ${\displaystyle {\infty \mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$( ${\displaystyle x}$, ${\displaystyle y}$)${\displaystyle }$= ${\displaystyle P_{}^{}}$ z ${\displaystyle {}_{}^{}}$( ${\displaystyle x}$, ${\displaystyle y}$, ${\displaystyle 1}$)${\displaystyle }$. ${\displaystyle p'_{\infit }(x,y)=$$P'_{z}(x,y,1)}$$$ 이 시스템은 오일러의 균일한 함수 정리 때문에 동등하다. 후자 시스템은 d 대신 d-1의 세 번째 다항식을 갖는 장점이 있다.

마찬가지로, 도 d의 균일한 다항식 P(x,y,z)에 의해 정의된 투영곡선의 경우, 단수점은 시스템의 해답을 가지고 있다.

균일한 좌표로 (양수 특성에서 방정식 $P{\displaystyle (x}$, y${\displaystyle }$, ${\displaystyle z}$) ${\displaystyle P(x,y,z)}$을(를) 시스템에 추가해야 한다$$.)

이것은 p(x,y) 또는 P(x,y,z)가 제곱이 없는 한 단수 점의 수가 유한하다는 것을 의미한다. 베주트의 정리는 따라서 단수점 수가 기껏해야 (d-1)이지만 방정식의 체계가 지나치게 정해져 있기 때문에 이 바운드는 날카롭지 않다.² 환원 가능한 다항식이 허용되는 경우, 첨예한 바운드는 d(d-1)/2이고, 이 값은 선형 요인의 다항 인자(곡선이 d선의 결합인 경우)에 도달한다. 불가해한 곡선 및 다항식의 경우, 단수점 수는 단수점(d-1)(d-2)/2로, 단수점(아래 참조)의 항으로 그 속을 표현하는 공식으로 인해 단수점 수는 기껏해야 (d-1)(d-2)(d-2)/2이다. 최대치는 모든 특이점들이 다중성 2와 구별되는 접선을 갖는 0 속 곡선에 의해 도달된다(아래 참조).

단수점에서 접선의 방정식은 단수점에서 다항식의 테일러 시리즈에서 가장 낮은 도에서 0이 아닌 균질 부분에 의해 주어진다. 단수점을 원점에 놓기 위해 좌표를 변경하면 단수점에 있는 접선의 방정식은 따라서 다항식의 가장 낮은 도에서 0이 아닌 균일한 부분이 되며, 단수점의 다중성은 이 균일한 부분의 정도가 된다.

분석구조

단수점 부근의 대수곡선의 분석구조 연구는 특이점의 위상에 대한 정확한 정보를 제공한다. 사실 단수점에 가까운, 실제 대수곡선은 단수점에서만 교차하고, 정점 또는 평탄한 곡선으로 보이는 한정된 수의 가지의 결합이다.

정규점 근처에서 곡선의 좌표 중 하나는 다른 좌표의 분석 함수로 표현될 수 있다. 이것은 분석적 암묵적 함수 정리의 코롤러리로, 곡선이 점 부근에 매끄럽다는 것을 내포하고 있다. 단수점에 가까운 상황은 더욱 복잡하고 가지들의 분석 파라메트릭 방정식을 제공하는 푸이섹스 시리즈를 포함한다.

특이점을 설명하기 위해서는 원점에 특이점이 있기 때문에 곡선을 번역할 가치가 있다. $이$는 X${\displaystyle }$= ${\displaystyle x}$- ${\displaystyle a,}$ Y${\displaystyle }$= ${\displaystyle y}$- ${\displaystyle b,}$ ${\displaystyle$ X$=x-a, Y=y-b}$ 형식의 변수 변경으로 구성되며${\displaystyle ,}$ ${\displaystyle \mathrm{여기}}$서 a , b ${\displaystyle a,b}$은(는) 단수 점의 좌표다. 다음에서 고려 중인 단수점은 항상 원점에 있게 되어 있다.

대수곡선의 방정식은 $f{\displaystyle (}$ ${\displaystyle x}$, ${\displaystyle y}$)${\displaystyle }$= ${\displaystyle 0,}$ ${\displaystyle f(x,y)=0,}$이며 여기서$$ f는 x와 y의 다항식이다. 이 다항식은 puiseux 시리즈의 대수적으로 닫힌 필드에 계수가 x인 y의 다항식으로 간주될 수 있다. 따라서 p는 ${\displaystyle \mathrm{puiseux}\mathrm{시리즈}}$인${\displaystyle }$y ${\displaystyle -}$P ( x ) , {\displaystyle $y-P(x)}$ 형식의 인자에 f를 포함시킬 수 있다$$. f가 수정 불가능한 다항식일 경우 이러한 요인은 모두 다르다. 이는 f가 계수의 영역과 독립적인 속성인 사각형이 없음을 의미하기 때문이다.

여기서 발생하는 Puiseux 시리즈는 그 형태를 가지고 있다.

여기서 d는 양의 정수이며, n ${\displaystyle {0\mathrm{}}_{}}$ ${\$은 원점을 통과하는 곡선의 가지만 고려하기 때문에 양수라고도 할 수 있는 정수다$$. 일반성을 상실하지 않는 한, ${\displaystyle \mathrm{우리}}$는 d가 ${\displaystyle n_{}}$ $≠$ 0 {\$displaystyle$a_${n$}\$neq 0}$과 같은 n의 가장 큰 공통점을 갖는 동시분모라고 가정할 수 있다($$그렇지 않으면, 지수에 대해 더 작은 공통분모를 선택할 수 있다).

$\Omega {\displaystyle {}_{}}$ ${\displaystyle d_{}}$ ${\$을(를) 단결의 원시 d번째 근원이 되게 하라$$. $위$의 Puiseux 시리즈가 f${\displaystyle }$( ${\displaystyle x}$, y${\displaystyle }$)${\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle f(x,y)=0}$의 인수화에서 발생하는 경우$,$ d 시리즈

인자화(갈루아 이론의 결과)에서도 발생한다. 이 d 시리즈는 합성이라고 하며, 라미화 지수 d의 곡선의 단일 분기로 간주된다.

실제 곡선의 경우, 즉 실제 계수를 갖는 다항식으로 정의된 곡선의 경우, 세 가지 사례가 발생할 수 있다. 실제 계수를 가진$$ P ${\displaystyle i_{}}$( ${\displaystyle x}$) ${\displaystyle P_{i}(x)$가 없으면 비현실 분기가 있는 것이다. 만약 어떤 P나는{\displaystyle P_{나는}())())}진짜 계수가 있다면, 한 P0()){\displaystyle P_{0}())로}. 만약 d이상한 경우 x의 모든 진정한 가치}P0()){\displaystyle P_{0}())의 진정한 값을 제공하고, 만약 d입니다. 비록, 1 색다르다, 규칙적인 보이는 실제 매장은 그것을 선택할 수 있다.만약 d 짝수인 ${\displaystyle \mathrm{경우}}$ ${\displaystyle {P\mathrm{}}_{}}$ 0${\displaystyle (}$ x$$) {\$displaystyle P_{0$}($x$$)}$ ${\displaystyle {및}_{}}$P ${\displaystyle {d\mathrm{}}_{}}$/ ${\displaystyle 2(}$x ) ${\displaystyle P_{d/2$}(x$)}$은(는) 실제$$ 값을 가지지만 x 0 0에만 해당된다. 이 경우 실제 가지(또는 사용되는 중단의 정의에 따라)는 중단으로 보인다.

예를 들어, 일반적인 첨탑은 하나의 가지만 가지고 있다. If it is defined by the equation ${\displaystyle y^{2}-x^{3}=0,}$ then the factorization is ${\displaystyle (y-x^{3/2})(y+x^{3/2});}$ the ramification index is 2, and the two factors are real and define each a half branch. If the cusp is rotated, it equation becomes ${\displaystyle y^{3}-x^{2}=0,}$ and the factorization is ${\displaystyle (y-x^{2/3})(y-j^{2}x^{2/3})(y-(j^{2})^{2}x^{2/3}),}$ with ${\displayst$$yle j=(1+{\sqrt{-3})/2}($계수$({\displaystyle {j\mathrm{}}^{}}$ 2${\displaystyle {}^{}{}^{}}$) ${\displaystyle {2\mathrm{}}^{}}$ ${\$${\displaystyle j}$$^{2})^{2}}$은 위의 ${\displaystyle {Pi}_{}}$( x${\displaystyle }$) ${\displaystyle P_{i}(x)})$의 정의가 어떻게 전문화되어 있는지를$$ 보여주기 위해 j로 단순화되지 않았다$$. 여기서 래미화 지수는 3이며, 오직 한 요소만이 실제적이다. 이는 첫 번째 경우에 두 요소가 동일한 분기를 정의하는 것으로 간주되어야 함을 보여준다.

비면 대수 곡선

대수적 곡선은 차원 1의 대수적 다양성이다. 이것은 치수 n의 부속 공간의 아핀 곡선이 n 변수의 n-1 다항식으로 정의된다는 것을 의미한다. 곡선을 정의하려면 이러한 다항식들이 Krull 치수 1의 원시 이상을 생성해야 한다. 이 상태는 실제 테스트가 쉽지 않다. 따라서 비면 곡선을 나타내는 다음과 같은 방법이 선호될 수 있다.

${\displaystyle {}_{}}$, ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$, ${\displaystyle {}_{}}$ ${\displaystyle {3\mathrm{}}_{}}$,${\displaystyle }$…${\displaystyle }$, ${\displaystyle g_{}}$ ${\$을(를) 두 변수 x와₁ x에서₂ f를 다시 해석할 수 없도록 한다. 좌표가 방정식과 불평등을 만족시키는 차원 n 부속 공간의 점

유한한 수의 점이 제거된 대수곡선의 모든 점들이다. This curve is defined by a system of generators of the ideal of the polynomials h such that it exists an integer k such ${\displaystyle g_{0}^{k}h}$ belongs to the ideal generated by ${\displaystyle f,x_{3}g_{0}-g_{3},\ldots ,x_{n}g_{0}-g_{n}}$. 이 표현은 f에 의해 정의된 곡선 및 평면 곡선 사이의 버라이어티 동등성이다. 모든 대수적 곡선은 이런 식으로 표현될 수 있다. 그러나 거의 항상 두 개의 첫 번째 변수에 투영을 주입하기 위해서는 변수의 선형 변경이 필요할 수 있다. 변수의 변경이 필요할 때, 거의 모든 변화는 무한의 영역에 걸쳐 정의되는 즉시 편리하다.

이 표현은 평면 투영의 해당 속성에서 그래픽 표현을 포함하여 비 평면 대수 곡선의 어떤 속성도 쉽게 추론할 수 있게 해준다.

그것의 암묵적 방정식에 의해 정의된 곡선의 경우, 위의 곡선의 표현은 더 작은 변수의 블럭이 (x₁, x₂)인 블록 순서에 대한 그뢰브너 기준에서 쉽게 추론할 수 있다. 다항식 f는 base에서₁₂ x와 x에만 의존하는 고유한 다항식이다. 분수 g_i/g는₀ x로_i 선형이고 x₁, x₂, x, x에만_i 의존하는 다항식을 선택함으로써 얻는다. 이러한 선택이 불가능할 경우 방정식은 다양성이 아닌 대수 집합을 정의하거나, 다양성이 차원 1이 아니거나, 좌표를 변경해야 함을 의미한다. 후자의 경우는 f가 존재하고 고유할 때 발생하며, i = 3, … n의 경우 선행 단수화가 x₁, x, x에만_2i 의존하는 다항식이 존재한다.

대수함수장

대수곡선의 연구는 두 개의 더 작은 곡선의 조합으로 쓸 수 없는 곡선의 반복적인 대수곡선의 연구로 축소될 수 있다. 쌍생 동등성까지, 필드 F에 대한 불가역 곡선은 F에 대한 하나의 변수에 있는 대수 함수 필드와 분류적으로 동등하다. 그러한 대수함수장은 F보다 초월적인 원소 x를 포함하는 F의 필드 확장자 K이며, 그러한 K는 F(x)의 유한 대수확장자로 F보다 불규칙한 x에서 이성함수의 영역이다.

예를 들어, C에서 합리적인 함수의 C(x) 필드를 정의할 수 있는 복잡한 숫자의 C 필드를 고려하십시오. y² = x³ - x - 1이면 C(x, y) 필드는 타원 함수 필드임. 원소 x는 고유하게 결정되지 않으며, 필드도 예를 들어 C(y)의 확장으로 간주할 수 있다. 함수장에 해당하는 대수곡선은 단순히² y = x - x³ - 1을 만족하는 C의² 점(x, y) 집합이다.

만약 필드 F가 대수적으로 닫히지 않는다면, 함수 필드의 관점은 예를 들어, 포인트가 없는 "곡선"을 포함하기 때문에 점의 위치를 고려하는 관점보다 약간 더 일반적이다. 예를 들어, 베이스 필드 F가 실수의 필드 R인 경우, x² + y = -1은² R(x)의 대수적 확장 필드를 정의하지만, R의² 서브셋으로 간주되는 해당 곡선은 포인트가 없다. x² + y² = -1 방정식은 체계적 의미(R보다 유한형의 적분된 1차원 체계)에서 R에 대한 불가역 대수적 곡선을 정의한다. 이러한 의미에서 F에 대한 불가역적 대수 곡선(생리 동등성까지)과 F에 대한 하나의 변수에 있는 대수 함수 필드 사이의 일대일 대응은 일반적으로 유지된다.

두 곡선은 곡선처럼 이형화되지 않고 비균등적으로 동등할 수 있다(즉, 이형화 함수 필드를 가질 수 있다). 비유동 곡선, 즉 특이점이 없는 곡선을 다룰 때 상황은 더 쉬워진다. 한 필드의 비정규 투사 곡선 2개는 함수 필드가 이형인 경우에만 이형이다.

Tsen의 정리는 대수적으로 닫힌 장에 대한 대수적 곡선의 함수 장에 관한 것이다.

복잡한 곡선 및 실제 표면

복잡한 투사 대수 곡선은 n차원 복합 투사 공간 CP에ⁿ 존재한다. 이것은 실제 다지관으로서 복잡한 치수 n을 가지지만 위상학적 치수는 2n이며, 콤팩트하고, 연결되고, 방향을 잡을 수 있다. C에 대한 대수학적 곡선도 마찬가지로 위상학적 차원 2를 가지고 있다; 다시 말하면 표면이다.

이 표면의 위상학 속, 즉 손잡이나 도넛 구멍의 수인 것은 대수학적 수단으로 계산할 수 있는 대수곡선의 기하학적 속과 같다. 요컨대, 도(d)를 가지고 있고 일반적인 특이점(타원성 2의 특이점)만 있는 비등성 곡선의 평면 투영을 고려한다면, 속은 (d - 1)(d - 2)/2 - k이며, 여기서 k는 이러한 특이점의 수입니다.

컴팩트 리만 표면

리만 표면은 하나의 복잡한 치수의 연결된 복합 분석 다지관으로, 2차원의 연결된 실제 다지관이 된다. 위상학적 공간으로서 콤팩트하면 콤팩트하다.

C에 대한 부드러운 비확산성 투영 대수 곡선 범주(비정규 정규 지도를 모피즘으로 함), 콤팩트 리만 표면 범주(비정규적인 홀로모르픽 지도를 모피즘으로 함), C에 대한 하나의 변수에서 대수 기능 필드 범주의 반대 범주(wit) 사이에 세 배의 등가 있다.c를 형태론으로 고정하는 h 필드 동형성). 이것은 이 세 과목을 공부하는 데 있어서 우리는 어떤 의미에서는 하나와 같은 것을 공부하고 있다는 것을 의미한다. 대수 기하학에서는 복잡한 분석법을, 복합 분석에서는 대수학-기하학 방법을, 양쪽에서는 현장-기하학 방법을 모두 사용할 수 있도록 한다. 이것은 대수 기하학에서 훨씬 더 광범위한 문제의 특징이다.

보다 일반적인 이론에 대해서는 대수 기하학 및 분석 기하학도 참조한다.

특이점

접선 공간의 내재적 개념을 사용하여 대수 곡선 C의 점 P는 평활(동음이의어: 비송음) 또는 단수(또는 단수)로 분류된다. n+1 변수의 n-1 동종 다항식을 고려할 때, Jacobian 행렬을 부분파생상품의 (n-1)×(n+1) 행렬로 찾을 수 있다. 이 행렬의 순위가 n-1이면 다항식은 대수 곡선을 정의한다(그렇지 않으면 그들은 더 높은 차원의 대수적 다양성을 정의한다). 자코비안 행렬이 곡선의 P 지점에서 평가될 때 순위가 n-1로 유지되면 점수는 평활점 또는 정규점이고, 그렇지 않으면 단수점이다. 특히 곡선이 단일 동종 다항 방정식 f(x,y,z) = 0으로 정의되는 평면 투영 대수 곡선이라면 단수점은 정확히 1×(n+1) 행렬의 순위가 0인 지점 P이다.

f는 다항식이기 때문에 이 정의는 순전히 대수학이며 필드 F의 성격에 대해서는 가정을 하지 않으며, 특히 실제 또는 복잡한 숫자가 될 필요는 없다. 물론 (0,0,0)은 곡선의 점이 아니므로 단수점이 아니라는 점을 상기해야 한다.

마찬가지로, 단일 다항식 f(x,y) = 0으로 정의된 아핀 대수곡선의 경우, 단수점은 정확히 1×n 자코비안 행렬의 순위가 0인 곡선의 점 P이다.

곡선의 특이점은 쌍생 불변성이 아니다. 그러나, 곡선의 특이점을 찾아 분류하는 것은 그 속을 계산하는 한 가지 방법인데, 그것은 쌍생불변량이다. 이를 위해서는 곡선을 투영적으로 고려해야 하며 F를 대수적으로 닫아 곡선에 속하는 모든 특이점이 고려되도록 해야 한다.

특이점 분류

단수점에는 곡선이 그 자체로 교차하는 여러 점, 예를 들어 등식³ x = y를² (0,0)에 있는 곡선으로 표시되는 다양한 유형의 정지가 포함된다.

C 원곡선은 기껏해야 한정된 수의 단수점을 가지고 있다. 만약 그것이 하나도 없다면, 그것은 부드러운 혹은 노래하지 않는 것으로 불릴 수 있다. 일반적으로, 이 정의는 대수적으로 닫힌 영역과 투영 공간의 곡선 C에 대해 이해된다(즉, 대수 기하학의 의미에서 완전). 예를 들어,${\displaystyle {}^{}}$ ${\displaystyle {y\mathrm{}}^{}}$ -$$x 3${\displaystyle {}^{}}$= ${\displaystyle 0}$ {\$displaystyle y-x^{3}=$0}의 평면 곡선은 무한대에 단수점(정점)을 갖는 것으로 간주된다$$.

이 조의 나머지 부분에서는 이바리테 다항식 f(x, y)의 영점 집합으로 정의된 평면 곡선 C를 고려한다. 전부는 아니지만 일부 결과는 비 평면 곡선으로 일반화될 수 있다.

단수점은 몇 가지 불변제를 이용하여 분류한다. 다중성 m은 최대 m – 1까지의 모든 주문에 대한 f의 파생상품이 소멸되는 최대 정수로 정의된다(또한 P에서 곡선과 직선 사이의 최소 교차로 번호). 직관적으로 단수점은 P에 Δ의 통상적인 이중점을 집중시키면 델타 불변성 Δ를 가진다. 이를 정밀하게 하기 위해 블로업 공정은 소위 무한 근접점을 생성하며, 무한 근접점에 대해 m(m-1)/2를 합하면 m이 이들의 다중성인 Δ가 생성된다. For an irreducible and reduced curve and a point P we can define δ algebraically as the length of ${\displaystyle {\widetilde {{\mathcal {O}}_{P}}}/{\mathcal {O}}_{P}}$ where ${\displaystyle {\mathcal {O}}_{P}}$ is the local ring at P and ${\displaystyle {\widetil$$de {{\mathcal{O}_{P}}}}}$은(는) 일체형 폐쇄다.^[1]

매핑의 특이점의 밀너 번호 μ를 .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em.반경 ε의 작은 구에 졸업생 f는( 복잡한)기울기 vect 연속적인 지도의 지형적 학위를 받은 의미에서}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}grad f(x, y)/ 대학원 f(x, y).아니면 필드의 f 그것은 밀너-중 공식에 의해 Δ와 r과 관련이 있다.

여기서 P의 지점 번호 r은 P에서 국소적으로 수정할 수 없는 지점의 수입니다. 예를 들어, r = 일반 첨점에서 1을, r = 2를 일반 이중 지점에서 2를 각각 사용한다. 다중성 m은 최소 r이고, 그 P는 최소 m이 2인 경우에만 단수다. 더욱이 Δ는 최소 m(m-1)/2이다.

모든 특이점의 델타 불변량을 계산하면 곡선의 속 g를 결정할 수 있다. 만약 d가 정도라면,

여기서 합계는 복합 투영 평면 곡선의 모든 단수점 P를 인수한다. 그것은 속 공식이라고 불린다.

불변성[m, Δ, r]을 특이성에 할당한다. 여기서 m은 다중성, Δ는 델타-상변성, r은 분기수다. 그 다음에 보통 첨점은 불변 [2,1,1]이 있는 점이고, 보통 이중점은 불변 [2,1,2]이 있는 점이며, 보통 m-복수점은 불변성 [m, m(m-1)/2, m]이 있는 점이다.

곡선의 예

이성곡선

단수 곡선이라고도 불리는 이성적 곡선은 합리적으로 선과 동등한 어떤 곡선을 의미하며, 이것은 우리가 투영적인 선으로 받아들일 수 있다. 따라서, 우리는 하나의 불확실한 F(x)에서 이성적 함수의 장을 가지고 곡선의 함수 필드를 식별할 수 있다. 만약 F가 대수적으로 닫힌다면, 이것은 속 0의 곡선에 해당하지만, 실제 대수적 다양성² x+y² = -1에 정의된 모든 실제 대수적 함수의 장은 합리적인 함수 분야가 아닌 속 0의 필드다.

구체적으로는 F에 걸쳐 치수 n의 부속 공간에 내장된 합리적 곡선은 단일 매개변수 t의 n 합리적 함수를 이용하여 매개변수화할 수 있다(단, 격리된 예외 지점 제외). 이러한 합리적 함수를 동일한 분모로 축소함으로써 n+1 결과 다항식은 투영적 컴플레의 다항식 파라메트리지를 정의한다.투영 공간에서의 곡선 구현 이 모든 다항식이 단항인 합리적 정규 곡선이 그 예다.

F에서 이성적인 점을 갖는 F에 대해 정의된 원뿔 부분은 합리적인 곡선이다. 합리적인 점을 통해 경사 t로 선을 그리고 평면 2차 곡선과의 교차점을 그려 매개변수를 지정할 수 있다. 이는 F-합리적 계수와 하나의 F-합리적 루트를 가진 다항식을 제공하므로 다른 루트도 F-합리적(즉, F에 속한다)이다.

예를 들어 타원 x² + xy + y² = 1을 고려하십시오. 여기서 (-1, 0)은 합리적인 지점입니다. (-1,0), y = t(x+1)에서 경사 t로 선을 긋고 타원 방정식으로 대체하여 x에 대한 인수 및 해결을 구한다.

그러면 y에 대한 방정식은

타원의 합리적인 매개변수화를 정의하여 타원이 합리적인 곡선임을 보여준다. t = ∞에 해당하는 (-1,1)를 제외하고 타원의 모든 점이 주어지며, 따라서 전체 곡선은 실제 투영 선에 의해 매개변수화된다.

그러한 합리적인 매개변수화는 첫 번째 투영 좌표를 매개변수화의 분자와 동일시하고 마지막 좌표를 공통분모에 동일시하여 투영공간에서 고려할 수 있다. 매개변수가 투영 선에서 정의되므로 매개변수의 다항식은 균질화되어야 한다. 예를 들어, 위의 타원의 투영 파라미터화는

이 방정식들 사이에서 T와 U를 제거하면 타원의 투영 방정식을 다시 얻을 수 있다.

위의 방정식을 균질화함으로써 쉽게 얻을 수 있다.

위키피디아의 곡선 목록에 있는 많은 곡선은 합리적이고 따라서 유사한 합리적 매개변수를 가지고 있다.

합리적인 평면 곡선

Rational plane curves are rational curves embedded into ${\displaystyle \mathbb {P} ^{2}}$. Given generic sections ${\displaystyle s_{1},s_{2},s_{3}\in \Gamma (\mathbb {P} ^{1},{\mathcal {O}}(d))}$ of degree ${\displaystyle d}$ homogeneous polynomials in two c좌표, ${\displaystyle x}$, y ${\displaystyle x,y$ 지도가 있다.

에 의해 주어지는. $도{\displaystyle }$ d$[\displaystyle d}$의 합리적인 평면 곡선 정의$.$^[2] There is an associated moduli space${\displaystyle {\mathcal {M}}={\overline {\mathcal {M}}}_{0,0}(\mathbb {P} ^{2},d\cdot [H])}$ (where ${\displaystyle [H]}$ is the hyperplane class) parametrizing all such stable curves. 치수 카운트는 모듈리 공간 치수를 결정하기 위해 만들 수 있다. $\gamma {\displaystyle \mathrm{}({\mathbb{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$,${\displaystyle {}^{}O}$(${\displaystyle }$d )${\displaystyle$ $d+1}$ 파라미터에는$$ 각 $섹션$에 대해 총 $3d{\displaystyle \mathrm{}}$ +${\displaystyle 3}$ ${\displaystyle$ 3d+$3} 파라미터$를 제공하는 d$$ +${\displaystyle 1}$ {\d$)$ {\displaystyle $\Gammatb {P} ^1,{\mathcal{O}}$ 파라미터가 있다$.$ 그런 다음 ${\displaystyle {\mathrm{}}^{}}$ $2{\displaystyle {\mathbb{}}^{}}$ ${\$ $M{\displaystyle \mathcal{}}$ ${\$에는 $1{\displaystyle \mathrm{}}$ ${\displaystyle 1}$개의$$ 매개 변수가 감소하고$,$ ${\displaystyle {\mathrm{}}^{}}$ P $1{\displaystyle {\mathbb{}}^{}}$ ${\$}의 3차원 자동화 그룹이 있으므로, $M{\displaystyle \mathcal{}}$$.${\displaystyle{{M\mathcal}}}이 치수 3d+3− 1− 3=3d− 1{3d+3-1-3=3d-1\displaystyle}. 이moduli 공간 될 수 있어 사용되는 것 수를 Nd{\displaystyle N_{d}}의 학위 d{\displaystyle d}합리적인 비행기 곡선을 교차하는 3d− 1{3d-1\displaystyle}포인트를 이용하는 Gromov–Witten 이론이다.[3] 그것은 재귀 관계에 의해 주어진다.여기서 $N{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle 2{}_{}}$= 1 ${\displaystyle N_{1}=N_{2}=1$

타원 곡선

타원곡선은 합리적인 점을 가진 속 1의 곡선으로 정의될 수 있다. 공통 모델은 비정규 입방곡선으로, 어떤 속이라도 하나의 곡선을 모형화하기에 충분하다. 이 모델에서 구분점은 일반적으로 무한대의 변곡점으로 간주된다. 이는 커브를 Tate-Weierstrass 형식으로 작성할 것을 요구하는 양이며, 이는 투영 버전에서 볼 수 있다.

필드의 특성이 2와 3과 다른 경우, 좌표의 선형 변경으로 1 =${\displaystyle {}_{}{a\mathrm{}}_{}}$ 2${\displaystyle {}_{}}$= ${\displaystyle {a\mathrm{}}_{}}$ ${\displaystyle {}_{}}$= $,$ {\$displaystyle a_{1}=a_{2}=a_{$3}=$0,}$을(를) 넣을 수 있으며, 이$$ 경우 고전적인 Weierstrass 형식이 제공된다.

타원곡선에는 그룹법의 정체성으로 구별되는 점을 가진 아벨 그룹의 구조가 실려 있다. 평면 입방형 모델에서 세 점은 일렬로 있는 경우에만 그룹에서 0을 합한다. 복잡한 숫자에 걸쳐 정의된 타원곡선의 경우, 그룹은 해당 타원함수의 주기 격자로 복잡한 평면의 첨가물 그룹에 이형화된다.

일반적으로 2개의 4중 표면의 교차점은 1과 4도의 비정형 곡선이며, 따라서 타원형 곡선이 이성적인 점을 갖는 경우이다. 특별한 경우, 교차점은 합리적인 단수 사분위수이거나 항상 구별되지 않는 작은 도(입방곡선과 선, 두 개의 원뿔, 원뿔과 두 개의 선 또는 네 개의 선)의 곡선으로 분해될 수 있다.

1개보다 큰 속곡선

1개보다 큰 속 곡선은 합리적 곡선과 타원형 곡선이 모두 현저하게 다르다. 팔팅스의 정리에 의해 이성적인 숫자에 걸쳐 정의되는 그러한 곡선은 오직 한정된 수의 이성적인 점만을 가질 수 있으며, 그것들은 쌍곡 기하학적 구조를 가진 것으로 볼 수도 있다. n이 3보다 클 경우 과페렐립트 곡선, 클라인 쿼트릭 곡선, 페르마트 곡선 xⁿ + y = z가ⁿⁿ 그 예다. 또한 P ${\displaystyle {\mathrm{}}^{}}$ ${\$의 투영 평면 곡선과 ${\displaystyle {}^{}}$ $1{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {\mathbb{}}^{}}$ ${\$ \$mathb$ {P}$$^1}{1}}}}{1}:{1$}}}}}}}}}}$의 곡선은 많은 유용한 예를 제공한다$$.

투영 평면 곡선

Plane curves ${\displaystyle C\subset \mathbb {P} ^{2}}$ of degree ${\displaystyle k}$, which can be constructed as the vanishing locus of a generic section ${\displaystyle s\in \Gamma (\mathbb {P} ^{2},{\mathcal {O}}(k))}$, has genus

그것은 Coistent sheaf cohomology를 사용하여 계산될 수 있다. 다음은 곡선의 정도에 대한 간략한 요약이다.예를$$ 들어, 곡선 ${\displaystyle {x\mathrm{}}^{}}$ 4${\displaystyle {}^{}}$+ ${\displaystyle {y\mathrm{}}^{}}$ 4${\displaystyle {}^{}}$+ ${\displaystyle {z\mathrm{}}^{}}$ ${\displaystyle {}^{}}$ ${\$$displaystyle$ x$^{4}+y^{4}+y^{4$$}{$4$}}}$은(는) 미분 $4{\displaystyle \mathrm{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$,${\displaystyle {}^{}}$4 ${\displaystyle \mathrm{y}}$ ${\displaystyle {3\mathrm{}}^{}}$ 4 ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$ ${\$은 곡선과 함께 공통 0이 없으므로$$ 매끄러운 $3$의 곡선을 정의한다$$. A non-example of a generic section is the curve ${\displaystyle x(x^{2}+y^{2}+z^{2})}$ which, by Bezouts theorem, should intersect at most ${\displaystyle 2}$ points, is the union of two rational curves ${\displaystyle C_{1}\cup C_{2}}$ intersecting at two points. 참고 ${\displaystyle {C\mathrm{}}_{}}$ $1{\displaystyle {}_{}}$ ${\$}는$$ x ${\displaystyle x}$의 소멸 위치, ${\displaystyle C_{}}$ $2{\displaystyle {}_{}}$ ${\$}}은 x ${\displaystyle {2\mathrm{}}^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\\\\$z$^\{$2}}. These can be found explicitly: a point lies in both if ${\displaystyle x=0}$. So the two solutions are the points ${\displaystyle [0:y:z]}$ such that ${\displaystyle y^{2}+z^{2}=0}$, which are ${\displaystyle [0:1:-1]}$ and ${\displaystyle [0$$:1:{\sqrt{-11}]}$.

투영 선 곱하기

Curve ${\displaystyle C\subset \mathbb {P} ^{1}\times \mathbb {P} ^{1}}$ given by the vanishing locus of ${\displaystyle s\in \Gamma (\mathbb {P} ^{1}\times \mathbb {P} ^{1},{\mathcal {O}}(a,b))}$, for ${\displaystyle a,b\geq 2}$, give curves of 속

Coistent sheaf cohomology를 사용하여 확인할 수 있다. $a{\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle a=2}$인 경우$,$ $그들$은 2${\displaystyle \mathrm{b}}$-${\displaystyle 2}$ -${\displaystyle \mathrm{b}}$ +${\displaystyle 1}$= ${\displaystyle \mathrm{b}}$- 1의 곡선을 정의하고$,$ 따라서 어떤 속이라도 ${\displaystyle {\mathrm{}}^{}}$ 1${\displaystyle {}^{}}$× ${\displaystyle {\mathrm{}}^{}}$$$${\displaystyle {\mathbb{}}^{}}$ ${\$1}$번 \mathb {P}$^1}$$$^$1}{1}{1}의 곡선으로 구성할 수 있다. 그들의 세대는 표에 요약될 수 있다.${\displaystyle \mathrm{및}}$ a${\displaystyle }$= 3 ${\displaystyle a=3}$의 경우$,$

참고 항목

고전 대수 기하학

현대 대수 기하학

리만 표면의 기하학적 구조

메모들

참조

위키미디어 커먼즈에는 대수곡선과 관련된 미디어가 있다.

• Brieskorn, Egbert; Knörrer, Horst (2013). Plane Algebraic Curves. Translated by Stillwell, John. Birkhäuser. ISBN 978-3-0348-5097-1.
• Chevalley, Claude (1951). Introduction to the Theory of Algebraic Functions of One Variable. Mathematical surveys. Vol. 6. American Mathematical Society. ISBN 978-0-8218-1506-9.
• Coolidge, Julian L. (2004) [1931]. A Treatise on Algebraic Plane Curves. Dover. ISBN 978-0-486-49576-7.
• Farkas, H. M.; Kra, I. (2012) [1980]. Riemann Surfaces. Graduate Texts in Mathematics. Vol. 71. Springer. ISBN 978-1-4684-9930-8.
• Fulton, William (1989). Algebraic Curves: An Introduction to Algebraic Geometry. Mathematics lecture note series. Vol. 30 (3rd ed.). Addison-Wesley. ISBN 978-0-201-51010-2.
• Gibson, C.G. (1998). Elementary Geometry of Algebraic Curves: An Undergraduate Introduction. Cambridge University Press. ISBN 978-0-521-64641-3.
• Griffiths, Phillip A. (1985). Introduction to Algebraic Curves. Translation of Mathematical Monographs. Vol. 70 (3rd ed.). American Mathematical Society. ISBN 9780821845370.
• Hartshorne, Robin (2013) [1977]. Algebraic Geometry. Graduate Texts in Mathematics. Vol. 52. Springer. ISBN 978-1-4757-3849-0.
• Iitaka, Shigeru (2011) [1982]. Algebraic Geometry: An Introduction to Birational Geometry of Algebraic Varieties. Graduate Texts in Mathematics. Vol. 76. Springer New York. ISBN 978-1-4613-8121-1.
• Milnor, John (1968). Singular Points of Complex Hypersurfaces. Princeton University Press. ISBN 0-691-08065-8.
• Serre, Jean-Pierre (2012) [1988]. Algebraic Groups and Class Fields. Graduate Texts in Mathematics. Vol. 117. Springer. ISBN 978-1-4612-1035-1.
• Kötter, Ernst (1887). "Grundzüge einer rein geometrischen Theorie der algebraischen ebenen Curven" [Fundamentals of a purely geometrical theory of algebraic plane curves]. Transactions of the Royal Academy of Berlin. — 1886년 아카데미 상을^[1] 받았다.