디스크(수학)

디스크:

둘레 C

직경 D

반지름 R

중심 또는 원점 O

기하학에서 디스크(디스크)^[1]는 원으로 둘러싸인 평면 내의 영역입니다.디스크는 경계를 구성하는 원이 포함되어 있으면 닫히고,^[2] 포함되지 않으면 열렸다고 한다.

$radius{\displaystyle }$r {\$displaystyle$$$$D_{r$}}의$$$$ 경우 $오픈디스크$는 보통 ${\displaystyle D_{}}$r 로, $클로즈드디스크$는 ${\displaystyle \stackrel{}{D_{}}}$ r${\displaystyle }$로 $표시$됩니다$(\$$displaystyle$${D_{$r$\}\}).$ 단$$, 토폴로지 필드에서는 오픈디스크는 ${\displaystyle {보통\mathrm{}}^{}}$ D 2$$로 ${\displaystyle {표시}^{}}$됩니다(\$displaystyle$ D$^{2$$}}).$$splaystyle \operatorname {Int} D^{2$

수식

데카르트 좌표에서 중심${\displaystyle }$(${\displaystyle a}$,${\displaystyle b}$) {$displaystyle (a, b)}$ 및$$ 반지름 R의 열린 원반은 다음 공식으로^[1] 표시됩니다.

$\displaystyle D=\{(x,y)\in {mathbb {R}:(x-a)^{2}+(y-b)^{2}<R^{2}\}$

같은 중심과 반지름의 닫힌 디스크는 다음과 같이 주어집니다.

${\displaystyle {D}=\{(x,y)\in {mathbb {R}^{2}+(y-b)^{2}\leq R^{2}\}.}$

반지름 R의 닫힌 디스크 또는 열린 디스크의 면적은 µR입니다²(디스크 ^[3]영역 참조).

특성.

디스크는 원형 ^[4]대칭입니다.

열린 디스크와 닫힌 디스크는 서로 다른 위상 특성을 가지고 있기 때문에 위상적으로 동일하지 않습니다(즉, 동형성이 아닙니다).예를 들어, 닫힌 모든 디스크는 압축되지만 열린 모든 디스크는 ^[5]압축되지 않습니다.그러나 대수적 위상학의 관점에서 그들은 많은 특성을 공유한다: 둘 다 수축^[6] 가능하고 단일 점에 해당하는 호모토피도 마찬가지이다.이는 기본 그룹이 사소하고 Z와 동형인 0번째 그룹을 제외한 모든 호몰로지 그룹이 사소하다는 것을 의미합니다.한 점의 오일러 특성(따라서 닫힌 원반 또는 열린 원반의 오일러 특성)은 ^[7]1입니다.

닫힌 디스크에서 그 자체로 이어지는 모든 지도는 하나 이상의 고정점을 가지고 있습니다(지도가 비사사적이거나 심지어 사사적일 필요는 없습니다). 이것이 브루어 고정점 ^[8]정리의 경우 n=2입니다.열려 있는 ^[9]디스크에 대해 다음 문장이 잘못되었습니다.

예를 들어 열린 장치 디스크의 모든 점을 열린 장치 디스크의 오른쪽에 있는 다른 점에 매핑하는 $함수{\displaystyle }$f (${\displaystyle x}$ ,${\displaystyle }$y ) ${\displaystyle =}$ (${\displaystyle \frac{}{}x\frac{}{}}$ +${\displaystyle \frac{\sqrt{}1\sqrt{\mathrm{}}}{}}$ - ${\displaystyle \frac{\sqrt{{}^{}}}{\mathrm{}}}$ 2${\displaystyle }$,${\displaystyle y}$) { $displaystyle$f ($x$ , $y$ ) = \ $left$\$frac${ x + { \ $light rt${ 1 - $^$ { 2$}}$ {2} $, y$ \ $right$} } } 를 생각해 보겠습니다$$.그러나 닫힌 장치 디스크의 경우 2 + 2 $=$, x>의모든 점을 수정합니다$.$ {\$display style$ x$^{2}+y^{2$}=$1,x>0$$}$

통계적 분포로서

디스크의 지점에서 위치까지의 평균 거리

단위 원형 디스크 상의 균일한 분포는 통계에서 가끔 볼 수 있습니다.이는 도시계획의 수학에서 운영연구에서 가장 흔하게 발생하며, 도시 내 인구 모델링에 사용될 수 있다.다른 용도는 주어진 일련의 선형 부등식이 충족될 확률을 계산하기 쉬운 분포라는 사실을 이용할 수 있다. (평면 내의 가우스 분포는 숫자 직교형이 필요하다.)

"초등 기능을 통해 한 독창적인 주장"두 지점 사이의 디스크의 유클리드 거리가 되.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output .s을 보여 준다.반면 극좌표의 직접적인 통합은 평균 제곱 거리 1을 보여 주Frac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output 0.90541,[10]≈ .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}128/45π.

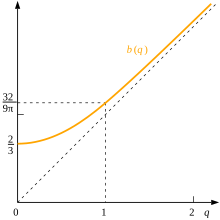
디스크 중심에서 거리 q에 임의의 위치가 주어진 경우 분포에서 이 위치까지의 평균 거리 b(q)와 해당 거리의 평균 제곱을 결정하는 것도 중요합니다.후자의 값은 q+1/2로 직접² 계산할 수 있습니다.

임의의 내부 지점까지의 평균 거리

디스크에서 내부 지점까지의 평균 거리

b(q)를 찾으려면 위치가 내부 또는 외부인 경우, 즉 q ≤ 1인 경우를 별도로 살펴볼 필요가 있으며, 두 경우 모두 완전한 타원 적분이라는 관점에서만 결과를 표현할 수 있음을 알 수 있다.

내부 위치를 고려할 경우, (도표에서) 목표는 0 µ r µ s(θ)에 대해 밀도가 1/µ인 분포에서 r의 기대값을 계산하는 것이며, 따라서 셀 면적이 r dr d µ인 고정 위치를 중심으로 한 극좌표로 적분하는 것이다.

$${\displaystyle b(q)=pi }}\int _{0}^2\pi }{\textrm {d}{s(\theta)}r^{2}{\textrm {d}r=pi}\int _0{2\ta}^{s}{s}{\textr}{{\textrcfrac {1}{\pi}{{{{{{{\pi}}}}}}}}}{{{\t}}}}}}}}}}}{s}}}}}$$

여기서 s())는 코사인 법칙을 사용하여 q와 θ로 구할 수 있다.적분을 평가하는 데 필요한 단계는 몇 가지 참조와 함께 Lew 등에 의해 논문에서 찾을 것이다.; 그 결과는 이다.^[10]

$${\displaystyle b(q)=bigfrac {4}{9\pi}}{\biggl \{}4(q^{2}-1)K(q^{2}+7)E(q^{2}){\biggr \}}$$

임의의 외부 지점까지의 평균 거리

디스크에서 외부 지점까지의 평균 거리

외부 로케이션으로 눈을 돌리면 비슷한 방법으로 적분을 셋업할 수 있으며, 이번에는

$${{displaystyle b(q)=bigfrac {2}{3\pi }}\int _{0}^{\textrm {sin}{\textfrac {1}{\tfrac {q}}{\biggl \{{}-s_{-}(\theta}){-s_{-{-}\textrm}}{textrm}}} {textrm}} {textrm} {textrm} {textrm}$$

$$\displaystyle s^{2}-2qs, {\textrm {cos}}\theta +q^{2}\!-\1=0.}$$

$${\displaystyle b(q)=pi }\int _{0}^{\textrm {sin}{-1}{\tfrac {1}{q}{\textrm {cos}{2}\textrm {1-q^2}{text}{ta}{{text}}{bgl \t}{\textrm{{{{{text}}}}}}{{{{{t}}}}}}{tfrac {t}}}}{{{t}}}}}}}}}}{$$

$${\displaystyle{\begin{정렬}(q)&, ={\frac{4}{3\pi}}\int _{0}^{1}{\biggl\와 같이{}3{\sqrt{q^{2}-u^{2}}}{\sqrt{1-u^{2}}}+{\frac{(1-u^{2})^{\tfrac{3}{2}}}{\sqrt{q^{2}-u^{2}}}}{\biggr)}}{\textrm{d}}u\\[0.6ex]&, ={\frac{4}{3\pi}}\int _{0}^{1}{\biggl\와 같이{}4{\sqrt{q^{2}-u^{2}}}{\sqrt{1-u^{2}}}-{\frac{{2q^}-1}{q}}{\frac{\sqrt{1-u^{2}}}{\sqr.t{q^{2}-u^{2}}}}{\biggr)}}{\textrm{d}}u\\[0.6ex]&, ={\frac{4}{3\pi}}{\biggl\와 같이{}{\frac{4q}{3}}{\biggl(}({2}+1q^)E({\tfrac{1}{{2}}q^})-(q^{2}))K({\tfrac{1}{{2}}q^}){\biggr)}(q^{2})){\biggl(}qE({\tfrac{1}{{2}}q^})-{\frac{{q^ 2}-1}{q}}K({\tfrac{1}{{2}}q^}){\biggr)}{\biggr)}}\\[0.6ex]&, ={\frac{4}{9\pi}}{\biggl\와 같이{}(q^{2}+7)E({\tfrac{1}.{q^{2}}})-{\frac {q^{2}-1}{q}}(q^{2}+3)K({\tfrac {1}{q^{2}}){\biggr \}\end {aligned}}})$$

따라서^[13] 다시 b(1) = 32/9µ이지만,

$$\displaystyle \lim _{q\to \infty }b(q)=q+{\tfrac {1}{8q}}.}$$

계산

완전한 타원 적분은 산술-기하 ^[14]평균의 방법으로 계산할 수 있습니다.그러면 b(q)는 다음 라인을 따라 코드에 의해 양호한 정확도로 결정될 수 있습니다.

  이중으로 하다 디스크(이중으로 하다 q)   { 이중으로 하다 x,a,b,c,구식,아다시,멀티,csum,K,KminusE,q,파이=3.141592653589793 ;      한다면(q==0) 돌아가다 2.0/3.0 ; 또 다른 q = 팹(q) ;     한다면(q==1) 돌아가다 32/(9*파이) ;     q = q * q ;      한다면(q< >1) x = q ; 또 다른 x = 1/q ;         // agm     b = sqrt(1-x) ;     c = sqrt(x) ;      위해서(a=1,구식=c+1,csum=c*c/2,멀티=1;c>1e-15& &c< >구식;csum+=멀티*c*c,멀티*=2)     { 구식 = c ; c = (a-b)/2 ; 아다시 = (a+b)/2 ; b = sqrt(a*b) ; a = 아다시 ; }     K = 파이 / (2*a) ;     KminusE = K * csum ;         한다면(q< >1) 돌아가다 (4/(9*파이)) * ((5*q+3)*K   - (q+7)*KminusE) ;     또 다른    돌아가다 (4/(9*파이)) * ((5*q+3)*K/q - (q+7)*KminusE*q) ;   } 

「 」를 참조해 주세요.

• 유닛 디스크, RADIUS 1의 디스크
• 두 개의 동심원 사이의 영역인 환상(수학)
• 볼(수학), 디스크의 3차원 유사체를 나타내는 일반적인 용어
• 디스크 대수, 디스크의 함수 공간
• 디스크 세그먼트
• 삼각형의 특정 중심을 포함하는 직교 중심 디스크

레퍼런스