콘웨이의 삶의 게임

Conway's Game of Life
"Conway game"이 여기로 리디렉션됩니다. 콘웨이의 초현실적 숫자 게임 이론은 초현실적 숫자를 참조하세요.
고스퍼의 글라이더 건 하나로 글라이더 제작
후미에 글라이더 총(초록색)을 남기는 퍼퍼형 사육사(빨간색)의 스크린샷(애니메이션)

간단히 생명이라고도 알려진 생명의 게임은 1970년 영국 수학자 존 호튼 콘웨이가 고안한 세포 자동화 장치입니다.[1] 제로 플레이어 게임으로 초기 상태에 따라 진화가 결정되어 더 이상의 입력이 필요하지 않습니다.[2][3] 초기 구성을 만들고 어떻게 진화하는지 관찰함으로써 생명의 게임과 상호 작용합니다. 튜링 완전하고 범용 컨스트럭터 또는 다른 튜링 기계를 시뮬레이션할 수 있습니다.

규칙.

생명의 게임의 우주는 무한히 2차원 직교하는 사각형 세포의 격자로, 각각 살아있거나 죽어있거나(또는 사람이 사는 상태와 사람이 사는 상태) 두 가지 가능한 상태 중 하나에 있습니다. 모든 세포는 수평, 수직 또는 대각선으로 인접한 세포인 8개의 이웃과 상호 작용합니다. 각 단계에서 다음과 같은 전환이 발생합니다.

  1. 살아있는 이웃이 2개 미만인 살아있는 세포는 마치 인구가 부족한 것처럼 죽습니다.
  2. 2개 또는 3개의 살아있는 이웃이 있는 살아있는 세포는 다음 세대에 걸쳐 살아갑니다.
  3. 3개 이상의 살아있는 이웃이 있는 살아있는 세포는 마치 인구 과잉인 것처럼 죽습니다.
  4. 정확히 3개의 살아있는 이웃을 가진 죽은 세포는 마치 생식에 의한 것처럼 살아있는 세포가 됩니다.

초기 패턴은 시스템의 시드를 구성합니다. 1세대는 살아있든 죽든 씨앗의 모든 세포에 위의 규칙을 동시에 적용하여 탄생합니다. 출생과 사망은 동시에 일어나는데, 이런 일이 일어나는 이산적인 순간을 진드기라고 부르기도 합니다.[nb 1] 각 세대는 이전 세대의 순수한 기능입니다. 규칙은 계속 반복적으로 적용되어 더 많은 세대를 만듭니다.

오리진스

Stanislaw Ulam은 1940년대에 Los Alamos National Laboratory에서 일하면서 간단한 격자 네트워크를 모델로 사용하여 결정의 성장을 연구했습니다.[7] 동시에 로스앨러모스에 있는 울람의 동료인 존 폰 노이만은 자기 복제 시스템의 문제를 연구하고 있었습니다.[8]: 1 폰 노이만의 초기 설계는 한 로봇이 또 다른 로봇을 만드는 아이디어를 바탕으로 이루어졌습니다. 이 디자인은 운동학적 모델로 알려져 있습니다.[9][10] 이 디자인을 개발하면서 폰 노이만은 자기 복제 로봇을 만드는 것의 큰 어려움과 복제 로봇을 만드는 데 드는 "부품의 바다"를 제공하는 데 드는 큰 비용을 깨닫게 되었습니다. 노이만은 1948년 힉슨 심포지엄을 위해 "오토마타의 일반적이고 논리적인 이론"이라는 제목의 논문을 썼습니다.[8]: 1 Ulam은 자기 복제의 환원주의 모델을 만들기 위해 이산 시스템을 사용할 것을 제안한 사람이었습니다.[8]: 3 [11]: xxix 울람과 폰 노이만은 1950년대 후반에 액체 운동을 계산하는 방법을 개발했습니다. 이 방법의 구동 개념은 액체를 이산 단위의 그룹으로 간주하고 이웃의 행동을 기반으로 각각의 움직임을 계산하는 것이었습니다.[12]: 8 그래서 세포 자동화의 첫 번째 시스템이 탄생했습니다. 폰 노이만의 셀룰러 오토마타는 울람의 격자 네트워크와 마찬가지로 2차원이며, 그의 자기 복제기는 알고리즘적으로 구현됩니다. 그 결과 작은 이웃을 가진 세포 자동화 장치 내에서 작동하는 범용 복사기 및 구성자(접촉하는 세포만 이웃이고 폰 노이만의 세포 자동화 장치의 경우 직교 세포만 해당)가 셀당 29개의 상태를 가지고 있었습니다. 폰 노이만은 특정 패턴이 주어진 세포 우주 안에서 자신을 끝없이 복제할 수 있다는 존재 증거를 제시했습니다. 이 설계는 테셀레이션 모델로 알려져 있으며, 폰 노이만 범용 구축기라고 합니다.[13]

수학적 논리의 질문과 울람의 시뮬레이션 게임에 대한 연구 등에 동기를 부여받은 존 콘웨이는 1968년에 다양한 2차원 세포 자동화 규칙으로 실험을 시작했습니다. 콘웨이의 초기 목표는 흥미롭고 예측 불가능한 세포 자동화를 정의하는 것이었습니다.[3] 마틴 가드너(Martin Gardner)에 따르면 콘웨이(Conway)는 패턴이 제한 없이 "분명히" 성장할 수 있도록 하는 규칙을 목표로 다양한 규칙을 실험하고, 주어진 패턴이 그렇게 한다는 것을 증명하는 것은 어렵습니다. 또한 일부 "단순한 초기 패턴"은 정적 구성 또는 반복 루프로 정착하기 전에 "상당 기간 동안 성장 및 변화"되어야 합니다.[1] 콘웨이는 나중에 라이프의 기본적인 동기는 "보편적인" 세포 자동화 장치를 만드는 것이라고 썼습니다.[14][better source needed]

이 게임은 1970년 10월 사이언티픽 아메리칸호에 처음으로 공개되었는데, 이 칼럼은 콘웨이와의 개인적인 대화를 바탕으로 한 마틴 가드너의 "수학 게임" 칼럼에 실렸습니다. 이론적으로, 생명의 게임은 보편적인 튜링 기계의 힘을 가지고 있습니다: 알고리즘적으로 계산될 수 있는 모든 것은 생명의 게임 내에서 계산될 수 있습니다.[15][2] 가드너(Gardner)는 "생명체 사회의 상승, 하락 및 변화에 대한 라이프의 유사성 때문에 '시뮬레이션 게임'(실생활 과정을 닮은 게임)이라고 불리는 것의 증가하는 계층에 속합니다."[1]라고 썼습니다.

게임 오브 라이프는 출판 이후 패턴이 진화할 수 있는 놀라운 방법 때문에 많은 관심을 끌었습니다. 출현과 자기 조직화의 예를 제공합니다.[3] 임의의 변동을 통합하는 생명체 버전은 물리학에서 상전이와 비평형 동역학을 연구하는 데 사용되었습니다.[16] 이 게임은 디자이너가 없을 때 디자인과 조직이 자발적으로 나타날 수 있다는 다소 반직관적인 생각을 전달하는 데 사용되는 교훈적인 비유의 역할도 할 수 있습니다. 예를 들어, 철학자 다니엘 데넷(Daniel Dennett)은 생명의 게임 "우주"의 비유를 광범위하게 사용하여 우리 우주를 지배할 수 있는 비교적 단순한 결정론적 물리 법칙 세트로부터 의식과 자유 의지와 같은 복잡한 철학적 구성의 가능한 진화를 설명했습니다.[17][18][19]

생명의 게임의 인기는 점점 더 저렴한 컴퓨터 접속과 동시에 생겨났기 때문에 도움이 되었습니다. 게임은 이 기계에서 몇 시간 동안 실행될 수 있으며, 그렇지 않으면 밤에도 사용되지 않은 채로 남아 있을 수 있습니다. 이런 점에서 컴퓨터로 만든 프랙탈의 후대 인기를 예고했습니다. 많은 사람들에게 Game of Life는 단순한 프로그래밍 과제였습니다. 그렇지 않으면 낭비되는 CPU 사이클을 재미있게 사용할 수 있는 방법이었습니다. 그러나 어떤 이들에게는 삶의 게임이 더 철학적인 의미를 내포하고 있었습니다. 1970년대와 그 이후에 컬트적인 추종자들을 발전시켰습니다. 현재의 발전은 게임 오브 라이프 보드의 범위 내에서 컴퓨터 시스템의 이론적 시뮬레이션을 만드는 데까지 나아갔습니다.[20][21]

패턴의 예

게임 오브 라이프에서는 행동에 따라 분류되는 다양한 유형의 패턴이 많이 발생합니다. 일반적인 패턴 유형에는 한 세대에서 다음 세대로 변하지 않는 정물체, 유한한 세대가 지나면 초기 상태로 돌아가는 오실레이터, 그리드를 가로질러 스스로 변환하는 우주선 등이 있습니다.

생명의 게임에서 가장 초기의 흥미로운 패턴은 컴퓨터를 사용하지 않고 발견되었습니다. 가장 간단한 정물화와 진동자는 바둑에서 사용하는 것과 같은 그래프 용지, 칠판, 물리 게임판 등을 이용하여 다양한 작은 출발 구성의 운명을 추적하는 과정에서 발견되었습니다. 이 초기 연구에서 콘웨이는 R-펜토미노가 소수의 세대에서 안정화에 실패했다는 것을 발견했습니다. 사실, 안정화되기 위해서는 1103세대가 필요한데, 그 때까지 116명의 개체수를 가지고 있고 6개의 탈출하는 글라이더를 만들어냈습니다;[22] 이것들은 지금까지 발견된 최초의 우주선들이었습니다.[23]

앞서 언급한 세 가지 패턴 유형의 자주 발생하는[24][25] 예(세포의 무작위 시작 구성에서 자주 발생한다는 점에서)를 보여주며, 살아있는 세포는 흰색으로 표시됩니다. 주기는 패턴이 초기 구성으로 돌아가기 전에 반복해야 하는 틱 수를 나타냅니다.

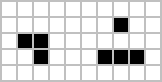
펄서는[26] 가장 일반적인 주기 3 발진기입니다. 자연적으로 발생하는 대부분의 진동자는 깜박임이나 두꺼비처럼 주기가 2이지만 모든 주기의 진동자가 존재하는 것으로 알려져 [27][28]있으며 주기 4, 8, 14, 15, 30 등의 진동자는 무작위 초기 조건에서 발생하는 것으로 나타났습니다.[29] 안정화되기 전에 오랜 기간 동안 진화하는 패턴은 메투셀라라고 불리는데, 그 중 최초로 발견된 것이 R-펜토미노입니다. 다이하드는 130세대가 지나면 안정화되기는커녕 결국 사라지는 패턴으로, 7개 이하의 세포로 패턴을 시작하는 데 최대가 될 것으로 추측됩니다.[30] 도토리는 탈출 글라이더 13개를 포함하여 633개의 세포를 생성하는 데 5,206세대가 필요합니다.[31]

R펜토미노
다이하드
도토리

Conway는 원래 어떤 패턴도 무한히 성장할 수 없다고 가정했습니다. 즉, 유한한 수의 살아있는 세포를 가진 초기 구성에 대해 개체군이 유한한 상한을 초과하여 성장할 수 없다고 가정했습니다. 《수학 게임》에 처음 등장한 콘웨이는 1970년이 끝나기 전에 추측을 증명하거나 반증할 수 있는 사람에게 50달러(2022년 380달러 상당)의 상금을 제공했습니다. 이 상은 11월에 빌 고스퍼가 이끄는 매사추세츠 공과대학교 팀에 의해 수상되었습니다; "고스퍼 글라이더 건"은 15세대에 첫 번째 글라이더를 생산하고, 그 이후로 30세대마다 또 다른 글라이더를 생산합니다. 수년 동안, 이 글라이더 건은 알려진 것 중 가장 작았습니다.[32] 2015년, 120세대마다 글라이더를 발사하는 "심킨 글라이더 건"이라고 불리는 총이 발견되었는데, 이것은 살아있는 세포는 적지만 끝에 있는 더 큰 경계 상자를 가로질러 펼쳐져 있습니다.[33]

고스퍼글라이더건
심킨글라이더건

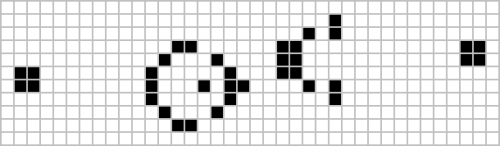나중에 무한한 성장을 보여주는 더 작은 패턴들이 발견되었습니다. 아래에 표시된 세 가지 패턴 모두 무한히 성장합니다. 처음 두 개의 블록은 하나의 블록 배치 스위치 엔진을 만듭니다: 게임의 우주를 가로질러 자신을 변환할 때 2 x 2개의 정지된 블록을 남기는 구성입니다.[34] 세 번째 구성은 두 개의 그러한 패턴을 만듭니다. 첫 번째 세포는 10개의 살아있는 세포만 가지고 있으며, 이는 최소인 것으로 입증되었습니다.[35] 두 번째는 5x5 정사각형에 맞고 세 번째는 1셀 높이에 불과합니다.


나중에 발견된 것들에는 정지해 있고 글라이더나 다른 우주선을 생산하는 다른 총들, 잔해의 흔적을 남기고 이동하는 퍼프 트레인, 그리고 이동하고 우주선을 배출하는 레이크가 포함되었습니다.[36] Gosper는 또한 점근적으로 최적의 2차 증식률을 가진 첫 번째 패턴을 구축했는데, 이 패턴은 일련의 총을 남겨두면서 작동했습니다.

글라이더가 다른 물체와 흥미로운 방식으로 상호 작용하는 것이 가능합니다. 예를 들어, 두 개의 글라이더가 특정 위치의 블록을 향해 발사되면, 그 블록은 글라이더의 소스에 더 가까이 이동합니다. 글라이더 3개를 딱 맞는 방법으로 쏘면 블록이 더 멀리 이동합니다. 이 슬라이딩 블록 메모리는 카운터 시뮬레이션에 사용할 수 있습니다. 글라이더를 이용하여 AND, OR, NOT 등의 논리 게이트를 구성할 수 있습니다. 두 개의 카운터에 연결된 유한 상태 기계와 같은 역할을 하는 패턴을 구축할 수 있습니다. 이것은 보편적인 튜링 기계와 같은 연산력을 가지고 있어서, 생명의 게임은 이론적으로 메모리가 무제한이고 시간의 제약이 없는 어떤 컴퓨터처럼 강력합니다. 이것은 튜링 완전한 것입니다.[15][2] 실제로 게임 오브 라이프에는 테트리스를 시뮬레이션하는 패턴을 포함하여 여러 가지 프로그래밍 가능한 컴퓨터 아키텍처가[37][38] 구현되었습니다.[39]

또한 패턴은 원래 패턴의 복사본을 포함하여 새로운 물체를 구성하는 방식으로 글라이더를 발사하는 총을 포함할 수 있습니다. 튜링 완전한 컴퓨터를 포함하고 더 많은 종류의 복잡한 물체를 만들 수 있는 범용 컨스트럭터를 만들 수 있습니다.[2]

2018년, 아담 P에 의해 최초의 진정한 초보적인 기사 작위인 Sir Robin이 발견되었습니다. 고우처.[40] 기사선은 수직으로 또는 45° 대각선을 따라 움직이는 것이 아니라 (체스의 기사처럼) 아래로 이동할 때마다 남아있는 두 개의 사각형을 움직이는 우주선입니다. 이는 48년 만에 발견된 초소형 우주선의 새로운 우주선 이동 패턴입니다. "초등"은 글라이더나 정물과 같은 더 작은 상호작용 패턴으로 분해될 수 없다는 것을 의미합니다.[41]

미확정성

생명의 게임의 많은 패턴들은 결국 정물화, 진동자 그리고 우주선의 조합이 됩니다; 다른 패턴들은 혼돈이라고 불릴 수 있습니다. 패턴은 결국 그러한 조합으로 정착할 때까지 매우 오랫동안 혼란 상태를 유지할 수 있습니다.

생명의 게임은 결정할 수 없습니다. 즉, 초기 패턴과 이후 패턴을 고려할 때 이후 패턴이 나타날지 여부를 알 수 있는 알고리즘이 존재하지 않습니다. 생명의 게임이 튜링 완전한 것을 감안할 때, 이것은 정지 문제의 결과입니다: 주어진 프로그램이 실행을 끝낼 것인지 아니면 처음 입력에서 영원히 실행을 계속할 것인지를 결정하는 문제입니다.[2]

비스듬한 우주선

베를레캄프는 1982년부터 기사처럼 움직이는 움직이는 패턴의 존재를 예측했지만, 2010년대까지만 해도 알려진 모든 우주선은 수직이나 대각선으로만 움직일 수 있었습니다. 수직도 대각선도 아닌 수직도 아닌 이동하는 우주선을 일반적으로 비스듬한 우주선이라고[42][43] 합니다. 2010년 5월 18일, 앤드류 J. 웨이드(Andrew J. Wade)는 "제미니(Gemini)"라는 이름의 첫 비스듬한 우주선을 발표했는데, 이는 모체를 파괴하면서 (5,1) 더 멀리에서 자신의 복사본을 만들어냅니다.[44][43] 이 패턴은 3,400만 세대에 걸쳐 복제되며, 채프먼-그린 구조 암으로 만들어진 두 개의 안정적인 구성 사이에서 진동하는 글라이더로 만들어진 지시 테이프를 사용합니다. 다시 패턴의 새 복사본을 만들고 이전 복사본을 파괴합니다. 2015년 12월, 쌍둥이자리의 대각선 버전이 만들어졌습니다.[45]

자기복제

2013년 11월 23일, Dave Green은 Game of Life에서 처음으로 지시 테이프를 포함한 전체 복사본을 만드는 복제기를 만들었습니다.[46] 2018년 10월 아담 P. Goucher는 자가 복제가 가능한 메타셀인 0E0P 메타셀의 제작을 마쳤습니다. 이는 Bris Due의 OTCA 메타픽셀과 같은 이전의 메타셀과는 달랐는데, 이는 이미 근처에 구축된 복사본에서만 작동했습니다. 0E0P 메타셀은 구성 암을 사용하여 프로그래밍된 규칙을 시뮬레이션하는 복사본을 생성함으로써 작동합니다.[47] 생명의 게임 또는 다른 무어 이웃 규칙의 실제 시뮬레이션은 더 많은 상태를 가진 폰 노이만 이웃을 사용하여 동등한 규칙을 시뮬레이션함으로써 수행됩니다.[48] 0E0P라는 이름은 "Zero Encoded by Zero Population"의 줄임말로, 메타셀이 빈 공간을 시뮬레이션하는 "오프" 상태에 있는 대신 0E0P 메타셀이 해당 상태에 들어가면 스스로 제거되어 빈 공간을 남깁니다.[49]

반복

그리드에 있는 대부분의 무작위적인 살아있는 세포의 초기 패턴에서 관찰자들은 세대가 지나갈 때 개체수가 계속 변하는 것을 발견할 것입니다. 단순한 규칙에서 나오는 패턴은 수학적 아름다움의 한 형태로 여겨질 수 있습니다. 초기 대칭이 없는 작은 고립된 부분 패턴은 대칭이 되는 경향이 있습니다. 일단 이런 일이 일어나면 대칭성이 풍부해질 수 있지만, 가까운 부분 패턴이 그것을 방해할 만큼 가까이 오지 않는 한 대칭성을 잃을 수 없습니다. 극히 일부의 경우, 사회는 결국 소멸되고 모든 살아있는 세포가 사라집니다. 하지만 이것은 많은 세대 동안 일어나지 않을 수도 있습니다. 대부분의 초기 패턴은 결국 다 소모되어 두 개 이상의 상태 사이에서 영원히 진동하는 안정적인 모양이나 패턴을 만들어냅니다.[50][51] 또한 많은 패턴은 하나 이상의 글라이더나 처음 위치에서 무한히 떨어진 곳을 이동하는 우주선을 만들어냅니다. 가장 가까운 이웃에 기반을 둔 규칙 때문에 단위 시간당 1셀 이상의 속도로 그리드를 통과하는 정보는 없습니다. 따라서 이 속도를 빛의 세포 자동 속도라고 하며 c로 표시합니다.

알고리즘

R-펜토미노와 같이 미래를 알 수 없는 초기 패턴은 컴퓨터 프로그래머들로 하여금 게임 오브 라이프에서 패턴의 진화를 추적하기 위한 프로그램을 작성하도록 이끌었습니다. 초기 알고리즘의 대부분은 유사했습니다. 컴퓨터 메모리에서 패턴을 2차원 배열로 나타냈습니다. 일반적으로 현재 세대를 유지하기 위한 어레이와 후속 세대를 계산하기 위한 어레이의 두 가지가 사용됩니다. 종종 0과 1은 각각 죽은 세포와 살아있는 세포를 나타냅니다. 중첩 루프는 현재 배열의 각 요소를 차례로 고려하여 각 셀의 살아있는 이웃을 계산하여 후속 배열의 해당 요소를 0 또는 1로 결정합니다. successor array(후계 배열)가 표시됩니다. 다음 반복을 위해, 어레이들은 마지막 반복에서의 후속 어레이가 다음 반복에서 현재 어레이가 되도록 역할들을 스왑할 수도 있고, 또는 하나는 제2 어레이의 값들을 제1 어레이에 복사한 후 제1 어레이로부터 제2 어레이를 다시 업데이트할 수도 있습니다.

이 기본 계획에 대한 다양한 사소한 향상이 가능하며 불필요한 계산을 절약할 수 있는 많은 방법이 있습니다. 마지막 시간 단계에서 변경되지 않고 이웃이 변경되지 않은 셀은 현재 시간 단계에서도 변경되지 않도록 보장하므로 활성화된 영역을 추적하는 프로그램은 비활성화된 영역을 업데이트하지 않음으로써 시간을 절약할 수 있습니다.[52]

Game of Life on the surface of a trefoil knot
토로이드 삼엽매듭 표면의 생명의 게임

계산 루프에서 결정과 분기를 피하기 위해 규칙은 이웃에 대한 내부 필드의 자기 중심적 접근 방식에서 과학적 관찰자의 관점으로 재배열될 수 있습니다: 주어진 이웃에 있는 모든 9개 필드의 합이 3이면 다음 세대의 내부 필드 상태는 생명이 될 것입니다. 모든 필드의 합이 4이면, 내부 필드는 현재 상태를 유지하고, 다른 모든 합은 내부 필드를 죽음으로 만듭니다.

메모리를 절약하기 위해 스토리지를 어레이 1개와 라인 버퍼 2개로 줄일 수 있습니다. 하나의 라인 버퍼를 사용하여 라인의 후속 상태를 계산한 다음 두 번째 라인 버퍼를 사용하여 다음 라인의 후속 상태를 계산합니다. 그런 다음 첫 번째 버퍼가 해당 행에 기록되고 세 번째 행에 대한 후속 상태를 유지하도록 자유로워집니다. 토로이드 배열을 사용하는 경우 마지막 줄이 계산될 때까지 배열의 첫 번째 줄의 원래 상태를 저장할 수 있도록 세 번째 버퍼가 필요합니다.

토로이드 배열의 글라이더 건. 글라이더의 물줄기는 결국 총을 감싸고 파괴합니다.
주기적 경계조건을 가지는 사각격자의 적색글라이더

생명의 게임 분야는 원칙적으로 무한대이지만 컴퓨터는 유한한 메모리를 가지고 있습니다. 이로 인해 활성 영역이 배열의 경계를 침범할 때 문제가 발생합니다. 프로그래머들은 이러한 문제를 해결하기 위해 여러 전략을 사용했습니다. 가장 간단한 방법은 어레이 외부의 모든 셀이 죽었다고 가정하는 것입니다. 이는 프로그래밍하기 쉽지만 활성 영역이 경계를 넘을 때 부정확한 결과로 이어집니다. 더 정교한 트릭은 필드의 왼쪽 및 오른쪽 가장자리와 위쪽 및 아래쪽 가장자리를 함께 연결하여 토로이드 배열을 생성하는 것을 고려하는 것입니다. 결과적으로 필드 가장자리를 가로질러 이동하는 활성 영역이 반대쪽 가장자리에서 다시 나타납니다. 패턴이 너무 커지면 여전히 부정확해질 수 있지만 병리학적 에지 효과는 없습니다. 동적 스토리지 할당 기술을 사용하여 증가하는 패턴을 유지하기 위해 훨씬 더 큰 어레이를 생성할 수도 있습니다. 유한장에서의 생명의 게임은 때때로 명시적으로 연구됩니다. 골리와 같은 일부 구현은 표준 무한장, 1차원에서만 무한장을 선택하거나 원통, 토러스 또는 뫼비우스 띠와 같은 위상 선택을 통해 유한장을 선택할 수 있습니다.

또는 프로그래머는 게임 오브 라이프 필드를 2차원 배열로 나타내는 개념을 버리고 살아있는 세포를 나타내는 좌표 쌍의 벡터와 같은 다른 데이터 구조를 사용할 수 있습니다. 이렇게 하면 모집단이 실시간 좌표 배열의 크기를 초과하지 않는 한 패턴이 방해받지 않고 필드를 이동할 수 있습니다. 단점은 살아있는 이웃을 세는 것이 해시 테이블 검색 작업이 되어 시뮬레이션 속도가 느려진다는 것입니다. 보다 정교한 데이터 구조를 통해 이 문제도 크게 해결할 수 있습니다.[citation needed]

큰 시간 깊이에서 큰 패턴을 탐색하는 경우 해시라이프와 같은 정교한 알고리즘이 유용할 수 있습니다. 또한 동기식 게임의 동작을 정확하게 모방하면서 임의의 비동기식 업데이트를 사용하여 Game of Life 및 기타 셀룰러 오토마타를 구현하는 방법도 있습니다.[53] 기본 Game of Life 시나리오를 C, C++, 자바, 파이썬 등 다양한 프로그래밍 언어로 구현한 소스코드 예시는 로제타코드에서 확인할 수 있습니다.[54]

변주곡

메인 기사: 생명체와 같은 세포 자동화 장치

생명의 게임이 시작된 이래로 새롭고 유사한 셀룰러 오토마타가 개발되었습니다. 표준 Game of Life는 규칙 문자열 표기법으로 B3/S23으로 기호화됩니다. 세포는 정확히 세 개의 이웃이 있으면 태어나고, 두 세 개의 살아있는 이웃이 있으면 살아남고, 그렇지 않으면 죽게 됩니다. 첫 번째 숫자, 즉 숫자 목록은 죽은 세포가 태어나기 위해 필요한 것입니다. 두 번째 세트는 다음 세대에 생존하기 위한 살아있는 세포의 요구 사항입니다. 따라서 B6/S16은 "6개의 이웃이 있으면 세포가 태어나고, 1개 또는 6개의 이웃이 있으면 살아간다"는 것을 의미합니다. 이러한 방식으로 설명할 수 있는 2차원 그리드 상의 셀룰러 오토마타를 생명과 같은 셀룰러 오토마타라고 합니다. 또 다른 일반적인 생명과 같은 오토마톤인 하이라이프(Highlife)는 규칙 B36/S23에 의해 설명되는데, 이는 원래 게임의 B3/S23 규칙 외에 6개의 이웃이 있으면 출산이 일어나기 때문입니다. 하이라이프는 자주 발생하는 복제기로 가장 잘 알려져 있습니다.[55][56]

생명체와 같은 추가적인 셀룰러 오토마타가 존재합니다. 이 두18 가지 다른[57] 규칙의 대다수는 너무 혼란스럽거나 너무 황량해서 관심을 끌 수 없는 우주를 생성하지만, 큰 부분집합은 흥미로운 행동을 보여줍니다. 추가적인 일반화는 등방성 규칙 공간을 생성하며, 두 가지102 가능한 세포 자동화 규칙[58](다시 생명의 게임)이 그 중 하나입니다. 이 규칙들은 생명체와 같은 규칙과 동일한 정사각형 격자와 동일한 8셀 이웃을 사용하며, 마찬가지로 회전과 반사 하에서도 불변합니다. 그러나 등방성 규칙에서는 인접한 셀의 총 개수뿐만 아니라 서로 상대적인 인접 셀의 위치를 고려하여 셀의 미래 상태를 결정할 수 있습니다.

2차원 육각형 Game of Life(규칙 H:B2/S34)의 2단계 발진기 및 4단계 발진기와 함께 48단계 발진기의 샘플

생명의 게임의 일부 변형은 규칙뿐만 아니라 우주의 기하학을 수정합니다. 위의 변형은 2차원 사각형으로 생각할 수 있는데, 세계는 2차원이고 사각형 격자로 배치되어 있기 때문입니다. 기본 세포 오토마타로 알려진 1차원 사각형 변형과 3차원 사각형 변형,[59] 그리고 2차원 육각형 및 삼각형 변형이 개발되었습니다. 비주기적 타일링 그리드를 사용한 변형도 만들어졌습니다.[60]

콘웨이의 규칙은 살아있는 주와 죽은 주 두 개가 아닌 세 개 이상이 되도록 일반화될 수도 있습니다. 그런 다음 상태 전환은 가중치 시스템 또는 각 상태에 대한 별도의 전환 규칙을 지정하는 표에 의해 결정됩니다. 예를 들어, Mirek's Cellebration의 다중 색상 규칙 표 및 가중 수명 규칙 패밀리에는 각각 생명의 게임과 동등한 샘플 규칙이 포함됩니다.

프랙탈 및 프랙탈 시스템과 관련된 패턴은 특정 생명체와 유사한 변형에서도 관찰될 수 있습니다. 예를 들어, 오토마톤 B1/S12는 단일 라이브 셀에 적용될 때 시에르핀스키 삼각형에 4개의 매우 가까운 근사치를 생성합니다. 시에르핀스키 삼각형은 또한 살아있는 세포들의 무한히 긴 단세포 두께의 라인의 장기적인 성장을 관찰함으로써 생명의 게임에서 관찰될 수 있고,[61] 하이라이프, 씨즈(B2/S), 울프람의 규칙 90에서도 관찰될 수 있습니다.[62]

이민은 게임 오브 라이프와 매우 유사한 변형이지만, 두 개의 주(州)가 있으며 종종 두 가지 다른 색상으로 표현됩니다. 새로운 세포가 탄생할 때마다, 그것은 그것을 낳은 세 개의 세포에서 가장 많은 온 상태를 띨 것입니다. 이 기능을 사용하여 우주선과 게임 내의 다른 물체 간의 상호 작용을 조사할 수 있습니다.[63] QuadLife라고 불리는 또 다른 유사한 변형은 4개의 서로 다른 상태를 포함합니다. 이웃의 세 가지 다른 세포에서 새로운 세포가 탄생할 때 네 번째 값을 취하며, 그렇지 않으면 이민처럼 다수의 값을 취합니다.[64] 온 셀 간의 변화를 제외하고 이 두 가지 변화는 모두 생명의 게임과 동일하게 작용합니다.

음악

다양한 음악 작곡 기법은 특히 MIDI 시퀀싱에서 Game of Life를 사용합니다.[65] 생명의 게임에서 생성된 패턴에서 소리를 생성하기 위한 다양한 프로그램이 존재합니다.[66][67][68]

주목할 만한 프로그램

라이프 게임에서 만들어진 6366548773467669985195496000번째(6×1027) 세대의 튜링 머신은 해시라이프 모드의 Golly를 사용하여 Intel Core Duo 2 GHz CPU에서 30초 이내에 계산되었습니다.

컴퓨터는 그것이 처음 공개된 이후로 생명의 게임을 따르고 시뮬레이션하는 데 사용되었습니다. 존 콘웨이가 처음으로 다양한 시작 구성이 어떻게 발달했는지 조사할 때, 그는 흑과 백의 돌을 가진 바둑판을 사용하여 손으로 그것들을 추적했습니다. 이것은 지루하고 오류가 발생하기 쉽습니다. 최초의 인터랙티브 게임 오브 라이프 프로그램은 M. J. T. Guy와 S. R. Bourne에 의해 PDP-7용 ALGOL 68C의 초기 버전으로 작성되었습니다. 그 결과는 "그것의 도움이 없었다면, 그 게임에 대한 몇 가지 발견은 어려웠을 것입니다"라는 진술과 함께 Scientific American 1970년 10월호에 발표되었습니다.[1]

게임 오브 라이프의 컬러 버전은 1976년 Ed Hall에 의해 Cromemco 마이크로컴퓨터용으로 작성되었으며, 그 프로그램의 화면이 Byte 1976년 6월호 표지를 채웠습니다.[69] 크로엠코의 마이크로컴퓨터 기반 컬러 그래픽의 등장은 이 게임에 대한 관심을 되살린 것으로 평가되고 있습니다.[70]

가정용 컴퓨터에서 게임 오브 라이프의 두 가지 초기 구현은 BBC BASIC에 쓰여진 말콤 밴소프에 의해 이루어졌습니다. 첫 번째는 Acorn User 잡지 1984년 1월호에 실렸고, 밴소프는 1984년 5월호에 3차원 버전으로 그 뒤를 이었습니다.[71] York 대학의 컴퓨터 과학 교수인 Susan Stephney는 1988년에 1차원 세포 자동차를 생성하는 프로그램인 Life on the Line으로 이것을 추적했습니다.[72]

현재 수천 개의 게임 오브 라이프 프로그램이 온라인에 있으므로 전체 목록은 여기에서 제공되지 않습니다. 다음은 인기나 특이한 기능과 같이 주목할 만한 것에 대한 특별한 주장이 있는 일부 프로그램을 선택한 것입니다. 이러한 프로그램의 대부분은 패턴 편집 및 시뮬레이션을 위한 그래픽 사용자 인터페이스, Game of Life를 포함한 여러 규칙을 시뮬레이션할 수 있는 기능, Game of Life 및 기타 셀룰러 오토마톤 규칙의 흥미로운 패턴 라이브러리를 포함합니다.

  • 골리(Golly)는 Game of Life 및 기타 셀룰러 오토마타(모든 Life-like cellular automata, Mirek's Cellebration의 Generations 계열)를 위한 크로스 플랫폼(Windows, Macintosh, Linux, iOS 및 Android) 오픈 소스 시뮬레이션 시스템입니다. Andrew Trevorrow와 Tomas Rokicki의 John von Neumann의 29-state cellular automaton). 매우 빠른 생성을 위한 해시라이프 알고리즘과 편집 및 시뮬레이션 모두를 위한 Lua 또는 Python 스크립트성이 포함되어 있습니다.
  • Mirek's Cellebration은 Windows용 프리웨어 1차원 및 2차원 셀룰러 오토마타 뷰어, 탐색기 및 편집기입니다. 게임 오브 라이프를 포함한 다양한 셀룰러 오토마톤 규칙을 시뮬레이션하고 볼 수 있는 강력한 시설과 스크립트 가능한 편집기가 포함되어 있습니다.
  • Xlife는 Jon Bennett의 세포 자동화 실험실입니다. 오래 전부터 표준 UNIX X11 Game of Life 시뮬레이션 애플리케이션으로 Windows에도 이식되었습니다. Game of Life와 동일한 인접 환경에서 셀당 최대 8개의 가능한 상태로 셀룰러 자동화 규칙을 처리할 수 있습니다.[73]
  • 블롭 박사의 유기체는 콘웨이의 삶을 기반으로 한 촬영입니다. 게임에서 라이프는 지속적으로 "페트리 접시" 안에 있는 세포 그룹에서 생성됩니다. 형성된 패턴은 더 작은 것들을 내뿜는 성장하는 아메바(실제로는 글라이더)처럼 보이기 위해 매끄럽고 둥글게 되어 있습니다. 특별한 "프로브"는 "블롭"의 핵을 파괴하면서 접시가 넘쳐흐르는 것을 막기 위해 "블롭"을 잽시킵니다.[74]

구글은 2012년 이스터 에그 오브 라이프를 구현했습니다. 용어를 검색한 사용자는 검색 결과 페이지에 게임 구현이 표시됩니다.[75]

비주얼 노벨 어나니머스;코드에는 소설의 줄거리와 연결된 생명의 게임의 기본 구현이 포함되어 있습니다. 어나니머스가 끝날 무렵;게임 내내 여주인공 아이자키 모모에게 문신으로 나타나는 특정 패턴을 게임 오브 라이프에 입력해야 게임이 완성됩니다(콕의 은하, 오픈 소스 게임 오브 라이프 프로그램 골리의 로고와 동일한 패턴).

참고 항목

  • 인공생명 – 연구분야
  • 글로리 시즌 – 1993년 데이비드 브린의 SF 소설은 게임 오브 라이프가 경쟁적인 2인 모드로 진행되는 미래 사회를 배경으로 합니다.
  • Langton's ant – 새로운 행동을 하는 2차원 튜링 기계
  • Poietic Generator – 2차원 매트릭스, "인간" 생명의 게임에서 플레이되는 소셜 네트워크 게임.
  • 자기조직 § 컴퓨터 과학
  • 인간과 만타의 이야기 – Piers Anthony의 공상과학 소설 3부작 소설 'OX'는 게임 오브 라이프를 기반으로 한 세포 자동화 생명체를 특징으로 합니다.
  • 라이프위키 – 콘웨이의 라이프 게임 전용 위키

메모들

  1. ^ 동시성은 각 셀이 주변의 살아있는 이웃의 수를 셀 때 업데이트 후 새 상태가 아닌 업데이트 전에 이웃의 이전 상태를 사용한다는 것을 의미합니다. 만약 세포들이 읽기 순서에 따라 갱신되어 각 세포들이 그 오른쪽과 아래에 있는 세포들의 옛 상태를 사용하지만 그 왼쪽과 위에 있는 세포들의 새로운 상태를 사용한다면, 다른 세포 자동화 결과를 낳습니다. 그것은 콘웨이의 게임 오브 라이프를 프로그래밍하려는 사람들 사이에서 흔한 초보자들의 실수이기 때문에 나이브 라이프로[4][5] 알려져 있습니다.[6]

참고문헌

  1. ^ a b c d Gardner, Martin (October 1970). "The fantastic combinations of John Conway's new solitaire game 'life'" (PDF). Mathematical Games. Scientific American. Vol. 223, no. 4. pp. 120–123. doi:10.1038/scientificamerican1070-120. JSTOR 24927642. Archived (PDF) from the original on 2022-10-09.
  2. ^ a b c d e Berlekamp, E. R.; Conway, John Horton; Guy, R. K. (2001–2004). Winning Ways for your Mathematical Plays (2nd ed.). A K Peters Ltd.
  3. ^ a b c Izhikevich, Eugene M.; Conway, John H.; Seth, Anil (2015-06-21). "Game of Life". Scholarpedia. 10 (6): 1816. Bibcode:2015SchpJ..10.1816I. doi:10.4249/scholarpedia.1816. ISSN 1941-6016.
  4. ^ "NaiveLife Emulated: A reading-order simulation of Life". ConwayLife.com. 24 May 2020. Retrieved 29 November 2021.
  5. ^ Goucher, Adam. "Re: Thread For Your Accidental Discoveries". ConwayLife.com. Retrieved 29 November 2021.
  6. ^ Ian07. "Re: Strange spaceship that is supposed to be impossible and infinite cell spread". ConwayLife.com. Retrieved 29 November 2021. I'm pretty sure this is because you've accidentally created an implementation of what's sometimes known as NaiveLife (as it's a common mistake made by many people coding CGoL for the first time):{{cite web}}: CS1 main: 숫자 이름: 저자 목록 (링크)
  7. ^ Pickover, Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. Sterling Publishing Company, Inc. p. 406. ISBN 978-1402757969.
  8. ^ a b c Schiff, Joel L. (2011). Cellular Automata: A Discrete View of the World. Wiley & Sons, Inc. ISBN 9781118030639.
  9. ^ 존 폰 노이만, "자동화의 일반적이고 논리적인 이론", L.A. Jeffress, Ed., 행동의 뇌 메커니즘 – The Hixon Symposium, John Wiley & Sons, 1951, 1-31쪽.
  10. ^ Kemeny, John G. (1955). "Man viewed as a machine". Sci. Am. 192 (4): 58–67. Bibcode:1955SciAm.192d..58K. doi:10.1038/scientificamerican0455-58.Kemeny, John G. (1955). "Man viewed as a machine". Sci. Am. 192 (4): 58–67. Bibcode:1955SciAm.192d..58K. doi:10.1038/scientificamerican0455-58.과학자 1955; 192:6 (에라타)
  11. ^ Ilachinski, Andrew (2001). Cellular Automata: A Discrete Universe. World Scientific. ISBN 978-981-238-183-5.
  12. ^ Bialynicki-Birula, Iwo; Bialynicka-Birula, Iwona (2004). Modeling Reality: How Computers Mirror Life. Oxford University Press. ISBN 978-0198531005.
  13. ^ von Neumann, John; Burks, Arthur W. (1966). Theory of Self-Reproducing Automata. University of Illinois Press.
  14. ^ 콘웨이, 1999년 4월 14일 '라이프 리스트'에 대한 비공개 통신.
  15. ^ a b 보기에도 재미있고 단순한 것이 복잡한 문제가 될 수 있음을 보여줄 수 있는 모델이자 시뮬레이션입니다.Paul Chapman (11 November 2002). "Life Universal Computer". Retrieved 12 July 2009.
  16. ^ Alstrøm, Preben; Leão, João (1994-04-01). "Self-organized criticality in the game of Life". Physical Review E. 49 (4): R2507–R2508. Bibcode:1994PhRvE..49.2507A. doi:10.1103/PhysRevE.49.R2507. PMID 9961636.
  17. ^ Dennett, D. C. (1991). Consciousness Explained. Boston: Back Bay Books. ISBN 978-0-316-18066-5.
  18. ^ Dennett, D.C. (1995). Darwin's Dangerous Idea: Evolution and the Meanings of Life. New York: Simon & Schuster. ISBN 978-0-684-82471-0.
  19. ^ Dennett, D.C. (2003). Freedom Evolves. New York: Penguin Books. ISBN 978-0-14-200384-8.
  20. ^ Paul Rendell (January 12, 2005). "A Turing Machine in Conway's Game of Life". Retrieved July 12, 2009.
  21. ^ Adam P. Goucher. "Spartan universal computer-constructor". LifeWiki. Retrieved December 5, 2021.
  22. ^ "R-pentomino". LifeWiki. 1983. pp. 219, 223. Retrieved December 5, 2021.
  23. ^ Stephen A. Silver. "Glider". The Life Lexicon. Retrieved March 4, 2019.
  24. ^ "Census Results in Conway's Game of Life". The Online Life-Like CA Soup Search. Archived from the original on 2009-09-10. Retrieved July 12, 2009.
  25. ^ "Spontaneous appeared Spaceships out of Random Dust". Achim Flammenkamp (1995-12-09). Retrieved July 10, 2012.
  26. ^ Stephen A. Silver. "Pulsar". The Life Lexicon. Retrieved March 4, 2019.
  27. ^ Brown, Nico; Cheng, Carson; Jacobi, Tanner; Karpovich, Maia; Merzenich, Matthias; Raucci, David; Riley, Mitchell (5 December 2023). "Conway's Game of Life is Omniperiodic". arXiv:2312.02799 [math.CO].
  28. ^ "LifeWiki:Game of Life Status page - LifeWiki". conwaylife.com. Retrieved 2023-12-16.
  29. ^ Achim Flammenkamp (2004-09-07). "Most seen natural occurring ash objects in Game of Life". Retrieved 2008-09-16.
  30. ^ Stephen A. Silver. "Diehard". The Life Lexicon. Retrieved March 4, 2019.
  31. ^ Koenig, H. (February 21, 2005). "New Methuselah Records". Archived from the original on September 10, 2019. Retrieved January 24, 2009.
  32. ^ Stephen A. Silver. "Gosper glider gun". The Life Lexicon. Retrieved March 4, 2019.
  33. ^ 새로운 허셜 도관의 사냥, 콘웨이라이프 포럼, 2015년 4월 28일, 마이클 심킨("simsim314")과 이동국("Scorbie")의 게시물.
  34. ^ "Block-laying switch engine". LifeWiki. Retrieved December 5, 2021.
  35. ^ Stephen A. Silver. "Infinite Growth". The Life Lexicon. Retrieved March 4, 2019.
  36. ^ Stephen A. Silver. "Rake". The Life Lexicon. Retrieved March 4, 2019.
  37. ^ "Programmable computer". conwaylife.com forums. Retrieved August 23, 2018.
  38. ^ "A Turing Machine in Conway's Game of Life, extendable to a Universal Turing Machine". Paul Rendell. Retrieved August 23, 2018.
  39. ^ "Build a working game of Tetris in Conway's Game of Life". StackExchange. Retrieved August 23, 2018.
  40. ^ "Elementary knightship". Retrieved 9 March 2018.
  41. ^ "초등", 라이프위키, 2018-11-21 회수
  42. ^ Aron, Jacob (16 June 2010). "First replicating creature spawned in life simulator". New Scientist. Retrieved 12 October 2013.
  43. ^ a b "Gemini – LifeWiki". Conwaylife.com. Retrieved 2013-10-16.
  44. ^ "Universal Constructor Based Spaceship". Conwaylife.com. Retrieved 2012-06-24.
  45. ^ "Demonoid". LifeWiki. Retrieved 18 June 2016.
  46. ^ "Geminoid Challenge". Conwaylife.com. Retrieved 2015-06-25.
  47. ^ Passe-Science (2019-05-29). "Automate Cellulaire - Passe-science #27". YouTube. Archived from the original on 2021-12-11. Retrieved 2019-06-25.
  48. ^ apgoucher (2018-11-12). "Fully self-directed replication". Complex Projective 4-Space. Retrieved 2019-06-25.
  49. ^ "0E0P metacell - LifeWiki". www.conwaylife.com. Retrieved 2019-06-24.
  50. ^ Andrzej Okrasinski. "Game of Life Object Statistics". Archived from the original on 2009-07-27. Retrieved July 12, 2009.
  51. ^ Nathaniel Johnston. "The Online Life-Like CA Soup Search". Archived from the original on 2009-09-10. Retrieved July 12, 2009.
  52. ^ Alan Hensel. "About my Conway's Game of Life Applet". Retrieved July 12, 2009.
  53. ^ Nehaniv, Chrystopher L. (15–18 July 2002). Self-Reproduction in Asynchronous Cellular Automata. 2002 NASA/DoD Conference on Evolvable Hardware. Alexandria, Virginia, USA: IEEE Computer Society Press. pp. 201–209. doi:10.1109/EH.2002.1029886. hdl:2299/6834. ISBN 0-7695-1718-8.
  54. ^ "Conway's Game of Life".
  55. ^ 하이라이프 – David Bell의 흥미로운 삶의 변형 (.zip 파일)
  56. ^ Stephen A. Silver. "Replicator". The Life Lexicon. Retrieved March 4, 2019.
  57. ^ "Life-like cellular automata - LifeWiki". Conwaylife.com. Retrieved March 4, 2019.
  58. ^ "Isotropic - LifeWiki". Conwaylife.com. Retrieved March 4, 2019.
  59. ^ "Elementary Cellular Automaton". Wolfram Mathworld. Retrieved July 12, 2009.
  60. ^ "First gliders navigate ever-changing Penrose universe". New Scientist.
  61. ^ 새로운 종류의 과학 온라인, Stephen Wolfram, 클래스 4 시스템의 구조에 대한 참고 (f): 생명의 게임에서의 구조: "한 사람이 무한히 늘어선 검은 세포에서 시작한다면 더 단순한 종류의 무한한 성장이 일어납니다. 그 경우 진화는 사실상 1D이고, 기본 규칙 22를 따르는 것으로 밝혀졌습니다."
  62. ^ "Life Imitates Sierpinski". ConwayLife.com forums. Retrieved July 12, 2009.
  63. ^ Stephen A. Silver. "Immigration". The Life Lexicon. Retrieved March 4, 2019.
  64. ^ Stephen A. Silver. "QuadLife". The Life Lexicon. Retrieved March 4, 2019.
  65. ^ Burraston, Dave; Edmonds, Ernest; Livingstone, Dan; Miranda, Eduardo Reck (2004). "Cellular Automata in MIDI based Computer Music". Proceedings of the 2004 International Computer Music Conference. CiteSeerX 10.1.1.6.3882. hdl:10453/1425. ISBN 9780971319226.
  66. ^ "glitchDS – Cellular Automaton Sequencer For The Nintendo DS". Synthtopia.com. 2008-05-29. Retrieved 2012-06-24.
  67. ^ "Game Of Life Music Sequencer". Synthtopia.com. 2009-04-29. Retrieved 2012-06-24.
  68. ^ "Game Of Life Music Sequencer For iOS, Runxt Life". Synthtopia.com. 2011-01-12. Retrieved 2012-06-24.
  69. ^ Helmers, Carl (June 1976). "About the Cover". Byte. No. 10. pp. 6–7. Retrieved February 18, 2013.
  70. ^ McIntosh, Harold (2008). "Introduction" (PDF). Journal of Cellular Automata. 13: 181–186. Archived (PDF) from the original on 2022-10-09. Retrieved 3 November 2021. With the advent of microcomputers and Cromemco's graphics board, Life became a favorite display program for video monitors and led to a revival of interest in the game.
  71. ^ "Acorn User Magazine Scans". The BBC and Master Computer Public Domain Library. Retrieved 2018-12-29.
  72. ^ Stepney, Susan. "AcornUser articles". www-users.cs.york.ac.uk. AcornUser. Retrieved 2018-12-29.
  73. ^ "Xlife".
  74. ^ "Dr. Blob's Organism freeware".
  75. ^ Wasserman, Todd (12 July 2012). "Type 'Conway's Game of Life' on Google and See What Happens". Mashable. Retrieved 1 May 2020.

외부 링크

Wikimedia Commons에는 Game of Life와 관련된 미디어가 있습니다.