튜링 후기
Post–Turing machine이 기사에는 여러 가지 문제가 있습니다. 개선을 도와주시거나 토크 페이지에서 이러한 문제에 대해 논의해 주시기 바랍니다. (이러한 템플릿 메시지를 제거하는 방법 및 시기에 대해 알아보기) |
| 튜링머신 |
|---|
| 기계. |
| 변종 |
| 과학 |
튜링 후 기계는 에밀 포스트의 튜링 등가 계산[1] 모델의 변형으로 구성된 튜링 기계 유형의 "프로그램 공식"입니다. 포스트의 모델과 튜링의 모델은 서로 매우 비슷하지만 독립적으로 개발되었습니다. 튜링의 논문은 1936년 5월에 출판을 위해 접수되었고, 포스트의 논문은 10월에 출판되었습니다. Post-Turing 기계는 바이너리 알파벳, 무한히 많은 바이너리 저장 위치들, 그리고 저장 위치들 간의 양방향 이동과 그들의 내용들의 변경을 위한 명령들을 가진 원시적인 프로그래밍 언어를 사용합니다. "Post-Turing program"과 "Post-Turing machine"이라는 이름은 1973-1974년에 Martin Davis에 의해 사용되었습니다(Davis 1973, p. 69ff). 이후 1980년에 데이비스는 "Turing–Post program"이라는 이름을 사용했습니다(Davis, Steen p. 241).
1936년: 포스트 모델
1936년 그의 논문 "Finite Combinatory Processes"에서—공식 1", 에밀 포스트는 "논리적으로 재발성과 동등하다"고 추측하는 모델을 설명했습니다.
포스트의 계산 모델은 튜링 기계 모델과 달리 인간 "컴퓨터"가 계산 중에 수행할 행위에 대한 추가적인 "원자화"에서 차이가 있습니다.[2]
포스트의 모델은 "공간 또는 상자의 쌍방향 무한 시퀀스"로 구성된 "심벌 공간"을 사용하며, 각 상자는 "표시"(단일 수직 스트로크로 표시됨)와 "표시되지 않음"(공백)의 두 가지 가능한 조건 중 하나에 있을 수 있습니다. 처음에는 많은 상자가 표시되어 있고 나머지 상자는 표시되어 있지 않습니다. 그런 다음 "작업자"는 순서대로 번호가 매겨진 고정된 유한 "방향 집합"(명령어)에 따라 한 번에 하나의 상자 안에서 작동하면서 상자 사이를 이동합니다. 작업자는 "시작점으로 지정된" 상자에서 시작하여 지침 1부터 시작하여 한 번에 하나씩 지침 집합을 따릅니다.
작업자가 수행할 수 있는 기본 작업은 5가지입니다.
- (a) 상자가 비어 있는 경우 상자에 표시
- (b) 상자에 표시된 경우 해당 상자의 표시를 지웁니다.
- (c) 오른쪽 상자로 이동
- (d) 왼쪽 상자로 이동
- (e) 상자가 들어 있는지, 표시되어 있지 않은지 확인합니다.
그러면 작업자에게 주어진 i "방향"(지시)은 다음과 같은 형태 중 하나가 됩니다.
- O [O = (a), (b), (c) 또는 (d)] 작업을 수행한 후 j 방향을 따릅니다.
- (e) 작업을 수행하고 대답이 예 또는 아니오이므로 대응하여i j' 또는i j' 방향을 따릅니다.
- 그만.
(위의 들여쓰기 텍스트 및 이탤릭체는 원본과 같습니다.) 이 공식이 "초기 단계의 개발"이라는 포스트 발언은 다음을 포함하여 최종 "확정적인 형태"에서 "더 큰 유연성"에 대한 몇 가지 가능성을 언급합니다.
- 상자의 무한대를 유한한 확장 가능한 기호 공간으로 대체하는 "프로세스가 진행됨에 따라 주어진 유한 기호 공간의 필요한 확장을 허용하기 위한 원시 연산 extending",
- 두 개 이상의 기호로 이루어진 알파벳을 사용하여 "상자를 표시하는 하나 이상의 방법",
- "작업자가 식별하고 상자에서 상자로 이동할 수 있는 포인터 역할을 하는 물리적 개체"를 소개합니다.
1947: 포스트가 공식적으로 튜링 5-튜플을 4-튜플로 축소했습니다.
튜링 기계라는 기사에서 간단히 언급되었듯이, 포스트는 1947년 그의 논문에서 튜링 5쌍을 4쌍으로 원자화시켰습니다.
- "우리의 네 쌍둥이는 튜링 개발에서 다섯 쌍둥이입니다. 즉, 우리의 표준 지침이 인쇄(오버프린팅) 또는 모션(왼쪽 또는 오른쪽)을 명령하는 경우 튜링의 표준 지침은 항상 인쇄 및 모션(오른쪽, 왼쪽 또는 없음)을 명령합니다.(각주 12, Uncedible, p. 300)
튜링과 마찬가지로 그는 삭제를 기호 "S0"을 인쇄하는 것으로 정의했습니다. 그래서 그의 모델은 세 가지 유형(cf)의 쿼드러플만 인정했습니다. 미확정, 페이지 294):
- qSLqijl,
- qSRqijl,
- qi Sj Sk ql
당시 그는 여전히 튜링 국가-기계 협약을 유지하고 있었습니다. 그는 기호의 특정 테스트가 다른 곳에서 실행을 "브랜치"할 때까지 단계의 가정된 순차 실행의 개념을 공식화하지 않았습니다.
1954년, 1957년: 왕 모델
여기에 제시된 Wang 모델을 4가지 지침으로 더 축소하려면 Wang B-machine을 참조하십시오.
왕(1957, 그러나 1954년 ACM에 제출)은 종종 인용됩니다(cf). 민스키(Minsky, 1967, p. 200)는 이진 테이프 튜링 기계의 "프로그램 공식"의 원천으로서 집합의 번호가 매겨진 명령어를 사용합니다.
- 0을 쓰다
- 1을 쓰다
- 왼쪽으로 옮기다
- 오른쪽으로 움직입니다
- 0을 스캔하면 명령 i로 이동합니다.
- 1을 스캔하면 명령 j로 이동합니다.
이진 테이프 튜링 기계는 위의 지침을 사용하여 동등한 "왕 프로그램"으로 쉽게 변환됩니다.
1974년: 최초의 데이비스 모델
마틴 데이비스는 에밀 포스트의 학부생이었습니다. Stephen Kleene과 함께 Alonzo Church 아래에서 박사학위를 마쳤습니다(Davis (2000) 1, 2번째 각주 p. 188).
그는 1973-1974년에 뉴욕 대학교의 쿠랑 연구소에서 일련의 강의에서 다음과 같은 모델을 제시했습니다. 이것은 데이비스가 공식적으로 "Post-Turing 언어"와 함께 "Post-Turing machine"이라는 이름을 적용한 모델입니다.[2] 지침은 순차적으로 실행되는 것으로 가정합니다(Davis 1974, 페이지 71).
1978년: 두 번째 데이비스 모델
다음 모델은 에세이로 나타납니다. 계산이란 무엇인가요? 스티븐 241-267쪽에서. 어떤 이유에서인지 Davis는 자신의 모델 이름을 "Turing-Post machine"(256페이지에 백슬라이딩 하나 포함)으로 변경했습니다.
다음 모델에서 Davis는 숫자 "1"을 Post의 "mark/slash"에 할당하고 "0"을 빈 칸에 할당합니다. 데이비스의 말을 인용하자면, "우리는 이제 튜링-포스트 프로그래밍 언어를 도입할 준비가 되었습니다. 이 언어에는 7가지 종류의 지시사항이 있습니다.
- "프린트 1
- "인쇄 0
- "오른쪽으로 이동"
- "왼쪽으로 이동"
- "1이 스캔되면 i단계로 이동합니다.
- "0이 스캔되면 i단계로 이동합니다.
- "STOP"
"그러면 튜링 포스트 프로그램은 각각 이 7가지 종류 중 하나인 명령어의 목록입니다. 물론 실제 프로그램에서는 다섯 번째 또는 여섯 번째 단계의 문자 i를 정(+)의 정수로 대체해야 합니다."(Davis in Steen, 247쪽).
1994년 (제2판): 데이비스-시갈-Weyuker의 Post-Turing 프로그램 모델
"비록 우리가 제시한 튜링의 공식은 원래 에밀 포스트가 제시한 것과 정신적으로 더 가깝지만, 이 공식을 그렇게 적절하게 보이게 만든 것은 튜링의 계산 분석이었습니다. 이 언어는 이론 컴퓨터 과학에서 근본적인 역할을 했습니다." (Davis et al. (1994) p. 129)
이 모델은 여러 기호를 인쇄할 수 있습니다. 이 모델은0 S 대신 B(공백)를 사용할 수 있습니다. 테이프는 양방향으로 무한합니다. 헤드 또는 테이프가 움직이지만 RIGHT와 LEFT의 정의는 항상 두 경우 모두 동일한 결과를 나타냅니다(Turing은 동일한 규칙을 사용했습니다).
- PRINT σ;스캔된 기호를 with로 바꿉니다.
- 스캔한 기호가 σ이면 σ '첫 번째' 명령어 'L'로 이동합니다.
- RIGHT ;현재 스캔된 사각형의 바로 오른쪽 스캔
- LEFT;현재 스캔된 사각형의 바로 왼쪽 스캔
이 모델은 다음과 같이 위에 제시된 이진 {0, 1} 버전으로 축소됩니다.
- 인쇄 0 = ERASE;스캔된 기호를 0 = B = 블랭크로 바꿉니다.
- 인쇄 1;스캔된 기호를 1로 바꿉니다.
- 스캔된 기호가 0인 경우 "첫 번째" 지침 레이블 L로 이동합니다.
- 스캔된 기호가 1인 경우 "첫 번째" 지침 레이블 L로 이동합니다.
- RIGHT ;현재 스캔된 사각형의 바로 오른쪽 스캔
- LEFT;현재 스캔된 사각형의 바로 왼쪽 스캔
Post-Turing 기계의 예
튜링의 원자화는 튜링 후 명령의 연속으로 5중으로 이루어집니다.
2기호 튜링 5쌍에서 2기호 Post-Turing 명령어 시퀀스에 이르기까지 다음과 같은 "축소"(분해, 미립화) 방법은 민스키(1961)에서 찾을 수 있습니다. 그는 이러한 "프로그램... 일련의 지시"로의 축소가 Hao Wang의 B-machine(본래의 이탈리아어, cf)의 정신에 있다고 말합니다. Minsky (1961) p. 439).
(민스키는 "서브 루틴"이라고 부르는 것으로 축소하면 7개의 Post-Turing 명령어가 아닌 5개의 명령어가 생성됩니다. 그는 Wi0: "기호 Si0; 새로운 상태 Mi0", Wi1: "기호 Si1; 새로운 상태 Mi1"을 미립화하지 않았습니다. 다음 방법은 Wi0 및 Wi1을 더욱 미립화합니다. 다른 모든 점에서는 방법이 동일합니다.)
이렇게 튜링 5-튜링을 Post-Turing 명령으로 축소하는 것은 "효율적인" Post-Turing 프로그램으로 귀결되지 않을 수 있지만, 원래의 튜링 프로그램에 충실할 것입니다.
다음 예제에서 2-상태 비지 비버의 각 튜링 5-쌍은 다음과 같이 변환합니다.
- 첫 번째 조건 "jump"(go, branch), 다음에 오는
- "0" 케이스에 대한 테이프 작업 지침서 2개 – 인쇄 또는 지우기 또는 없음, 왼쪽 또는 오른쪽 또는 없음, 다음 순서입니다.
- "0"인 경우의 다음 명령에 대한 무조건적인 "jump"
- "1" 케이스에 대한 테이프 작업 지침 2개 – 인쇄 또는 지우기 또는 없음, 왼쪽 또는 오른쪽 또는 없음, 다음 순서입니다.
- "1"의 경우에 대한 다음 지시에 대한 무조건적인 "jump".
Turing-state 당 총 1 + 2 + 1 + 2 + 1 = 7개의 명령어에 대해.
예를 들어, 5-튜플의 두 줄로 쓰여진 2-상태 바쁜 비버의 "A" 튜링-상태는 다음과 같습니다.
| 초기 m-구성(Turing state) | 테이프 기호 | 인쇄작업 | 테이프 모션 | 최종 m-구성(Turing state) |
|---|---|---|---|---|
| A | 0 | P | R | B |
| A | 1 | P | L | B |
표는 단일 튜링 "명령어"를 나타내지만, 우리는 표가 "머리 밑 tup 기호 = 1"인 경우와 "머리 밑 tape 기호 = 0"인 경우의 5-tape 두 줄로 구성되어 있음을 알 수 있습니다. 튜링은 왼쪽 두 열인 "m-구성"과 "기호"는 기계의 현재 "구성"(그 순간의 테이프와 테이블을 모두 포함한 상태)을 나타내고 마지막 세 열은 그 이후의 "동작"임을 관찰했습니다(결정할 수 없음, 페이지 119). 기계가 동시에 두 개의 "상태"에 있을 수 없기 때문에, 기계는 한 구성 또는 다른 구성 중 하나에 "분지"해야 합니다.
| 초기 m-구성 및 기호 S | 인쇄작업 | 테이프 모션 | 최종 m-구성 |
|---|---|---|---|
| S=0 → | P → | R → | B |
| → A < | |||
| S=1 → | P → | L → | B |
"구성 분기"(J1 xx) 또는 "J0 xx"(J0 xx) 후에 시스템은 두 개의 후속 "동작" 중 하나를 따릅니다. 이 두 가지 동작을 한 줄에 나열하고 순차적으로 번호(또는 레이블)를 지정합니다. 각 점프(지점, 이동) 아래에 "숫자"(주소, 위치)로 점프를 배치합니다.
| 초기 m-구성 & 기호 S | 인쇄작업 | 테이프 모션 | 최종 m-구성 케이스 S=0 | 인쇄작업 | 테이프 모션 | 최종 m-구성 케이스 S=1 | |
|---|---|---|---|---|---|---|---|
| S=0인 경우: | P | R | B | ||||
| → A < | |||||||
| S=1인 경우: | P | L | B | ||||
| 지시 # | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 튜링후지시 | 제이원 | P | R | J | P | L | J |
| 바로 설명하기 # | 5 | B | B |
Post-Turing machine 규칙에 따라 Print, Erase, Left, and Right 명령은 다음 두 가지 작업으로 구성됩니다.
- 테이프 작업: {P, E, L, R}, 그러면
- 테이블 작업: 다음 지침으로 순서대로 이동
그리고 Post-Turing 머신 규약에 따라 조건부 "점프" J0xx, J1xx는 두 가지 동작으로 구성됩니다.
- 테이프 작업: 머리 아래 테이프에 있는 기호 보기
- 테이블 작업: 기호가 0(1)이고 J0(J1)이면 xxx로 이동합니다. 그렇지 않으면 다음 순서로 이동합니다.
그리고 Post-Turing 머신 규칙에 따르면 무조건적인 "점프" Jxx는 단일 액션으로 구성됩니다. 또는 2-액션 시퀀스를 정규화하려면 다음과 같습니다.
- 테이프 작업: 머리 아래 테이프에 있는 기호 보기
- 테이블 작업: 기호가 0이면 xxx로 이동하고 기호가 1이면 xxx로 이동합니다.
어떤 것과 몇 개의 점프가 필요합니까? 무조건 점프 Jxx는 단순히 J0이고 바로 뒤에 J1(또는 그 반대)이 뒤따릅니다. Wang(1957)은 또한 J0xx 또는 J1xx 중 하나의 조건부 점프만 필요하다는 것을 보여줍니다. 그러나 이 제한으로 기계는 설명서를 작성하기가 어려워집니다. 종종 두 개만 사용됩니다.
- { J0xxx, J1xxx }
- { J1xxx, Jxxx }
- { J0xxx, Jxxx },
그러나 J0xx, J1xx, Jxxx} 세 가지를 모두 사용하면 추가 명령이 제거됩니다. 2-상태 Busy Bever 예제에서는 {J1xx, Jxxx}만 사용합니다.
2주간 바쁜 비버
바쁜 비버의 임무는 멈추기 전에 가능한 한 많은 것을 인쇄하는 것입니다. "Print" 명령은 1, "Erase" 명령은 0(즉, P0과 동일)을 씁니다. 테이프가 "왼쪽" 또는 "오른쪽"으로 이동합니다(즉, "머리"가 고정되어 있음).
2-상태 튜링 기계 바쁜 비버의 상태표:
| 테이프 기호 | 현재상태A | 현재상태B | ||||
|---|---|---|---|---|---|---|
| 쓰기 기호 | 테이프이동 | 넥스트 스테이트 | 쓰기 기호 | 테이프이동 | 넥스트 스테이트 | |
| 0 | 1 | R | B | 1 | L | A |
| 1 | 1 | L | B | 1 | N | H |
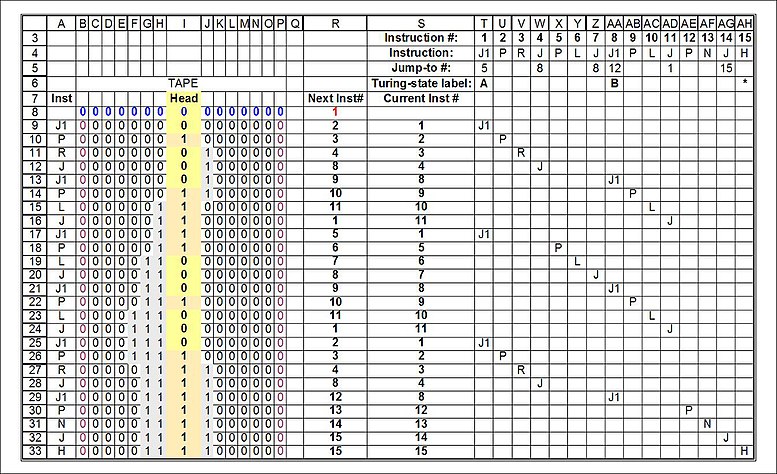
2-상태 바쁜 비버의 Post-Turing 버전에 대한 지침: 모든 지침이 동일한 라인에 있고 순서대로 있는지 관찰합니다. 이것은 "튜링" 버전에서 크게 벗어난 것이며 "컴퓨터 프로그램"이라고 불리는 것과 같은 형식입니다.
| 지침 # | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 설명 | 제이원 | P | R | J | P | L | J | 제이원 | P | L | J | P | N | J | H |
| #로 점프하기 | 5 | 8 | 8 | 12 | 1 | 15 | |||||||||
| 튜링 국가 레이블 | A | B | H |
또는 테이블을 문자열로 쓸 수도 있습니다. "매개변수 구분자" ":"와 명령 구분자 ""를 사용하는 것은 전적으로 우리가 선택한 것이며 모형에 나타나지 않습니다. 상태도 규칙을 지침과 결합하는 방법(즉, 점프의 목적지를 표시하기 위해 화살표를 사용하는 방법)에 대한 유용한 아이디어는 규칙이 없습니다(그러나 부스(1967) p. 374, 불로스와 제프리(1974, 1999) p. 23 참조). 바로 아래 예에서 명령어는 "1"부터 순차적으로 시작되며, 매개 변수/"operand"는 명령어/"opcode"의 일부로 간주됩니다.
- J1:5, P, R, J:8, P, L, J:8, J1:12, P, L, J1:1, P, N, J:15, H
메모들
- ^ Rajendra Kumar, 오토마타 이론, Tata McGraw-Hill Education, 2010, p. 343
- ^ a b 그의 XIII Computable Functions에서 Kleene은 Post 모델을 채택하고 있습니다. Kleene의 모델은 공백과 하나의 기호 "tall mark ¤"를 사용합니다(Kleene p. 358). 이는 Post 1936에 더 가까운 치료법입니다. Post 1936은 2방향 무한 테이프와 단 하나의 기호를 사용한 계산을 고려했습니다."(클린 페이지 361). Kleene은 Post의 치료가 "튜링법"(Kleene p. 379)의 "원자적 행위"(Kleene p. 357)에 대한 추가 감소를 제공했다고 관찰합니다. Kleene에 의해 설명된 바와 같이, "튜링 액트"는 튜링 테이블의 행에 지정된 3개의 (시순차적) 동작을 조합한 것입니다: (i) 인쇄-기호/소거/해제/해제 뒤에 (ii) 이동-테이프-좌측/이동-테이프-우측/해제 뒤에 (iii) 테스트-테이프-고-다음 명령어: 예: "s1Rq1"은 "인쇄 기호 "¤"를 의미하고 테이프를 오른쪽으로 이동합니다. 테이프 기호가 "¤"이면 상태 q1"로 이동합니다. (클린의 예 페이지 358 참조) Kleene은 Post가 이러한 3개의 동작을 두 가지 유형의 2개 동작으로 더 미립화했음을 관찰합니다. 첫 번째 유형은 "인쇄/지우기" 작업이고, 두 번째 유형은 "테이프 왼쪽/오른쪽 이동 작업"입니다: (1.i) 인쇄-기호/지우기/삭제/실행-다음 명령어, (1.ii) 테이프 왼쪽/이동-테이프 오른쪽/실행-실행-다음 명령어. (2.ii) 테이프 왼쪽/삭제/실행-실행-다음 명령어. 하지만 Kleene은 그것을 보지만,
- "실제로 튜링 기계법은 이미 복합적이고, 심리적으로 인쇄와 정신 상태의 변화로 구성되어 있으며, 동작과 또 다른 정신 상태가 뒤따른다고 주장할 수 있습니다. [그리고] 포스트 1947은 튜링 기계법을 두 개로 분리합니다. 우리는 여기에 있지 않습니다. 주로 기계 테이블의 공간을 절약하여 그렇게 하지 않기 때문입니다."(Kleene p. 379)
참고문헌
- 스티븐 C. Kleene, 메타수학 입문, North-Holland 출판사, 뉴욕, 1991년 10판, 1952년 초판. 13장은 튜링 기계에 대한 훌륭한 설명입니다. Kleene은 그의 설명에서 Post-like 모델을 사용하고 튜링 모델이 더 원자화될 수 있다는 것을 인정합니다. 각주 1을 참조하십시오.
- 마틴 데이비스 편집장: 결정 불가능한 명제, 해결 불가능한 문제와 계산 가능 함수에 관한 결정 불가능한 기초 논문, 레이븐 프레스, 뉴욕, 1965. 논문으로는 괴델, 교회, 로저, 크린, 포스트 등이 있습니다.
- 마틴 데이비스, "계산이란 무엇인가", 수학투데이, 린 아서스틴, 빈티지 북스(랜덤하우스), 1980. 튜링 머신에 대해 쓴 것 중 최고의 논문일 수도 있습니다. Davis는 Post의 계산 모델을 기반으로 튜링 머신을 훨씬 단순한 모델로 축소합니다. 에밀 포스트의 작은 전기를 포함합니다.
- 마틴 데이비스, 계산 가능성: 배리 제이콥스의 노트, 뉴욕 대학교 쿠란트 수학 과학 연구소, 1974.
- 마틴 데이비스, 론 시걸, 일레인 J. Weyuker, (1994) 계산 가능성, 복잡성 및 언어: 이론 컴퓨터 과학의 기초 – 제2판, 학술 출판부: Harcourt, Brace & Company, San Diego, 1994 ISBN0-12-206382-1 (초판, 1983)
- 프레드 헤니, 계산 가능성 소개, 애디슨–웨슬리, 1977.
- 마빈 민스키(Marvin Minsky, 1961), 포스트의 '태그' 문제의 재귀적 해결 불가능과 튜링 기계 이론의 다른 주제들, 수학 연보, 제74권, 제3호, 1961년 11월.
- 로저 펜로즈, 황제의 새로운 마음: 컴퓨터, 마음 그리고 물리학 법칙에 관하여, 옥스포드 대학교 출판부, 옥스포드 영국, 1990 (수정 포함). cf. 2장 "알고리즘과 튜링 머신" 지나치게 복잡한 프레젠테이션(더 나은 모델은 데이비스의 논문 참조)이지만 튜링 기계와 정지 문제, 그리고 처치의 람다 미적분학에 대한 철저한 프레젠테이션.
- Hao Wang (1957): "튜링의 컴퓨터 기계 이론의 변형", 컴퓨터 기계 협회 (JACM) 저널 4, 63–92.