물리학의 시간

시간을
주요 개념 과거. 현재의. 미래. 영원 세상의
연구 분야 고고학 연표 역사 호롤로지 고생물학 미래학
철학 프리젠티즘 영원론 이벤트 운명론
종교 신화 창조. 종료 시간 심판의 날 불멸 애프터라이프 환생 칼라차크라
측정. 표준 ISO 8601 미터법 16진수
과학 자연주의 시간생물학 우주론 진화 방사성 연대 측정 우주의 궁극적 운명 물리학의 시간
관련 토픽 운동 공간 시공간 시간 여행
v t

물리학에서 시간은 그 측정에 의해 정의된다: 시간은 시계를 ^[1]읽는 것이다.고전적이고 상대적이지 않은 물리학에서는 스칼라량(흔히 $기호{\displaystyle }$ t$\displaystyle$t로 표시됨)이며, 길이, 질량 및 전하와 마찬가지로 일반적으로 기본량으로 기술됩니다.시간은 다른 물리량과 수학적으로 결합되어 운동, 운동 에너지, 시간 의존 장과 같은 다른 개념을 도출할 수 있다.타임키핑은 기술적, 과학적 문제의 복합체이며 기록의 기초 중 일부입니다.

시간의 표시

시계가 존재하기 전에는 시간은 각 문명의 ^[3]시대가 이해할 수 있는 물리적^[2] 과정으로 측정되었습니다.

• 매년^[3] 나일강의 홍수를 나타내는 시리우스의 첫 등장(헬리아칼 상승 참조)
• 외견상^[4] 영원히 밤과 낮의 주기적인 연속
• 새벽녘에^[5] 태양이 처음 나타날 때의 지평선상의 위치
• 하늘의^[6] 태양의 위치
• 낮의^[7] 낮 시간 표시
• 노몬이^[8] 드리우는 그림자의 길이

결국,^[9][10] 작동 정의를 사용하여 계측으로 시간의 경과를 특징짓는 것이 가능해졌다.동시에,^[11] 이하와 같이, 시간에 대한 개념이 진화했습니다.

시간 측정 단위: 두 번째

SI(International System of Units)에서 시간 단위는 두 번째(기호: $\$입니다$.$이는 SI 염기 단위이며 1967년부터 "세슘 133 ^[12]원자의 지면 상태의 두 초미세 수준 간 전이에 해당하는 방사선의 지속 시간"으로 정의되었다.이 정의는 세슘 원자 시계의 작동에 기초하고 있습니다.이 시계들은 1955년 이후 1차 기준 표준으로 실용화되었고 그 이후로 계속 사용되고 있다.

타임 키핑의 최첨단

전제 조건
측정. 과학적 표기법 자연 단위

전 세계에서 사용되고 있는 UTC 타임스탬프는 원자 시간 표준입니다.이러한 시간 표준의 상대적 정확도는 현재 10^−15[13](약 3000만 년 중 1초에 해당) 수준이다.이론적으로 관측 가능한 것으로 간주되는 가장 작은 시간 단계는 플랑크 시간이라고 불리며, 이는 약⁻⁴⁴ 5.391×10초입니다. 이는 현재 시간 표준의 분해능보다 훨씬 낮은 크기입니다.

세슘 원자 시계는 1950년 이후 실용화되었고, 전자제품의 발달로 마이크로파 주파수를 안정적으로 측정할 수 있게 되었다.한층 더 진보함에 따라, 원자 시계 연구는 그 어느 때보다 높은 주파수로 진행되어 더 높은 정확도와 더 높은 정밀도를 제공할 수 있다.이러한 기술에 기초한 클럭은 개발되었지만 아직 기본 참조 표준으로 사용되지 않습니다.

시간의 개념

갈릴레오, 뉴턴, 그리고 20세기까지 대부분의 사람들은 시간은 모든 곳에서 같은 것이라고 생각했다.이는 타임라인의 기초이며 time은 파라미터입니다.시간에 대한 현대적 이해는 상대적인 운동에 따라 시간의 속도가 달라지고 시공간이 합쳐지는 아인슈타인의 상대성이론에 기초하고 있다.이 뷰에서 시간은 좌표입니다.빅뱅 이론의 지배적인 우주론적 모델에 따르면, 시간 자체는 약 138억 년 전 우주의 일부로 시작되었다.

자연의 규칙성

시간을 측정하기 위해 어떤 주기적인 현상의 발생(이벤트) 횟수를 기록할 수 있다.계절의 규칙적인 반복, 태양, 달, 별의 움직임은 물리 법칙이 공식화되기 전에 수천 년 동안 기록되고 표로 작성되었습니다.태양은 시간의 흐름을 결정하는 존재였지만, 시간은 수천 년 동안 시간에만 알려져 있었기 때문에, 그노몬의 사용은 세계 대부분, 특히 유라시아, 그리고 적어도 동남아시아의 ^[15]정글만큼 남쪽으로 알려져 있었다.

특히, 종교적인 목적으로 유지된 천문대는 별들, 심지어 일부 행성들의 규칙적인 움직임을 확인할 수 있을 만큼 정확해졌다.

처음에는 성직자들이 수작업으로 시간을 기록했고, 다음에는 상거래를 위해 파수꾼들이 그들의 임무의 일부로 시간을 기록했습니다.분점, 모래시계, 물시계의 표가 점점 더 정확해지고 마침내 믿을 수 있게 되었다.바다에 있는 배의 경우, 소년들은 모래잔을 돌리고 시간을 알리는 데 사용되었다.

기계 시계

월링포드의 리처드(1292–1336), 세인트루이스의 수도원장.알반 ^[16][17]수도원은 1330년경에 천문학적 오레리로 기계 시계를 만든 것으로 유명하다.

월링포드의 리차드 시대에, 래칫과 기어의 사용은 유럽의 도시들이 각각의 도시 시계에 시간을 표시하는 메커니즘을 만들 수 있게 해주었다; 과학 혁명의 시기에는, 시계가 가족들이 개인 시계나 아마도 회중시계를 공유할 수 있을 만큼 충분히 작아졌다.처음에는 왕들만 그것들을 살 수 있었다.진자 시계는 18세기와 19세기에 널리 사용되었다.그것들은 일반적으로 석영과 디지털 시계에 의해 대체되었다.원자 시계는 이론적으로 수백만 년 동안 정확한 시간을 유지할 수 있다.표준 및 과학적 용도에 적합합니다.

갈릴레오: 시간의 흐름

1583년, 갈릴레오 갈릴레이 (1564–1642)는 진자의 조화 운동이 일정한 주기를 가지고 있다는 것을 발견했고, 그는 피사 대성당의 질량의 조화 운동에서 흔들리는 램프의 움직임을 그의 ^[18]맥박으로 시간을 쟀다.

그의 Two New Sciences (1638)에서, 갈릴레오는 물시계를 사용하여 청동 공이 알려진 거리를 경사면으로 굴리는 데 걸리는 시간을 측정하였습니다; 이 시계는 다음과 같습니다.

"높은 위치에 놓인 큰 물 그릇; 이 그릇의 바닥에는 작은 직경의 파이프가 납땜되어 있고, 우리는 수로의 전체 길이 또는 길이의 일부 동안 각각의 강하 동안 작은 유리로 수집했습니다; 이렇게 수집된 물은 각 강하 후에 무게를 쟀습니다.매우 정확한 균형으로 보면, 이러한 무게의 차이와 비율은 시간의 차이와 비율을 제공했고, 이는 연산이 여러 번 반복되었지만 결과에 ^[19]현저한 차이는 없었습니다."

공의 움직임을 설명하기 위해 문자 그대로의 시간의 흐름을 측정하는 갈릴레오의 실험 설정은 아이작 뉴턴의 프린키피아에서 다음과 같이 진술하기 전에 이루어졌다.

나는 시간, 공간, 장소, 움직임을 모두에게 잘 알려진 것으로 정의하지 않는다.^[20]

갈릴레오 변환에서는 모든 기준 프레임에 대해 시간이 동일하다고 가정합니다.

뉴턴의 물리학: 선형 시간

1665년 또는 그 무렵, 아이작 뉴턴(1643–1727)이 중력에 의해 떨어지는 물체의 운동을 유도했을 때, 시간 처리에 대한 수학 물리학의 첫 번째 명확한 공식은 시작되었는데, 그것은 바로 만능 시계로 생각되는 선형 시간이었다.

절대, 진실, 수학적 시간은 그 자체의 성질에서 외부와 관계 없이 균등하게 흐른다.다른 이름으로 지속시간이라고 불린다.상대, 명백한, 공통시간은 운동수단에 의한 지속시간의 합리적이고 외부적인 측정치이며, 일반적으로 ti 대신 사용된다.1시간, 1일, 1개월, 1년 등입니다.^[21]

갈릴레오가 설명한 물시계 메커니즘은 실험 중에 물의 층류를 제공하도록 설계되었으며, 따라서 실험 기간 동안 지속적인 물의 흐름을 제공하고, 뉴턴이 지속 시간이라고 부르는 것을 구체화했다.

이 절에서 아래에 열거된 관계는 시간을 고려 중인 물리적 시스템의 동작에 대한 지표가 되는 매개 변수로 취급합니다.뉴턴의 유향은 선형적인 시간의 흐름을 다루기 때문에, 시간은 선형적으로 변화하는 매개 변수, 즉 시계 면에 있는 시간의 행진을 추상화한 것으로 여겨질 수 있습니다.달력과 배의 일지를 시간, 일, 월, 년, 세기의 행진에 매핑할 수 있다.

전제 조건
미분 방정식 편미분 방정식

열역학과 불가역성의 역설

1798년까지, 벤자민 톰슨 (1753–1814)은 일이 무제한으로 열로 바뀔 수 있다는 것을 발견했습니다 - 에너지 보존의 선구자 또는

• 열역학 제1법칙

1824년, Sadi Carnot (1796–1832)는 추상 엔진인 Carnot 사이클로 증기 엔진을 과학적으로 분석했습니다.Rudolf Clausius(1822–1888)는 무질서, 즉 엔트로피의 측정에 주목했으며, 이는 카르노 엔진에서 사용할 수 있는 자유 에너지의 지속적인 감소에 영향을 미칩니다.

• 열역학 제2법칙

따라서 열역학적 시스템의 지속적인 행진은, 주어진 온도에서, 더 작은 엔트로피에서 더 큰 엔트로피로, 시간의 화살을 정의합니다.특히 스티븐 호킹은 ^[22]세 가지 시간의 화살을 식별한다.

• 심리적인 시간의 화살 - 멈출 수 없는 흐름에 대한 우리의 인식.
• 시간의 열역학 화살 - 엔트로피의 증가로 구분됩니다.
• 우주론적 시간의 화살 - 우주의 팽창으로 특징지어진다.

시간이 지남에 따라 고립된 열역학 시스템에서 엔트로피가 증가합니다.이와는 대조적으로, 에르빈 슈뢰딩거 (1887–1961)는 인생은 "부정적인 엔트로피 흐름"^[23]에 의존한다고 지적했다.일리야 프리고긴(1917–2003)은 생명체와 마찬가지로 평형에서 멀리 떨어져 있는 다른 열역학 시스템도 생명을 연상시키는 안정된 시공간 구조를 보일 수 있다고 말했다.곧이어, 화학 ^[25]용액에서 진동하는 색을 보여주는 벨루소프-자보틴스키 반응이^[24] 보고되었다.이러한 평형하지 않은 열역학적 가지는 불안정한 분기점에 도달하고,^[26] 다른 열역학적 가지는 그 대신 안정됩니다.

전자기 및 빛의 속도

1864년, 제임스 클러크 맥스웰 (1831–1879)은 전기와 자기 결합 이론을 발표했다.그는 그 두 현상에 관해 알려진 모든 법칙을 4개의 방정식으로 결합했다.이러한 방정식은 맥스웰의 전자기 방정식으로 알려져 있습니다. 전자파 형태의 해답을 허용하고 전자파를 발생시킨 전하의 속도에 관계없이 일정한 속도 c로 전파됩니다.

빛이 항상 속도 c로 이동할 것으로 예측된다는 사실은 만약 맥스웰의 방정식이 관성 프레임(등속도의 기준 프레임)에 유지된다고 가정한다면 갈릴레이의 상대성 이론과 양립할 수 없을 것이다. 왜냐하면 갈릴레이 변환은 평행하게 이동하는 관찰자의 기준 프레임에서 속도가 감소(또는 증가)할 것을 예측하기 때문이다.빛에 대한 역평행(또는 역평행)을 나타냅니다.

맥스웰의 방정식이 알려진 형태로 수정되지 않은 광택 에테르라는 절대 기준 프레임이 하나 있을 것으로 예상되었다.

Michelson-Morley 실험은 발광 에테르에 대한 지구의 움직임으로 인해 빛의 상대 속도 차이를 발견하지 못했는데, 이는 맥스웰의 방정식이 사실상 모든 프레임에서 유효하다는 것을 암시한다.1875년, 헨드릭 로렌츠(1853–1928)는 맥스웰의 방정식을 변경하지 않은 로렌츠 변환을 발견하여, 미셸슨과 몰리의 부정적인 결과를 설명할 수 있게 했다.앙리 푸앵카레(1854–1912)는 로렌츠 변형의 중요성을 지적하고 대중화했다.특히 1905년 아인슈타인의 기사 이전에 발표된 '사이언스와 가설'^[27]에서 열차에 대한 묘사를 찾아볼 수 있다.

로렌츠 변환은 공간 수축과 시간 확장을 예측했다; 1905년까지, 전자는 (전기 성질의) 분자간 힘의 수정으로 인해 에테르에 대해 움직이는 물체의 물리적 수축으로 해석되었다. 반면 후자는 단지 수학적인 ^{[citation needed]}조건이라고 생각되었다.

아인슈타인의 물리학: 시공간

알버트 아인슈타인의 1905년 특수상대성이론은 절대시간이라는 개념에 도전했고, 시간의 선형 흐름을 나타내는 시계의 동기 정의를 공식화했을 뿐이다.

공간 A점에 시계가 있을 경우 A의 관찰자는 A와 동시에 일어나는 손의 위치를 찾아 A의 바로 근처에 있는 사건의 시간 값을 결정할 수 있다.공간의 점 B에 A의 클럭과 유사한 다른 클럭이 있으면 B의 옵서버는 B의 바로 근처에 있는 이벤트의 시간 값을 결정할 수 있다.

그러나 A에서 발생한 사건과 B에서 발생한 사건을 비교하는 것은 더 이상의 가정 없이는 불가능하다.지금까지 우리는 "A time"과 "B time"만을 정의했습니다.

A와 B에 공통의 「시간」을 정의하지 않았다.A에서 B로 이동하는 데 필요한 「시간」이 B에서A로 이동하는 데 필요한 「시간」과 같음을 정의하지 않는 한, 후자는 전혀 정의할 수 없기 때문이다.A에서 B로 향하는 "A time"에서_A 광선을 시작하고 "B time"에서_B A 방향으로 B에 반사되지 않도록 한 후 "A time" t†_A에서 다시 A에 도달한다.

정의에 따라 두 클럭은 다음과 같이 동기화됩니다.

${\displaystyle t_{\text{B}}-t_{\text{\text}A}}=t'_{\text{A}:-t_{\text{B}}{\text{\text}.}}\,\!}$

이 동기 정의에는 모순이 없고 임의의 수의 포인트에 대해 가능하다고 가정합니다.또, 다음의 관계는 일반적으로 유효합니다.

1. B의 클럭이 A의 클럭과 동기화되면 A의 클럭은 B의 클럭과 동기화됩니다.
2. A의 클럭이 B의 클럭 및 C의 클럭과 동기화되면 B와 C의 클럭도 서로 동기화됩니다.

--

아인슈타인은 빛의 속도가 기준 프레임 간에 변하지 않는다면, 속도와 시간은 움직이는 관찰자가 정지된 것과 같은 빛의 속도를 측정하도록 해야 한다는 것을 보여주었다. 왜냐하면 속도는 공간과 시간에 의해 정의되기 때문이다.

${\displaystyle \mathbf{v}}$ ${\displaystyle =}$ ${\displaystyle d\frac{}{}}$ ${\displaystyle \frac{r\mathbf{}}{}}$ ${\displaystyle \frac{d}{}\frac{t}{}}$, \$displaystyle \mathbf {v}$= {$d\mathbf {r} \over dt}{\text{,}}.$ 여기서 r은 위치이고 t는 시간입니다.

실제로 로렌츠 변환(상대 운동에서 x축이 상대 속도 방향으로 향하는 두 기준 프레임의 경우)

전제 조건
대수학 삼각법

${\displaystyle {cases}t'&=\text{여기서 }\text{\timeout {1-v^2}/c^{2}}\x'&timeout(x-timeout)\y'&z'=end{cases}}$

z축을 중심으로 한 유클리드 회전이 x와 y 좌표를 혼합하는 것과 유사한 방식으로 시공간을 "혼합"한다고 할 수 있습니다.이것의 결과는 동시성의 상대성을 포함한다.

보다 구체적으로 로렌츠 변환은 쌍곡선 회전(c(′)′))(cosh ⁡ ϕ − sinh ⁡ ϕ − sinh ⁡ ϕ cosh ⁡ ϕ)(ct))이 ϕ)artanh vc,{\displaystyle{\begin{pmatrix}ct'\\x'\end{pmatrix}}={\begin{pmatrix}\cosh \phi&-\sinh \phi\\-\sinh \phi&\co.쉐 \phi$\end{pmatrix}{\time{pmatrix}ct\x\end{pmatrix}{\text${}}{\$text{}}, 여기서 }}\phi =\operatorname${artanh$},{\frac {v}{c}}{\$text{,}}}}는 ctext{\text{\text{\text{\text{}}}}},},}의 4차원(유클리드 공간에서의 cliclematrix})의 4차원(일반회전이다.y ) (x y ) {$displaystyle { pmatrix }x'\y'\end$ {pmatrix$}=cos$ \theta$&-\sin$ \theta \theta $\end$ {pmatrix}${\cos \theta \end$ {$pmatrix}$는 좌표의 변경에 합니다.)광속 c는 시공간 치수를 서로 다른 단위로 측정하기 때문에 필요한 변환 인자로 볼 수 있다. 미터는 현재 초 단위로 정의되어 있기 때문에 299 792 458 m/s의 정확한 값을 가지고 있다.예를 들어 폭(해리)과 깊이(피트)를 측정한다면 유클리드 공간에서도 비슷한 요소가 필요할 것입니다.물리학에서, 때때로 방정식을 단순화하기 위해 c = 1인 측정 단위가 사용됩니다.

"움직이는" 기준 프레임의 시간은 "정지"에서보다 느리게 실행되는 것으로 다음과 같은 관계에 의해 나타납니다(이것은 "x" = 0, "x" = "t"를 대입하여 로렌츠 변환에 의해 도출될 수 있습니다).

$\displaystyle \Delta t=display\Delta \delta \delta } \over {1-v^{2}/c^{2}}}$

여기서:

• θ는 두 사건이 동일한 장소에서 발생하는 이동 기준 프레임에서 측정된 두 사건 사이의 시간(예: 이동 시계의 두 눈금)으로, 두 사건 사이의 적절한 시간이라고 불린다.
• δt는 이 같은 두 사건 사이의 시간이지만, 정지 기준 프레임에서 측정된다.
• v는 고정된 기준 프레임에 대한 이동 기준 프레임의 속도이다.
• c는 빛의 속도입니다.

따라서 움직이는 물체는 더 느린 시간의 흐름을 보여준다고 한다.이를 시간 연장이라고 합니다.

이러한 변환은 일정한 상대 속도의 2 프레임에만 유효합니다.순진하게 그것들을 다른 상황에 적용하는 것은 쌍둥이 역설과 같은 모순을 낳는다.

그 역설은 예를 들어 아인슈타인의 일반 상대성이론을 사용하여 해결할 수 있습니다. 아인슈타인은 가속된 비관성 기준 프레임의 기하학을 사용합니다.민코프스키 공간을 설명하는 메트릭 텐서를 사용한다.

$\displaystyle \left[(flash^{1}^{2}+(flash^{2})^{2}+(flash^{3})^{2}-c(dt)^2}\right],}$

아인슈타인은 맥스웰 방정식을 보존하는 로렌츠의 변환에 대한 기하학적 해법을 개발했다.그의 필드 방정식은 주어진 시공간 영역에서의 시공간 측정과 그 영역의 에너지 밀도 사이의 정확한 관계를 제공합니다.

아인슈타인의 방정식은 중력장의 존재에 의해 시간이 변화해야 한다고 예측한다(슈바르츠실트 측정법 참조).

${\displaystyle T=frac {dt}{\frac {2}\frcrtGM}{rc^{2}}\right)dt^{2}-{\frac {1}{c^{2}}\left(1-{\frac {2})GM}{rc^{2}}\right)^{-1}dr^{2}-{\frac {r^{2}-{\frac {r^{2}-{\frac {r^{2}}\sin ^{2}\theta \;d\phi ^{2}}}\theta }$

장소:

${\displaystyle T}${\$displaystyle$ T$$$}$는 r {\$displaystyle$ r$\}$ 거리에 있는 물체의 중력 시간 확장입니다.

${\displaystyle d}$ t$\displaystyle dt$는 좌표 시간의 변화 또는 좌표 시간 간격입니다.

$G는$$$중력 상수입니다$.$

$(표시 스타일$ M$)$은 필드를 생성하는 질량입니다.

$display$$-$$GM}{rc^{2}}\right)dt^{2}-{\frac {1}{c^{2}}\left(1-{\frac {2$$})$$GM}{rc^{2}}\right)^{-1}dr^{2}-{\frac {r^2}{c^{2}}d\$theta ^{2}-{\frac {r$^2}{c^{2}}\sin$^{2}\theta \;d$\phi$^2$$$}}}\$$sin$ $display{\displaystyle }$ d표시 스타일의 $변경입니다.$

또는 다음과 같은 간단한 근사치를 사용할 수 있습니다.

${\displaystyle {dt}{d\frac}}=black {1}{\displayrt {1-\leftfrac\frac {2}GM}{rc^{2}}\right}}}}}}.}$

즉, 중력장이 강할수록(따라서 가속도가 클수록) 시간은 더 느리게 흐릅니다.시간 확장에 대한 예측은 움직이는 입자가 덜 에너지적인 입자에 비해 더 느리게 부패하는 입자 가속 실험과 우주선 증거에 의해 확인된다.중력 시간 확장은 중력 적색편이 현상을 일으키고 샤피로 신호는 태양과 같은 거대한 물체 근처에서 시간 지연을 일으킨다.또한 위성 위치 확인 시스템은 이러한 영향을 감안하여 신호를 조정해야 합니다.

아인슈타인의 일반 상대성이론에 따르면 자유롭게 움직이는 입자는 시공간에서 시간을 극대화하는 역사를 더듬는다.이 현상을 최대 노화의 원리라고도 하며, 테일러와 휠러는 다음과 ^[29]같이 설명했습니다.

「극단 노화의 원리:자유물체가 시공간에서 두 사건 사이에서 이동하는 경로는 물체의 손목시계에 기록된 이들 사건 사이의 시간 경과가 극단인 경로입니다."

아인슈타인의 이론은 우주의 모든 점이 '중심'으로 취급될 수 있고, 그에 따라 물리학은 모든 기준 프레임에서 동일하게 작용해야 한다는 가정에 의해 동기 부여되었다.그의 단순하고 우아한 이론은 시간이 관성 프레임에 상대적이라는 것을 보여준다.관성 프레임에서는 뉴턴의 제1법칙이 성립한다.뉴턴은 고유의 국소 기하학이 있기 때문에 공간과 시간을 측정할 수 있다. '범용 시계'는 존재하지 않는다.적어도 두 시스템 간에 동기화 작업을 수행해야 합니다.

양자역학에서의 시간

양자역학 방정식에는 시간 매개변수가 있다.슈뢰딩거^[30] 방정식은

전제 조건
물리 양자 역학

$\displaystyle H(t)\left \psi (t)\right \rangle = i\hbar \left \psi (t)\right \rangle }$

하나의 솔루션이 될 수 있습니다.

${\displaystyle {}_{}{}^{}{}_{}e}$ ${\displaystyle （}$ t${\displaystyle {）}^{}}$ = ${\displaystyle e^{}}$- i ${\displaystyle H^{}}$ t ${\displaystyle {}_{}}$ ${\displaystyle \mathrm{e}}$ $e$ ( 0 )$${\ 、 {$display$ \$psi _$ {$e$ } ( t ) \ $rangle$= $e^$ { - $iHt$/ \ $hbar$} \$psi _${ e } ( 0 )$。$

${\displaystyle {여기}^{}}$서 e${\displaystyle {}^{}}$- ${\displaystyle i^{}}$ ${\displaystyle {Ht}^{}}$ /$${\({$display$e^{-$iHt/\hbar}})$는 시간 진화 연산자, H는 해밀토니안이다.

그러나 위의 슈뢰딩거 그림은 하이젠베르크 그림과 동등하며, 하이젠베르크 그림은 고전역학의 푸아송 괄호와 유사하다.포아송 괄호는 0이 아닌 정류자(예: 관측 가능한 A의 경우 [H,A]) 및 해밀턴 H:

${\displaystyle {\frac {d}{dt}A=(i\hbar)^{-1}[A,H]+\left({\frac {partial t}}\right)_{\mathrm {d}}}}}$

이 방정식은 양자 물리학의 불확도 관계를 나타낸다.예를 들어, 시간(관측 가능한 A)과 함께 에너지 E(해밀턴 H로부터)는 다음을 제공한다.

$\displaystyle \Delta E\geq \frac \hbar } {2}$

어디에

$E(디스플레이$ 스타일\$Delta$E$$)는 에너지의 불확실성입니다.

$T$ ($displaystyle$ \ $Delta$T$$ )는 시간의 불확실성입니다.

$θ(\displaystyle$\hbar$)$는 플랑크의 상수입니다.

일련의 사건의 지속시간을 더 정확하게 측정할수록, 그 시퀀스와 관련된 에너지를 덜 정확하게 측정할 수 있고, 그 반대의 경우도 마찬가지입니다.시간은 양자역학에서 연산자가 아니기 때문에 이 방정식은 표준 불확도 원리와 다르다.

대응하는 정류자 관계도 위의 에너지 및 시간 관계와 유사하게 운동량과 위치의 대응하는 불확도 원리와 함께 서로의 켤레 변수인 운동량 p와 위치 q를 유지한다.

양자역학은 원소의 주기율표의 특성을 설명한다.자기장에서 분자 빔에 대한 오토 스턴과 월터 게라크의 실험을 시작으로, 이시도르 라비 (1898–1988)는 빔의 자기 공명을 변조할 수 있었다.1945년 라비는 이 기술이 원자 빔의 공명 주파수를 사용하는 시계의^[31] 기초가 될 것을 제안했다.2021년 콜로라도 볼더에 있는 JILA의 Jun Ye는 ^[32]중력의 영향을 받아 스트론튬 원자 구름의 꼭대기에서 1mm 높이의 기둥보다 광학 격자 시계 진드기 비율의 차이를 관찰했다.

동적 시스템

동적 시스템 및 카오스 이론, 분산 구조 참조

시간은 시스템의 기하학적 구조를 나타내고 조작할 수 있도록 하는 동적 시스템의 매개변수화라고 할 수 있다.시간은 카오스(즉, 비선형성/반환성)의 암묵적인 결과, 즉 시스템의 정보 엔트로피 생성의 특성 시간 또는 비율이라는 주장이 제기되었다.만델브로는 그의 책 Multifractals와 1/f Noise에서 내적 시간을 소개한다.

시간 결정

Khemani, Moessner 및 Sondhi는 시정을 "안정적이고 보수적이며 거시적인 시계"^{[33]: 7} 로 정의합니다.

시그널링

전제 조건
전기 공학 신호 처리

시그널링은 위에서 설명한 전자파의 한 응용입니다.일반적으로 신호는 당사자와 장소 간의 통신의 일부입니다.예를 들어 나무에 묶인 노란 리본이나 교회 종소리가 있을 수 있습니다.신호는 프로토콜과 관련된 대화의 일부가 될 수 있습니다.또 다른 신호는 도시 시계나 기차역의 시침 위치일 수 있습니다.관심 있는 사람은 그 시계를 보고 시간을 알 수 있습니다.참조: 타임볼은 타임 신호의 초기 형태입니다.

관찰자로서 우리는 과거의 광원뿔 안에서 사는 한 여전히 다른 당과 장소에 신호를 보낼 수 있다.하지만 우리는 그 파티나 과거의 광원뿔 밖에서는 신호를 받을 수 없다.

전자파에 대한 방정식의 공식화와 함께, 통신 분야가 확립될 수 있었다.19세기에는 대륙과 바다에 걸쳐 있는 전기회로가 단순한 점, 대시, 공간 등 코드를 전송할 수 있었다.이것으로부터, 일련의 기술적인 문제가 발생했습니다.카테고리:동기.그러나 우리의 시그널링 시스템은 지터를 제거할 필요가 있는 대략적인 동기 상태, 즉 플레시오크로너스 상태만 가능하다고 해도 무방합니다.

즉, GPS와 같은 기술을 사용하여 시스템을 동기화(엔지니어링 근사치)할 수 있습니다.GPS 위성은 중력과 다른 상대론적 요소들이 회로에 미치는 영향을 설명해야 한다.'셀프 클로킹 신호'를 참조하십시오.

시간 기록 표준 기술

미국의 주요 시간 표준은 현재 레이저 냉각 Cs 분수인 ^[34]NIST-F1로, 암모니아 기반 원자 시계(1949년)에서 세슘 기반 NBS-1(1952년)까지 일련의 시간 및 주파수 표준 중 가장 최신이다.각 클럭의 불확실성은 하루 10,000나노초에서 50년 ^[35]만에 하루 0.5나노초로 감소했습니다.2001년에 NIST-F1의 클럭 불확실성은 0.1나노초/일이었다.점점 더 정확한 주파수 표준의 개발이 진행 중이다.

본 발명의 시간 및 주파수 표준에서는 세슘 원자 집단을 1마이크로켈빈의 온도로 레이저 냉각한다.원자는 각 공간 차원, 수직(위/아래), 수평(왼쪽/오른쪽), 그리고 앞뒤로 6개의 레이저에 의해 형성된 공 모양으로 모입니다.수직 레이저가 세슘 볼을 마이크로파 공동을 통해 밀어냅니다.볼이 냉각되면 세슘 집단이 지면 상태로 냉각되고 위의 두 번째 정의에 명시된 고유 주파수로 빛을 방출합니다.세슘 집단으로부터의 배출에는 11가지 물리적 영향이 설명되며, NIST-F1 클럭에 의해 제어된다.이러한 결과는 BIPM에 보고됩니다.

또, 기준 수소 메서는, TAI(국제 원자시)의 주파수 표준으로서 BIPM에도 보고된다.

시간 측정은 프랑스 세브르에 위치한 BIPM(Bureau International des Poids et Mesures)이 감독하며, 측정의 일관성과 전 세계 SI(International System of Units)에 대한 추적성을 보장합니다.BIPM은 51개 회원국 간의 외교 조약인 미터 협약의 권한 하에 일련의 협의 위원회를 통해 운영되며, 그 구성원은 각각의 국가 도량형 연구소이다.

우주론에서의 시간

일반 상대성 방정식은 비정적 우주를 예측한다.하지만 아인슈타인은 정적 우주만을 받아들였고, 나중에 그의 인생 최대의 실수라고 묘사했던 우주 상수를 더함으로써 이를 반영하기 위해 아인슈타인 장 방정식을 수정했다.하지만 1927년, Georges Lematretre (1894–1966)는 일반 상대성 이론에 근거해, 우주가 원시적인 폭발에서 비롯되었다고 주장했다.그 해 다섯 번째 솔베이 컨퍼런스에서 아인슈타인은 "Vos calculs sont corrects, mais votre physical est abomous."^[36] ("당신의 수학은 맞지만 물리학은 가증스럽다.")라고 일축했다.1929년 에드윈 허블은 팽창하는 우주를 발견했다고 발표했다.현재 일반적으로 받아들여지고 있는 우주론 모델인 람다-CDM 모델은 양의 우주 상수를 가지고 있으며, 따라서 팽창하는 우주뿐만 아니라 가속하는 팽창하는 우주도 가지고 있습니다.

만약 우주가 팽창하고 있었다면, 과거에 훨씬 더 작았을 것이고, 따라서 더 뜨겁고 더 밀도가 높았을 것이다.조지 가모프(1904–1968)는 원소 주기율표에 있는 원소의 풍부함은 뜨겁고 밀도가 높은 우주에서 일어나는 핵 반응에 의해 설명될 수 있다는 가설을 세웠다.그는 '빅뱅'을 비하하기 위해 '빅뱅'이라는 용어를 만든 프레드 호일에 의해 논쟁을 일으켰다.페르미와 다른 사람들은 이 과정이 가벼운 원소만 만들어진 후에 멈췄을 것이고, 따라서 무거운 원소가 풍부하다는 것을 설명하지 못했다고 언급했다.

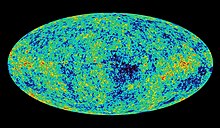
가모프의 예측은 팽창 중에 차가워진 후 우주의 흑체 복사 온도는 5-10켈빈이었다.이것은 1965년 펜지아스와 윌슨에 의해 입증되었다.후속 실험은 빅뱅 후 138억 년 후의 우주의 나이에 해당하는 2.7 켈빈의 온도에 도달했다.

이 극적인 결과는 결국 관측 가능한 가장 작은 시간인 빅뱅의 특이점과 플랑크 시간 사이에 무슨 일이 일어났는지에 대한 문제를 야기했다.시공간 ^[38]폼에서 시간을 분리할 수 있는 경우, 깨진 대칭에 기초한 힌트만 있습니다(자발적 대칭 파괴, 빅뱅의 타임라인 및 카테고리 기사 참조).물리 우주론).

일반상대성이론은 빅뱅에서 시작된 팽창하는 우주에 대한 현대적 개념을 우리에게 주었다.상대성 이론과 양자 이론을 이용하여 우리는 우주의 역사를 대략 재구성할 수 있었다.전자파가 전도체나 전하에 의해 방해받지 않고 전파될 수 있는 우리 시대에는 밤하늘에서 멀리 떨어진 별들을 볼 수 있다. (이 시대 이전에는 우주가 빅뱅 이후 약 37만7천년 후에 전자와 핵이 원자로 결합할 수 있을 만큼 충분히 식기 전에는 w 동안.히치 별빛은 먼 거리에서는 보이지 않았을 것이다.)

응답

일리야 프리고긴의 반복은 "존재보다 시간이 앞선다"이다.뉴턴, 아인슈타인, 양자물리학의 관점과는 대조적으로, 위에서 논의한 바와 같이, 통계학 및 열역학 물리학은 시간의 화살과 빅뱅뿐만 아니라 돌이킬 수 없는 ^[39]현상을 설명할 수 있다고 지적한다.

「 」를 참조해 주세요.

• 상대론적 역학
• 카테고리: 유닛 시스템
• 천문학의 시간

레퍼런스

추가 정보

• 부스타인, 다니엘 J. 발견자.고풍스러운.1985년 2월 12일ISBN 0-394-72625-1
• Dieter Zeh, H. 시간 방향의 물리적 기반.스프링거.ISBN 978-3-540-42081-1
• 과학 혁명의 구조, 쿤, 토마스 S.ISBN 0-226-45808-3
• Mandelbrot, Benott, 멀티프랙탈 및 1/f 노이즈.스프링거 벨락.1999년 2월ISBN 0-387-98539-5
• Prigogine, Ilya(1984년), 혼돈으로부터의 질서.ISBN 0-394-54204-5
• Seres, Michel, et al., "과학, 문화, 시간에 관한 대화(문학과 과학 연구)"1995년 3월ISBN 0-472-06548-3
• 스텐스, 이자벨, 일리야 프리고긴, '이론 아웃 오브 바운더리'미네소타 대학 출판부1997년 11월ISBN 0-8166-2517-4

외부 링크

• Wikimedia Commons의 물리학 시간 관련 미디어