우주의 나이

물리 우주론에서 우주의 나이는 빅뱅 이후 경과된 시간입니다.오늘날, 천문학자들은 우주의 나이 두개의 다른 측정:;[2]과 지역 모드의 관찰에 기초한 측정 측정은 우주의 Lambda-CDM 일치 모델로 2018년의로 해석되는 13.787±0.020 억년의 시대를 가리킨다 이른 상태의 직접적인 관찰에 기반을 둔[1]을 도출했다.불행rn더 어린 ^[3]^[4]^[5]나이를 암시하는 iverse입니다.첫 번째 유형의 측정의 불확실성은 연령에 대해 매우 유사한 수치를 제시한 여러 연구를 바탕으로 2,000만 년으로 좁혀졌다.여기에는 플랑크 우주선, 윌킨슨 마이크로파 이방성 탐사선 및 다른 우주 탐사선에 의한 극초단파 배경 복사에 대한 연구가 포함됩니다.우주 배경 복사 측정은 빅뱅 ^[6]이후 우주의 냉각 시간을 제공하며, 우주의 팽창 속도 측정은 시간을 거꾸로 추정함으로써 대략적인 나이를 계산하는데 사용될 수 있습니다.추정 범위도 우주에서 가장 오래된 별에 대한 추정 범위 내에 있습니다.

설명.

람다-CDM 일치 모델은 약 137억 7천만^[7] 년의 우주 시간 동안 매우 균일하고 뜨겁고 밀도가 높은 원시 상태에서 현재 상태로 우주의 진화를 묘사합니다.이 모델은 이론적으로 잘 이해되고 있으며 WMAP과 같은 최근의 고정밀 천체 관측에 의해 강하게 뒷받침되고 있습니다.이와는 대조적으로, 원시 상태의 기원에 대한 이론은 여전히 매우 추측적이다.

Lambda-CDM 모형을 가장 먼저 잘 이해된 상태에서 역추정하면 순식간에(작은 1초 이내) 특이점에 도달합니다.이것은 "초기 특이점" 또는 "빅뱅 특이점"으로 알려져 있다.이 특이점은 통상적인 의미에서는 물리적 의미를 갖는 것으로 이해되지 않지만, 실제 물리적으로 측정할 수 있는 시간과 일치하지 않더라도 "빅뱅 이후" 측정된 시간을 인용하는 것이 편리하다.

이론적으로는 우주가 더 긴 역사를 가지고 있을 수 있지만, 국제천문연맹은^[8] 현재 람다-CDM 팽창의 지속 시간, 즉 빅뱅 이후 현재 관측 가능한 우주 내에서 경과한 시간을 의미하기 위해 "우주의 나이"라는 용어를 사용하고 있습니다.

관측 한계

우주가 적어도 그 안에서 가장 오래된 것들만큼 나이가 많아야 하기 때문에,^[9]^[10] 우주의 나이에 하한선을 두는 많은 관찰들이 있습니다; 이것들은 다음을 포함합니다.

가장 차가운 백색왜성의 온도는 나이가 들면서 점차 낮아진다.
성단에서 주계열성의 가장 희미한 전환점(낮은 질량의 별은 주계열성에 더 많은 시간을 소비하므로 주계열에서 떨어진 가장 낮은 질량의 별들은 최소 나이를 설정한다.)

우주론적 변수

우주의 나이는 현재 허블 상수를 측정하고 관측된 밀도 매개변수의 값을 사용하여 시간을 추정함으로써 확인할 수 있습니다(

~\Omega ~

{

~\

Omega

~}).

~\Omega ~

암흑 에너지가 발견되기 전에는, 우주가 물질 지배적이라고 믿었습니다.드 시터 우주는 무한한 나이를 가지고 있는 반면 닫힌 우주는 가장 나이가 적습니다.

연령 보정

계수

F ,

{\

displaystyle ~F~}

의

~F~,

값은 현재

분수

물질 밀도 }

~\Omega _{\text{m}}~

~\Omega

_

{\text{m}}~}

과

~\Omega _{\text{m}}~

(와)

~\Omega _{\Lambda }~.

상수

~\Omega _{\Lambda }~.

}

~\Omega _{\Lambda }~.

} . {\

displaystyle

~\

Omega

_

{\

Lambda

}

의

~\Omega _{\Lambda }~.

두 가지 우주론적 매개변수의 함수로 나타난다.파라미터는 왼쪽 상단에 있는 상자로 표시되며, 물질이 지배하는 우주는 오른쪽 하단에 있는 별로 표시됩니다.

우주의 나이를 결정하는 문제는 우주론적 매개변수의 값을 결정하는 문제와 밀접하게 연관되어 있다.오늘날 이것은 우주가 정상 물질, 차가운 암흑 물질, 방사선(광자와 중성미자 둘 다 포함), 그리고 우주 상수를 포함하는 것으로 가정되는 δCDM 모델에서 주로 수행됩니다.

우주의 현재 에너지 밀도에 대한 각각의 부분적 기여는 밀도 매개변수 $~\Omega _{\text{r}}~,$ m $,$ {\ $displaystyle ~\Omega$ $~\Omega _{\text{r}}~,$ _ ${\$ $text$ {m $}~,},}$ $δr$ , ${\displaystyle$ ~\ $Omega$ _ $~\Omega _{\text{r}}~,$ { $~\Omega _{\Lambda }~.$ $}~,}$ 및 $~\Omega _{\Lambda }~.$ 에 $~\Omega _{\Lambda }~.$ 의해 주어진다 $.$ {\ $displaystyle$ ~\ $Omega$ _ ${\Da}.$ 허블 $~H_{0}~$ $~H_{0}~$ 0 $displaystyle ~H_{0$ 과 함께 이 세 매개변수가 가장 중요합니다.

만약 누군가가 이러한 변수들의 정확한 측정치를 가지고 있다면, 우주의 나이는 프리드만 방정식을 사용하여 결정될 수 있다.이 방정식은 스케일 $~a(t)~$ a $(\$ 의 $~a(t)~$ 변화율을 우주의 물질 내용과 관련짓습니다.이 관계를 바꾸면 스케일 팩터의 변화당 시간 변화를 계산하여 이 공식을 통합함으로써 우주의 총 나이를 계산할 수 있습니다. $displaystyle ~t_{0}~)$ 는 다음 $~t_{0}~$ 형식의 표현으로 지정됩니다.

t_{0}=paramfrac {1}{H_{0}}, F(,\Omega _{\text{r}},\Omega _{\text{m}},\Omega _{\Lambda},\dots \,)~

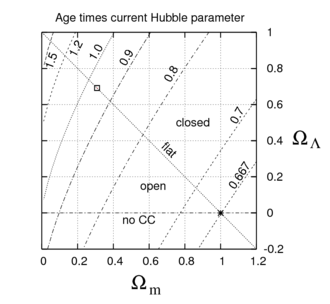
$~H_{0}~$ 서 $~H_{0}~$ 0 $displaystyle ~H_{0}~)$ 은 $~H_{0}~$ 허블 파라미터이고 F $({$ $함수$ 는 $~F~$ 다양한 성분에서 나오는 우주의 에너지 함량에 대한 부분적인 기여에 의존합니다.이 공식에서 얻을 수 있는 첫 번째 관찰은 우주의 나이를 조절하는 허블 매개변수가 물질과 에너지 함량에서 발생하는 보정이라는 것입니다.따라서 우주의 나이는 허블 시간에서 대략적으로 추정할 수 있습니다. 허블 시간은 허블 변수와 반대입니다.허블 시간은 약 69km/s/ $Mpc$ 의 H $~H_{0}~$ 0 $(\displaystyle ~H_{$ 0 $~H_{0}~$ $~1/H_{0}=~$ }~) 값에서 $~1/H_{0}=~$ 1/ $~1/H_{0}=~$ 0 $= {\displaystyle ~$ 1 $/H_$ {0}=~} 145억 ^[11] $~1/H_{0}=~$ 으로 평가됩니다.

정확한 수치를 얻으려면 보정 $함수$ F {\ $displaystyle ~F~}$ 를 $~F~$ 계산해야 합니다.일반적으로 이 작업은 수치적으로 수행되어야 하며, 우주론적 매개 변수 값의 범위에 대한 결과가 그림에 나와 있습니다.플랑크 값 $~(\Omega _{\text{m}},\Omega _{\Lambda })=~$ m $~(\Omega _{\text{m}},\Omega _{\Lambda })=~$ $~(\Omega _{\text{m}},\Omega _{\Lambda })=~$ ) $=$ {\ $~F=0.956~.$ $~(\Omega _{\text{m}},\Omega _{\Lambda })=~$ ~(\ $Omega$ _ ${\text{m}},\Omega$ _ ${\Lambda$ }}) $~(\Omega _{\text{m}},\Omega _{\Lambda })=~$ 0.3086, 0.6914)의 경우, 이 보정 계수는 F $=$ F $~style이다.$ 오른쪽 아래 모서리 $~F={2}/{3}~$ $=$ $~F={2}/{3}~$ / $displaystyle ~$ F={ $2}/{3}~})$ 은 $~F={2}/{3}~$ 훨씬 작기 때문에 허블 매개변수의 고정값으로 볼 때 우주는 더 젊습니다.이 수치를 만들기 위해 $~\Omega _{\text{r}}~$ r {\ $displaystyle$ ~\ $Omega _{\text{$ r}}~}는 $~\Omega _{\text{r}}~$ 일정하게 유지되며(대략 CMB 온도 일정 유지와 동일), 곡률 밀도 파라미터는 나머지 3개의 값으로 고정된다.

플랑크 위성을 제외하고, 윌킨슨 마이크로파 이방성 탐사선(WMAP)은 정확한 숫자를 얻기 위해 다른 측정치를 접어야 하지만 우주의 정확한 나이를 규명하는 데 중요한 역할을 했다.전투 의무 휘장 측정은 문제 콘텐츠Ω m,{\displaystyle ~\Omega_{\text{m}}~,}[12]과 곡률 매개 변수 Ω k.{\displaystyle ~\Omega_{\text{k}}일.}[13]그것은 Ω Λ{\displaystyle ~\Omega_{\Lambda}~ 민감하지 않다}directly,[13]이유 중의 일부를 사기를 구속함에 좋다.stant becom특히 빨간색 시프트가 낮은 경우에만 중요합니다.현재 허블 $~H_{0}~$ $~H_{0}~$ 0 $displaystyle ~H_{0}~)$ 의 $~H_{0}~$ 가장 정확한 측정은 먼 Ia형 초신성의 측정된 밝기와 적색 편이를 통해 이루어진 것으로 추정됩니다.이러한 측정치를 조합하면 위에서 인용한 우주의 나이에 대해 일반적으로 인정받는 값을 얻을 수 있습니다.

우주 상수는 다른 변수들의 고정된 값에 대해 우주를 더 오래되게 만듭니다.우주 상수가 일반적으로 받아들여지기 전에 빅뱅 모형은 허블 매개변수와 물질만 있는 우주로부터 계산한 우주의 ^[14]^[15]나이보다 우리 은하수의 구상 성단이 훨씬 더 오래된 것으로 보이는 이유를 설명하는데 어려움을 겪었기 때문에 이것은 중요하다.우주 상수를 도입함으로써 우주가 이러한 성단보다 더 오래될 수 있을 뿐만 아니라 물질만 있는 우주론 모델이 ^[16]설명할 수 없었던 다른 특징들을 설명할 수 있습니다.

WMAP

NASA의 윌킨슨 극초단파 이방성 탐사선(WMAP) 프로젝트의 2012년 9년간의 데이터 공개는 우주의 나이를 (13772±0.059)×10년⁹ (137억7200만 년, 불확실성 ±5900만 ^[6]년)으로 추정했다.

하지만, 이 나이는 프로젝트의 기본 모델이 정확하다는 가정에 기초하고 있습니다. 우주의 나이를 추정하는 다른 방법들은 다른 나이를 줄 수 있습니다.예를 들어 상대론적 입자의 추가 배경을 가정하면 WMAP 제약조건의 오차 막대를 ^[17]한 단계 더 크게 할 수 있다.

이 측정은 마이크로파 배경 전력 스펙트럼에서 첫 번째 음향 피크의 위치를 사용하여 디커플링 표면의 크기(재결합 시 우주의 크기)를 결정한다.이 표면까지의 빛 이동 시간(사용되는 기하학적 구조에 따라 다름)은 우주에 대한 신뢰할 수 있는 나이를 산출합니다.이 연령을 결정하는 데 사용된 모형의 유효성을 가정하면 잔차 정확도는 거의 1%의 ^[18]오차 한계를 산출합니다.

플랑크

2015년 Planck Collaboration은 우주의 나이를 138억13±0억3800만 년으로 추정했는데, 이는 WMAP ^[19]데이터에서 도출된 초기 수치보다 약간 높지만 불확실한 범위 내에 있다.

아래 표에서 수치는 기준 δCDM 모델의 68% 신뢰 한계 이내입니다.

2015년^[19] 플랑크 결과 우주론적 매개변수

파라미터	기호.	TT + 로우p	TT + 저화질 + 렌즈	TT + 저화질 + 렌즈 + 내선	TT, TE, EE + 로우p	TT, TE, EE + 저화질 + 렌즈	TT, TE, EE + 저화질 + 렌즈 + 내선
우주의 나이 (가)	$t_{0}$	13.813±0.038	13.799±0.038	13.796±0.029	13.813±0.026	13.807±0.026	13.799±0.021
허블 상수 (km c Mpc ）	$H_{0}$	67.31±0.96	67.81±0.92	67.90±0.55	67.27±0.66	67.51±0.64	67.74±0.46

범례:

TT, TE, EE: 플랑크 우주 마이크로파 배경(CMB) 파워 스펙트럼
lowP : 플랑크 편파 데이터 (저전자우도)
렌즈: CMB 렌즈 재구성
ext: 외부 데이터(BAO+JLA+H0).바오: 바리온 음향 진동, JLA: 조인트 광선 곡선 분석, H0: 허블 상수

2018년 Planck Collaboration은 우주의 나이를 137억8700만±^[2]0억2000만년으로 추정했다.

강력한 우선 사항의 가정

우주의 나이를 계산하는 것은 그것을 추정하기 위해 사용되는 모델에 내장된 가정도 정확할 때만 정확합니다.이는 강력한 우선 사항이라고 하며, 기본적으로 모델의 다른 부분에서 잠재적 오류를 제거하여 실제 관측 데이터의 정확성을 최종 결과에 직접 렌더링하는 것을 포함한다.모든 컨텍스트에서 유효한 절차는 아니지만(첨부된 경고: "사용한 기본 모델이 올바르다고 가정한 사실에 근거한다"),^{[citation needed]} 지정된 오류에 대한 경과 시간은 정확합니다(이 오류는 원시 데이터 입력을 모델에 수집하는 데 사용되는 계측기의 오류를 나타냄).

2018년 플랑크 데이터에 가장 적합한 우주의 나이는 137억8700만±0억2000만 년이다.이 수치는 우주의 나이를 정확하게 "직접" 측정한 것입니다(다른 방법에는 일반적으로 허블의 법칙과 구상 성단에서 가장 오래된 별의 나이 등이 포함됩니다).같은 파라미터(이 경우는 우주의 나이)를 결정하기 위해 다른 방법을 사용하여 "오류"에 중복되지 않고 다른 답을 얻을 수 있습니다.문제를 가장 잘 피하기 위해 두 세트의 불확실성을 보여주는 것이 일반적입니다. 하나는 실제 측정과 관련된 것이고 다른 하나는 사용 중인 모델의 시스템 오류와 관련된 것입니다.

따라서 (플랑크의) 우주의 나이를 결정하는 데 사용되는 데이터의 분석에서 중요한 요소는 베이지안 통계 분석을 사용하는 것이다. 베이지안 통계 분석은 이전 단계(즉, 모델)^[18]에 기초하여 결과를 정규화하는 것이다.이는 사용된 ^[20]^[21]특정 모델로 인한 측정 정확도의 불확실성을 수량화합니다.

역사

네이처 타임라인

−13 —

–

−12 —

–

−11 —

–

−10 —

–

−9 —

–

−8 —

–

−7 —

–

−6 —

–

−5 —

–

−4 —

–

−3 —

–

−2 —

–

−1 —

–

0 —

←

←

←

←

←

←

←

←

←

←

←

←

←

←

←

←

←

←

←

초기 유인원/인간

L
i
f
e

(억 년 전)

18세기에 지구의 나이가 수십억은 아니더라도 수백만 년이라는 개념이 나타나기 시작했다.하지만, 19세기 전반과 20세기 전반의 대부분의 과학자들은 우주 자체가 정상 상태이고 영원한 상태이며, 아마도 별이 오고 가는 것으로 추정했지만,^{[citation needed]} 그 당시에 알려진 가장 큰 규모의 변화는 일어나지 않았다.

우주의 나이가 유한할 수 있다는 것을 보여주는 첫 번째 과학 이론은 19세기 중반에 공식화된 열역학 연구였다.엔트로피의 개념은 만약 우주가 무한히 오래되었다면, 내부의 모든 것은 같은 온도에 있을 것이고, 따라서 별도 생명도 없을 것이라고 지시한다.그 당시에는 이 모순에 대한 과학적 설명이 제시되지 않았다.

1915년 알버트 아인슈타인은 일반상대성이론을^[22] 발표했고 1917년 그의 이론을 바탕으로 최초의 우주론 모델을 만들었다.정상 상태의 우주와 일관성을 유지하기 위해 아인슈타인은 나중에 우주 상수라고 불리는 것을 그의 방정식에 추가했다.아인슈타인의 정적 우주 모델은 아서 에딩턴에 의해 불안정하다는 것을 증명했다.

우주가 정적이 아니라 팽창하고 있다는 첫 번째 직접적인 관측 암시는 ^[23]1929년 에드윈 허블이 발표한 연구에서 베스토 슬리퍼에 의해 주로 관측된 '후퇴 속도'와 '은하'까지의 거리를 결합함으로써 나왔다.20세기 초, 허블과 다른 천체들은 특정 성운 안에 있는 개별 별들을 분해하여, 그것들이 우리 은하수 은하와 비슷하지만 외부에 있는 은하라는 결론을 내렸습니다.게다가, 이 은하들은 매우 크고 매우 멀리 떨어져 있었다.이 먼 은하들을 촬영한 스펙트럼은 도플러 효과로 추정되는 스펙트럼 라인의 붉은 변화를 보여주었고, 따라서 이 은하들이 지구로부터 멀어지고 있음을 나타냅니다.게다가 이 은하들이 멀리 있을수록(더 어둡게 보일수록) 적색편이도 커졌고, 따라서 더 빨리 멀어지는 것처럼 보였습니다.이것은 우주가 정적이 아니라 팽창하고 있다는 최초의 직접적인 증거였다.우주의 나이에 대한 첫 번째 추정치는 모든 물체가 같은 지점에서 언제 속도를 내기 시작했는지에 대한 계산에서 나왔다.은하들이 나중에 발견된 은하들보다 훨씬 더 가까운 것으로 추정되었기 때문에 우주의 나이에 대한 허블의 초기 값은 매우 낮았습니다.

현재 허블 상수로 알려진 수치인 우주의 팽창 속도를 합리적으로 정확하게 측정한 것은 1958년 천문학자 앨런 샌디지에 ^[24]의해 처음 이루어졌다.허블 상수에 대한 그의 측정값은 오늘날 일반적으로 받아들여지는 값 범위에 매우 근접했습니다.

그러나 Sandage는 아인슈타인과 마찬가지로 발견 당시 자신의 결과를 믿지 않았다.샌디지는 이 차이를 설명하기 위해 우주론에 대한 새로운 이론을 제안했다.이 문제는 별의 나이를 추정하는 데 사용된 이론적인 모형의 개선으로 다소 해결되었다.2013년 현재, 가장 오래된 것으로 알려진 별의 나이는 144억6±08억 ^[25]년이다.

1965년에 발표된^[26] 극초단파 우주 배경 방사선의 발견은 마침내 팽창하는 우주에 대한 과학적 불확실성에 대한 효과적인 종말을 가져왔다.그것은 60마일도 채 떨어지지 않은 두 팀이 일한 우연한 결과였다.1964년, Arno Penzias와 Robert Wilson은 초감응 안테나를 사용하여 전파 에코를 탐지하려고 했습니다.안테나는 하늘에 고르게 퍼져 밤낮으로 존재하는 마이크로파 영역에서 낮고 안정적인 미스터리한 노이즈를 지속적으로 감지했습니다.실험 후, 그들은 그 신호가 지구, 태양, 또는 우리 은하에서 온 것이 아니라 우리 은하 밖에서 온 것이라는 것을 확신했지만, 그것을 설명할 수는 없었다.동시에, 다른 팀인 로버트 H. 딕, 짐 피블스, 그리고 데이비드 윌킨슨은 빅뱅으로부터 남겨질 수 있는 낮은 수준의 소음을 감지하려고 시도하고 있었고 빅뱅 이론이 맞는지 증명할 수 있었다.두 팀은 검출된 소음이 사실상 빅뱅으로부터 남겨진 방사능이며, 이것이 이론이 옳다는 강력한 증거라는 것을 깨달았다.그 이후로, 많은 다른 증거들이 이 결론을 강화하고 확인했으며, 우주의 추정 나이를 현재의 수치로 수정했습니다.

2001년 발사된 우주탐사선 WMAP과 2009년 발사된 플랑크는 허블 상수와 은하 거리에 관계없이 우주의 나이를 측정하는 데이터를 만들어 가장 큰 ^[18]오차원을 제거했다.

「」를 참조해 주세요.

레퍼런스

^ "From an almost perfect Universe to the best of both worlds". Planck mission. sci.esa.int. European Space Agency. 17 July 2018. last paragraphs. Archived from the original on 13 April 2020.
^ ^a ^b Planck Collaboration (2020). "Planck 2018 results. VI. Cosmological parameters". Astronomy & Astrophysics. 641. page A6 (see PDF page 15, Table 2: "Age/Gyr", last column). arXiv:1807.06209. doi:10.1051/0004-6361/201833910. S2CID 119335614.
^ Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; Bucciarelli, Beatrice; Lattanzi, Mario G.; et al. (2018-07-12). "Milky Way cepheid standards for measuring cosmic distances and application to Gaia DR2: Implications for the Hubble constant". The Astrophysical Journal. 861 (2): 126. arXiv:1804.10655. Bibcode:2018ApJ...861..126R. doi:10.3847/1538-4357/aac82e. ISSN 1538-4357. S2CID 55643027.
^ ESA/Planck Collaboration (17 July 2018). "Measurements of the Hubble constant". sci.esa.int. European Space Agency. Archived from the original on 7 October 2020.
^ Freedman, Wendy L.; Madore, Barry F.; Hatt, Dylan; Hoyt, Taylor J.; Jang, In-Sung; Beaton, Rachael L.; et al. (2019-08-29). "The Carnegie-Chicago Hubble Program. VIII. An independent determination of the Hubble constant based on the tip of the red giant branch". The Astrophysical Journal. 882 (1): 34. arXiv:1907.05922. Bibcode:2019ApJ...882...34F. doi:10.3847/1538-4357/ab2f73. ISSN 1538-4357. S2CID 196623652.
^ ^a ^b Bennett, C.L.; et al. (2013). "Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Final maps and results". The Astrophysical Journal Supplement Series. 208 (2): 20. arXiv:1212.5225. Bibcode:2013ApJS..208...20B. doi:10.1088/0067-0049/208/2/20. S2CID 119271232.
^ "Cosmic Detectives". European Space Agency. 2 April 2013. Retrieved 2013-04-15.
^ Chang, K. (9 March 2008). "Gauging age of universe becomes more precise". The New York Times.
^ Chaboyer, Brian (1 December 1998). "The age of the universe". Physics Reports. 307 (1–4): 23–30. arXiv:astro-ph/9808200. Bibcode:1998PhR...307...23C. doi:10.1016/S0370-1573(98)00054-4. S2CID 119491951.
^ Chaboyer, Brian (16 February 1996). "A Lower Limit on the Age of the Universe". Science. 271 (5251): 957–961. arXiv:astro-ph/9509115. Bibcode:1996Sci...271..957C. doi:10.1126/science.271.5251.957. S2CID 952053.
^ Liddle, A. R. (2003). An Introduction to Modern Cosmology (2nd ed.). Wiley. p. 57. ISBN 978-0-470-84835-7.
^ Hu, W. "Animation: Matter Content Sensitivity. The matter-radiation ratio is raised while keeping all other parameters fixed". University of Chicago. Archived from the original on 23 February 2008. Retrieved 2008-02-23.
^ ^a ^b Hu, W. "Animation: Angular diameter distance scaling with curvature and lambda". University of Chicago. Archived from the original on 23 February 2008. Retrieved 2008-02-23.
^ "Globular Star Clusters". SEDS. 1 July 2011. Archived from the original on 24 February 2008. Retrieved 2013-07-19.
^ Iskander, E. (11 January 2006). "Independent age estimates". University of British Columbia. Archived from the original on 6 March 2008. Retrieved 2008-02-23.
^ Ostriker, J.P.; Steinhardt, P.J. (1995). "Cosmic concordance". arXiv:astro-ph/9505066.
^ de Bernardis, F.; Melchiorri, A.; Verde, L.; Jimenez, R. (2008). "The Cosmic Neutrino Background and the Age of the Universe". Journal of Cosmology and Astroparticle Physics. 2008 (3): 20. arXiv:0707.4170. Bibcode:2008JCAP...03..020D. doi:10.1088/1475-7516/2008/03/020. S2CID 8896110.
^ ^a ^b ^c Spergel, D.N.; et al. (2003). "First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters". The Astrophysical Journal Supplement Series. 148 (1): 175–194. arXiv:astro-ph/0302209. Bibcode:2003ApJS..148..175S. doi:10.1086/377226. S2CID 10794058.
^ ^a ^b Planck Collaboration (2016). "Planck 2015 results. XIII. Cosmological parameters". Astronomy & Astrophysics. 594. page A13 (see PDF page 32, Table 4: "Age/Gyr", last column). arXiv:1502.01589. Bibcode:2016A&A...594A..13P. doi:10.1051/0004-6361/201525830. S2CID 119262962.
^ Loredo, T. J. (1992). "The Promise of Bayesian Inference for Astrophysics" (PDF). In Feigelson, E. D.; Babu, G. J. (eds.). Statistical Challenges in Modern Astronomy. Springer-Verlag. pp. 275–297. Bibcode:1992scma.conf..275L. doi:10.1007/978-1-4613-9290-3_31. ISBN 978-1-4613-9292-7.
^ Colistete, R.; Fabris, J. C.; Concalves, S. V. B. (2005). "Bayesian statistics and parameter constraints on the generalized Chaplygin gas model Using SNe ia data". International Journal of Modern Physics D. 14 (5): 775–796. arXiv:astro-ph/0409245. Bibcode:2005IJMPD..14..775C. doi:10.1142/S0218271805006729. S2CID 14184379.
^ Einstein, A. (1915). "Zur allgemeinen Relativitätstheorie" [On the general theory of relativity]. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (in German): 778–786. Bibcode:1915SPAW.......778E.
^ Hubble, E. (1929). "A relation between distance and radial velocity among extra-galactic nebulae". Proceedings of the National Academy of Sciences. 15 (3): 168–173. Bibcode:1929PNAS...15..168H. doi:10.1073/pnas.15.3.168. PMC 522427. PMID 16577160.
^ Sandage, A. R. (1958). "Current Problems in the Extragalactic Distance Scale". The Astrophysical Journal. 127 (3): 513–526. Bibcode:1958ApJ...127..513S. doi:10.1086/146483.
^ Bond, H. E.; Nelan, E. P.; Vandenberg, D. A.; Schaefer, G. H.; Harmer, D. (2013). "HD 140283: A Star in the Solar Neighborhood that Formed Shortly After the Big Bang". The Astrophysical Journal. 765 (12): L12. arXiv:1302.3180. Bibcode:2013ApJ...765L..12B. doi:10.1088/2041-8205/765/1/L12. S2CID 119247629.
^ Penzias, A. A.; Wilson, R .W. (1965). "A Measurement of Excess Antenna Temperature at 4080 Mc/s". The Astrophysical Journal. 142: 419–421. Bibcode:1965ApJ...142..419P. doi:10.1086/148307.

외부 링크

Wright, Ned. "Cosmology tutorial". Division of Astronomy & Astrophysics (academic personal site). University of California, Los Angeles.

Wright, Edward L. (2 July 2005). "Age of the Universe". Division of Astronomy & Astrophysics (academic personal site). University of California, Los Angeles.

Hu, Wayne. "cosmological parameter animations" (academic personal site). U. Chicago.

Ostriker, J.P.; Steinhardt, P.J. (1995). "Cosmic concordance". arXiv:astro-ph/9505066.

"Globular star clusters". SEDS. Archived from the original on 2015-04-30.

Scott, Douglas. "Independent age estimates" (academic personal site). Vancouver, BC: University of British Columbia.

"The scale of the universe". KryssTal. - 초보자용 공간 및 시간 설정.

"Cosmology calculator (with graph generation)". iCosmos.

"The Expanding Universe". American Institute of Physics.

[1] "From an almost perfect Universe to the best of both worlds". Planck mission. sci.esa.int. European Space Agency. 17 July 2018. last paragraphs. Archived from the original on 13 April 2020.

[Planck_2018-2] Planck Collaboration (2020). "Planck 2018 results. VI. Cosmological parameters". Astronomy & Astrophysics. 641. page A6 (see PDF page 15, Table 2: "Age/Gyr", last column). arXiv:1807.06209. doi:10.1051/0004-6361/201833910. S2CID 119335614.

[3] Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; Bucciarelli, Beatrice; Lattanzi, Mario G.; et al. (2018-07-12). "Milky Way cepheid standards for measuring cosmic distances and application to Gaia DR2: Implications for the Hubble constant". The Astrophysical Journal. 861 (2): 126. arXiv:1804.10655. Bibcode:2018ApJ...861..126R. doi:10.3847/1538-4357/aac82e. ISSN 1538-4357. S2CID 55643027.

[4] ESA/Planck Collaboration (17 July 2018). "Measurements of the Hubble constant". sci.esa.int. European Space Agency. Archived from the original on 7 October 2020.

[5] Freedman, Wendy L.; Madore, Barry F.; Hatt, Dylan; Hoyt, Taylor J.; Jang, In-Sung; Beaton, Rachael L.; et al. (2019-08-29). "The Carnegie-Chicago Hubble Program. VIII. An independent determination of the Hubble constant based on the tip of the red giant branch". The Astrophysical Journal. 882 (1): 34. arXiv:1907.05922. Bibcode:2019ApJ...882...34F. doi:10.3847/1538-4357/ab2f73. ISSN 1538-4357. S2CID 196623652.

[arxiv-20121220-6] Bennett, C.L.; et al. (2013). "Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Final maps and results". The Astrophysical Journal Supplement Series. 208 (2): 20. arXiv:1212.5225. Bibcode:2013ApJS..208...20B. doi:10.1088/0067-0049/208/2/20. S2CID 119271232.

[7] "Cosmic Detectives". European Space Agency. 2 April 2013. Retrieved 2013-04-15.

[8] Chang, K. (9 March 2008). "Gauging age of universe becomes more precise". The New York Times.

[9] Chaboyer, Brian (1 December 1998). "The age of the universe". Physics Reports. 307 (1–4): 23–30. arXiv:astro-ph/9808200. Bibcode:1998PhR...307...23C. doi:10.1016/S0370-1573(98)00054-4. S2CID 119491951.

[10] Chaboyer, Brian (16 February 1996). "A Lower Limit on the Age of the Universe". Science. 271 (5251): 957–961. arXiv:astro-ph/9509115. Bibcode:1996Sci...271..957C. doi:10.1126/science.271.5251.957. S2CID 952053.

[11] Liddle, A. R. (2003). An Introduction to Modern Cosmology (2nd ed.). Wiley. p. 57. ISBN 978-0-470-84835-7.

[12] Hu, W. "Animation: Matter Content Sensitivity. The matter-radiation ratio is raised while keeping all other parameters fixed". University of Chicago. Archived from the original on 23 February 2008. Retrieved 2008-02-23.

[anim3-13] Hu, W. "Animation: Angular diameter distance scaling with curvature and lambda". University of Chicago. Archived from the original on 23 February 2008. Retrieved 2008-02-23.

[14] "Globular Star Clusters". SEDS. 1 July 2011. Archived from the original on 24 February 2008. Retrieved 2013-07-19.

[15] Iskander, E. (11 January 2006). "Independent age estimates". University of British Columbia. Archived from the original on 6 March 2008. Retrieved 2008-02-23.

[16] Ostriker, J.P.; Steinhardt, P.J. (1995). "Cosmic concordance". arXiv:astro-ph/9505066.

[17] Bernardis, F.; Melchiorri, A.; Verde, L.; Jimenez, R. (2008). "The Cosmic Neutrino Background and the Age of the Universe". Journal of Cosmology and Astroparticle Physics. 2008 (3): 20. arXiv:0707.4170. Bibcode:2008JCAP...03..020D. doi:10.1088/1475-7516/2008/03/020. S2CID 8896110.

[wmap-18] Spergel, D.N.; et al. (2003). "First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters". The Astrophysical Journal Supplement Series. 148 (1): 175–194. arXiv:astro-ph/0302209. Bibcode:2003ApJS..148..175S. doi:10.1086/377226. S2CID 10794058.

[Planck_2015-19] Planck Collaboration (2016). "Planck 2015 results. XIII. Cosmological parameters". Astronomy & Astrophysics. 594. page A13 (see PDF page 32, Table 4: "Age/Gyr", last column). arXiv:1502.01589. Bibcode:2016A&A...594A..13P. doi:10.1051/0004-6361/201525830. S2CID 119262962.

[20] Loredo, T. J. (1992). "The Promise of Bayesian Inference for Astrophysics" (PDF). In Feigelson, E. D.; Babu, G. J. (eds.). Statistical Challenges in Modern Astronomy. Springer-Verlag. pp. 275–297. Bibcode:1992scma.conf..275L. doi:10.1007/978-1-4613-9290-3_31. ISBN 978-1-4613-9292-7.

[21] Colistete, R.; Fabris, J. C.; Concalves, S. V. B. (2005). "Bayesian statistics and parameter constraints on the generalized Chaplygin gas model Using SNe ia data". International Journal of Modern Physics D. 14 (5): 775–796. arXiv:astro-ph/0409245. Bibcode:2005IJMPD..14..775C. doi:10.1142/S0218271805006729. S2CID 14184379.

[22] Einstein, A. (1915). "Zur allgemeinen Relativitätstheorie" [On the general theory of relativity]. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (in German): 778–786. Bibcode:1915SPAW.......778E.

[23] Hubble, E. (1929). "A relation between distance and radial velocity among extra-galactic nebulae". Proceedings of the National Academy of Sciences. 15 (3): 168–173. Bibcode:1929PNAS...15..168H. doi:10.1073/pnas.15.3.168. PMC 522427. PMID 16577160.

[24] Sandage, A. R. (1958). "Current Problems in the Extragalactic Distance Scale". The Astrophysical Journal. 127 (3): 513–526. Bibcode:1958ApJ...127..513S. doi:10.1086/146483.

[arxiv-25] Bond, H. E.; Nelan, E. P.; Vandenberg, D. A.; Schaefer, G. H.; Harmer, D. (2013). "HD 140283: A Star in the Solar Neighborhood that Formed Shortly After the Big Bang". The Astrophysical Journal. 765 (12): L12. arXiv:1302.3180. Bibcode:2013ApJ...765L..12B. doi:10.1088/2041-8205/765/1/L12. S2CID 119247629.

[apj142:419-26] Penzias, A. A.; Wilson, R .W. (1965). "A Measurement of Excess Antenna Temperature at 4080 Mc/s". The Astrophysical Journal. 142: 419–421. Bibcode:1965ApJ...142..419P. doi:10.1086/148307.

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[14]

[15]

[16]

[17]

[18]

[19]

[2]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

v t 우주론
배경	우주의 나이 빅뱅 우주의 연대기 우주 관측 가능한 우주
이력 우주론	우주 마이크로파 배경 발견 빅뱅 이론의 역사 빅뱅에 대한 종교적 해석 우주론 연대표
과거 우주	우주 마이크로파 배경 우주 중성미자 배경 중력파 배경 인플레이션 핵합성 거주 가능 시대
현재 우주	FLRW 메트릭 프리드만 방정식 허블의 법칙 공간의 메트릭 확장 확장 가속화 레드시프트
미래 우주	팽창하는 우주의 미래 우주의 궁극적 운명
구성 요소들	암흑 에너지 다크 유체 암흑 물질 람다-CDM 모형
구조 형성	은하 필라멘트 은하 형성 큰 퀘이사군 대규모 구조물 이온화 우주의 모양 구조 형성
실험	2dF 화씨 6도 부메랑 코베 일러스트리스 프로젝트 관측 우주론 플랑크 SDSS WMAP
천문 포털

Search

우주의 나이

네임스페이스

더

목차

설명.

관측 한계

우주론적 변수

WMAP

플랑크

강력한 우선 사항의 가정

역사

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

우주의 나이

설명.

관측 한계

우주론적 변수

WMAP

플랑크

강력한 우선 사항의 가정

역사

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.