특수 상대성 검정

Tests of special relativity

특수상대성이론은 중력이 중요하지 않은 한 모든 물리적 현상을 설명하는 데 근본적인 역할을 하는 물리 이론이다.많은 실험들이 그것의 개발과 정당화에 중요한 역할을 했다.이 이론의 강점은 매우 다양한 실험의 결과를 정밀하게 정확하게 예측할 수 있는 독특한 능력에 있다.플랑크 척도나 중성미자 영역과 같은 효과에 초점을 맞춘 현대 실험은 여전히 꾸준히 정밀도를 높여 진행되고 있다.그들의 결과는 특수 상대성 이론의 예측과 일치한다.다양한 테스트 컬렉션은 Jakob [1]Laub,[2][3] Zhang, Mattingly, Clifford [4]Will 및 Roberts/Schleif에 [5]의해 제공되었습니다.

특수상대성이론은 평탄한 시공간, 즉 중력의 큰 영향을 받지 않는 모든 현상으로 제한된다.후자는 일반 상대성 이론의 영역에 있으며 일반 상대성 이론의 해당 테스트를 고려해야 한다.

상대성 이론으로 가는 길을 닦는 실험

19세기 빛의 지배적인 이론은 빛이 공기를 통해 소리가 전파되는 방식과 유사한 방식으로 전파되는 고정된 매체인 발광 에테르 이론이었다.유추하자면, 빛의 속도는 에테르 내 모든 방향에서 일정하며 광원의 속도와 무관합니다.따라서 에테르에 대해 상대적으로 움직이는 관찰자는 공기에 대해 움직이는 관찰자가 겉으로 보이는 바람을 측정하더라도 어떤 종류의 "에테르 바람"을 측정해야 한다.

1차 실험

주요 기사:발광 에테르 § 1차 실험
피조 실험, 1851년

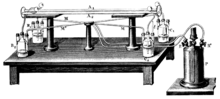
프랑수아 아라고(1810)의 작업을 시작으로 일련의 광학 실험이 수행되었고, 이는 v/c에서 1차 크기에서 양의 결과를 얻어야 했고, 따라서 에테르의 상대적 움직임을 입증해야 했다.하지만 결과는 부정적이었다.오거스틴 프레넬(1818)은 물질이 에테르를 약간 끌어당기고 있다는 보조 가설, 소위 "끌림 계수"의 도입과 함께 설명을 제공했습니다.이 계수는 피조 실험(1851)에 의해 직접적으로 입증되었다.이 계수로 인해 모든 1차 광학 실험은 반드시 음의 결과를 내야 한다는 것이 나중에 밝혀졌다.또한 일부 정전기 1차 실험이 실시되어 다시 음성 결과가 나왔다.일반적으로 헨드릭 로렌츠(1892년, 1895년)는 왜 모든 1차 광학 및 정전기 실험이 null 결과를 낳았는지를 증명하면서 움직이는 관찰자를 위한 몇 가지 새로운 보조 변수를 도입했다.예를 들어, 로렌츠는 정전장이 운동선에서 수축하는 위치 변수와 움직이는 관측자의 시간 좌표가 현재 위치에 [1]따라 달라지는 또 다른 변수("로컬 타임")를 제안했다.

이차 실험

주요 기사:발광 에테르 second 2차 실험
마이클슨 몰리 간섭계

그러나 정상 에테르 이론은 실험이 v/c 단위로 2차 크기를 측정할 수 있을 정도로 정밀할 때 긍정적인 결과를 제공할 것이다.앨버트 A. 마이클슨은 1881년에 이런 종류의 첫 번째 실험을 했고, 1887년에 더 정교한 마이클슨-몰리 실험을 했다.서로 다른 방향으로 한동안 이동하는 두 개의 광선이 간섭을 일으키기 때문에 에테르 바람과 관련된 다른 방향이 간섭 프링의 변위로 이어집니다.하지만 결과는 다시 부정적이었다.이 딜레마에서 벗어나는 방법은 물질이 에테르(길이 수축)에 대해 운동선상에서 수축한다는 조지 프란시스 피츠제럴드(1889)와 로렌츠(1892)의 제안이었다.즉, 정전장 수축에 대한 오래된 가설은 분자간 힘으로 확장되었다.그러나 이에 대한 이론적 이유가 없었기 때문에 수축 가설은 임시 가설로 간주되었다.

광학적 Michelson-Morley 실험 외에, 전기 역학적 등가물인 Trouton-Noble 실험도 수행되었다.이를 통해 움직이는 콘덴서가 토크를 받아야 한다는 것을 입증해야 한다.또한, Rayleigh and Breas 실험에서는 예를 들어 복굴절로 이어진다는 가정과 같이 실험실 프레임에서 길이 수축의 일부 결과를 측정하고자 했습니다.이 모든 실험들이 음성적인 결과로 이어졌지만 (1908년에 실시된 트라우톤-랭킨 실험에서도 길이 수축이 전자 코일에 미치는 영향을 측정했을 때 음성적인 결과가 나왔다.)[1]

1904년 이전에 수행된 모든 실험을 설명하기 위해, 로렌츠는 완전한 로렌츠 변환을 도입함으로써 그의 이론을 다시 확장해야 했다.앙리 푸앵카레는 1905년 절대 운동(상대성 원리)을 나타내는 것이 불가능하다는 것은 명백한 자연의 법칙이라고 선언했다.

완전한 에테르 항력에 대한 반박

주요 기사:에테르 항력 가설
로지의 에테르 기계.그 강철 원반의 지름은 1야드였다.흰 빛은 빔 스플리터에 의해 분할되어 기구 주위를 세 번 돌고 나서 다시 합쳐져 테두리를 형성했다.

부정적인 에테르 드리프트 실험을 설명할 수 있는 에테르를 지구 안이나 근처에서 완전히 끌어당길 수 있다는 생각은 다양한 실험들에 의해 반박되었다.

  • Oliver Lodge(1893)는 민감한 공통 경로 간섭계 배열 위아래로 빠르게 회전하는 강철 디스크가 측정 가능한 프린지 시프트를 생성하지 못했다는 것을 발견했다.
  • Gustaf Hammar(1935)는 공통 경로 간섭계를 사용하여 에테르를 끌어당겼다는 증거를 찾지 못했다. 한 팔은 납으로 막힌 두꺼운 파이프로 둘러싸인 반면 다른 팔은 자유로웠다.
  • Sagnac 효과는 토류 항력에 의한 에테르풍은 입증할 수 없다는 것을 보여주었다.
  • 빛의 수차의 존재는 에테르 항력 가설과 일치하지 않았다.
  • 에테르 항력은 질량에 비례하여 지구 전체에 대해서만 발생한다는 가정은 지구의 운동을 통한 사냐크 효과를 입증한 Michelson-Gale-Pearson 실험에 의해 반박되었다.

로지는 물리학자들이 다음과 같은 역설적인 상황을 표현했다: "실용 가능한 속도로는 에테르에 대한 현저한 점착력이 중요하지 않다.원자는 충분한 속도로 진동하거나 회전할 경우 진동할 수 있어야 합니다.그렇지 않으면 빛이나 어떤 종류의 복사도 방출하지 않습니다.그러나 어떤 경우에도 원자는 그것을 끌고 가거나 그것을 [6]통해 균일한 운동으로 저항하는 것처럼 보이지 않습니다."

특수상대성이론

개요

결국, 알버트 아인슈타인(1905)은 그 당시에 알려진 확립된 이론과 사실들은 공간과 시간의 개념이 근본적인 수정의 대상이 될 때만 논리적인 일관성 있는 체계를 형성한다는 결론을 도출했다.예:

  • 맥스웰-로렌츠의 전기역학(광속으로부터 광속으로부터 독립),
  • 음의 에테르 드리프트 실험(우선 기준 프레임 없음),
  • 이동 자석 및 도체 문제(상대 운동만 해당),
  • 피조 실험과 빛의 수차(둘 다 수정된 속도 추가와 완전한 에테르 항력이 없음을 의미)

그 결과는 특수 상대성 이론으로, 모든 관성 기준 프레임에서 빛의 속도의 항상성과 상대성 원리에 기초합니다.여기서 로렌츠 변환은 더 이상 단순한 보조 가설의 집합이 아니라 기본적인 로렌츠 대칭을 반영하며 양자 전기역학 같은 성공적인 이론의 기초를 형성합니다.특수상대성이론은 다음과 [7]같은 많은 검정 가능한 예측을 제공합니다.

상대성 원리 광속의 항상성 시간 연장
관성 프레임에서 균일하게 움직이는 관찰자는 공동 움직이는 실험 배열에 의해 그의 "절대" 운동 상태를 결정할 수 없습니다. 모든 관성 프레임에서 측정된 빛의 속도는 선원의 속도와 무관하며 모든 방향(등방성)에서 동일하며, 무거운 물체에 의해 도달할 수 없다. 관성 프레임에서 정지 상태의 두 동기 클럭 A와 B 사이를 이동하는 클럭 C(= 주기적 프로세스)의 속도는 두 클럭에 대해 지연됩니다.
또한 길이 수축, 도플러 효과, 수차 및 표준 모형과 같은 상대론적 이론의 실험적 예측과 같은 다른 상대론적 효과도 측정할 수 있습니다.

기초 실험

케네디–가시 다이크 실험

특수상대성이론의 효과는 현상학적으로 다음의 세 가지 기본 [8]실험에서 도출할 수 있다.

  • 측정 장치의 방향에 대한 빛의 속도의 의존성을 테스트할 수 있는 Michelson-Morley 실험.그것은 움직이는 물체의 세로 길이와 가로 길이 사이의 관계를 확립한다.
  • 측정 장치의 속도에 대한 빛의 속도의 의존성을 테스트할 수 있는 케네디-손다이크 실험.종방향 길이와 이동 물체의 지속시간 사이의 관계를 확립한다.
  • Ives – Stilwell 실험. 이때까지 확장은 직접 테스트할 수 있습니다.

이 세 가지 실험으로부터 그리고 푸앵카레-아인슈타인 동기화를 사용함으로써 완전한 로렌츠 변환이 이루어지며, / - v / 2 (\= 1 / {\ - / 가 로렌츠 [8]인자가 된다.

로렌츠 변환의 파생 외에도, 이러한 실험의 조합은 개별적으로 볼 때 다른 방식으로 해석될 수 있기 때문에 중요하다.예를 들어, Michelson-Morley와 같은 등방성 실험은 상대성 원리의 단순한 결과로 볼 수 있으며, 이에 따라 관성적으로 움직이는 관찰자는 자신을 정지상태로 간주할 수 있다.따라서, MM 실험은 그 자체로 방출 이론이나 완전한 에테르 항력 가설과 같은 갈릴레오 불변 이론과 양립할 수 있으며, 이것은 또한 일종의 상대성 원리를 포함하고 있다.하지만, 갈릴레오 불변 이론들을 배제하는 다른 실험들이 고려될 때(예: 이브-스틸웰 실험, 방출 이론의 다양한 반박들, 그리고 완전한 에테르 끌림의 반박들), 로렌츠 불변 이론들과 따라서 특수 상대성 이론들이 유일하게 실행 가능한 이론들이다.

광속의 항상성

간섭계, 공진기

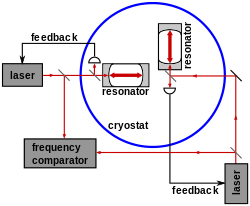
Michelson-Morley는 뮐러 등에 의해 사용된 것과 같은 형태의 극저온 광학 공진기로 실험했다.(2003), 최근의 광학 공진기 실험을 참조한다.
다음 항목도 참조하십시오.최근 Michelson-Morley 실험과 최근 Kennedy–가시 다이크 실험

Michelson-Morley와 Kennedy의 현대적 변종–빛 속도의 등방성을 테스트하기 위해 Thorndike 실험이 수행되었습니다.Michelson-Morley와 달리, Kennedy-Thorndike 실험은 다른 팔 길이를 사용하며, 평가는 몇 달 동안 지속된다.이러한 방식으로, 태양 주위를 도는 지구의 궤도 동안 다른 속도의 영향을 관찰할 수 있다.레이저, 메이저 및 광학 공진기를 사용하여 빛의 속도의 이방성을 10단계로−17 줄입니다.지상 테스트와 더불어 케네디-손다이크 [4]실험의 변형으로 달 레이저 거리 측정 실험도 실시되었습니다.

등방성 실험의 또 다른 유형은 1960년대 뫼스바우어 로터 실험으로, 뫼스바우어 효과를 사용하여 회전 디스크에 대한 도플러 효과의 이방성을 관찰할 수 있다(이러한 실험들은 시간 확장을 측정하기 위해 사용될 수도 있다, 아래 참조).

소스 속도 또는 에너지 의존 없음

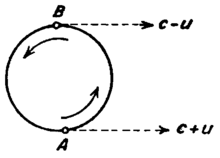
드 시터 이중성 실험은 나중에 Brecher에 의해 멸종 정리를 고려하여 반복되었다.

빛의 속도가 광원의 속도에 따라 달라지는 발광 이론은 에테르 표류 실험의 부정적인 결과를 설명할 수 있다.1960년대 중반이 되어서야 빛의 속도의 항상성이 확실하게 실험을 통해 증명되었습니다. 1965년, J. G. 폭스는 멸종 정리의 효과가 그 이전의 모든 실험의 결과를 결정적이지 않게 만들었고, 따라서 특수 상대성 이론과 방출 [9][10]이론 둘 다와 양립할 수 있다는 것을 보여주었습니다.최근의 실험은 확실히 방출 모델을 배제하고 있다. 가장 초기의 실험은 감마선의 이동원을 사용한 필리파스와 폭스([11]1964년)와 광자가 광원의 고속 붕괴 중간자의 속도를 얻지 못했다는 것을 증명한 알베거 외 연구진(1964년)[12]이다.또한, de Sitter 이중성 실험(1913년)은 소멸 정리를 고려하여 Brecher(1977년)에 의해 반복되었으며,[13] 소스 의존성도 배제되었다.

감마선 버스트 관측 결과 빛의 속도는 광선의 [14]주파수와 에너지와는 무관한 것으로 나타났다.

단방향 빛의 속도

주요 기사:단방향 빛의 속도

일련의 단방향 측정이 수행되었으며,[5] 모두 빛의 속도의 등방성을 확인하였다.단, 단방향 속도는 동시성의 정의와 그에 따라 동기화 방법에 따라 달라지기 때문에 쌍방향 빛의 속도(A에서 B로 다시 A로)만 명확하게 측정할 수 있다.아인슈타인 동기화 규칙은 단방향 속도를 양방향 속도와 동일하게 만듭니다.단, 등방성 쌍방향 빛의 속도를 가진 모델이 다수 있으며, 단방향 속도는 다른 동기 방식을 선택함으로써 이방성입니다.이것들은 실험적으로 특수 상대성 이론과 동등합니다. 왜냐하면 이 모든 모델들은 측정 가능한 이방성을 보상하는 움직이는 시계의 시간 확장과 같은 효과를 포함하기 때문입니다.그러나, 등방성 쌍방향 속도를 가진 모든 모델들 중에서, 오직 특수 상대성 이론만이 압도적으로 많은 물리학자들에게 받아들여질 수 있다. 왜냐하면 다른 모든 동기들은 훨씬 더 복잡하기 때문이다, 그리고 다른 모델들은 몇몇 동적 효과에 관한 극단적이고 믿을 수 없는 가정에 기초하고 있다.d 관찰로부터 "오브젝트 프레임"을 숨깁니다.

질량, 에너지 및 공간의 등방성

DO에서2 LiCl(1M)의 7Li-NMR 스펙트럼.리튬 동위원소의 선명하고 점멸되지 않은 NMR 라인은 질량과 공간의 등방성에 대한 증거이다.
다음 항목도 참조하십시오.휴즈-드레버 실험

휴즈-드레버 실험과 같은 클럭 비교 실험(주기적 프로세스와 주파수를 클럭으로 간주할 수 있음)은 로렌츠 불변성에 대한 엄격한 테스트를 제공합니다.그들은 Michelson-Morley로서 광자 부문에 제한되지 않고 원자핵의 지면 상태를 측정하여 질량, 에너지 또는 공간의 이방성을 직접 결정한다.이러한 이방성의 상한인 10−33 GeV가 제공되었다.따라서 이러한 실험은 지금까지 수행된 [3][4]로렌츠 불변성의 가장 정확한 검증 중 하나입니다.

시간 연장 및 길이 수축

Ives-Stilwell 실험(1938).
주요 기사:Ives – Stilwell 실험, 시간 연장 실험 및 길이 수축 확인

가로 도플러 효과와 그에 따른 시간 확장은 Ives-Stilwell 실험(1938년)에서 처음으로 직접 관찰되었다.포화 분광학을 사용한 중이온 저장 링에 대한 현대의 Ives-Stilwell 실험에서, 상대론적 예측으로부터 측정된 시간 확장의 최대 편차는 ≤ 10으로−8 제한되었다.시간 확장에 대한 다른 확인 사항으로는 회전 디스크의 중간에서 디스크의 가장자리에 있는 수신기로 감마선을 보내 뫼스바우어 효과를 뫼스바우어 효과로 평가할 수 있는 뫼스바우어 로터 실험이 있다.대기 중 뮤온과 입자 가속기에서 뮤온의 수명을 측정함으로써 움직이는 입자의 시간적 팽창도 검증했다.한편, Hafele-Keying 실험은 쌍둥이 역설의 분해능을 확인했습니다. 즉, A에서 B로 다시 이동하는 클럭은 초기 클럭에 대해 지연된다는 것입니다.그러나, 이 실험에서 일반 상대성 이론의 효과 또한 중요한 역할을 한다.

관찰된 입자의 치수가 매우 작기 때문에 실제로 길이 수축의 직접적인 확인은 어렵다.그러나 간접적인 확인도 있다. 예를 들어, 중이온과 충돌하는 행동은 로렌츠 수축에 의한 밀도가 증가된 것을 고려할 때에만 설명될 수 있다.수축은 또한 이미 효과가 관찰된 운동 방향에 수직인 쿨롱 장의 강도를 증가시킨다.따라서 입자 가속기에서 실험을 수행할 때는 시간 확장과 길이 축소를 모두 고려해야 한다.

상대론적 운동량과 에너지

속도 v/c의 함수로서 β 전자의 특정− 전하 e/m를 측정하기 위한 Bucherer의 실험 설정(자기장 H에 대한 각도α에서 베타 선원을 중심에 둔 원형 콘덴서의 축을 통한 단면적)
주요 기사:상대론적 에너지 및 운동량 테스트 및 카우프만-부체러-노이만 실험

1901년부터 전자 질량의 속도 의존성을 증명하기 위한 일련의 측정이 실시되었다.그 결과는 실제로 그러한 의존성을 보여주었지만, 경쟁 이론을 구별하는 데 필요한 정확성은 오랫동안 논란이 되었다.결국, 특수 상대성 이론을 제외한 모든 경쟁 모델들을 확실히 배제할 수 있었다.

오늘날 특수상대성이론의 예측은 상대론적 중이온 충돌기와 같은 입자 가속기에서 일상적으로 확인된다.예를 들어, 상대론적 운동량과 에너지의 증가는 정밀하게 측정될 뿐만 아니라 입자가 빛의 속도에 가깝게 가속되는 사이클로트론이나 싱크로트론 등의 거동을 이해하기 위해서도 필요하다.

사냐크와 피조

오리지널 Sagnac 간섭계
주요 기사: Sagnac 간섭계와 Fizau 실험

특수상대성이론은 또한 회전하는 폐쇄 경로(예: 루프)를 중심으로 반대 방향으로 이동하는 두 개의 광선이 이동 방출기/수신기로 돌아오기 위해서는 다른 비행 시간이 필요하다고 예측한다(이는 광속도가 선원의 속도로부터 독립한 결과이다, 위 참조).이 효과는 실제로 관찰되었으며 Sagnac 효과라고 불립니다.현재 이 효과에 대한 고려는 많은 실험 설정과 GPS의 올바른 기능을 위해 필요하다.

이러한 실험이 이동 매체(예: 물 또는 유리 광섬유)에서 수행되는 경우, Fizau 실험에서 입증되었듯이 프레넬의 드래그 계수를 고려할 필요가 있습니다.이 효과는 처음에는 거의 정지된 에테르 또는 부분 에테르 항력의 증거로 이해되었지만 속도 구성 법칙을 사용하여 특수 상대성 이론으로 쉽게 설명할 수 있다.

테스트 이론

주요 기사:특수상대성이론의 검정

표준 방정식에 특정 매개변수를 추가하여 로렌츠 위반 실험에서 가능한 양의 결과를 평가하기 위해 몇 가지 테스트 이론이 개발되었습니다.여기에는 RMS(Robertson-Mansouri-Sexl Framework)와 Standard-Model Extension(SME)이 포함됩니다.RMS에는 길이 수축 및 시간 연장에 관한 3가지 테스트 가능한 파라미터가 있습니다.이것에 의해, 빛의 속도의 이방성을 평가할 수 있다.한편 SME에는 특수상대성이론뿐만 아니라 표준모델과 일반상대성이론에도 로렌츠 위반 파라미터가 다수 포함되어 있어 테스트 가능한 파라미터의 수가 훨씬 많다.

기타 최신 테스트

주요 기사:로렌츠 위반에 대한 최신 검색

최근 몇 년 동안 양자 중력의 다양한 모델에 관한 발전으로 인해, 로렌츠 불변성의 편차(아마도 그러한 모델로부터 따라오는)가 다시 실험주의 표적이 되었다."LLI"(Local Lorentz 불변성)는 자유롭게 떨어지는 프레임에도 적용되기 때문에 약한 등가 원리에 관한 실험도 이 등급의 테스트에 속합니다.결과는 RMS와 같은 테스트 이론(상기) 또는 [3]SME에 의해 분석됩니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ a b c Laub, Jakob (1910). "Über die experimentellen Grundlagen des Relativitätsprinzips". Jahrbuch der Radioaktivität und Elektronik. 7: 405–463.
  2. ^ Zhang, Yuan Zhong (1997). Special Relativity and Its Experimental Foundations. World Scientific. ISBN 978-981-02-2749-4.
  3. ^ a b c Mattingly, David (2005). "Modern Tests of Lorentz Invariance". Living Rev. Relativ. 8 (5): 5. arXiv:gr-qc/0502097. Bibcode:2005LRR.....8....5M. doi:10.12942/lrr-2005-5. PMC 5253993. PMID 28163649.
  4. ^ a b c Will, C.M (2005). "Special Relativity: A Centenary Perspective". In T. Damour; O. Darrigol; B. Duplantier; V. Rivasseau (eds.). Poincare Seminar 2005. Basel: Birkhauser. pp. 33–58. arXiv:gr-qc/0504085. Bibcode:2006eins.book...33W. doi:10.1007/3-7643-7436-5_2. ISBN 978-3-7643-7435-8. S2CID 17329576.
  5. ^ a b Roberts, T; Schleif, S (2007). Dlugosz, JM (ed.). "What is the experimental basis of Special Relativity?". Usenet Physics FAQ. University of California, Riverside. Retrieved 2010-10-31.
  6. ^ Lodge, Oliver, Sir (1909). The Ether of Space. New York: Harper and Brothers.
  7. ^ Lämmerzahl, C. (2005). "Special Relativity and Lorentz Invariance". Annalen der Physik. 517 (1): 71–102. Bibcode:2005AnP...517...71L. doi:10.1002/andp.200410127.
  8. ^ a b Robertson, H. P. (1949). "Postulate versus Observation in the Special Theory of Relativity". Reviews of Modern Physics. 21 (3): 378–382. Bibcode:1949RvMP...21..378R. doi:10.1103/RevModPhys.21.378.
  9. ^ Fox, J. G. (1965), "Evidence Against Emission Theories", American Journal of Physics, 33 (1): 1–17, Bibcode:1965AmJPh..33....1F, doi:10.1119/1.1971219.
  10. ^ Martínez, Alberto A. (2004), "Ritz, Einstein, and the Emission Hypothesis", Physics in Perspective, 6 (1): 4–28, Bibcode:2004PhP.....6....4M, doi:10.1007/s00016-003-0195-6, S2CID 123043585
  11. ^ Filippas, T.A.; Fox, J.G. (1964). "Velocity of Gamma Rays from a Moving Source". Physical Review. 135 (4B): B1071-1075. Bibcode:1964PhRv..135.1071F. doi:10.1103/PhysRev.135.B1071.
  12. ^ Alväger, T.; Farley, F. J. M.; Kjellman, J.; Wallin, L. (1964), "Test of the second postulate of special relativity in the GeV region", Physics Letters, 12 (3): 260–262, Bibcode:1964PhL....12..260A, doi:10.1016/0031-9163(64)91095-9.
  13. ^ Brecher, K. (1977). "Is the speed of light independent of the velocity of the source". Physical Review Letters. 39 (17): 1051–1054. Bibcode:1977PhRvL..39.1051B. doi:10.1103/PhysRevLett.39.1051.
  14. ^ Fermi LAT Collaboration (2009). "A limit on the variation of the speed of light arising from quantum gravity effects". Nature. 462 (7271): 331–334. arXiv:0908.1832. Bibcode:2009Natur.462..331A. doi:10.1038/nature08574. PMID 19865083. S2CID 205218977.