도플러 효과
Doppler effect
도플러 효과 또는 도플러 시프트(또는 [1][2]단순히 상황에 맞는 도플러)는 파동 소스에 대해 움직이는 [3]관찰자에 대한 파동의 주파수 변화입니다.그것은 1842년에 이 현상을 묘사한 오스트리아의 물리학자 크리스티안 도플러의 이름을 따서 붙여졌다.
도플러 시프트의 일반적인 예는 경적을 울리는 차량이 관찰자로부터 접근하거나 후퇴할 때 들리는 음조의 변화입니다.방출 주파수에 비해 수신 주파수는 접근 중에 높고, 통과하는 순간에는 동일하며,[4] 불황기에는 낮다.
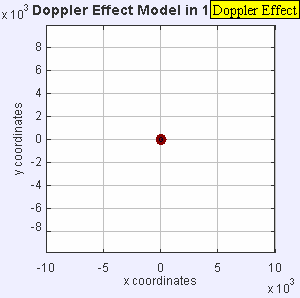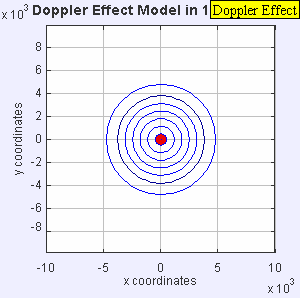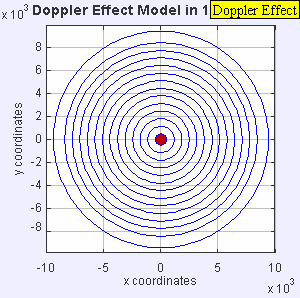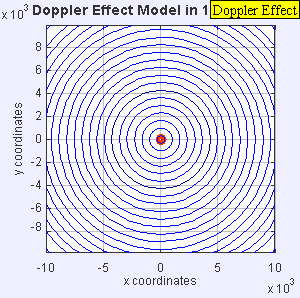
도플러 효과의 이유는 파장의 근원이 관찰자를 향해 움직일 때 각각의 연속된 파동의 정점이 이전 [4][5]파동의 정점보다 관찰자에 더 가까운 위치에서 방출되기 때문입니다.따라서 각 파형이 이전의 파동보다 관찰자에게 도달하는 데 걸리는 시간이 약간 줄어듭니다.따라서 관측자에 연속되는 파형의 도달간 시간이 단축되어 주파수의 증가를 일으킨다.이동하는 동안 연속된 파동 전선 사이의 거리가 줄어들기 때문에 파동이 "뭉쳐"집니다.반대로 파원이 옵저버에서 멀어질 경우 각 파장은 전파보다 옵저버에서 멀리 떨어진 위치에서 방출되므로 연속파 간의 도달시간이 증가하여 주파수가 감소한다.연속된 파동 전선 사이의 거리가 증가하므로 파동이 "확대"됩니다.
음파와 같은 매체에서 전파되는 파동의 경우 관측자 및 선원의 속도는 [3]파동이 전달되는 매체에 상대적입니다.따라서 총 도플러 효과는 소스의 움직임, 관찰자의 움직임 또는 매체의 움직임에서 발생할 수 있습니다.이러한 효과는 각각 개별적으로 분석됩니다.전자파나 중력파처럼 매체가 필요 없는 파장은 관측자와 선원의 상대적인 속도 차이만 고려하면 된다.이 상대속도가 빛의 속도에 비해 무시할 수 없는 정도가 아닐 때, 더 복잡한 상대론적 도플러 효과가 발생한다.
역사
도플러는 1842년 그의 논문 "Uber das farbige Licht der Doupelsterne und Einigererer Gestirne des Himmels"[6]에서 이 효과를 처음 제안했다.이 가설은 1845년 [p 1]Buys Ballout에 의해 음파에 대한 시험을 거쳤다.그는 음원이 자신에게 다가왔을 때 음높이가 방출 주파수보다 높고 음원이 자신에게서 멀어질 때 방출 주파수보다 낮다는 것을 확인했다.히폴리테 피조는 1848년 전자파에서 같은 현상을 독립적으로 발견했다(프랑스에서는 "에페트 도플러-피조"라고 부르기도 하지만, 피조의 발견은 도플러의 [p 2][7]제안 이후 6년 후였기 때문에 다른 나라들에 의해 받아들여지지 않았다).영국에서, 존 스콧 러셀은 도플러 효과에 대한 실험적인 연구를 했다.[p 3]
일반
매체에 대한 소스 및 수신기의 속도가 매체의 파동 속도보다 낮은 고전 물리학에서 관측 f {\방출 주파수 f 0 {\text{ 사이의 관계는 다음과 같이 [8]구한다.
- c는 매질 내 파동의 전파 속도이다.
- r{\는 수신기가 소스 쪽으로 이동하는 경우 c{\ c에 더하고 수신기가 소스로부터 멀어지는 경우 빼는 입니다.
- s {\s}}}는 미디어에 대한 소스의 상대적인 속도입니다.소스가 수신기에서 멀어지는 경우c {\ c에 가산됩니다.소스가 수신기로 이동하고 있는 경우 감산됩니다.
이 관계에서는, 송신원 또는 수신기의 어느쪽이 다른 쪽으로부터 멀어질 경우, 주파수가 감소한다고 예측하고 있습니다.
마찬가지로, 선원이 관찰자에게 직접 접근하거나 관찰자에게서 멀어지고 있다는 가정 하에:
- w \ 은 수신기에 상대적인 파동 속도이다.
- s\ 는 선원에 대한 파동의 속도이다.
- \da는 입니다.
음원이 일정한 각도로 관찰자에게 접근하면(그러나 여전히 일정한 속도로), 처음 들리는 관측 주파수는 물체의 방출 주파수보다 높아집니다.그 후, 상대 운동과 수직인 방향에서 (그리고 가장 가까운 접근 지점에서 방출되었지만, 파동이 수신될 때, 선원과 관측자는 더 이상 가장 가까운 위치에 있지 않을 때) 등식을 통해 관측된 주파수의 단조로운 감소가 관찰자에 가까워질수록 계속된다.관찰자로부터 멀어질수록 단조가 감소합니다.관찰자가 물체의 경로에 매우 가까이 있으면 고주파에서 저주파로의 전환이 매우 갑작스럽게 이루어집니다.관찰자가 물체의 경로에서 멀리 떨어져 있을 때, 고주파에서 저주파로의 전환은 점진적으로 이루어집니다.
속도 s{\ r {\이 파동 속도에 비해 작을 경우 주파수 {\f}와 f0}} 사이의 관계는 약하다[8].
| 관측 주파수 | 빈도의 변화 |
|---|---|
어디에
- v -( r- s \ v=-(s}}}}}}는 소스와 리시버가 서로 향하고 있을 때 양의 속도이다.
( c+ c + ) 0{ f = \ + v _ { \ { } } { + v { \ { } } \ ) }
c{ c}에 분할합니다.
c1 1)이므로 기하학적 확장을 대체할 수 있습니다.
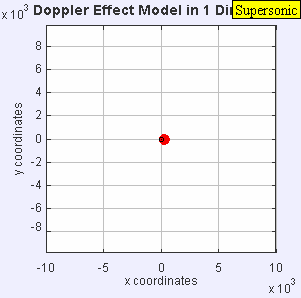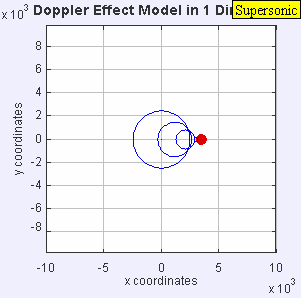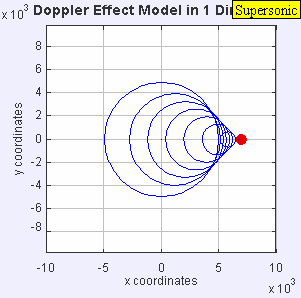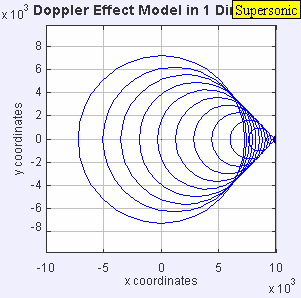
같은 음원이 같은 매체에 일정한 주파수로 음파를 방사하는 것입니다.그러나 이제 음원은 θs = 0.7 c의 속도로 이동한다. 음원은 이동 중이기 때문에 각 새로운 파면의 중심은 오른쪽으로 약간 이동한다.그 결과, 웨이브 프론트는 오른쪽(전방)에서 뭉치기 시작해, 소스의 왼쪽(후방)에서 더 멀리 퍼집니다.소스의 앞에 있는 관찰자. 더 높은 주파수 f).mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1을 들을 것입니다.엠}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}c+0/c – 0.7c f0)을 가졌고 3.33f0 원본 뒤의 한 관찰자 c− 0/c+0.7c f0)더 낮은 주파수 f)을 들을 수가 0.59f0.
결과들
매체에 대해 관측자가 정지해 있을 때 이동원이 f0는 일정하게 유지되며 전파속도는 전파원의 속도에 좌우되지 않음)의 파장을 방출하는 경우 t옵서버는 f f의 를 사용하여 파동을 검출합니다.
이동 중인 관찰자와 정지 선원에 대한 유사한 분석(이 경우 파장은 일정하게 유지되지만 운동으로 인해 관찰자가 파장을 수신하는 속도와 (관찰자에 대한) 파동의 전송 속도가 변경됨)은 관측 주파수를 산출합니다.
정지 상태의 관찰자와 음속으로 이동하는 소스를 가정하면, 도플러 방정식은 음속으로 이동하는 소스 앞에서 관찰자에 의해 지각된 순간적인 무한 주파수를 예측한다.모든 피크가 같은 장소에 있기 때문에 파장은 0이고 주파수는 무한합니다.이 모든 파장의 오버레이는 음파의 경우 소닉 붐이라고 하는 충격파를 생성합니다.
소스가 파속보다 빠르게 이동하면 소스가 파동을 앞지릅니다.이 방정식은 음의 주파수 값을 제공하는데, 이는 이러한 맥락에서 물리적 감각이 없습니다(소스가 음수를 통과할 때까지 관찰자가 소리를 전혀 듣지 않습니다).
레일리 경은 소리에 관한 그의 고전에서 다음과 같은 효과를 예측했다: 만약 관찰자가 음속의 두 배 속도로 (정지된) 음원에서 움직인다면, 그 음원에서 이전에 방출된 음악 작품은 정확한 템포와 음조로 들릴 것이지만,[9] 마치 거꾸로 연주되는 것처럼 들릴 것이다.
적용들
음향 도플러 전류 프로파일러
음향 도플러 전류 프로파일러(ADCP)는 수중 음파탐지기와 유사한 수중 전류계이며, 물기둥 내의 입자에서 산란된 음파의 도플러 효과를 사용하여 깊이 범위의 물 전류 속도를 측정하는 데 사용됩니다.ADCP라는 용어는 모든 음향 전류 프로파일러의 총칭이지만, 약어는 1980년대에 RD Instruments에서 도입한 계측기 시리즈에서 유래했습니다.ADCP의 작동 주파수 범위는 38kHz에서 수 MHz까지입니다.소리를 이용한 풍속 프로파일링을 위해 공기 중에 사용되는 장치는 SODAR로 알려져 있으며 동일한 기본 원리로 작동합니다.
로보틱스
움직이는 장애물이 있는 정교한 환경에서 로봇의 이동을 돕는 로봇 공학에서의 동적 실시간 경로 계획은 종종 도플러 효과를 [10]돕는다.이러한 애플리케이션은 로보 축구와 같이 환경이 끊임없이 변화하는 경쟁 로봇 공학에 특히 사용됩니다.
사이렌
지나가는 응급 차량의 사이렌은 정지 피치보다 높게 출발하여 통과할 때 아래로 미끄러져 내려가고 관찰자로부터 물러날 때 정지 피치보다 낮게 계속 울립니다.천문학자 존 돕슨은 그 효과를 다음과 같이 설명했다.
사이렌이 미끄러지는 이유는 부딪히지 않기 때문입니다.
즉, 사이렌이 관찰자에게 직접 접근하면, 차가 그를 칠 때까지 피치는 정지된 피치보다 높은 피치로 일정하게 유지되고, 그 후 즉시 새로운 저피치로 점프한다.차량이 관찰자를 통과하기 때문에 반경 속도는 일정하게 유지되지 않고, 대신 시야와 사이렌 속도 사이의 각도에 따라 변화합니다.
천문학
빛과 같은 전자파에 대한 도플러 효과는 별과 은하가 우리에게 접근하거나 멀어지는 속도를 측정하기 위해 천문학에서 널리 사용되며, 각각 블루시프트 또는 레드시프트라고 불립니다.이것은 실제로 하나의 별이 가까운 쌍성인지, 별과 은하의 회전 속도를 측정하기 위해 또는 외부 행성을 탐지하는 데 사용될 수 있습니다.이 효과는 일반적으로 매우 작은 규모로 발생하며, 육안으로 [11]볼 수 있는 가시광선에는 현저한 차이가 없을 것이다.천문학에서 도플러 효과의 사용은 별의 스펙트럼에서 이산적인 선의 정확한 주파수에 대한 지식에 달려 있다.
가까운 별들 중 태양에 대한 가장 큰 반지름 속도는 +308 km/s(LHS 52로 알려진 BD-15°4041)와 -260 km/s(울프 9722로 알려진 울프 1106 및 LHS 64로 알려진 78.2 광년)이다.반지름 속도가 양수라는 것은 별이 태양으로부터 멀어지고 있다는 것을 의미하며, 음수라는 것은 가까이 오고 있다는 것을 의미합니다.
적색 편이 또한 공간의 팽창을 측정하는 데 사용되지만, 이것은 사실 도플러 [12]효과가 아니다.오히려, 공간의 팽창으로 인한 적색 이동은 우주론적 적색 이동으로 알려져 있는데, 이것은 일반 상대성 이론의 형식주의 하에서 순수하게 로버트슨-워커 측정법에서 파생될 수 있다.이렇게 말했지만, 우주론적 척도에 감지 가능한 도플러 효과가 있다는 사실도 발생하는데, 이것이 우주론적 기원으로 잘못 해석되면 적색 편이-공간 [13]왜곡을 관찰하게 된다.
레이더

도플러 효과는 감지된 물체의 속도를 측정하기 위해 일부 유형의 레이더에서 사용됩니다.레이더 빔은 레이더 소스에 접근하거나 레이더 소스에서 멀어질 때 경찰이 레이더를 사용하여 과속 운전자를 탐지할 때 움직이는 표적(예: 자동차)을 향해 발사된다.각각의 연속된 레이더 파동은 반사되어 근원 근처에서 재검출되기 전에 자동차에 도달하기 위해 더 멀리 이동해야 합니다.각 파형이 더 멀리 이동해야 할 때, 각 파동 사이의 간격이 커져 파장이 커집니다.어떤 상황에서는 레이더 빔이 움직이는 차에 접근하면서 발사되는데, 이 경우 각각의 연속된 파장은 더 적은 거리를 이동하며 파장을 감소시킵니다.어느 경우든 도플러 효과의 계산에 의해 차의 속도가 정확하게 결정됩니다.게다가, 제2차 세계대전 중에 개발된 근접 퓨즈는 정확한 시간, 높이,[citation needed] 거리 등에서 폭발물을 터뜨리기 위해 도플러 레이더를 이용한다.
도플러 시프트는 레이더로 반사되는 파동뿐만 아니라 대상에 입사하는 파동에 영향을 미치기 때문에, 상대 속도 v \v로 인해 레이더에 의해 관측되는 주파수의 변화는 [14]파동을 방출하는 동일한 표적의 두 배입니다.
의료의

심장 초음파 검사는 도플러 효과를 사용하여 임의의 지점에서 혈류 방향과 혈액 및 심장 조직의 속도를 일정 한도 내에서 정확하게 평가할 수 있습니다.한계 중 하나는 초음파 빔이 가능한 한 혈류와 평행해야 한다는 것입니다.속도 측정을 통해 심장 판막 영역 및 기능 평가, 심장의 왼쪽과 오른쪽 사이의 비정상적인 통신, 밸브를 통한 혈액 누출(판막 역류) 및 심박출량 계산을 수행할 수 있습니다.가스 충전 마이크로버블 조영제를 사용한 조영 증강 초음파는 속도 또는 기타 흐름 관련 의학적 [15][16]측정을 개선하기 위해 사용될 수 있다.
"도플러"는 의료 영상에서 "속도 측정"과 동의어가 되었지만, 대부분의 경우 측정되는 것은 수신 신호의 주파수 이동(도플러 이동)이 아니라 위상 이동(수신 신호가 [p 4]도착할 때)입니다.
혈류 속도 측정은 산부인과 초음파 및 신경학 등 의료 초음파 검사 분야에서도 사용됩니다.도플러 효과에 기초한 동맥과 정맥의 혈류 속도 측정은 협착과 [17]같은 혈관 문제를 진단하는 데 효과적인 도구입니다.
흐름 측정
유체 흐름의 속도를 측정하기 위해 레이저 도플러 속도계(LDV)와 음향 도플러 속도계(ADV)와 같은 기구들이 개발되었다.LDV는 광빔을 방출하고 ADV는 초음파 음향 버스트를 방출하며 흐름과 함께 움직이는 입자의 반사 파장의 도플러 편이를 측정합니다.실제 흐름은 수속과 위상의 함수로 계산된다.이 기술을 사용하면 고정밀 및 고주파수로 비침입 유량을 측정할 수 있습니다.
속도 프로필 측정
원래는 의료 애플리케이션(혈류)의 속도 측정을 위해 개발된 초음파 도플러 속도계(UDV)는 먼지, 가스 거품, 유화 등 부유 입자를 포함한 거의 모든 액체에서 실시간으로 완전한 속도 프로파일을 측정할 수 있습니다.흐름은 맥동, 진동, 층류 또는 난류, 정지 또는 과도입니다.이 기술은 완전히 비침습적입니다.
위성
도플러 시프트는 트랜짓 및 DORIS와 같은 위성 항법에 이용될 수 있습니다.
위성 통신
도플러도 위성통신에 대한 보상이 필요하다.빠르게 움직이는 위성은 지상국에 대해 수십 킬로헤르츠의 도플러 시프트를 가질 수 있다.속도, 즉 도플러 효과의 크기는 지구의 곡률에 의해 변화합니다.송신중에 신호의 주파수가 단계적으로 변화하는 동적 도플러 보상을 이용해, 위성이 일정한 주파수 [19]신호를 수신한다.2005년 카시니호의 호이겐스 탐사선이 발사되기 전에는 도플러 이동이 고려되지 않았다는 것을 깨달은 후-Huygens 미션, 탐사선의 궤도는 타이탄에 접근하도록 바뀌었습니다. 전송이 카시니에 상대적인 운동 방향과 직각을 이루도록 하여, 도플러 이동을 [20]크게 줄였습니다.
직접 경로의 도플러 이동은 다음 [21]공식으로 추정할 수 있습니다.
위성 이동으로 인한 추가 도플러 이동은 다음과 같이 설명할 수 있습니다.
오디오
유명한 해먼드 오르간과 가장 많이 관련되고 주로 사용되는 레슬리 스피커는 전기 모터를 사용하여 스피커 주위의 음향 경적을 회전시켜 소리를 원형으로 전달함으로써 도플러 효과를 활용합니다.이로 인해 청취자의 귀에 키보드 노트의 주파수가 빠르게 변동합니다.
진동 측정
레이저 도플러 진동계(LDV)는 진동을 측정하기 위한 비접촉 기기입니다.LDV에서 나오는 레이저 빔은 해당 표면을 향해 있으며, 표면의 움직임에 따라 레이저 빔 주파수의 도플러 시프트에서 진동 진폭과 주파수를 추출합니다.
발달생물학
척추동물의 배아가 분할되는 동안 유전자 발현 파동은 척추(소마이트)의 전구체가 형성되는 조직인 전엽 중엽을 휩쓸고 지나간다.전암 중배엽의 전단에 파동이 도달하면 새로운 소마이트가 형성된다.제브라피쉬에서는 분할 중 전암 중배엽의 단축이 조직의 앞끝이 파도로 이동함에 따라 도플러와 같은 효과를 가져오는 것으로 나타났다.이 효과는 [p 5]분할 기간에 기여합니다.
역도플러 효과
1968년부터 빅터 베셀라고와 같은 과학자들은 역도플러 효과의 가능성에 대해 추측해 왔다.도플러 이동의 크기는 파동이 통과하는 매체의 굴절률에 따라 달라집니다.하지만 어떤 물질들은 음의 굴절이 가능하기 때문에 기존의 도플러 [22]이동과는 반대 방향으로 도플러 이동이 일어날 것이다.이 효과를 발견한 첫 번째 실험은 2003년 [p 6]영국 브리스톨에서 나이젤 세든과 트레버 베어파크에 의해 이루어졌다.이후 일부 비균질 물질에서 역도플러 효과가 관측되었고 Vavilov-Cherenkov [23]원뿔 내부에서 예측되었다.
「 」를 참조해 주세요.
주요 소스
- ^ Buys Ballot (1845). "Akustische Versuche auf der Niederländischen Eisenbahn, nebst gelegentlichen Bemerkungen zur Theorie des Hrn. Prof. Doppler (in German)". Annalen der Physik und Chemie. 142 (11): 321–351. Bibcode:1845AnP...142..321B. doi:10.1002/andp.18451421102.
- ^ 피조: "Acoustique et optique"Societe Philomathique de Paris, 1848년 12월 29일 강연.베커에 따르면, 이것은 결코 출판되지 않았고, M에 의해 언급되었다.Moigno(1850): "Répertoire d'optique moderne"(프랑스어), vol. pp 1165–1203 그리고 나중에 Fizeau에 의해 완전히 "Des effets duvement sur le ton des vibrations sonores et la longur d'onde d'l d'rayon de lumier; (파리, 1870)".아날레스 드 치미에 외 체격, 19, 211–221.
- ^ Scott Russell, John (1848). "On certain effects produced on sound by the rapid motion of the observer". Report of the Eighteenth Meeting of the British Association for the Advancement of Science. 18 (7): 37–38. Retrieved 2008-07-08.
- ^ Petrescu, Florian Ion T (2015). "Improving Medical Imaging and Blood Flow Measurement by using a New Doppler Effect Relationship". American Journal of Engineering and Applied Sciences. 8 (4): 582–588. doi:10.3844/ajeassp.2015.582.588 – via Proquest.
- ^ Soroldoni, D.; Jörg, D. J.; Morelli, L. G.; Richmond, D. L.; Schindelin, J.; Jülicher, F.; Oates, A. C. (2014). "A Doppler Effect in Embryonic Pattern Formation". Science. 345 (6193): 222–225. Bibcode:2014Sci...345..222S. doi:10.1126/science.1253089. PMC 7611034. PMID 25013078. S2CID 206556621.
- ^ Kozyrev, Alexander B.; van der Weide, Daniel W. (2005). "Explanation of the Inverse Doppler Effect Observed in Nonlinear Transmission Lines". Physical Review Letters. 94 (20): 203902. Bibcode:2005PhRvL..94t3902K. doi:10.1103/PhysRevLett.94.203902. PMID 16090248.
레퍼런스
- ^ United States. Navy Department (1969). Principles and Applications of Underwater Sound, Originally Issued as Summary Technical Report of Division 6, NDRC, Vol. 7, 1946, Reprinted...1968. p. 194. Retrieved 2021-03-29.
- ^ Joseph, A. (2013). Measuring Ocean Currents: Tools, Technologies, and Data. Elsevier Science. p. 164. ISBN 978-0-12-391428-6. Retrieved 2021-03-30.
- ^ a b Giordano, Nicholas (2009). College Physics: Reasoning and Relationships. Cengage Learning. pp. 421–424. ISBN 978-0534424718.
- ^ a b Possel, Markus (2017). "Waves, motion and frequency: the Doppler effect". Einstein Online, Vol. 5. Max Planck Institute for Gravitational Physics, Potsdam, Germany. Archived from the original on September 14, 2017. Retrieved September 4, 2017.
- ^ Henderson, Tom (2017). "The Doppler Effect – Lesson 3, Waves". Physics tutorial. The Physics Classroom. Retrieved September 4, 2017.
- ^ 알렉 에덴 1992년 빈, 스프링거-벨라그, 크리스찬 도플러를 찾습니다.영어 번역 팩시밀리 에디션이 포함되어 있습니다.
- ^ Becker(2011).Barbara J. Becker, Unlavelling Starlight: William and Margaret Huggins and the Rise of the New Astronomy, 일러스트 에디션, 캠브리지 대학 출판부, 2011; ISBN 110700229X, 978107002296.
- ^ a b Rosen, Joe; Gothard, Lisa Quinn (2009). Encyclopedia of Physical Science. Infobase Publishing. p. 155. ISBN 978-0-8160-7011-4.
- ^ Strutt (Lord Rayleigh), John William (1896). MacMillan & Co (ed.). The Theory of Sound. Vol. 2 (2 ed.). Macmillan. p. 154.
- ^ Agarwal, Saurabh; Gaurav, Ashish Kumar; Nirala, Mehul Kumar; Sinha, Sayan (2018). "Potential and Sampling Based RRT Star for Real-Time Dynamic Motion Planning Accounting for Momentum in Cost Function". Neural Information Processing. Lecture Notes in Computer Science. Vol. 11307. pp. 209–221. doi:10.1007/978-3-030-04239-4_19. ISBN 978-3-030-04238-7.
- ^ "Doppler Shift". astro.ucla.edu.
- ^ 그 구별은 에서 명백하다.
- ^ 이 토픽에 대한 기술적인 세부사항의 훌륭한 리뷰는 다음과 같습니다.
- ^ Wolff, Dipl.-Ing. (FH) Christian. "Radar Basics". radartutorial.eu. Retrieved 14 April 2018.
- ^ Davies, MJ; Newton, JD (2 July 2017). "Non-invasive imaging in cardiology for the generalist". British Journal of Hospital Medicine. 78 (7): 392–398. doi:10.12968/hmed.2017.78.7.392. PMID 28692375.
- ^ Appis, AW; Tracy, MJ; Feinstein, SB (1 June 2015). "Update on the safety and efficacy of commercial ultrasound contrast agents in cardiac applications". Echo Research and Practice. 2 (2): R55–62. doi:10.1530/ERP-15-0018. PMC 4676450. PMID 26693339.
- ^ Evans, D. H.; McDicken, W. N. (2000). Doppler Ultrasound (2nd ed.). New York: John Wiley and Sons. ISBN 978-0-471-97001-9.[페이지 필요]
- ^ 오틸리아 포페스키, 제이슨 S.Harrisz와 Dimitrie C.Popescuz, Nanosatellite CubeSat 미션용 통신 서브시스템 설계: 운영 및 구현 관점, 2016, IEEE
- ^ Qingchong, Liu (1999), "Doppler measurement and compensation in mobile satellite communications systems", Military Communications Conference Proceedings / MILCOM, 1: 316–320, CiteSeerX 10.1.1.674.3987, doi:10.1109/milcom.1999.822695, ISBN 978-0-7803-5538-5, S2CID 12586746
- ^ Oberg, James (October 4, 2004). "Titan Calling How a Swedish engineer saved a once-in-a-lifetime mission to Saturn's mysterious moon". IEEE Spectrum. (2006-10-14 현재 오프라인, "인터넷 아카이브 버전" 참조)
- ^ Arndt, D. (2015년)육상 이동 위성 수신을 위한 채널 모델링(박사 논문)
- ^ "Doppler shift is seen in reverse". Physics World. 10 March 2011.
- ^ Shi, Xihang; Lin, Xiao; Kaminer, Ido; Gao, Fei; Yang, Zhaoju; Joannopoulos, John D.; Soljačić, Marin; Zhang, Baile (October 2018). "Superlight inverse Doppler effect". Nature Physics. 14 (10): 1001–1005. arXiv:1805.12427. Bibcode:2018arXiv180512427S. doi:10.1038/s41567-018-0209-6. ISSN 1745-2473. S2CID 125790662.
추가 정보
- 도플러, C. (1842)Uber das farbige Licht der Doupelsterne und Einiger와 Gestirne des Himmels(쌍성 및 하늘의 다른 별들의 색채 빛에 대하여)출판사: Abhandlungen der Königl.Böhm. Gesellschaft der Wissenschaften (V. Folge, Bd. 2, S.465–482) [왕립 보헤미안 과학회 (V. Part, Vol.)]; 프라하: 1842 (1903년 재발행).일부 출처는 1843년을 출판 연도로 언급하고 있는데, 그 해에 그 기사가 보헤미안 과학 협회의 회보에 게재되었기 때문이다.도플러는 1842년 그가 독립적으로 배포한 예비판을 인쇄했기 때문에 그 출판물을 "Prag 1842 bei Borrosch and Andre"라고 불렀다.
- "도플러와 도플러 효과", E. N. da C.Andrade, Endever Vol. XVIII 제69호, 1959년 1월(ICI 런던 출판)도플러의 원본 논문과 그 이후의 전개에 대한 역사적 설명.
- David Nolte (2020).도플러 효과의 하락과 상승.오늘 물리 v. 73, pgs. 31 - 35.DOI: 10.1063 / PT.3.4429
- Adrian, Eleni (24 June 1995). "Doppler Effect". NCSA. Archived from the original on 12 May 2009. Retrieved 2008-07-13.







 수신기가 소스 쪽으로 이동하는 경우 c
수신기가 소스 쪽으로 이동하는 경우 c 미디어에 대한 소스의 상대적인 속도입니다.소스가 수신기에서 멀어지는 경우
미디어에 대한 소스의 상대적인 속도입니다.소스가 수신기에서 멀어지는 경우

 선원에 대한 파동의 속도이다.
선원에 대한 파동의 속도이다.






 기하학적 확장을 대체할 수 있습니다.
기하학적 확장을 대체할 수 있습니다.






 물체의 전진 속도와 물체에서 관찰자까지의 시선 사이의 각도입니다.
물체의 전진 속도와 물체에서 관찰자까지의 시선 사이의 각도입니다. 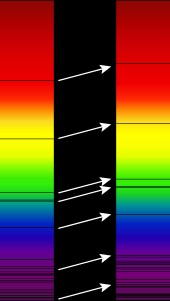




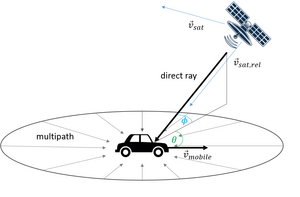

 이동국의 속도,
이동국의 속도,  위성의 상대 속도,
위성의 상대 속도,  위성의 고도 각도입니다.
위성의 고도 각도입니다.

 위성 이동에 따른 추가 도플러 시프트입니다.
위성 이동에 따른 추가 도플러 시프트입니다.
 반송파의 파장,
반송파의 파장, 
 위성의 상대 속도입니다.
위성의 상대 속도입니다. 

