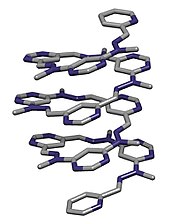
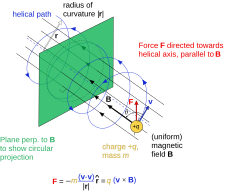
선 주위에 감기는 공간 곡선
t = 0 ~ 4cm의 오른쪽 나선(cos t, sin t , t)과 t 증가 방향을 나타내는 화살표 나선형(/ks/)은 코르크 마개 또는 나선형 계단 같은 형태입니다. 이것은 고정된 축에 대해 일정 한 각도로 접선이 있는 매끄러운 공간 곡선 의 한 유형입니다. DNA 분자가 두 개 의 얽힌 나선형 으로 형성되고 많은 단백질이 알파 나선형 으로 알려진 나선형 하부 구조를 가지고 있기 때문에 나선형은 생물학에서 중요 하다.헬릭스라는 단어 는 그리스어 ἕιξ ,, " " " " "에서 유래했다.[1] "충전된" 나선형(예: "나선형" 램프)은 [2] 불리는
속성 및 유형 나선 나선 의 회전 높이이다.
이중 나선은 같은 축을 가진 두 개의 나선형(일반적 으로 합치)으로 구성되며 [3]
원형나선 (즉 반지름이 일정한 것)은 일정 한 밴드 곡률 및 일정 한 비틀림을 가진다.
원뿔 나선이라고도 알려진 원뿔 나선은 원뿔 표면상 의 나선형으로 정의될 수 있으며, 원뿔 표면에서의 거리는 축으로부터의 방향을 나타내는 각도의 지수 함수이다.
곡선은 탄젠트가 공간에서 일정한 선과 일정한 각도를 이루는 경우 일반나선 또는 원통나선 이라고[4] 곡선은 곡률 대 비틀림 비율 이 [5]
곡선의 주 법선이 [6] 경사나선 이라고 불립니다. 일반 [7]
보다 일반적인 나선형 공간 곡선은 공간 나선형(예: 구형 나선형)을 참조 할 수 있다.
손재주 나선형은 오른손잡이 또는 왼손잡이일 수 있습니다. 나선의 축을 따라 조준선이 있을 때 시계방향으로 나사를 돌려서 나선을 관찰자로부터 멀어지게 하면 오른손나선이라고 하고 관찰자 쪽으로 가면 왼손나선이라고 합니다. 핸드니스(또는 키랄리티)는 원근법이 아닌 나선의 특성입니다.오른손 나선은 거울에 비치지 않는 한 왼손 나선으로 변할 수 없으며, 그 반대도 마찬가지입니다.
두 가지 유형의 나선이 비교 에 제시되어 있습니다.이것은 나선형의 두 가지 카이랄성을 보여준다. 하나는 왼손잡이고 다른 하나는 오른손잡이다. 각 행은 서로 다른 관점에서 두 개의 나선형을 비교합니다. 키랄리티는 원근법 (뷰 각도)이 아닌 객체의 속성입니다. 수학적 설명 수학 에서, 나선은 3차원 공간에서의 곡선 이다.데카르트 좌표 의 다음 매개변수 는 특정한 [8]
x ( t ) = 왜냐하면 ( t ) , {\displaystyle x(t)=\cos(t),,} y ( t ) = 죄 ( t ) , {\displaystyle y(t)=\sin(t),,} z ( t ) = t . {\displaystyle z(t)=t.,} 파라미터 t가 증가함에 따라 점(x (t ),y (t ),z (t ))는 오른손 좌표계에서 z축을 중심으로 피치 2µ(또는 경사 1) 및 반지름 1의 오른손 나선을 추적한다.
원통 좌표 (r , θ , h )에서 동일한 나선은 다음과 같이 매개변수를 구한다.
r ( t ) = 1 , {\displaystyle r(t)=1,,} θ ( t ) = t , {\displaystyle \theta(t)=t,,} h ( t ) = t . {\displaystyle h(t)=t.,} 반지름 a와 경사 a/b (또는 피치 2µb )의 원형 나선은 다음과 같은 매개 변수로 설명된다.
x ( t ) = a 왜냐하면 ( t ) , {\displaystyle x(t)=a\cos(t),,} y ( t ) = a 죄 ( t ) , {\displaystyle y(t)=a\sin(t),,} z ( t ) = b t . {\displaystyle z(t)=bt.,} 나선을 수학적으로 구성하는 또 다른 방법은 복소수 함수xi e를 실수 x의 함수로 표시하는 것이다(오일러 공식 참조 ). x의 값 과 함수 값의 실수 및 허수 부분은 이 그림에 3차원을 제공합니다.
회전 , 변환 및 스케일 변경을 제외하고 모든 오른손 나선은 위에서 정의한 나선과 동일합니다.등가 왼손 나선은 여러 가지 방법으로 구성될 수 있으며, 가장 간단한 방법 은 x , y 또는 z 성분 중 하나를 부정하는 것이다.
호 길이, 곡률 및 비틀림 반지름 a와 경사 a/b (또는 피치 2µb )의 원형 나선의 호 길이는 다음 과 같이 직사각형 좌표로 표현된다.
t ↦ ( a 왜냐하면 t , a 죄 t , b t ) , t ∈ [ 0 , T ] {\displaystyle t\mapsto(a\cos t,a\sin t,bt),t\in [0,T]} T † a b 2 displaystyle cdot sqrt a ^ b^ 2 }}}}}, 곡률 a 2 2(\displaystyle } {a^{2 2 . }}}}} 비틀림 b a 2 b 2. {{displaystyle a^{2}+b^{
나선은 벡터 값 함수입니다.
r = a 왜냐하면 t i + a 죄 t j + b t k \displaystyle \mathbf {r} =a\cos t\mathbf {i} +a\sin t\mathbf {j} +bt\mathbf {k}
v = − a 죄 t i + a 왜냐하면 t j + b k \displaystyle \mathbf {v} =-a\sin t\mathbf {i} +a\cos t\mathbf {j} +b\mathbf {k}
a = − a 왜냐하면 t i − a 죄 t j + 0 k \displaystyle \mathbf {a} =-a\cos t\mathbf {i} -a\sin t\mathbf {j} +0\mathbf {k}
v = ( − a 죄 t ) 2 + ( a 왜냐하면 t ) 2 + b 2 = a 2 + b 2 {\displaystyle \mathbf {v} = paramrt {(-a\sin t)^{2}+(a\cos t)^{2}+b^{2 }} = paramrt {a^{2}+b^{2} }}}}
a = ( − a 죄 t ) 2 + ( a 왜냐하면 t ) 2 = a {\displaystyle \mathbf {a} = paramrt {(-a\sin t)^{2}+(a\cos t)^{2}} = a}
s ( t ) = ∫ 0 t a 2 + b 2 d τ = a 2 + b 2 t {\displaystyle s(t)=\int _{0}^{t}{\displayrt {a^2}+b^{2} }}d\contract = scont {a^{2}+b^{2} }}}}t}
따라서 displaystyle s
r ( s ) = a 왜냐하면 s a 2 + b 2 i + a 죄 s a 2 + b 2 j + b s a 2 + b 2 k {\displaystyle \mathbf {r} (s)=a\cos {frac {s}{\cosrt {a^{2}+b^{2} }}}}:\mathbf {i} +a\sin {frac {s} {\brt {a^{2}+b^{2} }}}}:\mathbf {j} +{\frac {bs}{\fracrt {a^{2}+b^{2} }}}}}\mathbf {k}
단위 접선 벡터는
d r d s = T = − a a 2 + b 2 죄 s a 2 + b 2 i + a a 2 + b 2 왜냐하면 s a 2 + b 2 j + b a 2 + b 2 k {\displaystyle {d\mathbf {r} {ds}}=\mathbf {T} = specfrac {-a}{\specrt {a^2}+b^{2} }}}}}\sin {\frac {s} {\fracrt {a^{2}+b^{2} }}}}\mathbf {i} +{\frac {a}{\fracrt {a^2}+b^{2} }}}}\cos {\frac {s}{\fracrt {a^{2}+b^{2} }}}}\mathbf {j} +{\frac {b}{\fracrt {a^2}+b^{2} }}}}}\mathbf {k}
정규 벡터는
d T d s = κ N = − a a 2 + b 2 왜냐하면 s a 2 + b 2 i + − a a 2 + b 2 죄 s a 2 + b 2 j + 0 k {\displaystyle {d\mathbf {T} {ds}}=\kappa \mathbf {N} = scfrac {-a} {a^{2}+b^{2} }}\cos {frac {s}{\frcrt {a^{2}+b^{2} }}}}\mathbf {i} +{\frac {-a}{a^{2}+b^{2} }}\sin {frac {s} {\fracrt {a^{2}+b^{2} }}}}:\mathbf {j} +0\mathbf {k} }
곡률은 d d s = θ = a b 2 displaystyle \ frac { d mathbf T } ds right kappa brac a } }}}}}.
단위 법선 벡터는
N = − 왜냐하면 s a 2 + b 2 i − 죄 s a 2 + b 2 j + 0 k {\displaystyle \mathbf {N} =-\cos {frac {s}{\csrt {a^{2}+b^{2} }}}}:\mathbf {i} -\sin {frac {s} {\sinrt {a^{2} + b^{2} }}}}:\mathbf {j} +0\mathbf {k} }
2정규 벡터는
B = T × N = 1 a 2 + b 2 [ b 죄 s a 2 + b 2 i − b 왜냐하면 s a 2 + b 2 j + a k ] {\displaystyle \mathbf {B} =\mathbf {T} \times \mathbf {N} =matsfrac {1}{\displaystyle {a^2}+b^{2} }}}}\left[b\sin {frac {s}{\synrt {a^{2}+b^{2} }}}}\mathbf {i}-b\cos {frac {s}{\csqrt {a^{2}+b^{2} }}}}:\mathbf {j} +a\mathbf {k} \right]}
d B d s = 1 a 2 + b 2 [ b 왜냐하면 s a 2 + b 2 i + b 죄 s a 2 + b 2 j + 0 k ] {\displaystyle {d\mathbf {B} {ds}} = flac {1} {a^{2} + b^{2} }}\left[b\cos {frac {s}{\ciscort {a^{2}+b^{2} }}}}:\mathbf {i} +b\sin {frac {s} {\synrt {a^{2} + b^{2} }}}}:\mathbf {j} +0\mathbf {k} \right]}
비틀림은 τ = d B s = b a2 b 2 displaystyle = left frac { d mathbf B } ds right dsfrac b a 2 b^ 2 }}}}}.
예 분자생물학에서 이중나선의 예는 핵산 이중나선 이다.
원뿔형 나선의 예로는 시더 포인트 놀이공원 의 코르크스크류 롤러코스터가 있습니다.
자연에서 발견된 일부 곡선은 서로 다른 손으로 만든 여러 개의 나선형으로 구성되어 있으며, 텐드릴 곡선 으로 알려진 전환에 의해 함께 결합되어 있습니다.
대부분의 하드웨어 나사산 은 오른손잡이 나선형입니다. 생물학의 알파나선은 물론 DNA의 A 와 B 형태도 오른손나선이다. DNA의 Z형 은 왼손잡이다.
음악 에서 피치 공간은 종종 나선형 또는 이중 나선형으로 모델링되며, 대부분의 경우 옥타브 등가를 나타내기 위해 5분의 1의 원 과 같은 원 밖으로 확장된다.
항공학에서 기하학적 피치는 비행기의 프로펠러 요소가 프로펠러 축에 수직인 평면과 현 사이의 각도와 동일한 각도를 가진 나선을 따라 이동할 경우 한 바퀴 회전하는 거리이다. 또한, 피치 각도(항행) 를 참조한다.
Helv의 Lehn 등이 보고 한 접힌 분자 나선의 결정 구조. 침, 액타, 2003, 86, 1598-1624.
「 」를 참조해 주세요. 무료 사전인 Wiktionary에서 helix를 찾아보세요
레퍼런스 ^ 2012-10-16 Wayback Machine에서의 아카이브 , 헨리 조지 리델, Robert Scott , 그리스 영어 렉시콘 , 페르세우스 관련^ Weisstein, Eric W. "Helicoid" . MathWorld ^ Wolfram 데모 프로젝트, Sandor Kabai의 「Wayback Machine에서의 Double Helix Archived 2008-04-30」.^ 오닐, B. 초등 미분 기하학, 1961 페이지 72^ 오닐, B. 초등 미분 기하학, 1961 페이지 74^ S. 이즈미야, N. 다케우치(2004) 새로운 특수 곡선과 전개 가능 한 표면. Turk J Math Archived 2016-03-04 Wayback Machine, 28:153–163.^ Menninger, T. (2013), 경사 나선형 Frenet 장치 의 명시적 매개변수화 . arXiv:1302. 3175 웨이백 머신에 2018-02-05 보관. ^ Weisstein, Eric W. "Helix" . MathWorld












![t\mapsto (a\cos t, a\sin t, bt), t\in [0,T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/93d3e0b26d648578d282662c605919e609ab3636)















![{\displaystyle \mathbf {B} =\mathbf {T} \times \mathbf {N} ={\frac {1}{\sqrt {a^{2}+b^{2}}}}\left[b\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} -b\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +a\mathbf {k} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be4cda61e31a02cb3b5034fb8342cfdeca40c466)
![{\displaystyle {\frac {d\mathbf {B} }{ds}}={\frac {1}{a^{2}+b^{2}}}\left[b\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} +b\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +0\mathbf {k} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/970c3b30b8f763a46e1575d5c3acfaaba210f1ba)