페르마의 나선

페르마의 나선형 또는 포물선은 나선형을 중심으로 연속적인 두 개의 완전한 턴 사이의 면적이 불변이라는 특성을 가진 평면 곡선입니다. 따라서 회전 사이의 거리는 나선 중심으로부터의 거리에 반비례하여 증가하는데, 이는 아르키메데스 나선(이 거리는 불변) 및 로그 나선(회전 사이의 거리는 중심으로부터의 거리에 비례함)과 대조됩니다. 페르마 나선은 피에르 드 페르마의 이름을 따서 붙여졌습니다.^[1]

이들의 응용 분야에는 곡선의 곡률 연속 혼합,^[1] 식물 성장 모델링 및 특정 나선 은하의 모양, 가변 커패시터, 태양열 전력 반사기 배열 및 사이클로트론 설계 등이 포함됩니다.

좌표표현

북극의

극좌표 $(r,$ φ)에서 페르마 나선의 표현은 다음 식으로 주어집니다.

r=\pma{\sqrt {\varphi}}

φ ≥ 0의 경우.

기호의 두 가지 선택은 원점에서 매끄럽게 만나는 나선형의 두 가지를 제공합니다. 만약 같은 변수를 데카르트 좌표로 재해석한다면, 이는 다시 축 위와 아래에 두 갈래가 원점에서 만나는 수평축을 가진 포물선의 방정식이 될 것입니다.

데카르트

극방정식을 가진 페르마 나선

r=\pma{\sqrt {\varphi}}

표준 변환 공식

x

= r

cos

φ 및 y = r sin φ을 사용하여 데카르트 좌표

(x,

y

)

로 변환할 수 있습니다. 이러한 변환에서

r

을 제거하기 위해 나선형에 대한 극성 방정식을 사용하면 곡선의 한 분기에 대한 모수 방정식이 생성됩니다.

{\begin{case}x(\varphi )=+a{\sqrt {\varphi}}\cos(\varphi)\y(\varphi)=+a{\sqrt {\varphi}\sin(\varphi)\end{case}}

그리고 두번째.

{\begin{case}x(\varphi)=-a{\sqrt {\varphi}}\cos(\varphi)\y(\varphi)=-a{\sqrt {\varphi}\sin(\varphi)\end{case}}

이들은 $모수$ φ가 양수의 실수 범위에 걸쳐 있으므로 곡선의 분기점을 생성합니다.

이렇게 생성된 임의의 ( $x,$ y $)$ 에 대해 $x$ 를 $y$ 로 나누면 모수 $방정식$ 의 a √φ 부분이 상쇄되어 더 간단한 $방정식$ x/ $y$ = cot φ가 됩니다. $이$ 방정식에서 φ를 φ = r/a (나선에 대한 극 방정식의 재배열된 형태)로 대체한 다음 r을 $r$ = √x + y (데카르트에서 극으로 변환)로 대체하면 x와 y의 관점에서 페르마 나선에 대한 방정식이 남게 됩니다.

{\displaystyle {\frac {x}{y}}=\cot \left ({\frac {x^{2}+y^{2}}{a^{2}}\right).

a

의 부호는 제곱하면 사라지기 때문에 이 방정식은 곡선의 두 갈래를 모두 포함합니다.

기하학적 성질

페르마의 나선은 평면을 연결되어 있고 합동인 두 영역(그림: 흑백)으로 나눕니다.

비행기의 나눗셈

완전한 페르마의 나선(양가지)은 아르키메데스와 쌍곡 나선과 대조적으로 매끄러운 이중점 자유 곡선입니다. 선이나 원, 포물선처럼 평면을 두 개의 연결된 영역으로 나눕니다.

극경사

극좌표의 벡터 미적분학에서 공식을 얻습니다.

\tan \alpha = {\frac {r'}{r}

극기울기와 곡선의 접선과 대응하는 극원 $사이$ 의 각도 α의 경우(그림 참조).

$페르마$ 의 $나선형$ r = √φ에 대하여

{\displaystyle \tan \alpha = {\frac {1}{2\varphi}}.

따라서 기울기 각도가 단조롭게 감소합니다.

곡률

공식으로부터

\kappa ={\frac {r^{2}+2(r')^{2}-r\,r''}{\left(r^{2}+(r')^{2}\right)^{\frac {3}{2}}}}

극방정식 $r$ = $r$ (φ)과 그 도함수를 갖는 곡선의 곡률에 대하여

{\begin{aligned}r'&={\frac {a}{2{\sqrt {\varphi }}}}={\frac {a^{2}}{2r}}\\r''&=-{\frac {a}{4{\sqrt {\varphi }}^{3}}}=-{\frac {a^{4}}{4r^{3}}}\end{aligned}}

페르마의 나선의 곡률을 구합니다.

\kappa (r)={\frac {2r\left(4r^{4}+3a^{4}\right)}{\left(4r^{4}+a^{4}\right)^{\frac {3}{2}}}}.

원점에서 곡률은 0입니다. 따라서 완전 곡선은 원점에 변곡점이 있고 x축은 접선이 됩니다.

호 사이의 면적

페르마 나선의 두 점 ( $r ($ φ),φ)과 (r(φ), φ) 사이의 영역의 넓이는

{\begin{aligned}{\underline {A}}&={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}r(\varphi )^{2}\,d\varphi \\&={\frac {1}{2}\int _{\varphi _{1}}^{\varphi \,d\varphi \\&={\frac {a^{2}}{4}\left(\varphi _{2}^{2}-\varphi _{1}^{2}\right)\\&={\frac {a^{2}}{4}}\left(\varphi_{2}+\varphi_{1}\right)\left(\varphi_{2}-\varphi_{1}\right).\end{align}}

양쪽 각도를 $2$ π 올린 후에 하나를 얻습니다.

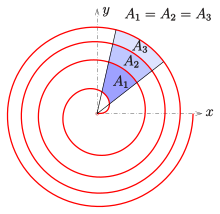
{\overline {A}}={\frac {a^{2}}{4}}\left(\varphi_{2}+\varphi_{1}+4\pi \right)\left(\varphi_{2}-\varphi_{1}\right)={\underline {A}+a^{2}\pi \left(\varphi _{2}-\varphi _{1}\right)

따라서 이웃한 두 호 사이의 영역 $A는$

A=a^{2}\pi \left(\varphi_{2}-\varphi_{1}\right)

A

는 각도 자체에 의존하지 않고 두 각도의 차이에만 의존합니다.

다이어그램에 표시된 예에서 모든 인접 스트라이프의 면적은 동일합니다. $A =$ A $=$ A.

이 특성은 가변 커패시터 구성을 위한 전기 공학에 사용됩니다.^[2]

페르마로 인한 특별한 경우

1636년 페르마는 마린 메르센에게 다음과 같은 특별한 경우를 담은 편지를 썼습니다.

φ = $0$ , φ = 2 π라고 하자. 그러면 검은 영역( $그림$ 참조)의 면적은 A = a이며, 이는 반지름이 r(π)인 원 $K$ 의 $면적$ 의 절반입니다. 이웃한 곡선 사이의 영역(흰색, 파란색, 노란색)은 $동일$ 한 면적 A = $2a$ π을 갖습니다. 따라서:

완전히 회전한 후 나선의 두 호 사이의 면적은 원 $K$ 의₀ 면적과 같습니다.

호 길이

두 점 $(r ($ φ), φ) 사이의 페르마 나선의 호 길이는 적분으로 계산할 수 있습니다.

{\begin{aligned}L&=\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {\left(r^{\prime }(\varphi )\right)^{2}+r^{2}(\varphi )}\,d\varphi \\&={\frac {a}{2}\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {{\frac {1}}{\varphi }+4\varphi }}\,d\varphi .\end{aligned}}

이 적분은 타원 적분으로 이어지고, 이것은 수치적으로 해결될 수 있습니다.

원점에서 페르마 나선의 양의 가지의 호 길이는 또한 초기하 $함수 1$ F $(a,$ $b$ ; $c$ ; $z)$ 와 불완전 베타 $함수$ B( $z;$ a, $b$ )에 의해 정의될 수 있습니다 $.$ ^[4]

{\begin{aligned}L&=a\cdot {\sqrt {\varphi }}\cdot \operatorname {_{2}F_{1}} \left(-{\tfrac {1}{2}},\,{\tfrac {1}{4}};\,{\tfrac {5}{4}};\,-4\cdot \varphi ^{2}\right)\\&=a\cdot {\frac {1-i}{8}}\cdot \operatorname {B} \left(-4\cdot \varphi ^{2};\,{\tfrac {1}{4}},\,{\tfrac {3}{2}}\right)\\\end{aligned}}

원 반전

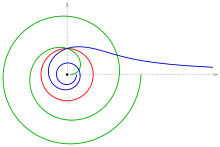
단위 원에서의 반전은 극좌표에서 단순한 설명 $(r,$ φ $)$ ↦(1/r, φ)을 갖습니다.

페르마의 나선 $r$ = 단위원에서의 반전 $아래$ 의√φ의 상은 극방정식을 가진 쌍곡선입니다. ${\displaystyle r={\frac {1}{a{\sqrt {\varphi}}}}.$ φ = $1$ /a인 경우 두 곡선은 단위 원의 고정된 점에서 교차합니다.
페르마 나선의 변곡점(기점)에 있는 접선(x축)은 자신과 매핑되며, 리투우스 나선의 점근선입니다.

황금비율과 황금각.

디스크 필로택스에서 해바라기와 데이지와 마찬가지로 나선의 메시는 발산(단일 나선 배열에서의 연속 각도)이 황금 비율에 접근하기 때문에 피보나치 수에서 발생합니다. 나선의 모양은 순차적으로 생성되는 원소의 성장에 따라 달라집니다. 모든 원소의 크기가 같을 때, 원뿔의 모양은 이상적으로 페르마 원뿔의 모양입니다. 그것은 페르마의 나선이 등회전으로 같은 고리를 가로지르기 때문입니다. 1979년^[5] H. Vogel이 제안한 전체 모델은

{\begin{aligned}r&=c{\sqrt {n}},\\theta &=n\times 137.508^{\circ},\end{aligned}

$여기$ 서 θ는 각도, r은 $중심$ 으로부터의 반경 또는 거리, n은 $플로렛$ 의 인덱스 번호, c는 일정한 스케일링 팩터입니다. 각도 137.508°는 피보나치 수의 비율로 근사한 황금각입니다.^[6]

Vogel의 모델(중심 이미지)에 의해 생성된 플로렛의 패턴. 다른 두 이미지는 각도의 약간 다른 값에 대한 패턴을 보여줍니다.

단위 디스크의 나선형 패턴은 로그 나선형 위에 기하학적으로 증가하는 반지름의 접선 디스크에 의해 형성되는 패턴인 도일 나선형과 구별되어야 합니다.

태양열 식물

페르마의 나선형은 또한 집중된 태양열 발전소의 거울을 위한 효율적인 배치임이 밝혀졌습니다.^[7]

참고 항목

참고문헌

^ ^a ^b Lekkas, Anastasios M.; Dahl, Andreas R.; Breivik, Morten; Fossen, Thor I. (2013). "Continuous-Curvature Path Generation Using Fermat's Spiral" (PDF). Modeling, Identification and Control. 34 (4): 183–198. ISSN 1890-1328. Archived from the original (PDF) on 2020-10-28.
^ Wicke, Fritz (2013). Einführung in die höhere Mathematik. Springer-Verlag. p. 414. ISBN 978-3-662-36804-6.
^ Tannery, Paul (ed.). "Lettre de Fermat à Mersenne du 3 juin 1636". Œuvres de Fermat. Vol. 3. p. 277.
^ Weisstein, Eric W. "Fermat's Spiral". MathWorld. Retrieved 2023-02-04.
^ Vogel, H. (1979). "A better way to construct the sunflower head". Mathematical Biosciences. 44 (3–4): 179–189. doi:10.1016/0025-5564(79)90080-4.
^ Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990). The Algorithmic Beauty of Plants. Springer-Verlag. pp. 101–107. ISBN 978-0-387-97297-8.
^ Noone, Corey J.; Torrilhon, Manuel; Mitsos, Alexander (December 2011). "Heliostat Field Optimization: A New Computationally Efficient Model and Biomimetic Layout". Solar Energy. 86 (2): 792–803. doi:10.1016/j.solener.2011.12.007.

외부 링크

[Lekkas-1] Lekkas, Anastasios M.; Dahl, Andreas R.; Breivik, Morten; Fossen, Thor I. (2013). "Continuous-Curvature Path Generation Using Fermat's Spiral" (PDF). Modeling, Identification and Control. 34 (4): 183–198. ISSN 1890-1328. Archived from the original (PDF) on 2020-10-28.

[2] Wicke, Fritz (2013). Einführung in die höhere Mathematik. Springer-Verlag. p. 414. ISBN 978-3-662-36804-6.

[Fermat-3] Tannery, Paul (ed.). "Lettre de Fermat à Mersenne du 3 juin 1636". Œuvres de Fermat. Vol. 3. p. 277.

[4] Weisstein, Eric W. "Fermat's Spiral". MathWorld. Retrieved 2023-02-04.

[5] Vogel, H. (1979). "A better way to construct the sunflower head". Mathematical Biosciences. 44 (3–4): 179–189. doi:10.1016/0025-5564(79)90080-4.

[6] Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990). The Algorithmic Beauty of Plants. Springer-Verlag. pp. 101–107. ISBN 978-0-387-97297-8.

[7] Noone, Corey J.; Torrilhon, Manuel; Mitsos, Alexander (December 2011). "Heliostat Field Optimization: A New Computationally Efficient Model and Biomimetic Layout". Solar Energy. 86 (2): 792–803. doi:10.1016/j.solener.2011.12.007.

[1]

[2]

[4]

[5]

[6]

[7]

v t 피에르 드 페르마
일하다.	페르마의 마지막 정리 페르마 수 페르마의 원리 페르마의 작은 정리 페르마 다각수 정리 페르마 의사 소수 페르마 점 페르마 정리(정지점) 두 제곱의 합에 관한 페르마의 정리 페르마의 나선 페르마의 직각삼각형 정리
관련된	피에르 드 페르마의 이름을 딴 목록 와일스의 페르마의 마지막 정리 증명 소설 속 페르마의 마지막 정리 페르마상 페르마의 마지막 탱고 (2000 뮤지컬) 페르마의 마지막 정리 (대중 과학 서적)

Search