대칭(지오메트리)

Symmetry (geometry)
좌우 대칭으로 나비를 그린 그림으로, 좌우 대칭이 서로 거울처럼 보인다.

기하학에서 물체는 그림/물체를 자신에게 매핑하는 작동이나 변환(번역, 스케일링, 회전 또는 반사 등)이 있을 경우 대칭을 가진다(즉, 물체는 변환 아래에 불변성을 가진다).[1] 따라서 대칭은 변화에 대한 면역으로 생각할 수 있다.[2] 예를 들어, 중심 주위를 회전하는 원은 변환 전과 후의 모든 점이 구별할 수 없는 것처럼 원래 원과 동일한 모양과 크기를 가질 것이다. 따라서 원은 회전할 때 대칭이거나 회전 대칭을 갖는다고 한다. 등각도가 선에 대한 평면 형상의 반영이라면, 그 형상은 반사 대칭 또는 선 대칭을 가지고 있다고 한다.[3] 그림/물체가 둘 이상의 대칭선을 갖는 것도 가능하다.[4]

기하학적 객체에 대해 가능한 대칭의 유형은 사용 가능한 기하학적 변환 집합과 변환 후에도 변경되지 않아야 하는 객체 속성에 따라 달라진다. 왜냐하면 두 변환의 구성도 하나의 변환이고 모든 변환은 정의상 그것을 풀 수 있는 역 변환을 가지고 있기 때문에, 어떤 물체가 대칭으로 되어 있는 변환 집합은 그 개체의 대칭 그룹인 수학적 그룹을 형성한다.[5]

일반적으로 유클리드 대칭

물체에 적용되는 가장 일반적인 변환 그룹은 "등각류"의 유클리드 그룹으로, 일반적으로 2차원 또는 3차원(즉 평면 기하학 또는 고체 기하학 유클리드 공간)으로 언급되는 공간에서의 거리 보존 변환이다. 이 등각계는 반사, 회전, 변환 및 이러한 기본 운영의 조합으로 구성된다.[6] 등축 변환에서 기하학적 객체는 변환 후 객체와 변환 전 객체를 구분할 수 없는 경우 대칭이라고 한다.[7] 기하학적 물체는 일반적으로 모든 등각도의 부분 집합 또는 "하위 그룹"에서만 대칭이다. 이등계 부분군의 종류는 아래에 설명되어 있으며, 그 다음에 다른 종류의 변환 그룹, 그리고 기하학에서 가능한 물체 불변성의 유형으로 설명되어 있다.

카르탄-디우도네 정리(Cartan-Dieudonné)에 의해 n차원 공간의 직교 변환은 최대 n개의 반사의 구성으로 나타낼 수 있다.

치수별 기본 등각도
1D 2D 3D 4D
반사 포인트 아핀 포인트 아핀 포인트 아핀 포인트 아핀
1 반사 반사 반사 반사
2 번역 회전 번역 회전 번역 회전 번역
3 수혈 로토레선택 수혈 로토레선택 수혈
4 로터리 번역 이중 회전 로터리 번역
5 회전수혈

반사대칭

주요기사 : 반사대칭

반사 대칭, 선형 대칭, 거울 대칭, 거울 대칭, 거울-이미지 대칭 또는 양자 대칭은 반사에 대한 대칭이다.[8]

한 차원에는 반사가 일어나는 대칭점이 있고, 두 차원에는 대칭의 축(즉, 대칭의 선)이 있고, 세 차원에는 대칭의 평면이 있다.[3][9] 모든 점이 공통 평면의 반대편과 반대편에서 다른 점으로 일대일 매핑되는 객체 또는 도형을 미러 대칭(더 자세한 내용은 미러 이미지 참조)이라고 한다.

2차원 형상의 대칭축은 수직이 구성되면 대칭축으로부터 같은 거리에서 수직에 놓여 있는 두 점이 동일한 선이다. 또 한 가지 생각해 볼 수 있는 방법은 만약 그 모양이 축 위에 반으로 접혀진다면, 두 반쪽은 서로 거울의 이미지와 똑같을 것이다. 예를 들어, 사각형은 4개의 대칭 축을 가지고 있는데, 그것은 그것을 접는 네 가지 다른 방법이 있고 가장자리가 서로 일치하기 때문이다. 또 다른 예는 같은 이유로 그 중심을 통과하는 대칭의 축이 무한히 많은 원의 그것일 것이다.[10]

문자 T가 수직축을 따라 반사되면 똑같이 나타난다. 이것을 수직 대칭이라고 부르기도 한다. 따라서 "T는 수직 대칭 축을 가지고 있다"거나 "T는 좌우 대칭 축을 가지고 있다"고 말해 이 현상을 명쾌하게 설명할 수 있다.

반사 대칭이 있는 삼각형은 이소체, 이 대칭이 있는 사분면 측정은 연과 이소체 사다리꼴이다.[11]

각 선이나 반사 평면에 대해 대칭 그룹은 C와s 이형이며(3차원의 점 그룹 참조), 순서 2의 세 가지 유형 중 하나(인볼루션), 따라서 C에2 대해 대수적으로 이형성이다. 기본 도메인은 반평면 또는 반평면이다.[12]

점 반사 및 기타 비자발적 등위계

2차원에서 점 반사는 180도 회전이다.
주요기사 : 점반사

반사 대칭은 다음과 같이 비자발적인 m-차원 공간의 다른 등축에 일반화될 수 있다.

(x1, ..., xm) ↦ (-x1, ..., -xk, x, xk+1m)

데카르트 좌표계의 특정 체계로 말이야 이것은 (m-k)차원 아핀 하위 공간을 따라 공간을 반영한다.[13] k = m인 경우, 그러한 변환을 점 반사 또는 점을 통한 반전이라고 한다. 평면(m = 2)에서 점 반사는 반 바퀴(180°)와 같다. 회전; 아래 참조. 대칭은 원점을 통한 점 반사 대칭의 대체 명칭이다.[14]

이러한 "반성"은 k가 짝수일 경우에만 방향을 보존한다.[15] 이는 m = 3(다른 홀수 m도 마찬가지)의 경우 점 반사가 거울-이미지 대칭과 같이 공간의 방향을 변화시킨다는 것을 의미한다. 그래서 물리학에서 P-대칭(P는 패리티를 나타낸다)이라는 용어가 점반사와 거울 대칭 모두에 사용되는 것이다. 3차원의 점반사는 좌표계를 우표 좌표계로 변화시키기 때문에 점반사 아래의 대칭을 좌우 대칭이라고도 한다.[16]

회전대칭

주요기사 : 회전대칭
트리스켈리온은 3배 회전 대칭이다.

회전 대칭은 m-차원 유클리드 공간의 일부 또는 전체 회전과 관련된 대칭이다. 회전은 방향성을 보존하는 등각류인 직접 등각각은 방향성을 보존하는 직등분법이다.[17] 따라서 회전 대칭의 대칭 그룹은 특수 유클리드 그룹 E+(m)의 하위 그룹이다.

모든 점에 대한 모든 회전과 관련된 대칭은 모든 번역에 대한 변환 대칭을 내포하고 있다(왜냐하면 번역은 구별되는 점에 대한 회전 구성이기 때문),[18] 대칭 그룹은 전체 E+(m)이다. 이것은 공간을 동질적으로 만들기 때문에 물체에는 적용되지 않지만, 물리적 법칙에는 적용될 수 있다.

점의 회전과 관련된 대칭성의 경우, 그 점을 원점으로 삼을 수 있다. 이러한 회전은 특수 직교 그룹 SO(m)를 형성하며, 결정인자가 1인 m × m 직교 행렬 그룹으로 나타낼 수 있다. m = 3의 경우, 이것은 회전 그룹 SO(3)이다.[19]

약간 다르게 표현된 물체의 회전 그룹은 E+(m) 내의 대칭 그룹, 즉 전체 대칭 그룹과 경직된 움직임 그룹의 교차점이다.[20] 키랄 개체의 경우 전체 대칭 그룹과 동일하다.

물리 법칙은 우주에서 서로 다른 방향을 구분하지 않으면 SO(3) 불변이다. 노에더의 정리 때문에 물리적 시스템의 회전 대칭은 각운동량 보존법과 동등하다.[21] 자세한 내용은 회전 불변도를 참조하십시오.

변환 대칭

변환 대칭이 있는 프리제 패턴
주요 기사: 변환 대칭

대칭은 T ()= + 의 이산 또는 연속적인 그룹 아래 불변하는 물체를 남긴다[22] 에는 화살표를 따라 번역에 의해 생성된 4개의 일치된 발자국이 표시된다 만약 발자국의 선이 양방향으로 무한대로 확장된다면, 그들은 분리된 변환 대칭을 가질 것이다; 한 발자국을 다른 자국에 매핑하는 어떤 번역도 전체 선을 변경하지 않을 것이다.

글라이드 반사 대칭

글라이드 반사 대칭이 있는 프리제 패턴
주요기사 : 글라이드 반사

2D에서 글라이드 반사 대칭(3D에서는 글라이드 평면 대칭이라고도 하며, 일반적으로 수혈이라고도 함)은 선이나 평면에 있는 번역과 결합된 선이나 평면의 반사가 같은 물체(발자국의 경우 등)를 낳는 것을 의미한다.[2][23] 두 글라이드 반사의 구성은 번역 벡터의 두 배로 번역 대칭을 이룬다. 글라이드 반사 및 관련 번역으로 구성된 대칭 그룹은 프리제 그룹 p11g이며, 무한 순환 그룹 Z와 이형성이다.

회전 대칭

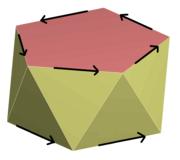
가장자리가 표시된 오각형 항정신병증은 10의 순서에 따라 회전 대칭이 나타난다.
주요기사 : 부적절한 회전

3D에서 회전 반사, 회전 선택 또는 부적절한 회전은 축에 수직인 평면에서 반사된 것과 결합된 축을 중심으로 회전하는 것이다.[24] 회전 편향과 관련된 대칭 그룹은 다음과 같다.

  • 회전 각도에 360°의 공통 분비가 없는 경우 대칭 그룹은 이산되지 않는다.
  • 회전각(Rotoreflection)이 2n배 회전각(각 180°/n)인 경우 S이다2n(동일한 표기법을 사용하는 대칭 그룹과 혼동해서는 안 되며 추상 그룹은 C이다2n)순서 2n의 대칭군은. 특별한 경우는 축과 평면에 의존하지 않기 때문에 n = 1, 반전이다. 그것은 단지 역전의 지점이 특징적이다.
  • 그룹 Cnh (360°/n의 각도); 홀수 n의 경우 이것은 단일 대칭에 의해 생성되며, 추상 그룹은 짝수 n에 대해 C이다2n. 이것은 기본 대칭이 아니라 조합이다.

자세한 내용은 3차원의 점 그룹을 참조하십시오.

헬리컬 대칭

참고 항목: 나사 축

3D 기하학 이상에서 나사 축(또는 회전 변환)은 회전 축을 따라 회전하는 것과 변환하는 것의 조합이다.[25]

헬리컬 대칭은 스프링, 슬링키 장난감, 드릴 비트, 인어스터와 같은 일상적인 물체에서 볼 수 있는 대칭의 일종이다. 나선대칭의 개념은 물체를 일정한 각도 속도로 회전하면서 동시에 회전축을 따라 일정한 선형 속도로 변환하는 데서 비롯되는 3차원 공간의 추적으로 시각화할 수 있다. 어느 시점에서든 이 두 동작이 결합되어 추적된 나선형의 성질을 정의하는 데 도움이 되는 코일 각도를 제공한다.[26] 추적 물체가 빠르게 회전하고 천천히 번역하면 코일 각도가 0°에 가까워진다. 반대로 물체가 천천히 회전하여 빠르게 번역하면 코일각은 90°에 근접하게 된다.

연속나선

축을 따라 코일링 각도와 변환 대칭의 상호작용을 바탕으로 나선형 대칭의 세 가지 주요 클래스를 구별할 수 있다.

일반 스큐-아페이로곤은 원근법으로 그려진 분리된(여기서 3배) 나사축 대칭을 가지고 있다.
보어디크-콕시터 나선형(Boerdijk-Coxeter helix)은 증강정규정 사트라헤드라에 의해 구축된 것으로, 비주기적인 나사 축 대칭의 예다.
  • 무한 나선형 대칭: 나선형이나 나선형 같은 물체의 길이를 따라 구별되는 특징이 없다면, 물체는 원의 그것과 매우 유사하지만, 물체의 긴 축을 따라 번역해야 하는 추가 요건으로 인해 무한한 대칭성을 가지게 될 것이다. 즉, 원래의 모습으로 되돌리기 위해서 말이다.[27] 나선형 모양의 물체는 나선형의 코일링의 정규 각도를 모든 지점에 가지고 있지만, 물체의 길이를 따라 모든 지점에 정확하게 동일한 단면(보통 회전 후)이 존재한다면 무한히 높은 복잡도의 단면을 가질 수 있는 물체다. 간단한 예로는 고르게 코팅된 스프링, 슬링키, 드릴 비트, 어거스트가 있다. 보다 정확히 말하면, 물체는 중심축 주위의 물체의 작은 회전에 대해 그 축에 물체가 이전처럼 정확하게 나타나는 점(번역 거리)이 존재한다면 무한한 나선 대칭성을 가진다. 회전하고 있는 오거나 나사 비트의 길이를 따라 움직이는 기이한 착각을 불러일으키는 것이 바로 이 무한 나선 대칭이다. 또한 그러한 장치가 드릴이나 오거와 함께 단순히 회전하는 것에 저항할 수 있는 중력이나 마찰과 같은 힘과 결합되어 있다면, 그러한 장치들이 길이를 따라 물질을 이동시키는 기계적으로 유용한 능력을 제공한다.
  • n-폴드 나선형 대칭: 나선형 물체의 모든 단면이 동일해야 한다는 요건이 완화되면, 더 적은 나선형 대칭이 추가로 가능해진다. 예를 들어 헬리컬 객체의 단면은 변경될 수 있지만, 헬리컬 객체의 축을 따라 규칙적으로 반복될 수 있다. 결과적으로, 이 형식의 물체는 일정한 각도 by에 의한 회전과 일정한 거리에 의한 변환 후에 대칭을 나타낼 것이지만, 일반적으로 어떤 회전 각도에 대해서도 불변하지는 않을 것이다. 대칭이 발생하는 회전각이 전체 원(360°)으로 고르게 분할되면 그 결과는 일반 다각형에 해당하는 나선형 등가 된다. 이 경우를 n-폴드 나선대칭이라고 하는데 여기서 n = 360°(이중나선의 경우 등)이다. 개념은 m 이(가) 360°의 배수인 경우를 포함하도록 더 일반화할 수 있다. 즉, 주기는 결국 반복되지만 나선형 물체를 두 번 이상 완전히 회전한 후에만 반복된다.
  • 반복되지 않는 나선 대칭: 대칭을 관찰하는 데 필요한 회전각 θ이 비합리적인 경우다. 회전각은 나선이 아무리 회전해도 정확하게 반복되지 않는다. 이러한 대칭은 2차원에서 반복되지 않는 점 그룹을 사용하여 생성된다. 턴당 약 10.5개의 염기쌍이 있는 DNA는 이러한 유형의 비반복 나선대칭의 예다.[28]

이중 회전 대칭

입체적으로 3D에 투영된 4D 클리포드 토루스는 토러스처럼 보인다. 이중 회전은 나선 경로로 볼 수 있다.
참고 항목: 4차원 유클리드 공간의 회전 § 이중 회전

4D에서는 두 직교 회전의 합성어로 이중 회전 대칭이 생성될 수 있다.[29] 회전과 직교 번역을 합친 3D 스크루 축과 비슷하다.

비등각 대칭

기하학적 대칭에 대한 넓은 정의는 유클리드 그룹의 등위계 그룹보다 더 큰 그룹으로부터의 연산을 허용한다. 더 큰 기하학적 대칭 그룹의 예는 다음과 같다.

펠릭스 클라인의 에를랑겐 프로그램에서 각각의 가능한 대칭 그룹은 대칭 그룹의 구성원에 의해 관련되는 물체가 등가물로 간주되는 기하학을 정의한다.[32] 예를 들어 유클리드 집단은 유클리드 기하학을 정의하는 반면, 뫼비우스 변환 집단은 투영적 기하학을 정의한다.

척도 대칭 및 프랙탈

줄리아 집합은 척도 대칭을 가지고 있다.

척도 대칭이란 물체가 확대되거나 크기가 줄어들면 새 물체는 원래 물체와 동일한 성질을 갖는다는 것을 의미한다.[33] 코끼리와 쥐의 다리 모양(일명 알로미터 스케일링)의 차이를 목격하는 것처럼 대부분의 물리적 시스템에서는 그렇지 않다. 마찬가지로 부드러운 왁스 초를 키 큰 나무 크기로 확대하면 곧바로 자신의 무게로 무너진다.

보다 미묘한 형태의 척도 대칭은 프랙탈에 의해 증명된다. Benoît Mandelbrot에 의해 구상된 것처럼 프랙탈은 복잡한 형태의 구조가 어느 정도의 확대에서도 비슷해 보이는 수학 개념으로, 만델브로트 세트에서 잘 볼 수 있다.[34] 해안은 자연적으로 발생하는 프랙탈의 한 예로서, 인공위성의 관점에서부터 물이 모래의 개별 알갱이에 대해 어떻게 흘러들어가는지에 대한 현미경 검사까지 모든 수준에서 유사하게 나타나는 복잡성을 지니고 있기 때문이다. 작은 나뭇가지들이 디오라마에 가득찬 나무들을 위해 서 있을 수 있게 하는 나뭇가지도 또 다른 예다.

프랙탈은 자연에서 패턴의 외관을 만들어낼 수 있기 때문에 수학적으로 생성되는 기능으로는 일반적으로 볼 수 없는 아름다움과 친숙함을 가지고 있다. 프랙탈은 또한 프랙탈 대칭으로 복잡한 곡선을 만드는 능력이 더 현실적인 가상세계를 만들어 내는 컴퓨터로 만들어진 영화 효과에서 자리를 찾았다.

추상대칭

클라인의 견해

모든 기하학에서 펠릭스 클라인은 밑바탕에 깔린 대칭들을 연결했다. 따라서 기하학의 계층 구조는 수학적으로 이러한 집단의 계층 구조와 불변성의 계층 구조로 표현된다. 예를 들어 유클리드 대칭 그룹에 관해서 길이, 각도 및 영역이 보존되는 반면, 발생 구조와 교차 비율만 가장 일반적인 투영적 변환에 의해서 보존된다. 아핀 기하학에서 보존되는 병렬 개념은 투영 기하학에서는 의미가 없다. 그런 다음, 기하학에서 대칭의 기본 그룹을 추상화함으로써, 그 사이의 관계는 그룹 수준에서 다시 설정될 수 있다. 아핀 기하학 그룹은 투영 기하학 그룹의 하위 그룹이기 때문에, 투영 기하학에서 불변하는 개념은 아핀 기하학에서 의미 있는 선험적인 것이다. 그러나 다른 방법은 아니다. 필요한 대칭을 더하면 더 강력한 이론이 있지만 개념과 정리(더 깊고 일반적이 될 것)가 적다.

서스턴의 견해

윌리엄 서스턴은 기하학에서 유사한 버전의 대칭을 소개했다. 모델 지오메트리는 X에서 콤팩트한 스태빌라이저로 리 그룹 G의 전이 작용과 함께 단순하게 연결된 매끄러운 다지관 X이다. Lie 그룹은 지오메트리의 대칭 그룹이라고 생각할 수 있다.

모델 지오메트리는 콤팩트한 안정기로 X에서 부드럽고 트랜스적으로 작용하는 그룹들, 즉 대칭의 최대 그룹인 경우 최대값이라고 한다. 때때로 이 조건은 모델 기하학의 정의에 포함된다.

다지관 M의 기하학적 구조는 일부 모델 기하학 X에 대해 M에서 X/TW까지의 차이점형 구조로, 여기서 γ은 X에 자유롭게 작용하는 G의 이산형 부분군이다. 만약 주어진 다지관이 기하학적 구조를 인정한다면, 그것은 그 모델이 최대인 사람을 인정한다.

3차원 모델 지오메트리 X는 그것이 최대인지 그리고 X에 모델링된 기하학적 구조를 가진 하나 이상의 콤팩트 매니폴드가 있는지 기하학적 추측과 관련이 있다. Thurston은 이러한 조건을 만족하는 8가지 모델 기하학을 분류했다; 그것들은 아래에 나열되어 있고 때때로 Thurston 기하학이라고 불린다. (소형 인용구를 포함하지 않은 모델 기하학도 셀 수 없을 만큼 많다.

참고 항목

참조

  1. ^ Martin, G. (1996). Transformation Geometry: An Introduction to Symmetry. Springer. p. 28.
  2. ^ a b "Symmetry Thinking about Geometry Underground Mathematics". undergroundmathematics.org. Retrieved 2019-12-06.
  3. ^ a b "Symmetry - MathBitsNotebook(Geo - CCSS Math)". mathbitsnotebook.com. Retrieved 2019-12-06.
  4. ^ Freitag, Mark (2013). Mathematics for Elementary School Teachers: A Process Approach. Cengage Learning. p. 721.
  5. ^ Miller, Willard Jr. (1972). Symmetry Groups and Their Applications. New York: Academic Press. OCLC 589081. Archived from the original on 2010-02-17. Retrieved 2009-09-28.
  6. ^ "Higher Dimensional Group Theory". Archived from the original on 2012-07-23. Retrieved 2013-04-16.
  7. ^ "2.6 Reflection Symmetry". CK-12 Foundation. Retrieved 2019-12-06.
  8. ^ Weyl, Hermann (1982) [1952]. Symmetry. Princeton: Princeton University Press. ISBN 0-691-02374-3.
  9. ^ Cowin, Stephen C.; Doty, Stephen B. (2007). Tissue Mechanics. Springer. p. 152.
  10. ^ Caldecott, Stratford (2009). Beauty for Truth's Sake: On the Re-enchantment of Education. Brazos Press. p. 70.
  11. ^ Bassarear, Tom (2011). Mathematics for Elementary School Teachers (5 ed.). Cengage Learning. p. 499.
  12. ^ Johnson, N. W. Johnson (2018). "11: Finite symmetry groups". Geometries and Transformations. Cambridge University Press.
  13. ^ Hertrich-Jeromin, Udo (2003). Introduction to Möbius Differential Geometry. Cambridge University Press.
  14. ^ Dieck, Tammo (2008). Algebraic Topology. European Mathematical Society. pp. 261. ISBN 9783037190487.
  15. ^ 윌리엄 H. 바커, 로저 하우 연속 대칭: 유클리드부터 클라인까지(구글 eBook) 미국수학협회
  16. ^ W.M. Gibson & B.R. Pollard (1980). Symmetry principles in elementary particle physics. Cambridge University Press. pp. 120–122. ISBN 0 521 29964 0.
  17. ^ 블라디미르 G. 이반체비치, 티자나 T. 이반체비치(2005) 자연생물역학 세계과학
  18. ^ Singer, David A. (1998). Geometry: Plane and Fancy. Springer Science & Business Media.
  19. ^ Joshi, A. W. (2007). Elements of Group Theory for Physicists. New Age International. pp. 111ff.
  20. ^ Hartshorne, Robin (2000). Geometry: Euclid and Beyond. Springer Science & Business Media.
  21. ^ Kosmann-Schwarzbach, Yvette (2010). The Noether theorems: Invariance and conservation laws in the twentieth century. Sources and Studies in the History of Mathematics and Physical Sciences. Springer-Verlag. ISBN 978-0-387-87867-6.
  22. ^ 스텐거, 빅터 J(2000년), 마후 시로(2007년). 타임리스 리얼리티. 프로메테우스 북스. 특히 12장. 비기술적.
  23. ^ Martin, George E. (1982), Transformation Geometry: An Introduction to Symmetry, Undergraduate Texts in Mathematics, Springer, p. 64, ISBN 9780387906362.
  24. ^ 로버트 O. 굴드, Steffen Borchardt-Ot(2011) Crystallography: 소개 스프링어 과학 & 비즈니스 미디어
  25. ^ 보테마, O, B. 로스, 이론 운동학, 도버 출판물 (1990년 9월)
  26. ^ 조지 R. 맥기희(2006) 진화의 기하학: Cambridge University 출판부 p.64
  27. ^ Anna Ursyn(2012) 생물학적으로 영감을 받은 예술용 컴퓨팅: 그래픽 IGI 글로벌 코드 조각 p.209[clarification needed]
  28. ^ Sinden, Richard R. (1994). DNA structure and function. Gulf Professional Publishing. p. 101. ISBN 9780126457506.
  29. ^ 찰스 하워드 힌튼 (1906) The Four Dimension (Google eBook) S. 손넨샤인 & 컴퍼니 p.223
  30. ^ H.S.M. Coxeter(1961,9) 기하학 소개, §5 유클리드 평면의 유사성, 페이지 67–76, §7 유클리드 공간에서의 이소메트리 및 유사성, 페이지 96–104, 페이지 존 와일리 & Sons.
  31. ^ 윌리엄 서스턴 3차원 기하학 및 위상. 제1권. 실비오 레비에 의해 편집된다. 프린스턴 수학 시리즈, 35. 프린스턴 대학 출판부, 프린스턴, NJ, 1997. x+311 페이지 ISBN 0-691-08304-5
  32. ^ 1872년 클라인, 펠릭스 "Vergleichende Betrachtungen über neuere 기하학 Forschungen" ('기하학 연구에 대한 최근 연구의 비교 검토') Matheatische Annalen, 43 (1893) pp. 63–100 (또한: Gesammelte Abh) 제1권, 스프링거, 1921권, 페이지 460-497).
    Mellen Haskell의 영어 번역본이 Bull에 등장했다. N. Y. 수학. Soc 2(1892–1893): 215–249.
  33. ^ 톈위조 퀀텀 필드 이론 개념 기반 케임브리지 대학 출판 페이지 154-155
  34. ^ Gouyet, Jean-François (1996). Physics and fractal structures. Paris/New York: Masson Springer. ISBN 978-0-387-94153-0.

외부 링크