나선 목록

이 목록은 불완전하므로 누락된 항목을 추가하여 도움을 줄 수 있다.(2019년 2월)

이 나선형 목록에는 수학적으로 묘사된 나선형이라는 이름이 있다.

이미지	이름	처음 설명됨	방정식	댓글
	원을 그리다		$(\displaystyle r=k}$	사소한 소용돌이
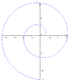
	아르키메데스 나선형	c. 기원전 320년	$\displaystyle r=a+b\cdot \theta }$
	오일러 나선형			코르누 나선형 또는 다항 나선형이라고도 한다.
	페르마의 나선형(포물선 나선형)	1636[1]	${\displaystyle r^{2}=a^{2}\theta }$
	쌍곡선 나선형	1704	$r=a/\theta }$	또한 상호 나선형
	리투우스	1722	${\displaystyle r^{2}\theta =k}$
	로그 나선형	1638[2]	${\displaystyle r=a\cdot e^{b\theta}}}$	이것의 근사치는 자연에서 발견된다.
	피보나치 나선형		피보나치 타일링에서 정사각형의 반대쪽 모서리를 연결하는 원형 호	황금 나선형의 근사치
	황금 나선형		${\displaystyle r=\varphi ^{\frac {2\theta}{\\pi }\,}$	대수 나선형의 특별한 경우
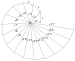
	테오도로스의 나선형(피타고라스의 나선형)			아르키메데스 나선형에 근접한, 연속적인 우측 삼각형으로 구성된 다각형 나선형 나선형
	본의 아닌	1673
	나선형의		${\displaystyle r(t)=1,\,}$ $\displaystyle \theta(t)=t=t,\,}$ $[\displaystyle h(t)=t.\,}$	입체 나선형
	룸 라인(록소드롬도 포함)			구체에 그려진 나선형의 유형
	코테스 나선	1722
	푸인소트의 나선형		${\displaystyle r=a\cschname {csch}(n\theta ),\,}$ ${\displaystyle r=a\bename {sech}(n\theta )}$
	닐슨의 나선형	1993[3]	${\displaystyle x(t)=\displayname {ci}(t),\,}$ ${\displaystyle y(t)=\displayname {si}(t)}$	사인 적분 및 코사인 적분법을 사용한 오일러 완화곡선의 변화
	다각형 나선형			로그 완화곡선의 특수 사례 근사치
	프레이저의 나선형	1908		나선형 기반 착시현상
	콘코스바이러스		${\displaystyle {\displaysty}r=\mu ^{t}a\\\\teta =t\z=\mu ^{t}c\end{case}}}}}$	원뿔 표면의 3차원 나선형
	칼킨-윌프 나선
	울람 완화곡선(일차 완화곡선)	1963
	자루의 나선형	1994		울람 나선형과 아르키메데스 나선형의 변종
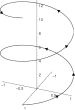
	세이퍼트의 나선형			구면의 나선 곡선
	트랙트릭스 나선형	1704[4]	${\displaystyle {\display}r=A\cos(t)\\\theta =\tan(t)-t\end{case}}$
	파푸스 나선형	1779	${\displaystyle {\case}r=a\theta \\\\data=k\end{case}}}$	Papus와 Pascal이[5] 연구한 3D 원뿔 나선형
	도플러 나선형		${\displaystyle {\case}x=a(t\cos(t)+kt)\\y=at\sin(t)\end{case}}}$	파푸스 나선형의[6] 2D 투영
	아쯔마 나선형		${\displaystyle {\case}x=\sin(t)/t-2\cosin(t)\y=-\cosin(t)/t-2\sin(t)+cos(t)\cos(t)\case}}}}}$	동그라미를 형성하는 카타코스트가 있는 곡선. 아르키메데스 나선형에 [7]가깝지
	원자 나선형	2002	$(\displaystyle r=\theta /(\theta -a)}$	이 완화곡선에는 두 개의 점증상이 있는데 하나는 반지름 1의 원이고 다른 ${\displaystyle \mathrm{하나}}$는 선 $line{\displaystyle }$= ${\displaystyle \theta =a}$이다.
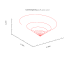
	은하 나선형	2019	${\displaystyle {\begin}dx=R*{\frac {y}{\sqrt {x^{2}+y^{2}}}}d\theta \\dy=R*{\Bigl [}\rho (\theta )-{\frac {x}{\sqrt{x^{2}+y^{2}{2}}}}{{\Bigr ]}d\theta \end{case}{\begin}x=\sum dx\\\\y=\sum dy+R\end{case}}}}}}$	차등 나선 방정식, 세개의 다른 경우:ρ<>1, ρ=1,ρ 1{\displaystyle \rho<>1,\rho=1,\rho 1},로도 나선형 패턴이 변수 ρ{\displaystyle \rho}의 행동에 결정된 4해결책을 가지고 있어 디스크의 은하가 나선 팔을 모의 실험한다.ρ<>;1{\displays 개발되었다.tyle \rho<1}, $나선{\displaystyle }$ 고리 패턴; ;${\displaystyle }$= ${\displaystyle 1}$,${\displaystyle \rho =1,}$일반 나선형$$; > 1,${\displaystyle \rho >1,}$ 느슨한 나선형. R은 중심까지의 나선 시작점(0, R)의 거리다. 계산된 x와 y는 플롯을 위해 ( -${\displaystyle \theta }$ ${\displaystyle -\theta }$)로 역회전해야 한다. 자세한[9] 내용은 참조를 참조하십시오.

참고 항목

• 캐서린 휠(불꽃 작업)
• 나선 은하 목록
• 파커 나선형
• 나선형
• 스피로그래프

참조