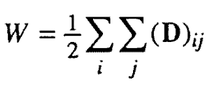거리 행렬

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : '거리 매트릭스'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2017년 2월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

수학, 컴퓨터 과학, 특히 그래프 이론에서 거리 행렬은 ^[1]집합의 요소들 사이의 거리를 쌍으로 갖는 정사각형 행렬이다.관련된 애플리케이션에 따라서는 이 매트릭스를 정의하기 위해 사용되는 거리가 메트릭이 될 수도 있고 아닐 수도 있습니다.N개의 요소가 있는 경우 이 행렬의 크기는 N×N입니다.그래프 이론 어플리케이션에서 요소는 포인트, 노드 또는 정점으로 더 자주 언급됩니다.

비메트릭 거리 행렬

일반적으로 거리 행렬은 일부 그래프의 가중 인접 행렬입니다.네트워크에서는 아크에 가중치를 할당한 방향 그래프로서 네트워크의 2노드간 거리는 ^[2]2노드를 결합하는 최단 경로상의 가중치 합계의 최소값으로 정의할 수 있다.이 거리 함수는 잘 정의되어 있지만 메트릭이 아닙니다.체중을 조합하고 비교할 수 있는 것 외에 체중에 제한이 있을 필요가 없기 때문에 일부 애플리케이션에서 음의 체중을 사용한다.경로가 지향적이기 때문에 대칭성을 보장할 수 없으며, 사이클이 존재하는 경우 거리 행렬이 비어 있지 않을 수 있습니다.

위의 대수식은 min-plus 대수를 사용하여 얻을 수 있다.이 시스템의 행렬 곱셈은 다음과 같이 정의된다: 두 n × n 행렬 A = (a_ij) 및 B = (b_ij)가 주어졌을 때, 그들의 거리곱 C = (c_ij) = A µ B는 다음과 같이 n × n 행렬로 정의된다.

${\displaystyle c_{ij}=\min _{k=1}^{n}\{a_{ik}+b_{kj}\}.}$

min-plus 연산이 올바르게 작동하려면 직접 연결되지 않은 대각선 요소를 무한대 또는 적절한 큰 값으로 설정해야 합니다.이러한 위치에 0이 있으면 거리나 비용 등이 없는 가장자리로 잘못 해석됩니다.

W가 그래프의 가장자리 가중치를 포함하는 n × n 행렬인 경우^k, (이 거리 곱을 사용하여) W는 최대 k개의 가장자리 길이의 경로를 사용하여 정점 사이의 거리를 제공하고ⁿ, W는 그래프의 거리 행렬이다.

n개의 정점에 대한 임의의 그래프 G는 G의 엣지에 대응하는 완전 그래프의 각 엣지에 1의 가중치를 할당하고 다른 모든 엣지에 0의 가중치를 할당함으로써 n개의 정점에 대한 가중치 완전 그래프로 모델링할 수 있다.이 완전한 그래프의 W는 G의 인접 매트릭스입니다.G의 거리 행렬은 위와 같이 W에서 계산할 수 있지만, 일반적인ⁿ 행렬 곱셈으로 계산되는 W는 길이가 정확히 n인 두 꼭지점 사이의 경로 수만 인코딩합니다.

미터법 거리 행렬

많은 응용 프로그램에서 거리 행렬 형식주의의 가치는 거리 행렬이 메트릭 공리를 명확하게 부호화할 수 있는 방법과 선형 대수 기법의 사용에 어떻게 도움이 되는지에 있다.즉, M = (x_ij)가 1µi인 경우, j µN은 미터법의 거리에 대한 거리 행렬이다.

1. 주 대각선의 엔트리는 모두 0이다(즉, 행렬은 중공 매트릭스이다). 즉, 모든_ii 1 µ i µ N에 대해 x = 0이다.
2. 오프캐릭 엔트리는 모두 양수(i_ij µj의 경우 x > 0), 즉 음수가 아닌 매트릭스),
3. 행렬은 대칭 행렬(x_ij = x_ji)입니다.
4. 임의의 i와 j에 대해 모든 k에 대해 x µ_ik x + x_kj(삼각형 부등식)입니다_ij.이것은 열대 행렬 곱셈의 관점에서 언급될 수 있다.

거리 행렬이 처음 세 개의 공리를 만족하는 경우(반 메트릭으로 함) 프리-디스턴스 행렬이라고도 합니다.유클리드 공간에 포함될 수 있는 전거리 행렬을 유클리드 거리 행렬이라고 합니다.

부호화 이론에서 미터법 거리 행렬의 또 다른 일반적인 예는 블록 코드에서 요소가 알파벳 위에 고정된 길이의 문자열이고 이들 사이의 거리가 해밍 거리 메트릭에 의해 주어질 때 발생한다.거리 행렬에서 0이 아닌 최소 항목은 코드의 오류 수정 및 오류 탐지 기능을 측정합니다.

가법 거리 행렬

가법거리행렬은 생물정보학에서 계통발생학적 트리를 구축하기 위해 사용되는 특별한 종류의 매트릭스이다.x가 두 종 i와 j 사이의 가장 낮은 공통 조상이라고 가정하면, M = M + M이_xj 예상됩니다_ijix.이것이 가법 메트릭의 근원입니다.한 쌍의 종 S에 대한 거리행렬 M은 다음과 같이 S에 대한 계통발생 T가 존재하는 경우에만 가법이라고 한다.

• T의 모든 에지(u,v)는 양의 무게_uv d와 관련지어집니다.
• 모든 i,j † S에 대해_ij M은 T의 i에서 j까지의 경로를 따라 가중치의 합계와 같다.

이 경우 M을 가법 행렬이라고 하고 T를 가법 나무라고 합니다.아래에서는 가법 거리 행렬과 이에 대응하는 트리의 예를 볼 수 있습니다.

울트라메트릭 거리 매트릭스

초측정 거리 행렬은 일정한 분자 시계를 모델링하는 가법 행렬로 정의됩니다.그것은 계통수를 만드는 데 사용된다.매트릭스 M은 다음과 같은 트리 T가 존재하는 경우 초메트릭이라고 한다.

• M은_ij T에서 i에서 j까지의 경로를 따라 에지 가중치의 합계와 같습니다.
• 나무의 뿌리는 모든 잎과의 거리가 같은 것으로 식별할 수 있다.

다음은 대응하는 트리와 함께 울트라메트릭 거리 매트릭스의 예입니다.

생물정보학

거리 행렬은 생물 정보학 분야에서 널리 사용되며, 여러 방법, 알고리즘 및 프로그램에 존재한다.거리행렬은 배열공간에서 두 배열 사이의 쌍방향 거리뿐만 아니라 좌표와 무관한 방식으로 단백질 구조를 나타내기 위해 사용된다.구조 및 순차 정렬 및 NMR 또는 X선 결정학에서 단백질 구조를 결정하는 데 사용됩니다.

데이터를 유사도 행렬로 표현하는 것이 더 편리할 수 있습니다.

거리 상관 관계를 정의하는 데도 사용됩니다.

시퀀스 얼라인먼트

두 시퀀스의 정렬은 두 시퀀스의 길이가 같고 두 개의 증강된 ^[3]시퀀스의 같은 위치에 두 개의 공간이 없도록 시퀀스를 따라 임의의 위치에 공간을 삽입함으로써 형성된다.시퀀스 정렬의 주요 방법 중 하나는 동적 프로그래밍입니다.이 방법은 거리 행렬을 채운 다음 선형을 얻는 데 사용됩니다.일반적으로 배열 정렬을 위해 매트릭스를 사용하여 아미노산 일치 또는 불일치에 점수를 할당하고 아미노산과 다른 배열의 갭을 일치시키는 갭 패널티를 부여한다.

글로벌 얼라인먼트

전역 정렬 계산에 사용되는 Needleman-Wunsch 알고리즘은 동적 프로그래밍을 사용하여 거리 행렬을 얻습니다.

로컬 얼라인먼트

Smith-Waterman 알고리즘은 또한 거리 행렬을 얻은 다음 로컬 정렬을 얻는 동적 프로그래밍 기반입니다.

다중 시퀀스 얼라인먼트

다중 시퀀스 정렬은 한 번에 여러 시퀀스를 정렬하기 위한 쌍별 정렬의 확장입니다.다른 MSA 방법은 전역 및 로컬 정렬과 동일한 거리 매트릭스 아이디어를 기반으로 합니다.

• 중심별 방식.이 방법은 시퀀스_c S와 다른 시퀀스_i S 사이의 거리를 최소화하는 중심 시퀀스_c S를 정의합니다.그런 다음 시퀀스 세트 S에 대해 다중 정렬 M을 생성하여 모든_i S에 대해 정렬 거리_M d(S_c,S_i)가 최적의 쌍방향 정렬이 되도록 합니다.이 방법은 쌍화 거리가 최적 다중 정렬의 최대 두 배인 S에 대해 계산된 정렬의 특성을 가집니다.
• 프로그레시브 얼라인먼트 방식.MSA를 작성하는 이 경험적 방법은 가장 관련성이 높은 두 시퀀스를 먼저 정렬하고 모든 시퀀스가 정렬될 때까지 다음 두 시퀀스를 순차적으로 정렬합니다.

그 인기에 따라 독자적인 프로그램이 있는 다른 방법도 있습니다.

• 클러스터
• 근육
• 마후토
• 망고
• 그 밖에도

마후토

고속 푸리에 변환(MAFFT)을 이용한 다중 얼라인먼트는 프로그레시브 얼라인먼트에 기반한 알고리즘으로 다양한 다중 얼라인먼트 전략을 제공합니다.첫째, MAFFT는 공유된 6개의 튜플 수를 기반으로 거리 행렬을 구성합니다.둘째, 이전 매트릭스를 기반으로 가이드 트리를 구축합니다.셋째, Fast Fourier Transform의 도움을 받아 시퀀스를 클러스터링하고 정렬을 시작합니다.새 정렬을 기반으로 가이드 트리를 재구성하고 다시 정렬합니다.

계통학적 분석

계통발생학적 분석을 수행하기 위해, 첫 번째 단계는 계통수를 재구성하는 것이다: 종의 집합이 주어졌을 때, 문제는 종 사이의 조상 관계, 즉 종 사이의 계통수를 재구성하거나 추론하는 것이다.이 액티비티는 거리 매트릭스 메서드에 의해 실행됩니다.

거리 행렬법

계통발생학적 분석의 거리 매트릭스 방법은 분류되는 배열 사이의 "유전자적 거리" 측정에 명시적으로 의존하며, 따라서 입력으로서 여러 개의 배열이 필요하다.거리 방법은 각 시퀀스 쌍 간의 거리를 설명하는 시퀀스 쿼리 집합에서 전체 매트릭스를 구성하려고 시도합니다.이를 통해 동일한 내부 노드 아래에 밀접하게 관련된 염기서열을 배치하고 분기 길이가 염기서열 사이의 관측된 거리를 밀접하게 재현하는 계통 발생 트리를 구성한다.거리 매트릭스 방법은 ^[4]루트 트리를 계산하는 데 사용된 알고리즘에 따라 루트 트리 또는 비루트 트리를 생성할 수 있다.n종이 주어졌을 때 입력은 n x n 거리 행렬 M입니다.여기서_ij M은 i종과 j종 사이의 돌연변이 거리입니다.목표는 거리 행렬과 일치하는 3등급의 트리를 출력하는 것입니다.

다중 시퀀스 정렬의 프로그레시브 및 반복 유형의 기준으로 자주 사용됩니다.거리 매트릭스 방법의 주요 단점은 여러 하위 ^[4]트리에 걸쳐 나타나는 국소 고변동 영역에 대한 정보를 효율적으로 사용할 수 없다는 것이다.잠재적인 문제에도 불구하고 거리 방법은 매우 빠르고 종종 계통 발생의 합리적인 추정치를 산출한다.또한 문자를 직접 사용하는 방법보다 몇 가지 이점이 있습니다.특히 거리 방법은 DNA-DNA 교배 분석과 같이 문자 데이터로 쉽게 변환되지 않는 데이터를 사용할 수 있도록 한다.

다음은 계통 재건을 위한 거리 기반 방법입니다.

• 가법 트리 재구성
• 업그마
• 네이버 가입
• 피치마골리아시

가법 트리 재구성

가법 트리 재구성은 가법 및 초측정 거리 행렬을 기반으로 합니다.이들 매트릭스에는 다음과 같은 특별한 특징이 있습니다.

가법 행렬 M을 고려합니다.모든 3종 i, j, k에 대해 대응하는 나무는 유일하다.^[3]모든 울트라메트릭 거리행렬은 가법행렬이다.우리는 이 특성을 i, j, k의 종으로 구성된 아래의 나무에 대해 관찰할 수 있다.

추가 트리 재구성 기술은 이 트리에서 시작됩니다.그리고 위에서 언급한 특성과 결합된 거리 행렬에 따라 매번 한 종을 추가합니다.예를 들어 가법행렬 M과 5종 a, b, c, d, e를 고려한다면.먼저 우리는 두 종의 a와 b를 위한 첨가 나무를 형성한다.그리고 세 번째 것을 골랐습니다.예를 들어 c라고 하고 a와 b 사이의 끝점 x에 붙입니다.가장자리 가중치는 위의 속성을 사용하여 계산됩니다.다음으로 네 번째 종 d를 가장자리 중 하나에 추가합니다.속성을 적용하면 d는 특정 엣지 1개에만 부착해야 합니다.마지막으로 이전과 동일한 절차에 따라 e를 추가합니다.

업그마

UPGMA(Unweighted Pair Group Method with 산술평균법)의 기본원칙은 계통수에서 유사한 종이 더 가까이 있어야 한다는 것이다.따라서 유사한 시퀀스를 반복적으로 클러스터링하여 트리를 구축합니다.이 방법은 잎에서 아래로 내려오는 계통수를 만드는 것이다.처음에는 잎이 n개(또는 싱글톤 나무 n개)로 각각 S의 종을 나타냅니다.이러한 n개의 리프는 n개의 클러스터라고 불립니다.그런 다음 n-1번의 반복을 수행합니다.각 반복에서 평균 거리가 가장 작은 2개의 클러스터₁ C와₂ C를 식별하고 이들을 병합하여 더 큰 클러스터 C를 형성합니다.UPGMA 알고리즘에 의해 작성된 클러스터 C에 대해 M이 울트라메트릭이라고 가정하면 C는 유효한 울트라메트릭트리입니다

네이버 가입

네이버는 상향 클러스터링 방식입니다.각 시퀀스 쌍 사이의 거리를 지정하는 거리 행렬을 사용합니다.이 알고리즘은 스타 네트워크의 토폴로지에 대응하는 완전히 해결되지 않은 트리에서 시작하여 트리가 완전히 해결되어 모든 브랜치 길이를 알 수 있을 때까지 다음 단계를 반복합니다.

1. 현재 거리 행렬을 기반으로 행렬을 계산합니다(아래 정의).
2. 값이 가장 낮은 고유 분류 i와 j(즉, 와) 쌍을 찾습니다.이러한 분류는 중앙 노드에 연결된 새로 생성된 노드에 결합됩니다.오른쪽 그림에서는 f와 g가 새로운 노드 u에 결합되어 있다.
3. 쌍의 각 분류군으로부터 이 새로운 노드까지의 거리를 계산합니다.
4. 이 쌍의 바깥쪽에 있는 각 분류군으로부터 새로운 노드까지의 거리를 계산합니다.
5. 알고리즘을 재기동하여 가입된 네이버 쌍을 새 노드로 교체하고 이전 ^[5]단계에서 계산된 거리를 사용합니다.

피치마골리아시

Fitch-Margoliash 방법은 유전적 거리에 기초한 군집화를 위해 가중 최소 제곱 방법을 사용합니다.원거리 관련 시퀀스 간 거리 측정의 부정확성 증가를 수정하기 위해 트리 구축 프로세스에서 밀접하게 관련된 시퀀스에 더 많은 가중치가 부여된다.이러한 거리에 적용되는 최소 제곱 기준은 인접 결합 방식보다 정확하지만 효율은 낮습니다.데이터 집합의 많은 밀접하게 관련된 시퀀스로부터 발생하는 거리 사이의 상관관계를 수정하는 추가 개선도 증가된 계산 ^[6]비용으로 적용할 수 있다.

데이터 마이닝 및 머신 러닝

데이터 마이닝

데이터 마이닝의 일반적인 기능은 주어진 데이터 세트에 대해 클러스터 분석을 다른 그룹과 비교할 때 얼마나 비슷하거나 더 유사한지에 따라 그룹 데이터에 적용하는 것입니다.거리 매트릭스는 거리 메트릭을 사용하여 유사성을 측정할 수 있기 때문에 클러스터 분석에 크게 의존하게 되고 활용됩니다.따라서, 거리 행렬은 집합 내의 모든 다른 데이터 쌍들 사이의 유사성 측정의 표현이 되었다.

계층 클러스터링

거리 행렬은 종종 계통재건과 같은 생물과학에서 사용되는 발견적 방법인 전통적인 계층적 클러스터링 알고리즘에 필요하다.데이터 마이닝에서 계층적 클러스터링 알고리즘을 구현할 때 거리 매트릭스는 모든 점 사이의 모든 쌍별 거리를 포함하며, 그 후 거리 매트릭스로부터의 거리를 기반으로 두 개의 다른 점 또는 클러스터 간에 클러스터를 생성하기 시작합니다.

여기서 N은 점의 수이고 계층 군집화는 다음과 같습니다.

• 거리 행렬을 업데이트하기 위해 모든 클러스터 이후에 수행된 반복 계산으로 인해 시간 복잡도는 O(N^3)입니다.
• 공간의 복잡도는 O(N^2)

기계 학습

거리 측정 기준은 여러 기계 학습 알고리즘의 핵심 부분으로, 지도 학습과 비지도 학습 모두에 사용된다.일반적으로 데이터 점 간의 유사도를 계산하는 데 사용됩니다. 거리 행렬이 필수 요소입니다.효과적인 거리 행렬을 사용하면 분류 작업용이든 ^[7]클러스터링용이든 기계 학습 모델의 성능이 향상됩니다.

K-Nearest 네이버

거리 행렬은 분류 태스크와 회귀 태스크 모두에서 사용할 수 있는 가장 느리지만 단순하며 가장 많이 사용되는 인스턴스 기반 기계 학습 알고리즘 중 하나인 k-NN 알고리즘에서 사용됩니다.각 테스트 샘플의 예측 결과에는 테스트 샘플과 훈련 세트의 각 훈련 샘플 사이에 완전히 계산된 거리 행렬이 필요하기 때문에 가장 느린 기계 학습 알고리즘 중 하나입니다.거리 행렬이 계산되면 알고리즘은 세트의 다수(분류) 또는 평균(회귀) 값을 기반으로 테스트 표본의 결과를 예측하기 위해 검정 표본에 가장 가까운 K개의 교육 표본 수를 선택합니다.

• 예측 시간 복잡도 O(k * n * d) - 거리 행렬을 구성하기 위해 각 검정 표본과 모든 교육 표본 사이의 거리를 계산합니다.

1. k = 선택된 가장 가까운 네이버 수
2. n = 교육 세트의 크기
3. d = 데이터에 사용되는 차원 수

이 분류 중심 모형은 목표값과 각 교육 표본 사이의 거리 행렬을 기반으로 목표값의 레이블을 예측하여 목표값에 가장 가깝거나 가까운 표본의 K 번호를 결정합니다.

컴퓨터 비전

Neural Networks에서 영상 예측 기계 학습 모델에서 2D-3D 회귀를 위해 거리 매트릭스를 사용할 수 있습니다.

정보 검색

가우스 혼합 거리를 사용한 거리 관계

• [1]* 정보 검색을 위해 정확한 가장 가까운 이웃 검색을 수행하기 위한 가우스 혼합 거리.데이터베이스 내의 데이터 분포를 위한 확립된 가우스 유한혼합모델 하에서 가우스혼합거리는 검색 데이터의 분포와 데이터베이스 내의 데이터 간의 쿨백-라이블러 차이를 최소화하는 것에 기초해 공식화된다.정밀 성능 측정을 바탕으로 잘 알려진 유클리드 및 마할라노비스 거리와 가우스 혼합 거리의 성능 비교.실험 결과는 가우스 혼합 거리 함수가 다른 유형의 테스트 데이터에 대해 다른 함수보다 우수하다는 것을 보여준다.

정보 재수술을 주제로 주목할 만한 잠재적 기본 알고리즘은 Fish School Search 알고리즘으로, 어학원의 집단 행동을 수집하기 위해 거리 입학을 사용하는 행위에 참여하는 정보 재수법이다.공급 오퍼레이터를 사용하여 체중 업데이트

질문 A:

${\displaystyle x_{i}(t+1)=x_{i}(t)-{vol}rand(0,1){\frac {x_{i}(t)-B(t)}{distance(x_{i}(t)}},$

질문 B:

${\displaystyle x_{i}(t+1)=x_{i}(t)+step_{vol}rand(0,1){\frac {x_{i}(t)-B(t)}{distance(x_{i}(t)}}},$

Stepvol은 거리 매트릭스로 사전 형성된 최대 볼륨 변위의 크기를 정의합니다.특히 유클리드 거리 행렬 사용

코사인 직유사성 및 거리대수의 유사성 또는 차이성 평가

• [2]* 코사인 유사도 측정은 코사인 베이스의 서치 공간에서 문서 간의 각도를 측정하여 정보 검색에서 가장 자주 적용되는 근접도 측정일 수 있습니다.유클리드 거리는 평균 보정에 불변한다.평균의 표본분포는 동일한 모집단에서 반복적으로 표본을 추출하여 얻은 표본수단을 기록함으로써 생성된다.이 분포는 서로 다른 평균의 분포를 형성하며, 이 분포에는 고유한 평균과 분산이 있습니다.양수뿐만 아니라 음수일 수 있는 데이터의 경우 코사인 유사성에 대한 null 분포는 두 개의 독립적인 랜덤 단위 벡터의 닷 곱의 분포입니다.이 분포의 평균은 0이고 분산은 1/n입니다.반면 유클리드 거리는 이 보정에 불변할 것이다.

클러스터화 문서

유사한 문서를 정리하고 그룹화하기 위해 거리 기반 메트릭을 사용한 계층적 클러스터링을 구현하려면 거리 매트릭스의 필요성과 활용이 필요합니다.거리 행렬은 사용자의 질의를 위해 관련 문서의 검색 방법에 사용되는 밀접하게 연관된 문서의 클러스터를 만드는 데 사용되는 다른 문서와 문서가 가지는 연관성을 나타냅니다.

ISOMAP

Isomap은 거리 행렬을 통합하여 지오데식 거리를 활용하여 저차원 임베딩을 계산할 수 있습니다.이를 통해 방대한 수의 차원에 존재하는 문서 모음에 대처하고 문서 클러스터링을 수행할 수 있습니다.

네이버 검색 비주얼라이저(NeRV)

디스플레이/화면에 표시된 유사성을 기반으로 유사한 데이터를 찾기 위해 거리 행렬을 사용하는 비감독 및 감독 시각화에 모두 사용되는 알고리즘입니다.

비지도 NeRV에 필요한 거리 행렬은 고정 입력 쌍별 거리를 통해 계산할 수 있다.

감독된 NeRV에 필요한 거리 매트릭스는 감독된 방식으로 입력의 거리를 계산할 수 있도록 감독된 거리 메트릭을 공식화해야 한다.

화학

거리 행렬은 ^[8]화학의 그래픽-이론(토폴로지) 및 기하학(토폴로지) 버전 모두에서 널리 사용되는 수학적 객체입니다.거리 행렬은 화학에서 명시적 형식과 암묵적 형식 모두에서 사용됩니다.

2개의 치환 이성질체 간의 상호 변환 메커니즘

거리 행렬은 두 치환 이성질체 사이의 재배열을 결정하는 데 필요한 최단 경로 시퀀스를 묘사하고 밝히는 주요 접근법으로 사용되었다.

거리 다항식 및 거리 스펙트럼

분자 구조의 거리 다항식과 거리 스펙트럼을 구성하기 위해서는 거리 행렬의 명시적 사용이 필요하다.

구조 속성 모델

거리 행렬의 암묵적 사용은 모든 화학 구조에서 거리를 나타내기 위해 공식화된 거리 기반 메트릭 와이너 번호/와이너 지수의 사용을 통해 적용되었다.와이너 수는 거리 행렬 요소의 반합과 같습니다.

그래프 이론 거리 행렬

분자 그래프의 2-D 실현에 사용되는 화학의 거리 매트릭스로, 무수한 응용 분야에서 분자의 주요 기본 특징을 설명하는 데 사용됩니다.

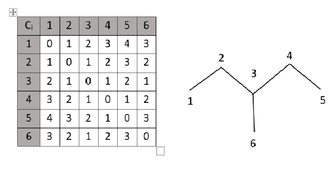
1. 거리 매트릭스를 기반으로 분자의 탄소 골격을 나타내는 라벨 트리를 만듭니다.유사한 분자가 탄소 골격의 무수한 라벨 트리 변형을 가질 수 있기 때문에 거리 행렬은 이 응용 분야에서 필수적입니다.이 예에서 거리 매트릭스를 기반으로 생성된 헥산₆₁₄(CH) 탄소 골격의 라벨 트리 구조는 거리 매트릭스와 라벨 트리 모두에 영향을 미치는 다른 탄소 골격 변형을 가집니다.
2. 화학 그래프 이론에서 사용되는 모서리 무게를 가진 레이블이 있는 그래프를 만듭니다. 이 그래프는 이질 원자가 있는 분자를 나타냅니다.
3. Le Verrier-Fadeev-Frame(LVFF) 방법은 다환 그래프에서 그래프 중심을 검출하는 프로세스의 속도를 높이기 위해 사용되는 컴퓨터 지향 방법입니다.단, LVFF에서는 입력이 대각선화된 거리행렬이어야 하며, LVFF 방법에 필요한 대각선화된 거리를 반환하는 Houdeer 삼각선-QL 알고리즘을 구현하면 쉽게 해결할 수 있습니다.

기하학적 거리 행렬

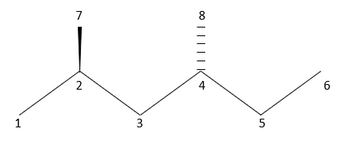
그래프 이론 거리 행렬 2-D는 분자의 구성 특징을 포착하는 한편, 그 3차원(3D) 특성은 기하학적 거리 행렬에 부호화된다.기하학적 거리 행렬은 3차원 분자 ^[8]구조를 나타내고 그래프로 나타내기 위해 분자의 그래프 이론 거리 행렬에 기초한 다른 유형의 거리 행렬입니다.분자 구조 G의 기하학적 거리 행렬은 2-D 행렬과 같은 방식으로 정의된 실제 대칭 n x n 행렬입니다.그러나 매트릭스_ij 요소 D는 G에서 i와 j 사이의 최단 데카르트 거리 컬렉션을 유지합니다.지형 매트릭스로도 알려진 기하학적 거리 매트릭스는 분자의 알려진 기하학적 구조로부터 구성될 수 있습니다.예를 들어, 2,4-디메틸헥산의 탄소 골격의 기하학적 거리 매트릭스는 다음과 같습니다.

기타 응용 프로그램

시계열 분석

동적 시간 뒤틀림 거리 행렬은 시계열 객체의 집합/그룹의 클러스터링 및 분류 알고리즘과 함께 이용된다.

예

예를 들어, 픽셀 유클리드 거리가 거리 메트릭인 이러한 데이터를 분석한다고 가정합니다.

거리 행렬은 다음과 같습니다.

	a	b	c	d	e	f
a	0	184	222	177	216	231
b	184	0	45	123	128	200
c	222	45	0	129	121	203
d	177	123	129	0	46	83
e	216	128	121	46	0	83
f	231	200	203	83	83	0

그런 다음 이러한 데이터를 그래픽 형태로 열 지도로 볼 수 있습니다.이 이미지에서 검은색은 0의 거리를 나타내고 흰색은 최대 거리를 나타냅니다.

「 」를 참조해 주세요.

• 컴퓨터 비전
• 중공 행렬
• 데이터 클러스터링
• 최소 행렬 곱셈

레퍼런스