원뿔 단면의 행렬 표현

수학에서 원뿔단위의 행렬표현은 원뿔단면 연구에 선형대수의 도구를 사용할 수 있게 한다. 원뿔 단면의 축, 정점, 접선, 원뿔에 의해 결정되는 평면의 점과 선 사이의 극과 극 관계를 쉽게 계산할 수 있는 방법을 제공한다. 이 기법은 원뿔 단면의 방정식을 표준 형식에 넣을 필요가 없으므로, 축이 좌표계에 평행하지 않은 원뿔 단면을 더 쉽게 조사할 수 있다.

원뿔 단면(후진 단면 포함)은 좌표가 두 변수에서 2차 다항 방정식을 만족하는 점 집합이다.

[\displaystyle Q(x,y)=Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0.}

표기법의 남용으로 이 원뿔 부분은 혼동이 일어날 수 없을 $때$ Q라고도 불릴 것이다.

이 방정식은 다음과 같이^[1] 일부 후속 공식을 단순화하기 위해 대칭 행렬의 관점에서 행렬 표기법으로 작성할 수 있다.

\left({\begin{matrix}x&y\end{matrix}}\right)\left({\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right)\left({\begin{matrix}x\\y\end{matrix}}\right)+\left({\begin{matrix}D&E\end{matrix}\오른쪽)\왼쪽({\begin{matrix}x\\y\end{matrix}\오른쪽)+F=0.

이 방정식의 처음 세 항의 합, 즉

Ax^{2}+Bxy+Cy^{2}=\왼쪽({\begin{matrix}x&y\end{matrix}\오른쪽)\왼쪽({\begin{matrix}A&B/2\\b/2&C\end{matrix}\오른쪽)\왼쪽({\begin}x\y\end{matrix}}}오른쪽),

등식 및 행렬과 관련된 2차 형태

A_{33}=\왼쪽({\begin{matrix}A&B/2\\B/2&C\end{matrix}\오른쪽)

2차 형태의 행렬이라고 불린다. A $A_{33}$ ${\$ 의 추적과 결정요소는 축의 회전과 평면(원점 이동)에 있어 모두 불변이다.^[2]^[3]

2차 방정식은 또한 다음과 같이 쓸 수 있다.

\mathbf {x} ^{T}A_{Q}\mathbf {x} =0,

여기서 $\mathbf {x}$ ${\$ 은(는) 마지막 변수가 1이 되도록 제한된 세 변수의 균일한 좌표 벡터다 $\mathbf {x}$ .

{\pmatrix}x\\y\1\end{pmatrix}}

그리고 $A_{Q}$ 서 $A_{Q}$ Q $A_{Q}$ {\ $displaystyle A_{Q}}$ 는 $A_{Q}$ 행렬이다.

A_{Q}={\begin{pmatrix}A&B/2&D/2\\B/2&C&E/2&F\end{pmatrix}.

행렬 $A_{Q}$ $A_{Q}$ ${\$ 를 이차 방정식의 행렬이라고 한다 $A_{Q}$ .^[4] A ${\$ 의 그것과 마찬가지로 $A_{33}$ 그것의 결정요소는 회전과 번역 모두에 대하여 불변한다.^[3]

A에서 $Q$ 세 번째(마지막) 행과 세 번째(마지막) 열을 제거하여 얻은 $A$ 의_Q 2×2 왼쪽 상단 서브매트릭스(순서 2의 행렬)는 2차 형태의 매트릭스는 A에서 세 번째(마지막) 열과 세 번째(마지막) 열을 제거하여 얻은 것이다. 위의 $표기법 33$ A는 이 관계를 강조하기 위해 이 글에서 사용된다.

분류

$A$ 의_Q 결정요인에 따라 적절한(비감소) 및 퇴화된 원뿔 단면을 구별할^[5]^[6] 수 있다.

$\det A_{Q}=0$ $\det A_{Q}=0$ $\det A_{Q}=0$ = $\det A_{Q}=0$ ${\displaystyle \det A_{Q}=0$ 인 경우 원뿔은 변질된다.

$Q$ 가 변질되지 않도록 $\det A_{Q}\neq 0$ $\det A_{Q}\neq 0$ A $\det A_{Q}\neq 0$ $≠$ $\det A_{Q}\neq 0$ $\det A_{Q}\neq 0$ detect A \ $det A_{33$ :

$Q$ 는 $\det A_{33}<0$ A $\det A_{33}<0$ < $\det A_{33}<0$ $\det A_{0$ 인 $경우$ 에만 하이퍼볼라다 $\det A_{33}<0$
$Q$ 는 $\det A_{33}=0$ $\det A_{33}=0$ $\det A_{33}=0$ = $\det A_{33}=0$ ${\displaystyle \det A_{33}=0$ 인 경우에만 포물선이다.
$Q$ 는 $\det A_{33}>0$ A $\det A_{33}>0$ > 0 ${\displaystyle \det$ A_ ${33$ }> $0}$ 인 경우에만 타원이다 $\det A_{33}>0$

타원의 경우 $x$ 와² $y$ 의² 계수에 해당하는 마지막 두 대각선 원소를 비교하여 원의 특별한 경우를 구별할 수 있다.

$A$ = $C$ , $B$ = $0$ 이면 $Q$ 는 원이다.

AQ<>det 만약(A+C)또한,non-degenerate 타원(로 det 33>0{\displaystyle\det A_{33}>0}일 경우와 det Q≠ 0{\displaystyle\det A_{Q}\neq 0})의 경우, 우리는;0}일 경우지만 상상의 타원 AQ>det(A+C);0{\displ 진정한 타원 0{\displaystyle(A+C)\det A_{Q}&lt다.aystyle(A+C)\d $et A_{Q}>0$ 후자의 예로는 x $x^{2}+y^{2}+10=0$ + $x^{2}+y^{2}+10=0$ + $x^{2}+y^{2}+10=0$ = $x^{2}+y^{2}+10=0$ {\ $displaystyle$ x $^{2}+y^{2}+10=0}$ 이 있는데 $x^{2}+y^{2}+10=0$ 이 경우 실제 값을 매기는 솔루션은 없다.

원뿔 섹션이 퇴보된 경우( $\det A_{Q}=0$ $\det A_{Q}=0$ $\det A_{Q}=0$ = $\det A_{Q}=0$ ${\displaystyle \det A_{Q}=0})$ $\det A_{33}$ A $\det A_{33}$ ${\$ 여전히 형식을 $\det A_{33}$ 구별할 수 있다.

$\det A_{33}<0$ A $\det A_{33}<0$ < 0 $\det A_{33}<0$ {\ $displaystyle \det A_{$ 33 $}<$ 0}을(를) 분리한 경우에만 두 개의 교차선(하이볼라가 두 개의 점근으로 퇴보됨 $\det A_{33}<0$
$\det A_{33}=0$ A $\det A_{33}=0$ = $\det A_{33}=0$ $\det A_{33}=0$ 인 경우에만 평행 직선 2개 $\det A_{33}=0$ 후진 포물선). These lines are distinct and real if $D^{2}+E^{2}>4(A+C)F$ , coincident if $D^{2}+E^{2}=4(A+C)F$ , and non-existent in the real plane if $D^{2}+E^{2}<4(A+C)F$ .
$\det A_{33}>0$ A $\det A_{33}>0$ > $\det A_{33}>0$ $\det A_{33}>0$ 인 경우에만 단일 점(후진 타원 $\det A_{33}>0$

동시선의 경우는 3 × 3 $A_{Q}$ A $A_{Q}$ ${\$ 의 순위가 1인 $A_{Q}$ 경우에만 발생하며, 다른 모든 퇴행의 경우 순위가 2인 경우에 발생한다.^[2]

중앙 코닉

$\det A_{33}\neq 0$ A $\det A_{33}\neq 0$ $\det A_{33}\neq 0$ $\det A_{33}\neq 0$ ${\displaystyle \det A_{33}\neq$ 0 $}$ 이(가) 있을 때 원뿔 부분의 기하학적 중심이 $\det A_{33}\neq 0$ 존재하며 그러한 원뿔 부분(엘립스 및 하이퍼볼라)을 중심 원뿔이라고 한다.^[7]

중심

원뿔의 중심은 만약 존재한다면 그것을 통과하는 원뿔의 모든 화음을 이등분하는 지점이다. 이 특성은 중앙의 좌표를 계산하는 데 사용할 수 있으며, 2차 $함수$ Q의 구배가 소멸되는 지점(즉,^[8]

\nabla Q=\왼쪽[{\frac {\partial Q}{\partial x},{\partial Q}{\partial y}\right]=[0,0]

이것은 아래와 같이 중심을 산출한다.

2차 방정식의 행렬 형식을 사용하는 대안적 접근법은 중심이 좌표계의 원점일 때 방정식에 선형 항이 없다는 사실에 기초한다. $좌표$ 원점 $($ $x 0$ $,$ $y 0)$ 에 대한 모든 $변환$ 을₀ x* = x – x, y* = $y$ - $y$ 를₀ 사용하여

\left\put}x^{*}+x_{0}}&y^{*}+y_{0}\end{matrix}\오른쪽)\좌측({\begin{matrix}A&B/2\\B/2&C\end{matrix}\우측)\좌측({\begin}x^{*}+x_{0}\\y^{*}+y_{0}\end{matrix}\오른쪽)+\왼쪽({\begin{matrix}D&E\end{matrix}\오른쪽)\왼쪽({\begin{matrix}x^{*}+x_{0)}\\y^{*}+y_{0}\end{production}\오른쪽)+F=0.

$(x 0,$ $y 0)$ 가 원뿔의 중심 $(x c,$ $y c)$ 이 되는 조건은 이 $방정식$ 을 곱할 때 선형 x $*$ 와 y $*$ 항의 계수가 0이라는 것이다. 이 조건은 중심 좌표를 생성한다.

{\begin{pmatrix}x_{c}\\y_{c}\end{pmatrix}}={\begin{pmatrix}A&B/2\\B/2&C\end{pmatrix}}^{\!-1}{\begin{pmatrix}-D/2\\-E/2\end{pmatrix}}={\begin{pmatrix}(BE-2CD)/(4AC-B^{2})\\(DB-2AE)/(4AC-B^{2})\end{pmatrix}}.

또한 이 계산은 관련 행렬 $A$ 의_Q 처음 두 행을 취하여 각각 ( $x,$ $y, ⊤$ 1)씩 곱하고 두 내부 제품을 모두 0으로 설정하여 다음과 같은 시스템을 얻을 수 있다.

Ax+(B/2)y+D/2=0,

(B/2)x+Cy+E/2=0.

이것은 위의 중심점을 산출한다.

포물선의 경우, 즉 $4AC 2$ - B = $0일$ 때, 위의 분모가 0이 되기 때문에 중심이 없다(또는 프로젝트적으로 해석하면 중심은 무한대로 선상에 있다).

중심행렬 방정식

중심(비 파라볼라) 원뿔 A $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ + B $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ y $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ + $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ y $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ + $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ + $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ + F $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ = $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ ${\displaysty Ax^{2}+Bxy+$ $Cy^{2}+Dx+Ey$ $+F=0}$ 은(는) 다음과 같이 중심 매트릭스 형식으로 다시 작성할 수 있다 $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ .

\left({\begin{matrix}x-x_{c}&y-y_{c}\end{matrix}}\right)\left({\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right)\left({\begin{matrix}x-x_{c}\\y-y_{c}\end{matrix}}\right)=K,

어디에

K={\frac {-\det(A_{Q}})}{AC-(B/2)^{2}}={\frac {-\det(A_{Q}}}}{\det(A_{33)}}}}}}}.

Then for the ellipse case of $AC > (B /2) 2$ , the ellipse is real if the sign of $K$ equals the sign of $(A + C)$ (that is, the sign of each of $A$ and $C$ ), imaginary if they have opposite signs, and a degenerate point ellipse if $K = 0$ . In the hyperbola case of $AC < (B /2) 2$ , the hyperbola is degenerate if and only if $K = 0$ .

중심 원뿔의 표준 형태

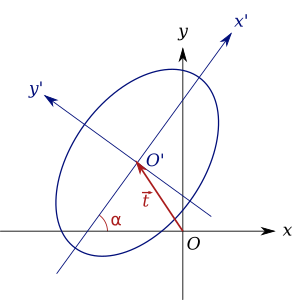
중심 원뿔 섹션의 방정식의 표준 형식은 원뿔 섹션의 중심이 좌표계의 중심에 있고 그 축이 좌표 축과 일치하도록 변환되고 회전할 때 얻는다. 이는 좌표계의 중심이 이동되고 좌표 축이 회전하여 이러한 특성을 만족시킨다고 말하는 것과 같다. 도표에서 원점 $O$ 가 있는 원래 xy 좌표계는 원점 $O$ 가 있는 $xy$ 좌표계로 이동한다 $.$

좌표 변환 및 회전

변환은 벡터 ${\vec {t}}={\begin{pmatrix}x_{c}\\y_{c}\end{pmatrix}}.$ → ${\vec {t}}={\begin{pmatrix}x_{c}\\y_{c}\end{pmatrix}}.$ = ( ${\vec {t}}={\begin{pmatrix}x_{c}\\y_{c}\end{pmatrix}}.$ x ${\vec {t}}={\begin{pmatrix}x_{c}\\y_{c}\end{pmatrix}}.$ ${\vec {t}}={\begin{pmatrix}x_{c}\\y_{c}\end{pmatrix}}.$ ${\vec {t}}={\begin{pmatrix}x_{c}\\y_{c}\end{pmatrix}}.$ ) ${\vec {t}}={\begin{pmatrix}x_{c}\\y_{c}\end{pmatrix}}.$ . ${\displaystyle {\vec{t}={\begin{pmatrix}x_{c}\y_{c}\end$ {pmatrix $}}}.$ $}$

각도 $α$ 에 의한 회전은 매트릭스 $A$ 를₃₃ 대각선으로 하여 실시할 수 있다. 따라서 $\lambda _{1}$ $\lambda _{1}$ ${\$ 및 $\lambda _{2}$ 2 ${\$ A의₃₃ 고유값이라면 중심 $\lambda _{2}$ 방정식은 새로운 변수 $x'$ 와 $y'$ 로^[9] 다시 쓸 수 있다.

\lambda_{1}x'^{2}+\lambda_{2}=-{\frac {\det A_{Q}}{\det A_{33}}}}.

$K=-{\frac {\det A_{Q}}{\det A_{33}}}$ = $K=-{\frac {\det A_{Q}}{\det A_{33}}}$ - $K=-{\frac {\det A_{Q}}{\det A_{33}}}$ $K=-{\frac {\det A_{Q}}{\det A_{33}}}$ Q $K=-{\frac {\det A_{Q}}{\det A_{33}}}$ A $K=-{\frac {\det A_{Q}}{\det A_{33}}}$ ${\$ 로 나누면 $K=-{\frac {\det A_{Q}}{\det A_{33}}}$ 표준 규격 형식을 얻는다.

예를 들어, 타원의 경우 이 양식은

{\frac {{x'}^{2}}:{a^{2}}+{\frac {{y'}^{2}}:{b^{2}}=1.

여기서부터 우리는 전통적인 표기법으로 반장축과 반소축의 $길이$ 인 $a$ 와 b를 얻는다.

중심 원뿔소의 경우 두 고유값은 모두 0이 아니며 원뿔 부분의 분류는 이를 조사하여 얻을 수 있다.^[10]

$만약 1$ and과 $algebra이 2$ 같은 대수 기호를 가지고 있다면, $K$ 가 같은 기호를 가지고 있거나, 반대 기호를 가지고 있거나, 0이면 $Q$ 는 실제 타원, 가상 타원 또는 실제 지점이다.
$만약 1$ and과 $λ$ 이₂ 반대 대수 부호를 가지고 있다면, $Q$ 는 각각 $K$ 가 0이 아닌지에 따라 하이퍼볼라 또는 두 개의 교차선이다.

축

주축 정리에 의해 중심 원뿔단면(엘립스 또는 하이퍼볼라)의 2차 형태 행렬의 2개의 고유 벡터는 직각(직교)이며, 각각 원뿔의 주축이나 부축과 (동일한 방향으로) 평행이다. 고유값이 가장 작은 고유값(절대값)을 갖는 고유 벡터는 주축에 해당한다.^[11]

특히 중심 원뿔 부분이 중심 $(x c c,$ y $)$ 을 가지며 $A$ 의₃₃ 고유 벡터가 v $\to(v 1,$ $v 2)$ 에 의해 주어진다면, 해당 고유벡터에 해당하는 주축(주축 또는 부축)은 방정식을 가진다.

{\frac {x-x_{c}{v_{1}}={\frac {y-y_{c}{v_{2}}.

정점

중심 원뿔의 정점은 원뿔과 그 축의 교차점 즉, 2차 원뿔 방정식과 축의 하나 또는 다른 축을 교대로 하는 선형 방정식으로 구성된 시스템을 풀어서 결정할 수 있다. 하이퍼볼라의 경우 부축이 실제 좌표가 있는 지점에서 하이퍼볼라와 교차하지 않기 때문에 각 축에 대해 두 개 또는 정점이 없다. 그러나, 복잡한 평면의 넓은 시야에서 보면, 하이퍼볼라의 작은 축은 하이퍼볼라와 교차하지만, 복잡한 좌표를 가진 지점에서 교차한다.^[12]

폴리스와 폴라

동일^[14] 좌표 사용,^[13] 점

\mathbf {p} ={\begin{pmatrix}p_{0}\\p_{1}\\p_{2}\end{pmatrix}}

and

\mathbf {r} ={\begin{pmatrix}r_{0}\\r_{1}\\r_{2}\end{pmatrix}}

제공된 원뿔 $Q$ 에 대해 결합한다.

\mathbf {p} ^{T}A_{Q}\mathbf {r} =0.

고정점 $p$ 의 결합체는 선을 형성하거나 원뿔의 평면에 있는 모든 점으로 구성된다. $p$ 의 결합체가 선을 형성하면 그 선을 $p$ 의 극이라고 하고, 점 $p$ 는 원뿔에 관해서 선의 극이라고 한다. 점과 선의 이러한 관계를 극성이라고 한다.

원뿔이 비감속인 경우, 어떤 점의 결합체는 항상 선을 형성하며 원뿔에 의해 정의되는 극성은 원뿔을 포함하는 확장면의 점 및 선(즉, 무한대의 점 및 선과 함께 평면) 사이의 편향이다.

$점$ p가 $원뿔$ Q에 놓여 있는 경우, $p$ 의 $극선$ 은 $p$ 에서 Q에 대한 접선 선이다.

비생성 원뿔 $Q$ 에 대한 $p$ 점의 극선(polar line)의 등식은 다음과 같다.

\mathbf {p} ^{T}A_{Q}{\begin{pmatrix}x\y\z\end{pmatrix}=0.

$p$ 가 (주어진 원뿔에 대하여) 극선을 고유하게 결정하듯이, 그래서 각 선은 고유한 극 $p$ 를 결정한다. 더욱이 p점 $p$ 는 $p점$ r의 극성을 통과한다면, 만약 $p$ 의 극성이 점 r(La Hire의 정리)을 통과하는 경우에만 점 $r$ 의 극인 $L선$ 에 있다.^[15] 따라서 이 관계는 평면에 있는 점과 선 사이의 기하학적 이중성의 표현이다.

원뿔 절에 관한 몇 가지 친숙한 개념은 이 극성과 직접 관련이 있다. 비탈진 원뿔의 중심은 무한에서 선의 극으로 식별할 수 있다. 포물선은 무한대의 선에 접하면 그 중심이 무한대의 선에 있는 지점이 될 것이다. 하이퍼볼라는 두 개의 뚜렷한 점에서 무한대의 선을 교차하며, 이 점들의 극선은 하이퍼볼라의 점증하지 않는 점이며, 무한대의 이 지점들에서 하이퍼볼라의 접선이다. 또한 원뿔의 포커스의 극선은 그에 상응하는 다이렉트릭스(directrix)이다.^[16]

접선

$L$ 선은 비감소 원뿔 $Q$ 에 대한 $p$ 점의 극선이 되도록 한다. 라 리터의 정리로는 $p$ 를 통과하는 모든 선은 $L$ 에 그 극을 두고 있다. 만약 $L$ 이 2점(가능한 최대치)에서 Q를 교차한다면, 그 점의 $폴라$ 는 p를 통과하는 접선이며, 그러한 $점$ 을 Q의 외부 또는 바깥쪽 점이라고 한다. $L$ 이 $1점$ 에서만 Q를 교차한다면 접선이며 $p$ 는 접선점이다. 마지막으로 $L$ 이 $Q$ 를 교차하지 않으면 $p$ 는 이를 통과하는 접선이 없으며 내점 또는 내점이라고 한다.^[17]

비생성 원뿔 $Q$ 의 $p$ 지점에서 접선 선(동일한 좌표)의 방정식은 다음과 같다.

\mathbf {p} ^{T}A_{Q}{\begin{pmatrix}x\y\z\end{pmatrix}=0.

$p$ 가 외부 점인 경우, 먼저 극성의 방정식(위 방정식)을 찾은 다음 원뿔과 그 선의 교차점을 찾는다( $s$ 와 $t$ ). $s$ 와 $t$ 의 폴라는 $p$ 를 통과하는 접선이 될 것이다.

극과 폴라의 이론을 이용하여 두 원뿔의 네 가지 상호 접선을 찾는 문제는 두 원뿔의 교차점을 찾는 것으로 줄어든다.

참고 항목

메모들

^ 브래넌, 에스플렌 & 그레이 1999, 페이지 30
^ Jump up to: ^a ^b 페토프레초 1978, 페이지 110
^ Jump up to: ^a ^b 2007년 스페인 페이지 59~62
^ 또한 2차 형태의 행렬이지만 이 형태는 세 $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ 의 변수를 가지며 A $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ + B $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ + C $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ 2 $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ + $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ z $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ + $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ + $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ F $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ ${\$ $Cy^{2}+Dxz+Eyz+Fz^{2$
^ 로렌스 1972 페이지 63
^ 2007년 스페인 페이지 70
^ 페토프레초 1978 페이지 105
^ 아유브 1993 페이지 322
^ 아유브 1993 페이지 324
^ 페토프레초 1978, 페이지 108
^ 오스터만 & 워너 2012, 페이지 311
^ Kendig, Keith (2005), Conics, The Mathematical Association of America, pp. 89–102, ISBN 978-0-88385-335-1
^ 이는 다음 결과 중 일부에 대해 필요한 무한점 및 무한점의 대수적 포함을 허용한다.
^ 이 절은 다음과 같다.
^ 브래넌, 에스플렌 & 그레이 1999, 페이지 189
^ Akopyan, A.V.; Zaslavsky, A.A. (2007), Geometry of Conics, American Mathematical Society, p. 72, ISBN 978-0-8218-4323-9
^ 복잡한 평면에서 그러한 점은 복잡한 $점$ 에서 Q를 충족하는 두 개의 복잡한 접선 선에 해석된다.

참조

Ayoub, A. B. (1993), "The central conic sections revisited", Mathematics Magazine, 66 (5): 322–325, doi:10.1080/0025570x.1993.11996157
Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1999), Geometry, Cambridge University Press, ISBN 978-0-521-59787-6
Lawrence, J. Dennis (1972), A Catalog of Special Plane Curves, Dover
Ostermann, Alexander; Wanner, Gerhard (2012), Geometry by its History, Springer, doi:10.1007/978-3-642-29163-0, ISBN 978-3-642-29163-0
Pettofrezzo, Anthony (1978) [1966], Matrices and Transformations, Dover, ISBN 978-0-486-63634-4
Spain, Barry (2007) [1957], Analytical Conics, Dover, ISBN 978-0-486-45773-4

[1] 브래넌, 에스플렌 & 그레이 1999, 페이지 30

[petto110-2] Jump up to: ^a ^b 페토프레초 1978, 페이지 110

[Spainsec-3] Jump up to: ^a ^b 2007년 스페인 페이지 59~62

[4] 또한 2차 형태의 행렬이지만 이 형태는 세 $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ 의 변수를 가지며 A $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ + B $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ + C $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ 2 $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ + $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ z $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ + $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ + $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ F $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ $Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}$ ${\$ $Cy^{2}+Dxz+Eyz+Fz^{2$

[Lawrence-5] 로렌스 1972 페이지 63

[6] 2007년 스페인 페이지 70

[7] 페토프레초 1978 페이지 105

[8] 아유브 1993 페이지 322

[9] 아유브 1993 페이지 324

[10] 페토프레초 1978, 페이지 108

[11] 오스터만 & 워너 2012, 페이지 311

[12] Kendig, Keith (2005), Conics, The Mathematical Association of America, pp. 89–102, ISBN 978-0-88385-335-1

[13] 이는 다음 결과 중 일부에 대해 필요한 무한점 및 무한점의 대수적 포함을 허용한다.

[14] 이 절은 다음과 같다.

[15] 브래넌, 에스플렌 & 그레이 1999, 페이지 189

[16] Akopyan, A.V.; Zaslavsky, A.A. (2007), Geometry of Conics, American Mathematical Society, p. 72, ISBN 978-0-8218-4323-9

[17] 복잡한 평면에서 그러한 점은 복잡한 $점$ 에서 Q를 충족하는 두 개의 복잡한 접선 선에 해석된다.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[14]

[13]

[15]

[16]

[17]

hide v t 매트릭스 클래스
명시적으로 제한된 항목	(0,1) 교번트 반대각형 반헤르미티아누스 반대칭 화살촉 밴드 비다이각형 이진수 이대칭 블록 대각선 블록 블록삼각형 부울 카우치 중심대칭 회의 콤플렉스 하다마드 코포시티브 대각선 우세 대각선 이산 푸리에 변환 초급 등가 프로베니우스 일반화 순열 하다마드 행클 에르미트어 헤센베르크 할로우 정수 논리적인 메츨러 무어 비음성 펜타디각형 순열 당칭 다항식 쿼터니온어 서명 싱글 엔트 스큐헤르미티안 스큐 대칭 스카이라인 스파스 실베스터 대칭 토플리츠 삼각형 삼두각형 유니타리 반데르몽드 월시 Z
상수	교환 힐베르트 아이덴티티 레머 1개 중 파스칼 파울리 레데퍼 시프트 영
고유값 또는 고유벡터 조건	동반자 수렴성 결함이 있는 대각선 가능 후르비츠 포지티브-확정성 슈틸트제스
제품 또는 역에 대한 만족도 조건	컨그루엔트 Idempotent 또는 Projection 되돌릴 수 없는 비자발적 닐포텐트 정상 직교 단모듈라 전지전능 완전히 단변성 체중 측정
특정 애플리케이션 사용	애드주게이트 교대 부호 증강됨 베주트 칼레만 카르탄 서큘런트 공동 인자 정류 혼란 콕시터 거리 중복 및 제거 유클리드 거리 기본(선형 미분 방정식) 제너레이터 그램 헤시안 세대주 야코비안 모멘트 모두 다 갚다, 청산하다 뽑다 무작위 회전 세이퍼트 전단 유사성 심플렉틱 완전히 긍정적이다. 변환
통계에 사용됨	센터링 상관 관계 공분산 디자인 이중 확률적 피셔 정보 모자 정밀도 스토카스틱 전이
그래프 이론에 사용됨	인접 바이애드제이컨시 정도 에드먼즈 발생 라플라시안 사이델 인접 투테
이공계에 사용됨	카비보-코바야시-마사와 밀도 기본(컴퓨터 비전) 퍼지 연관성 감마 겔만 해밀턴어 불규칙한 겹치다 S 국가전환 대체 Z(화학)
관련 용어	요르단 정상 형태 선형독립 행렬 지수 원뿔 단면의 행렬 표현 퍼펙트 매트릭스 사이비인버스 쿼터니온 행렬 행 에슐론 양식 룬스키안
행렬 목록 범주:행렬

Search