삼각함수를 포함하는 등호
삼각법 에서 삼각 항등식(三角 trig式, )은 삼각함수 를 포함하는 항등식 이며, 항등식의 양변이 정의되는 발생 변수 의 모든 값에 대해 참입니다.기하학적으로 이들은 하나 이상의 각도 의 특정 함수를 포함하는 항등식 입니다. 삼각형의 변의 길이 또는 삼각형 의 다른 길이를 포함하지만 각도를 포함할 가능성이 있는 삼각형 의 정체성과는 구별됩니다.
이러한 ID는 삼각 함수와 관련된 식을 단순화해야 할 때 유용합니다. 중요한 응용은 삼각함수가 아닌 함수의 통합 입니다. 일반적인 기술은 먼저 삼각함수를 가진 치환 규칙을 사용하고, 그 다음에 삼각함수 항등식을 사용하여 결과적인 적분을 단순화하는 것을 포함합니다.
피타고라스 정체성 단위 원에서의 삼각 함수 및 그 역수. 모든 직각 삼각형은 유사합니다. 즉, 대응하는 변 사이의 비율이 동일합니다. sin, cos 및 tan 단위 길이 반지름은 이들을 정의하는 삼각형의 빗변을 형성합니다. 역수 항등식은 삼각형에서 변의 비율로 발생하며, 이 단위선은 더 이상 빗변이 아닙니다. 파란색으로 표시된 삼각형은 아이덴티티 1 간이 2 csc 2 {\displaystyle 1+\cot ^{2}\theta csc ^{2}\theta } , tan 1 sec displaystyle \tan 2}\theta +1 sec 2}\theta } . 사인과 코사인 사이의 기본적인 관계는 피타고라스의 동일성에 의해 주어집니다.
죄악의 2 θ + cos 2 θ = 1 , {\displaystyle \sin ^{2}\theta +\cos ^{2}\theta = 1,}
여기서 sin 2 displaystyle \sin 2}\theta } sin ) {\displaystyle (\sin \theta )^{2}} cos 2 {\displaystyle \cos ^{2}\theta } cos ) 2 . {\displaystyle (\cos \theta )^{2}}
이것은 피타고라스 정리 의 버전으로 볼 수 있으며, 단위 원 에 대한 방정식 x 2 y 2 1 {\displaystyle x^{2} ^{2 1} 이 식을 사인 또는 코사인에 대해 풀 수 있습니다.
죄악의 θ = ± 1 − cos 2 θ , cos θ = ± 1 − 죄악의 2 θ . {\디스플레이 스타일 {\begin{aligned}\sin \theta &=\pm {\sqrt {1-\cos ^{2}\theta}},\cos \theta &=\pm {\sqrt {1-\sin ^{2}\theta}}. \end{aligned}}
부호 사분면 에 따라 달라집니다. {\displaystyle \theta .}
이 ID를 sin 2 {\displaystyle \sin ^{2}\theta }, cos 2 \cos ^{2}\theta }
1 + 간이 침대 2 θ = csc 2 θ 1 + 태닝한 2 θ = 초 2 θ 초 2 θ + csc 2 θ = 초 2 θ csc 2 θ {\디스플레이 스타일 {\begin{aligned}&1+\cot ^{2}\theta =\csc ^{2}\theta \&1+\tan ^{2}\theta =\sec ^{2}\theta \&\sec ^{2}\theta +\csc ^{2}\theta =\sec ^{2}\theta \csc ^{2}\theta \end{aligned}}
이러한 ID를 사용하면 삼각함수를 다른 용어(플러스 기호 또는 마이너스 기호 까지)로 표현할 수 있습니다.
각 삼각함수는 다른 다섯 개의 용어로 표시됩니다.[1] 측면에서. 죄악의 θ {\displaystyle \sin \theta} csc θ {\displaystyle \csc \theta} cos θ {\displaystyle \cos \theta} 초 θ {\displaystyle \sec \theta} 태닝한 θ {\displaystyle \tan \theta} 간이 침대 θ {\displaystyle \cot \theta} 죄악의 θ = {\displaystyle \sin \theta =} 죄악의 θ {\displaystyle \sin \theta} 1 csc θ {\displaystyle {\frac {1}{\csc \theta}}} ± 1 − cos 2 θ {\displaystyle \pm {\sqrt {1-\cos ^{2}\theta}}} ± 초 2 θ − 1 초 θ {\displaystyle \pm {\frac {\sqrt {\sec^{2}\theta -1}}{\sec \theta}}} ± 태닝한 θ 1 + 태닝한 2 θ {\displaystyle \pm {\frac {\tan \theta}{\sqrt {1+\tan^{2}\theta}}}}} ± 1 1 + 간이 침대 2 θ {\display style \pm {\frac {1}{\sqrt {1+\cot^{2}\theta}}}} csc θ = {\displaystyle \csc \theta =} 1 죄악의 θ {\displaystyle {\frac {1}{\sin \theta}}} csc θ {\displaystyle \csc \theta} ± 1 1 − cos 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1-\cos ^{2}\theta}}}}개 ± 초 θ 초 2 θ − 1 {\displaystyle \pm {\frac {\sec \theta}{\sqrt {\sec^{2}\theta -1}}}} ± 1 + 태닝한 2 θ 태닝한 θ {\displaystyle \pm {\frac {\sqrt {1+\tan^{2}\theta}}}{\tan \theta}}} ± 1 + 간이 침대 2 θ {\displaystyle \pm {\sqrt {1+\cot^{2}\theta}}} cos θ = {\displaystyle \cos \theta =} ± 1 − 죄악의 2 θ {\displaystyle \pm {\sqrt {1-\sin^{2}\theta}}} ± csc 2 θ − 1 csc θ {\displaystyle \pm {\frac {\sqrt {\csc ^{2}\theta -1}}{\csc \theta}}} cos θ {\displaystyle \cos \theta} 1 초 θ {\displaystyle {\frac {1}{\sec \theta}}} ± 1 1 + 태닝한 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1+\tan^{2}\theta}}}}개 ± 간이 침대 θ 1 + 간이 침대 2 θ {\display style \pm {\frac {\cot \theta}{\sqrt {1+\cot ^{2}\theta}}}}} 초 θ = {\displaystyle \sec \theta =} ± 1 1 − 죄악의 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1-\sin^{2}\theta}}}}개 ± csc θ csc 2 θ − 1 {\displaystyle \pm {\frac {\csc \theta}{\sqrt {\csc ^{2}\theta -1}}}} 1 cos θ {\displaystyle {\frac {1}{\cos \theta}}} 초 θ {\displaystyle \sec \theta} ± 1 + 태닝한 2 θ {\displaystyle \pm {\sqrt {1+\tan^{2}\theta}}} ± 1 + 간이 침대 2 θ 간이 침대 θ {\display style \pm {\frac {\sqrt {1+\cot^{2}\theta}}}{\cot \theta}}} 태닝한 θ = {\displaystyle \tan \theta =} ± 죄악의 θ 1 − 죄악의 2 θ {\displaystyle \pm {\frac {\sin \theta}{\sqrt {1-\sin ^{2}\theta}}}}} ± 1 csc 2 θ − 1 {\displaystyle \pm {\frac {1}{\sqrt {\csc ^{2}\theta -1}}}} ± 1 − cos 2 θ cos θ {\displaystyle \pm {\frac {\sqrt {1-\cos^{2}\theta}}}{\cos \theta}}}} ± 초 2 θ − 1 {\displaystyle \pm {\sqrt {\sec ^{2}\theta -1}} 태닝한 θ {\displaystyle \tan \theta} 1 간이 침대 θ {\displaystyle {\frac {1}{\cot \theta}}} 간이 침대 θ = {\displaystyle \cot \theta =} ± 1 − 죄악의 2 θ 죄악의 θ {\displaystyle \pm {\frac {\sqrt {1-\sin^{2}\theta}}}{\sin \theta}}} ± csc 2 θ − 1 {\displaystyle \pm {\sqrt {\csc ^{2}\theta -1}} ± cos θ 1 − cos 2 θ {\display style \pm {\frac {\cos \theta}{\sqrt {1-\cos ^{2}\theta}}}}} ± 1 초 2 θ − 1 {\displaystyle \pm {\frac {1}{\sqrt {\sec^{2}\theta -1}}}} 1 태닝한 θ {\displaystyle {\frac {1}{\tan \theta}}} 간이 침대 θ {\displaystyle \cot \theta}
반사, 이동, 주기성 단위 원을 조사함으로써 삼각 함수의 다음과 같은 성질을 확립할 수 있습니다.
리플렉션 반사각 α {\ displaystyle \alpha {\frac {\pi}{4}} a ,b ) 유클리드 벡터의 방향을 각도 θ, {\displaystyle \theta,} x {\displaystyle x} 원점과 양의 x {\displaystyle x} 축 방향 {\displaystyle \theta} α, {\displaystyle \alpha,} '{\ displaystyle \theta^{\prime}}
θ ′ = 2 α − θ . {\displaystyle \theta^{\prime }=2\alpha -\theta .}
특정 각도 α {\displaystyle \alpha} displaystyle \theta,\;\theta^{\prime}} 이것들은 환원 공식 으로도 알려져 있습니다.[2]
θ α = {\displaystyle \theta 반영 \al p ha 0} 홀수/짝수 신분 θ α π displaystyle theta displaystyle \al p ha frac {\pi}{4}} θ α π displaystyle theta} displaystyle \al p ha frac {\pi}{2}} θ α = 3 π {\displaystyle \theta} \al p ha frac {3\pi}{4}} θ α π displaystyle \theta} \al p ha pi} α 0 {\displaystyle \alpha 0} 죄악의 ( − θ ) = − 죄악의 θ {\displaystyle \sin (-\theta )=-\sin \theta } 죄악의 ( π 2 − θ ) = cos θ {\displaystyle \sin \left ({\tfrac {\pi}{2}}-\theta \right)=\cos \theta } 죄악의 ( π − θ ) = + 죄악의 θ {\displaystyle \sin(\pi -\theta )= +\sin \theta } 죄악의 ( 3 π 2 − θ ) = − cos θ {\displaystyle \sin \left ({\tfrac {3\pi}{2}}-\theta \right)=-\cos \theta } 죄악의 ( 2 π − θ ) = − 죄악의 ( θ ) = 죄악의 ( − θ ) {\displaystyle \sin(2\pi -\theta )=-\sin(\theta )=\sin (-\theta )} cos ( − θ ) = + cos θ {\displaystyle \cos (-\theta )= +\cos \theta } cos ( π 2 − θ ) = 죄악의 θ {\displaystyle \cos \left ({\tfrac {\pi}{2}}-\theta \right)=\sin \theta } cos ( π − θ ) = − cos θ {\displaystyle \cos(\pi -\theta )=-\cos \theta } cos ( 3 π 2 − θ ) = − 죄악의 θ {\displaystyle \cos \left ({\tfrac {3\pi}{2}}-\theta \right)=-\sin \theta } cos ( 2 π − θ ) = + cos ( θ ) = cos ( − θ ) {\displaystyle \cos(2\pi -\theta )= +\cos(\theta )=\cos (-\theta )} 태닝한 ( − θ ) = − 태닝한 θ {\displaystyle \tan (-\theta )=-\tan \theta } 태닝한 ( π 2 − θ ) = 간이 침대 θ {\display style \tan \left ({\tfrac {\pi}{2}}-\theta \right)=\cot \theta } 태닝한 ( π − θ ) = − 태닝한 θ {\displaystyle \tan(\pi -\theta )=-\tan \theta } 태닝한 ( 3 π 2 − θ ) = + 간이 침대 θ {\display style \tan \left ({\tfrac {3\pi}{2}}-\theta \right)=+\cot \theta } 태닝한 ( 2 π − θ ) = − 태닝한 ( θ ) = 태닝한 ( − θ ) {\displaystyle \tan(2\pi -\theta )=-\tan(\theta )=\tan (-\theta )} csc ( − θ ) = − csc θ {\displaystyle \csc (-\theta )=-\csc \theta } csc ( π 2 − θ ) = 초 θ {\displaystyle \csc \left ({\tfrac {\pi}{2}}-\theta \right)=\sec \theta } csc ( π − θ ) = + csc θ {\displaystyle \csc(\pi -\theta )= +\csc \theta } csc ( 3 π 2 − θ ) = − 초 θ {\displaystyle \csc \left ({\tfrac {3\pi}{2}}-\theta \right)=-\sec \theta } csc ( 2 π − θ ) = − csc ( θ ) = csc ( − θ ) {\displaystyle \csc(2\pi -\theta )=-\csc(\theta )=\csc (-\theta )} 초 ( − θ ) = + 초 θ {\displaystyle \sec (-\theta )= +\sec \theta } 초 ( π 2 − θ ) = csc θ {\displaystyle \sec \left ({\tfrac {\pi}{2}}-\theta \right) =\csc \theta } 초 ( π − θ ) = − 초 θ {\displaystyle \sec(\pi -\theta )=-\sec \theta } 초 ( 3 π 2 − θ ) = − csc θ {\displaystyle \sec \left ({\tfrac {3\pi}{2}}-\theta \right)=-\csc \theta } 초 ( 2 π − θ ) = + 초 ( θ ) = 초 ( − θ ) {\displaystyle \sec(2\pi -\theta )= +\sec(\theta )=\sec (-\theta )} 간이 침대 ( − θ ) = − 간이 침대 θ {\display style \cot (-\theta )=-\cot \theta } 간이 침대 ( π 2 − θ ) = 태닝한 θ {\displaystyle \cot \left ({\tfrac {\pi}{2}}-\theta \right)=\tan \theta } 간이 침대 ( π − θ ) = − 간이 침대 θ {\displaystyle \cot(\pi -\theta )=-\cot \theta } 간이 침대 ( 3 π 2 − θ ) = + 태닝한 θ {\display style \cot \left ({\tfrac {3\pi}{2}}-\theta \right)=+\tan \theta } 간이 침대 ( 2 π − θ ) = − 간이 침대 ( θ ) = 간이 침대 ( − θ ) {\display style \cot(2\pi -\theta )=-\cot(\theta )=\cot (-\theta )}
이동 및 주기성 각도 θ {\displaystyle \theta} frac {\pi}{2}} b ) 1/4주기 이동 1/2주기 시프트 기간별[4] 기간 죄악의 ( θ ± π 2 ) = ± cos θ {\displaystyle \sin(\theta \pm {\tfrac {\pi}{2}})=\pm \cos \theta } 죄악의 ( θ + π ) = − 죄악의 θ {\displaystyle \sin(\theta +\pi )=-\sin \theta } 죄악의 ( θ + k ⋅ 2 π ) = + 죄악의 θ {\displaystyle \sin(\theta +k\cdot 2\pi )= +\sin \theta } 2 π {\displaystyle 2\pi} cos ( θ ± π 2 ) = ∓ 죄악의 θ {\displaystyle \cos(\theta \pm {\tfrac {\pi}{2}})=\mp \sin \theta } cos ( θ + π ) = − cos θ {\displaystyle \cos(\theta +\pi )=-\cos \theta } cos ( θ + k ⋅ 2 π ) = + cos θ {\displaystyle \cos(\theta +k\cdot 2\pi )=+\cos \theta } 2 π {\displaystyle 2\pi} csc ( θ ± π 2 ) = ± 초 θ {\displaystyle \csc(\theta \pm {\tfrac {\pi}{2}})=\pm \sec \theta } csc ( θ + π ) = − csc θ {\displaystyle \csc(\theta +\pi )=-\csc \theta } csc ( θ + k ⋅ 2 π ) = + csc θ {\displaystyle \csc(\theta +k\cdot 2\pi )= +\csc \theta } 2 π {\displaystyle 2\pi} 초 ( θ ± π 2 ) = ∓ csc θ {\displaystyle \sec(\theta \pm {\tfrac {\pi}{2}})=\mp \csc \theta } 초 ( θ + π ) = − 초 θ {\displaystyle \sec(\theta +\pi )=-\sec \theta } 초 ( θ + k ⋅ 2 π ) = + 초 θ {\displaystyle \sec(\theta +k\cdot 2\pi )= +\sec \theta } 2 π {\displaystyle 2\pi} 태닝한 ( θ ± π 4 ) = 태닝한 θ ± 1 1 ∓ 태닝한 θ {\displaystyle \tan(\theta \pm {\tfrac {\pi}{4}})={\tfrac {\tan \teta \pm 1}{1\mp \tan \theta}} 태닝한 ( θ + π 2 ) = − 간이 침대 θ {\displaystyle \tan(\theta +{\tfrac {\pi}{2}})=-\cot \theta } 태닝한 ( θ + k ⋅ π ) = + 태닝한 θ {\displaystyle \tan(\theta +k\cdot \pi )=+\tan \theta } π {\displaystyle \pi} 간이 침대 ( θ ± π 4 ) = 간이 침대 θ ∓ 1 1 ± 간이 침대 θ {\displaystyle \cot(\theta \pm {\tfrac {\pi}{4}})={\tfrac {\cot \mp 1}{1\pm \cot \theta}}} 간이 침대 ( θ + π 2 ) = − 태닝한 θ {\displaystyle \cot(\theta +{\tfrac {\pi}{2}})=-\tan \theta } 간이 침대 ( θ + k ⋅ π ) = + 간이 침대 θ {\display style \cot(\theta +k\cdot \pi )=+\cot \theta } π {\displaystyle \pi}
징후 삼각함수의 부호는 각도의 사분면에 따라 달라집니다. - {\displaystyle {-\pi}<\theta \leq \pi} sgn 이 부호 함수 일 경우,
sgn ( 죄악의 θ ) = sgn ( csc θ ) = { + 1 한다면 0 < θ < π − 1 한다면 − π < θ < 0 0 한다면 θ ∈ { 0 , π } sgn ( cos θ ) = sgn ( 초 θ ) = { + 1 한다면 − 1 2 π < θ < 1 2 π − 1 한다면 − π < θ < − 1 2 π 아니면 1 2 π < θ < π 0 한다면 θ ∈ { − 1 2 π , 1 2 π } sgn ( 태닝한 θ ) = sgn ( 간이 침대 θ ) = { + 1 한다면 − π < θ < − 1 2 π 아니면 0 < θ < 1 2 π − 1 한다면 − 1 2 π < θ < 0 아니면 1 2 π < θ < π 0 한다면 θ ∈ { − 1 2 π , 0 , 1 2 π , π } {\displaystyle {\begin{aligned}\operatorname {sgn}(\sin \theta )=\operatorname {sgn}(\csc \theta )&={\begin{cases}+1&{\text{if}}\ \0<\theta <\pi \-1&{\text{if}}\{-\pi }\\\theta \in \{0,\pi \}\end{cases}}\[5mu]\operatorname {sgn}(\cos \theta )=\operatorname {sgn}(\sec \theta )&={\begin{cases}+1&{\text{if}}\{-{\tfr}\{\tfr} ac {1}{2}}\pi }<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\{-\pi }<\theta <-{\tfrac {1}{2}}\pi \{\text{or}}\pi \{\tfrac {1}{2}}\pi <\theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi }, {\tfrac {1}{2}}\pi {\bigr \}}\[5mu]\operatorname {sgn}(\tan \theta )=\operatorname {sgn}(\cot \teta )&={\tbegin{case}+1&{\t} ext{if}}\ \{-\pi}<\theta <-{\tfrac {1}{2}}\pi \{\text{or}}\0<\theta <{\tfrac {1}{2}}\pi \-1&{\text{if}}\pi \{-{\tfrac {1}{2}}\pi }<\theta <0\{\tfrac {1}{2}}\pi <\tfraq {\text{if}}\pi \theta \in {\bigl \{-{\tfrac {1}{2}}\pi },0,{\tfrac {1}{2}},\pi {\bigr \},\end{case}}\end{align}}}
삼각 함수는 공통 주기 2 , {\displaystyle 2\pi} ( , {\displaystyle ({-\pi },\pi }) 이동 및 주기성 참조).
각도합 및 차이 항등식 예각의 사인과 코사인에 대한 각도 추가 공식을 설명합니다. 강조된 세그먼트는 단위 길이입니다. sin α β ) {\displaystyle \sin(\alpha \beta )} cos α β ) {\displaystyle \cos(\alpha \beta )} . 이 는 각도 덧셈 및 뺄셈 정리 (또는 공식 )로도 알려져 있습니다.
죄악의 ( α + β ) = 죄악의 α cos β + cos α 죄악의 β 죄악의 ( α − β ) = 죄악의 α cos β − cos α 죄악의 β cos ( α + β ) = cos α cos β − 죄악의 α 죄악의 β cos ( α − β ) = cos α cos β + 죄악의 α 죄악의 β {\displaystyle {\begin{aligned}\sin(\alpha +\beta)&=\sin \alpha \cos \sin \sin \\alpha -\beta)&=\sin \alpha \cos \sin \sin \beta \\\cos \sin \sin \\alpha +\beta)&=\cos \alpha \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin
sin ( α β ) {\displaystyle \sin(\alpha \ )} 코스 ( α β ) {\displaystyle \cos(\alpha \ )} ( displaystyle sin ( β ) sin ( β ) {\displaystyle \sin si n(\beta )} cos β ) = cos β {\displaystyle \cos (- beta = cos(\ beta )}. 또한 각도 합 ID에 대해 그림을 약간 수정한 버전을 사용하여 이 값을 도출할 수 있습니다. 여기에는 두 개의 값이 모두 나와 있습니다.
이러한 항등식은 다음 표의 처음 두 행에 요약되어 있으며, 다른 삼각 함수에 대한 합 항등식과 차 항등식 항등식도 포함되어 있습니다.
사인 죄악의 ( α ± β ) {\displaystyle \sin(\alpha \pm \beta )} = {\displaystyle =} 죄악의 α cos β ± cos α 죄악의 β {\displaystyle \sin \alpha \cos \beta \pm \cos \alpha \sin \beta } [5] [6] 코사인 cos ( α ± β ) {\displaystyle \cos(\alpha \pm \beta )} = {\displaystyle =} cos α cos β ∓ 죄악의 α 죄악의 β {\displaystyle \cos \alpha \cos \beta \mp \sin \alpha \sin \beta } [6] [7] 접선 태닝한 ( α ± β ) {\displaystyle \tan(\alpha \pm \beta )} = {\displaystyle =} 태닝한 α ± 태닝한 β 1 ∓ 태닝한 α 태닝한 β {\displaystyle {\frac {\tan \alpha \pm \tan \tan \beta }{1\mp \tan \alpha \tan \tan \beta }} [6] [8] 보조금 csc ( α ± β ) {\displaystyle \csc(\alpha \pm \beta )} = {\displaystyle =} 초 α 초 β csc α csc β 초 α csc β ± csc α 초 β {\displaystyle {\frac {\sec \alpha \sec \beta \csc \csc \csc \beta }{\sec \alpha \csc \beta \pm \csc \alpha \sec \sec \beta }} [9] 세컨트 초 ( α ± β ) {\displaystyle \sec(\alpha \pm \beta )} = {\displaystyle =} 초 α 초 β csc α csc β csc α csc β ∓ 초 α 초 β {\displaystyle {\frac {\sec \alpha \sec \beta \csc \csc \csc \beta }{\csc \alpha \csc \csc \beta \mp \sec \alpha \sec \beta }} [9] 코탄젠트 간이 침대 ( α ± β ) {\displaystyle \cot(\alpha \pm \beta )} = {\displaystyle =} 간이 침대 α 간이 침대 β ∓ 1 간이 침대 β ± 간이 침대 α {\display style {\frac {\cot \alpha \cot \mp 1}{\cot \beta \pm \cot \alpha }} [6] [10] 아크신 호신 x ± 호신 y {\displaystyle \arcsin x\pm \arcsiny} = {\displaystyle =} 호신 ( x 1 − y 2 ± y 1 − x 2 ) {\displaystyle \arcsin \left(x{\sqrt {1-y^{2}}}\pm y{\sqrt {1-x^{2}}\right)} [11] 아르코신 아코코 x ± 아코코 y {\displaystyle \arccos x\pm \arccosy} = {\displaystyle =} 아코코 ( x y ∓ ( 1 − x 2 ) ( 1 − y 2 ) ) {\displaystyle \arccos \left(xy\mp {\sqrt {\left(1-x^{2}\right)\left(1-y^{2}\right)}}\right)} [12] 아크탄젠트 아크탄 x ± 아크탄 y {\displaystyle \arctan x\pm \arctan} = {\displaystyle =} 아크탄 ( x ± y 1 ∓ x y ) {\displaystyle \arctan \left ({\frac {x\pmy}{1\mp xy}}\right)} [13] 아코탄젠트 아궁이 x ± 아궁이 y {\displaystyle \operator name {arccot} x\pm \operator name {arccot} y} = {\displaystyle =} 아궁이 ( x y ∓ 1 y ± x ) {\displaystyle \operatorname {arccot} \left ({\frac {xy\mp 1}{y\pm x}}\right)}
무한히 많은 각도의 합의 사인과 코사인 급수 ∑ i 1 i {\textstyle \sum _{i 1}^{\infty}\theta _{i}} 수렴 할 때
죄악의 ( ∑ i = 1 ∞ θ i ) = ∑ 이상한 k ≥ 1 ( − 1 ) k − 1 2 ∑ A ⊆ { 1 , 2 , 3 , … } A = k ( ∏ i ∈ A 죄악의 θ i ∏ i ∉ A cos θ i ) cos ( ∑ i = 1 ∞ θ i ) = ∑ 심지어. k ≥ 0 ( − 1 ) k 2 ∑ A ⊆ { 1 , 2 , 3 , … } A = k ( ∏ i ∈ A 죄악의 θ i ∏ i ∉ A cos θ i ) . {\displaystyle {\begin{aligned}\sin \left(\sum _{i=1}^{\infty})\theta _{i}\right)&=\sum _{{\text{odd}}\k\geq 1}(-1)^{\frac {k-1}{2}}\sum _{\begin{smallmatrix} A\subseteq \{\,1,2,3,\dots \,\}\left A\right =k\end{smallmatrix}}\left(\prod _{i\in A}\sin \theta _{i}\cos \theta _{i}\right) \\cos \left(\sum _{i=1}^{\infty}}\theta _{i}\right)&=\sum _{{\text{even}}\k\geq 0}~(-1)^{\frac {k}{2}}~~\sum _{\begin{소행렬} A\subseteq \{\,1,2,3,\dots \,\}\left A\right =k\end{smallmatrix}}\left(\prod _{i\in A}\sin \theta _{i}\cos \theta _{i}\right). \end{aligned}}
급수 ∑ i 1 i {\textstyle \sum _{i 1}^{\infty }\theta {i}} lim i i 0 , {\textstyle \lim _{i\to \infty }\theta {i 0,} lim i sin i 0 , {\textstyle \lim _{i\to \infty }\sin \theta {i 0,}, lim i cos i 1 {i\to \infty }\cos the ta_{i}=1.} 유한개 의 코사인 인자가 있습니다.사인 인자가 무한히 많은 항은 반드시 0과 같습니다.
θ i {\displaystyle theta {i} 중 게다가, 각 항에서 코사인 인자들 중 유한한 것을 제외한 모든 코사인 인자들은 통일성입니다.
합접선과 공접선 k {\displaystyle e_{k}}( k 0 , 1 , 2 , 3 {\displaystyle 0, 1, 2, 3,\ldots } ) 대칭 다항식 이라고 합니다.
x i = 태닝한 θ i {\displaystyle x_{i}=\tan \theta _{i}} i 0 , 1 , 2 , 3 , …, {\displaystyle 0, 1, 2, ,\ldots ,} e 0 = 1 e 1 = ∑ i x i = ∑ i 태닝한 θ i e 2 = ∑ i < j x i x j = ∑ i < j 태닝한 θ i 태닝한 θ j e 3 = ∑ i < j < k x i x j x k = ∑ i < j < k 태닝한 θ i 태닝한 θ j 태닝한 θ k ⋮ ⋮ {\begin{aligned}e_{0}&=1\[6pt]e_{1}&=\sum _{i}x_{i}&=\sum _{i}\tan \theta _{i}&=\[6pt]e_{2}&=\sum _{i<j}x_{i}x_{j}&=\sum _{i<j}\tan \theta _{i}\tan \theta _{j}\[6pt]e_{3}&=\sum _{i<j<k}x_{i}x_{k}&=\sum _{i<j<k}\tan \theta _{j}\tan \theta _{j}\tan \theta _{k}\tan \theta _{k}\tan \dots &{}\dots \end{align}}}
그리고나서
태닝한 ( ∑ i θ i ) = 죄악의 ( ∑ i θ i ) / ∏ i cos θ i cos ( ∑ i θ i ) / ∏ i cos θ i = ∑ 이상한 k ≥ 1 ( − 1 ) k − 1 2 ∑ A ⊆ { 1 , 2 , 3 , … } A = k ∏ i ∈ A 태닝한 θ i ∑ 심지어. k ≥ 0 ( − 1 ) k 2 ∑ A ⊆ { 1 , 2 , 3 , … } A = k ∏ i ∈ A 태닝한 θ i = e 1 − e 3 + e 5 − ⋯ e 0 − e 2 + e 4 − ⋯ 간이 침대 ( ∑ i θ i ) = e 0 − e 2 + e 4 − ⋯ e 1 − e 3 + e 5 − ⋯ {\displaystyle {\begin{aligned}\tan \left(\sum _{i}\theta _{i}\right)&={\frac {\sin \left(\sum _{i}\theta _{i}\right)/\prod _{i}\cos \theta _{i}\right)\cos \left(\sum _{i}\cos \theta _{i}\cos \theta _{i}}\&={\frac {\displaystyle \sum _{\text{odd}}\k\geq 1(-1)^{\frac {k-1}{2}}\sum {\begin{smallmatrix}}\cos \left(\sum _{i})\cos \left(\sum _{i}\text_right}\cos \theta _{i}\cos \theta _right)\cos \theta _{i}\cos \theta _{i}\cos \theta _{i}\cos \theta _{i}\cos \theta _{i}}\ A\subseteq \{\,1,2,3,\dots \,\}\left A\right = k\end{smallmatrix}}\tan \theta _{i}}\tan \theta _{i}}\displaystyle \sum _{\text{even}\k\geq 0}~(-1)^{\frac {k}{2}~\sum _{\begin{smallmatrix} A\subseteq \{\,1,2,3,\dots \,\}\\left A\right =k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-{e_{2}+e_{4}-\cdots }\\\cdots \left(\sum _{i}\theta _{i}\right)&={\frac {e_0}-e_{2}+e_{4}-\cdots }{e_1}-e_{3}+e_{5}-\cdots }}\end{aligned}} 위의 사인과 코사인 합 공식을 사용합니다.
오른쪽의 항 수는 왼쪽의 항 수에 따라 달라집니다.
예를 들어,
태닝한 ( θ 1 + θ 2 ) = e 1 e 0 − e 2 = x 1 + x 2 1 − x 1 x 2 = 태닝한 θ 1 + 태닝한 θ 2 1 − 태닝한 θ 1 태닝한 θ 2 , 태닝한 ( θ 1 + θ 2 + θ 3 ) = e 1 − e 3 e 0 − e 2 = ( x 1 + x 2 + x 3 ) − ( x 1 x 2 x 3 ) 1 − ( x 1 x 2 + x 1 x 3 + x 2 x 3 ) , 태닝한 ( θ 1 + θ 2 + θ 3 + θ 4 ) = e 1 − e 3 e 0 − e 2 + e 4 = ( x 1 + x 2 + x 3 + x 4 ) − ( x 1 x 2 x 3 + x 1 x 2 x 4 + x 1 x 3 x 4 + x 2 x 3 x 4 ) 1 − ( x 1 x 2 + x 1 x 3 + x 1 x 4 + x 2 x 3 + x 2 x 4 + x 3 x 4 ) + ( x 1 x 2 x 3 x 4 ) , {\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2})&={\frac {e_{1}}{e_0}-e_{2}}={\frac {x_{1}+x_{2}} }}:{1\ -\x_{1}x_{2}}={\frac {\tan \theta _{1}+\tan \theta _{2}}{1\ -\tan \theta _{1}\tan \theta _{2}}},\[8pt]\tan(\theta _{1}+\tan_{2}+\tan(\theta _{3})&={\frac {e_{1}-e_{3}}{e_0}-e_{2}}={\frac {(x_1}+x_{2}+x_{3}}\ -\(x_1}x_{2}){1\ - (x_1}x_{2}+x_1}}{1\ - (x_1}x_{2}+x_{1}}}{1} }x_{3}+x_{2 }x_{3}},\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4} }}\[8pt]&={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\\\(x_{1}x_{2}x_{3}+x_{1) }x_{2}x_{4}+x_{1 }x_{3}x_{4}+x_{2 }x_{3}x_{4}}{1\ -\ (x_{1}x_{2}+x_{1) }x_{3}+x_{1 }x_{4}+x_{2 }x_{3}+x_{2 }x_{4}+x_{3 }x_{4})\ +\(x_{1}x_{2}x_{3}x_{4}},\end{aligned}}
등등. 한정적으로 많은 항들의 경우는 수학적 귀납법 으로 증명될 수 있습니다.[14]
여집합과 여집합
초 ( ∑ i θ i ) = ∏ i 초 θ i e 0 − e 2 + e 4 − ⋯ csc ( ∑ i θ i ) = ∏ i 초 θ i e 1 − e 3 + e 5 − ⋯ {\displaystyle {\begin{aligned}\sec \left(\sum _{i}\theta _{i}\right)&={\frac {\prod_{i}\sec \theta _{i}}{e_{2}+e_{4}-\cdots}}\\[8pt]\csc \left(\sum _{i}\theta _{i}\right)&={\frac {\prod_{i}\sec \theta _{i}{e_1}-e_{3}+e_{5}-\cdots}}\end{aligned}} 여기서 ek {\displaystyle e_{k}} n개 변수 xi tan , {\displaystyle x_{i tan \theta _{i} i 1 , …, n , {\displaystyle ,\ldots,n, } [15] 한정적으로 많은 항들의 경우는 그러한 항들의 수에 대한 수학적 귀납법으로 증명될 수 있습니다.
예를들면,
초 ( α + β + γ ) = 초 α 초 β 초 γ 1 − 태닝한 α 태닝한 β − 태닝한 α 태닝한 γ − 태닝한 β 태닝한 γ csc ( α + β + γ ) = 초 α 초 β 초 γ 태닝한 α + 태닝한 β + 태닝한 γ − 태닝한 α 태닝한 β 태닝한 γ . {\displaystyle {\begin{aligned}\sec(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \gamma }{1-\tan \alpha \tan \alpha \tan \tan \tan \gamma }}\[8pt]\csc(\alpha +\beta +\cgamma )&={\frac {\sec \alpha +\alpha \sec \sec \beta gamma }{\tan \alpha +\tan \alpha \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \tan \end{aligned}}
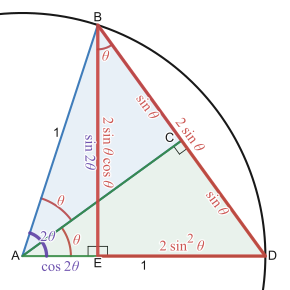
프톨레마이오스 정리 Ptolemy의 정리와 사인에 대한 각합 트리그 항등식 사이의 관계를 보여주는 다이어그램. 프톨레마이오스의 정리는 반대변의 길이의 곱의 합은 대각선의 길이의 곱과 같다는 것입니다. 위의 그림에 표시된 sin 및 cos 값으로 측면 lengths을 표현하면 사인에 대한 각도 합 삼각함수 동일성이 산출됩니다: sin(α + β ) = sin α cos β cos α sin β 프톨레마이오스의 정리는 사인과 코사인의 합 공식과 차 공식에 해당하는 결과가 처음으로 증명되었기 때문에 삼각 항등식의 역사에서 중요합니다. 그것은 첨부된 그림과 같이, 사변형 ABCD {\displaystyle ABCD} 대각선이나 변 중 하나가 원의 지름인 특수한 경우, 이 정리는 각도 합과 차이 삼각형 항등식을 직접적으로 발생시킵니다.[16] 이 관계는 원이 여기와 같이 길이 1의 직경을 갖도록 구성될 때 가장 쉽게 따라갑니다.
탈레스 정리 에 의해 ∠ DAB {\displaystyle \angle DAB} DCB {\displaystyle \angle DCB} 직각 삼각형 DAB {\displaystyle DAB} DCB {\displaystyle DCB} BD {\displaystyle {\overline }} 따라서 측면 A B sin {\overline {AB sin \alpha A cos α {\overline {AD cos \alpha C sin β {\overline {BC sin D cos β {\overline {CD cos
내접 각도 정리에 의해, 원의 중심에서 코드 AC {\displaystyle {\overline {AC}} A C {\displaystyle \angle ADC 2 α β {\displaystyle 2(\alpha +\beta )}. 따라서 대칭적인 빨간색 삼각형 쌍은 각각 중앙에각도 β {\displaystyle \alpha +\beta } 이 삼각형들 각각은 길이 1 2 {\textstyle {\frac {1}{2}} , AC {\displaystyle {\overline {AC}} 12 sin ( α β ) {\textstyle 2\times {\frac {1}{2}}\sin(\alpha +\beta )} , sin ( α β {\displaystyle \sin(\alpha +\beta )} . 사각형의 다른 대각선은 길이 1의 지름이므로 대각선 길이의 곱도 sin α β ) {\displaystyle \sin(\alpha +\beta )} .
이 C B D A B CD A B {\ displaystyle {\overline {AC}} \cdot {\overline {\overline {AB} \cdot {\overline {CD} {\overline {AD} \cdot {\overline {BC}} } sin α β ) sin . α cos β cos sin β {\displaystyle \sin(\alpha + \bet a ) sin \alpha \cos \alpha \sin \ sin beta ( α displaystyle \sin - \bet 마찬가지 B ¯ {\ CD} CD {\ displaystyle {\overline {} BD [17]
다각 공식 T 는n n번째 체비셰프 다항식 cos ( n θ ) = T n ( cos θ ) {\displaystyle \cos(n\theta )= T_{n}(\cos \theta )} [18] de Moivre의 공식 , i 는 허수 단위 입니다. cos ( n θ ) + i 죄악의 ( n θ ) = ( cos θ + i 죄악의 θ ) n {\displaystyle \cos(n\theta )+i\sin(n\theta )= (\cos \theta +i\sin \theta )^{n} [19]
다각 공식 쌍각 공식 사인에 대한 이중 각도 공식의 시각적 시연. 그 지역, 이등변 삼각형의 1 / 2 직립하면 영역 = sin cos {\displaystyle \sin \theta \cos \theta }, sin 2 {\textstyle {\frac {1}{2}}\sin 2\theta }. 따라서 sin 2 2 sin 코스 {\displaystyle \sin 2\theta 2\sin \theta \cos \theta .} 각 2배의 공식.[20]
죄악의 ( 2 θ ) = 2 죄악의 θ cos θ = ( 죄악의 θ + cos θ ) 2 − 1 = 2 태닝한 θ 1 + 태닝한 2 θ {\displaystyle \sin(2\theta )=2\sin \theta \cos \theta =(\sin \theta +\cos \theta )^{2}-1={\frac {2\tan \theta }{1+\tan ^{2}\theta }} cos ( 2 θ ) = cos 2 θ − 죄악의 2 θ = 2 cos 2 θ − 1 = 1 − 2 죄악의 2 θ = 1 − 태닝한 2 θ 1 + 태닝한 2 θ {\displaystyle \cos(2\theta )=\cos ^{2}\cos ^{2}\theta = 2\cos ^{2}\theta -1=1-2\sin ^{2}\theta = {\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta } 태닝한 ( 2 θ ) = 2 태닝한 θ 1 − 태닝한 2 θ {\displaystyle \tan(2\theta)={\frac {2\tan \theta}{1-\tan^{2}\theta}}} 간이 침대 ( 2 θ ) = 간이 침대 2 θ − 1 2 간이 침대 θ = 1 − 태닝한 2 θ 2 태닝한 θ {\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }={\frac {1-\tan ^{2}\theta }{2\tan \theta }} 초 ( 2 θ ) = 초 2 θ 2 − 초 2 θ = 1 + 태닝한 2 θ 1 − 태닝한 2 θ {\displaystyle \sec(2\theta )={\frac {\sec ^{2}\theta }{2-\sec ^{2}\theta }={\frac {1+\tan ^{2}\theta }{1-\tan ^{2}\theta }} csc ( 2 θ ) = 초 θ csc θ 2 = 1 + 태닝한 2 θ 2 태닝한 θ {\displaystyle \csc(2\theta )={\frac {\sec \csc \theta }{2}}={\frac {1+\tan^{2}\theta }{2\tan \theta }} 삼중각 공식 세 개의 각도에 대한 공식.[20]
죄악의 ( 3 θ ) = 3 죄악의 θ − 4 죄악의 3 θ = 4 죄악의 θ 죄악의 ( π 3 − θ ) 죄악의 ( π 3 + θ ) {\displaystyle \sin(3\theta )=3\sin \theta -4\sin ^{3}\theta =4\sin \theta \sin \left ({\frac {\pi}{3}-\theta \right)\sin \left ({\frac {\pi}{3}+\theta \right)} cos ( 3 θ ) = 4 cos 3 θ − 3 cos θ = 4 cos θ cos ( π 3 − θ ) cos ( π 3 + θ ) {\displaystyle \cos(3\theta )=4\cos ^{3}\theta -3\cos \theta =4\cos \theta \left ({\frac {\pi}{3}-\theta \right)\cos \left ({\frac {\pi}{3}+\theta \right)} 태닝한 ( 3 θ ) = 3 태닝한 θ − 태닝한 3 θ 1 − 3 태닝한 2 θ = 태닝한 θ 태닝한 ( π 3 − θ ) 태닝한 ( π 3 + θ ) {\displaystyle \tan(3\theta )={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}=\tan \theta \tan \tan \left ({\frac {\pi }{3}-\theta \right)\tan \left ({\frac {\pi }{3}+\theta \right)} 간이 침대 ( 3 θ ) = 3 간이 침대 θ − 간이 침대 3 θ 1 − 3 간이 침대 2 θ {\displaystyle \cot(3\theta)={\frac {3\cot \theta -\cot ^{3}\theta}{1-3\cot ^{2}\theta}} 초 ( 3 θ ) = 초 3 θ 4 − 3 초 2 θ {\displaystyle \sec(3\theta )={\frac {\sec ^{3}\theta}{4-3\sec ^{2}\theta}}} csc ( 3 θ ) = csc 3 θ 3 csc 2 θ − 4 {\displaystyle \csc(3\theta )={\frac {\csc ^{3}\theta}{3\csc ^{2}\theta -4}} 다각 및 반각 공식 여러 각도에 대한 공식.[21]
죄악의 ( n θ ) = ∑ k 이상한 ( − 1 ) k − 1 2 ( n k ) cos n − k θ 죄악의 k θ = 죄악의 θ ∑ i = 0 ( n + 1 ) / 2 ∑ j = 0 i ( − 1 ) i − j ( n 2 i + 1 ) ( i j ) cos n − 2 ( i − j ) − 1 θ = 2 ( n − 1 ) ∏ k = 0 n − 1 죄악의 ( k π / n + θ ) {\displaystyle {\begin{aligned}\sin(n\theta)&=\sum _{k{\text{odd}}(-1)^{\frac {k-1}{2}}{n \choose k}\cos ^{n-k}\theta \sin ^{k}\theta =\sin \theta \sum _{i=0}^{(n+1)/2}\sum _{j=0}^{i}(-1)^{i-j}{n \choose j}\cos ^{n-2(i-j)-1}\theta \{}&=2^{(n-1)}\prod _{k=0}^{n-1}\sin(k\pi /n+\theta )\end{aligned}} cos ( n θ ) = ∑ k 심지어. ( − 1 ) k 2 ( n k ) cos n − k θ 죄악의 k θ = ∑ i = 0 n / 2 ∑ j = 0 i ( − 1 ) i − j ( n 2 i ) ( i j ) cos n − 2 ( i − j ) θ {\displaystyle \cos(n\theta )=\sum _{k{\text{even}}(-1)^{\frac {k}{2}}{n \choose k}\cos ^{n-k}\theta \sin ^{k}\sin ^{n=0}^{n/2}\sum _{j=0}^{i}(-1)^{i-j}{n \choose 2i}{i \choose j}\cos ^{n-2(i-j)}\theta } cos ( ( 2 n + 1 ) θ ) = ( − 1 ) n 2 2 n ∏ k = 0 2 n cos ( k π / ( 2 n + 1 ) − θ ) {\displaystyle \cos((2n+1)\theta )= (-1)^{n}2^{2n}\prod_{k=0}^{2n}\cos(k\pi /(2n+1)-\theta )} cos ( 2 n θ ) = ( − 1 ) n 2 2 n − 1 ∏ k = 0 2 n − 1 cos ( ( 1 + 2 k ) π / ( 4 n ) − θ ) {\displaystyle \cos(2n\theta )= (-1)^{n}2^{2n-1}\prod_{k=0}^{2n-1}\cos((1+2k)\pi /(4n)-\theta )} 태닝한 ( n θ ) = ∑ k 이상한 ( − 1 ) k − 1 2 ( n k ) 태닝한 k θ ∑ k 심지어. ( − 1 ) k 2 ( n k ) 태닝한 k θ {\displaystyle \tan(n\theta )={\frac {\text{ odd}}(-1)^{\frac {k-1}{2}}{n \choose k}\tan ^{k}\theta }{\sum _{k{\text{even}}(-1)^{n \choose k}\tan ^{k}\theta }} 체비셰프법 체비셰프 방법은 n 1 ) {\displaystyle (n-1)} n 2 ) {\displaystyle (n-1) 재귀적 알고리즘 입니다.[22]
cos ( n x {\displaystyle \cos(nx)} ) c os ( n 1 x {\displaystyle \cos((n-1)x)}, c os (( n 2 ) x displaystyle \cos(( n x)} c os ( x ) .
cos ( n x ) = 2 cos x cos ( ( n − 1 ) x ) − cos ( ( n − 2 ) x ) . {\displaystyle \cos(nx)=2\cos x\cos((n-1)x)-\cos((n-1)x)}
이것은 공식들을 더하면 증명될 수 있습니다.
cos ( ( n − 1 ) x + x ) = cos ( ( n − 1 ) x ) cos x − 죄악의 ( ( n − 1 ) x ) 죄악의 x cos ( ( n − 1 ) x − x ) = cos ( ( n − 1 ) x ) cos x + 죄악의 ( ( n − 1 ) x ) 죄악의 x {\displaystyle {\begin{aligned}\cos((n-1)x+x)&=\cos(n-1)x\cos x-\sin(n-1)x)\sin x\\cos(n-1)x-x)&=\cos(n-1)x+\sin(n-1)x\sin x\end{aligned}}
유도에 의해 cos n x ) {\displaystyle \cos(nx)} cos x , {\displaystyle \cos x,} 체비셰프 다항식 을 참조하십시오. #삼각형 정의 .
마찬가지로 sin ( n x ) {\displaystyle \sin(nx)} sin ( n - 1 ) ), {\displaystyle \sin((n-1)x)}, {\displaystyle \sin((n 2 )x)} 및 cos x {\displaystyle \cos }
죄악의 ( n x ) = 2 cos x 죄악의 ( ( n − 1 ) x ) − 죄악의 ( ( n − 2 ) x ) {\displaystyle \sin(nx)=2\cos x\sin((n-1)x)-\sin((n-1)x)} 이는 sin (( n 1 x {\displaystyle \sin((n-1) )} sin (( n 1 x x ) . {\displaystyle \sin((n-1) )}
체비셰프 방법과 유사한 목적을 달성하기 위해 접선에 대해 다음과 같이 쓸 수 있습니다.
태닝한 ( n x ) = 태닝한 ( ( n − 1 ) x ) + 태닝한 x 1 − 태닝한 ( ( n − 1 ) x ) 태닝한 x . {\displaystyle \tan(nx)={\frac {\tan((n-1)x)+\tan x}{1-\tan((n-1)x)\tan x}},}
반각 공식
죄악의 θ 2 = sgn ( 죄악의 θ 2 ) 1 − cos θ 2 cos θ 2 = sgn ( cos θ 2 ) 1 + cos θ 2 태닝한 θ 2 = 1 − cos θ 죄악의 θ = 죄악의 θ 1 + cos θ = csc θ − 간이 침대 θ = 태닝한 θ 1 + 초 θ = sgn ( 죄악의 θ ) 1 − cos θ 1 + cos θ = − 1 + sgn ( cos θ ) 1 + 태닝한 2 θ 태닝한 θ 간이 침대 θ 2 = 1 + cos θ 죄악의 θ = 죄악의 θ 1 − cos θ = csc θ + 간이 침대 θ = sgn ( 죄악의 θ ) 1 + cos θ 1 − cos θ 초 θ 2 = sgn ( cos θ 2 ) 2 1 + cos θ csc θ 2 = sgn ( 죄악의 θ 2 ) 2 1 − cos θ {\displaystyle {\begin{aligned}\sin {\frac {\theta}{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta}{2}}\right){\sqrt {\frac {1-\cos \theta}{2}}\[3pt]\cos {\frac {\theta}{2}&=\operatorname {sgn} \left(\cos {\frac {\theta}{2}}\right){\sqrt {\frac {1+\cos \theta}{2}}\[3pt]\tan {\frac {\theta}{2}}&={\frac {1-\cos \theta}{\sin \theta}}}\tan {\frac {\frac {1-\cos \theta}}}{\sin \theta}}} ={\frac {\sin \theta }{1+\cos \theta }}=\csc \theta -\cot \theta ={\frac {\tan \theta }{1+\sec {\theta }}\[6mu]& =\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}={\frac {-1+\operatorname {sgn}(\cos \theta )}{\sqrt {1+\tan ^{2}\theta }}{\t}\cot {\frac {\theta }{2}}&={\frac {1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }=\csc \theta +\cot \theta =\operatorname {sgn}(\sin \theta ){\sqrt. {\frac {1+\cos \theta}{1-\cos \theta}}}\\sec {\frac {\theta}{2}}&=\operator name {sgn} \left(\cos {\frac {\theta}{2}\right){\sqrt {\frac {2}{1+\cos \theta}}\\csc {\frac {\theta}{2}&=\operator name {sgn} \left(\sin {\frac {\theta}{2}\right){\frac {2}}\\end {aligned}} [23] [24]
또한.
태닝한 η ± θ 2 = 죄악의 η ± 죄악의 θ cos η + cos θ 태닝한 ( θ 2 + π 4 ) = 초 θ + 태닝한 θ 1 − 죄악의 θ 1 + 죄악의 θ = 1 − 태닝한 θ 2 1 + 태닝한 θ 2 {\displaystyle {\begin{aligned}\tan {\frac {\eta \pm \theta}{2}}&={\frac {\sin \pm \theta}{\cos \eta +\cos \theta }}\[3pt]\tan \left ({\frac {\theta}{2}+{\frac {\pi}{4}\right)&=\sec \theta +\tan \theta \[3pt]{\sqrt {\frac {1-\sin \theta }}&={\frac {\left 1-\tan {\theta}{2}}\right }{\left 1+\tan {\frac {\frac {\the ta }{2}}\right }}\end{aligned}}
테이블 이들은 합과 차 항등식 또는 다각 공식을 사용하여 나타낼 수 있습니다.
사인 코사인 접선 코탄젠트 쌍각공식[25] [26] 죄악의 ( 2 θ ) = 2 죄악의 θ cos θ = 2 태닝한 θ 1 + 태닝한 2 θ {\displaystyle {\begin{aligned}\sin(2\theta)&=2\sin \theta \cos \theta \&={\frac {2\tan \theta}{1+\tan^{2}\theta}}\end{aligned}} cos ( 2 θ ) = cos 2 θ − 죄악의 2 θ = 2 cos 2 θ − 1 = 1 − 2 죄악의 2 θ = 1 − 태닝한 2 θ 1 + 태닝한 2 θ {\displaystyle {\begin{aligned}\cos(2\theta)&=\cos ^{2}\theta -\sin ^{2}\theta \&=2\cos ^{2}\theta -1\&=1-2\sin ^{2}\theta \&={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}\end{aligned}} 태닝한 ( 2 θ ) = 2 태닝한 θ 1 − 태닝한 2 θ {\displaystyle \tan(2\theta)={\frac {2\tan \theta}{1-\tan^{2}\theta}}} 간이 침대 ( 2 θ ) = 간이 침대 2 θ − 1 2 간이 침대 θ {\displaystyle \cot(2\theta)={\frac {\cot^{2}\theta -1}{2\cot \theta}}} 삼중각 공식[18] [27] 죄악의 ( 3 θ ) = − 죄악의 3 θ + 3 cos 2 θ 죄악의 θ = − 4 죄악의 3 θ + 3 죄악의 θ {\displaystyle {\begin{aligned}\sin(3\theta)&=-\sin^{3}\theta +3\cos ^{2}\theta \sin \theta \&=-4\sin^{3}\theta +3\sin \end{aligned}} cos ( 3 θ ) = cos 3 θ − 3 죄악의 2 θ cos θ = 4 cos 3 θ − 3 cos θ {\displaystyle {\begin{aligned}\cos(3\theta)&=\cos ^{3}\theta -3\sin ^{2}\theta \cos \theta \&=4\cos ^{3}\theta -3\cos \end{aligned}} 태닝한 ( 3 θ ) = 3 태닝한 θ − 태닝한 3 θ 1 − 3 태닝한 2 θ {\displaystyle \tan(3\theta )={\frac {3\tan \theta -\tan^{3}\theta}{1-3\tan^{2}\theta}} 간이 침대 ( 3 θ ) = 3 간이 침대 θ − 간이 침대 3 θ 1 − 3 간이 침대 2 θ {\displaystyle \cot(3\theta)={\frac {3\cot \theta -\cot ^{3}\theta}{1-3\cot ^{2}\theta}} 반각공식[23] [24] 죄악의 θ 2 = sgn ( 죄악의 θ 2 ) 1 − cos θ 2 ( 아니면 죄악의 2 θ 2 = 1 − cos θ 2 ) {\displaystyle {\begin{aligned}&\sin {\frac {\theta}{2}}=\operatorname {sgn} \left(\sin {\frac {\theta}{2}}\right){\sqrt {\frac {1-\cos \theta}{2}}\\\\\left ({\text{or}}\sin^{2}{\frac {1-\cos \theta}{2}\right)\end{aligned}} cos θ 2 = sgn ( cos θ 2 ) 1 + cos θ 2 ( 아니면 cos 2 θ 2 = 1 + cos θ 2 ) {\displaystyle {\begin{aligned}&\cos {\theta}{2}}=\operatorname {sgn} \left(\cos {\frac {\theta}{2}}\right){\sqrt {\frac {1+\cos \theta}{2}}\\\&\left ({\text{or}}\cos^{2}{\frac {\theta}{2}}={\frac {1+\cos \theta}{2}\right)\end{aligned}} 태닝한 θ 2 = csc θ − 간이 침대 θ = ± 1 − cos θ 1 + cos θ = 죄악의 θ 1 + cos θ = 1 − cos θ 죄악의 θ 태닝한 η + θ 2 = 죄악의 η + 죄악의 θ cos η + cos θ 태닝한 ( θ 2 + π 4 ) = 초 θ + 태닝한 θ 1 − 죄악의 θ 1 + 죄악의 θ = 1 − 태닝한 θ 2 1 + 태닝한 θ 2 태닝한 θ 2 = 태닝한 θ 1 + 1 + 태닝한 2 θ 위해서 θ ∈ ( − π 2 , π 2 ) {\displaystyle {\begin{aligned}\tan {\frac {\theta}{2}}&=\csc \theta -\cot \theta \,{\sqrt {\frac {1-\cos \theta}{1+\cos \theta}}\[3pt]&={\frac {\sin \theta}{1+\cos \theta}}\[3pt]&={\frac {1-\cos \theta}{\sin \theta}}\[5pt]\tan {\frac {\eta +\theta}{2}}&={\frac {\sin \eta +\sin \theta }}\[5pt]\tan \left \tan ({\frac {\theta}{2}}+{\frac {\pi}{4}}\right)&=\sec \theta +\tan \theta \[5pt]{\sqrt {\frac {1-\sin \theta}{1+\sin \theta}}&={\frac {\left 1-\tan {\frac {\theta}{2}}\right }}{\left 1+\tan {\frac {\theta}{2}}}\[5pt]\tan {\frac {\theta}{2}}}&={\frac {\tan \theta}{1+{\sqrt {1+\tan ^{2}}}}\&\&{\text{fra}\left (- {\tfra}}\tfra. c {\pi}{2}},{\tfrac {\pi}{2}}\right)\end{aligned}} 간이 침대 θ 2 = csc θ + 간이 침대 θ = ± 1 + cos θ 1 − cos θ = 죄악의 θ 1 − cos θ = 1 + cos θ 죄악의 θ {\디스플레이 스타일 {\begin{aligned}\cot {\frac {\theta}{2}}&=\csc \theta +\cot \theta \&=\pm \,{\sqrt {\frac {1+\cos \theta}{1-\cos \theta}}\[3pt]&={\frac {\sin \theta}{1-\cos \theta}}\[4pt]&={\frac {1+\cos \theta}{\sin \theta}}\end{aligned}}
사인과 코사인에 대한 삼중각 공식이 단지 단일 함수의 거듭제곱만을 포함한다는 사실은 나침반 의 기하학적 문제와 각도 분할 의 직선적인 구성 을 주어진 도구를 사용하여 분할이 일반적으로 불가능하다는 것을 증명할 수 있는 입방정식 을 푸는 대수적 문제와 관련시킬 수 있게 해줍니다. 장론으로 [citation needed
1/3 각도에 대한 삼각형 항등식을 계산하는 공식이 존재하지만, 3차 방정식 4x - 3x + d 0 의 영점을 찾아야 하며, 여기서 x {\displaystyle x} d 는 전체 각도에서 코사인 함수의 알려진 값입니다. 그러나 이 방정식의 판별 은 양이므로 이 방정식에는 3개의 실제 근이 있습니다(그 중 1개만 1/3 각도의 코사인에 대한 해입니다). 이 해들 중 어떤 것 도 세제곱근 아래의 중간 복소수를 사용하기 때문에 실제 대수적 표현 으로 축소 할 수 없습니다.
전력 감소 공식 코사인 이중각 공식의 두 번째 버전과 세 번째 버전을 풀어서 얻은 것.
사인 코사인 다른. 죄악의 2 θ = 1 − cos ( 2 θ ) 2 {\displaystyle \sin ^{2}\theta = {\frac {1-\cos(2\theta )}{2}}} cos 2 θ = 1 + cos ( 2 θ ) 2 {\displaystyle \cos ^{2}\theta = {\frac {1+\cos(2\theta )}{2}}} 죄악의 2 θ cos 2 θ = 1 − cos ( 4 θ ) 8 {\displaystyle \sin ^{2}\theta \cos ^{2}\theta = {\frac {1-\cos(4\theta)}{8}} 죄악의 3 θ = 3 죄악의 θ − 죄악의 ( 3 θ ) 4 {\displaystyle \sin ^{3}\theta = {\frac {3\sin \theta -\sin(3\theta )}{4}} cos 3 θ = 3 cos θ + cos ( 3 θ ) 4 {\displaystyle \cos ^{3}\theta = {\frac {3\cos \theta +\cos(3\theta )}{4}} 죄악의 3 θ cos 3 θ = 3 죄악의 ( 2 θ ) − 죄악의 ( 6 θ ) 32 {\displaystyle \sin ^{3}\theta \cos ^{3}\theta = {\frac {3\sin(2\theta)-\sin(6\theta)}{32}} 죄악의 4 θ = 3 − 4 cos ( 2 θ ) + cos ( 4 θ ) 8 {\displaystyle \sin ^{4}\theta = {\frac {3-4\cos(2\theta)+\cos(4\theta)}{8}} cos 4 θ = 3 + 4 cos ( 2 θ ) + cos ( 4 θ ) 8 {\displaystyle \cos ^{4}\theta = {\frac {3+4\cos(2\theta)+\cos(4\theta)}{8}} 죄악의 4 θ cos 4 θ = 3 − 4 cos ( 4 θ ) + cos ( 8 θ ) 128 {\displaystyle \sin ^{4}\theta \cos ^{4}\theta = {\frac {3-4\cos(4\theta)+\cos(8\theta)}{128}} 죄악의 5 θ = 10 죄악의 θ − 5 죄악의 ( 3 θ ) + 죄악의 ( 5 θ ) 16 {\displaystyle \sin ^{5}\theta = {\frac {10\sin \theta -5\sin(3\theta)+\sin(5\theta)}{16}} cos 5 θ = 10 cos θ + 5 cos ( 3 θ ) + cos ( 5 θ ) 16 {\displaystyle \cos ^{5}\theta = {\frac {10\cos \theta +5\cos(3\theta) +\cos(5\theta)}{16}} 죄악의 5 θ cos 5 θ = 10 죄악의 ( 2 θ ) − 5 죄악의 ( 6 θ ) + 죄악의 ( 10 θ ) 512 {\displaystyle \sin ^{5}\theta \cos ^{5}\theta = {\frac {10\sin(2\theta)-5\sin(6\theta)+\sin(10\theta)}{ 512}}
코사인 전력 감소 공식: 예시도 빨강, 주황, 파랑 삼각형은 모두 비슷하고 빨강, 주황 삼각형은 합동입니다. 파란색 삼각형의 빗변형 AD {\displaystyle {\overline {AD}} 2코스 {\displaystyle 2\cos \theta} . DAE {\displaystyle \angle DAE} ( {\displaystyle \theta} AE {\overline {AE} 2코스 2 {\displaystyle 2\cos ^{2}\theta} . BD {\displaystyle {\overline }} AF {\displaystyle {\overline {AF}} , 1 코스 ( 2 ) displaystyle +\cos(2\theta )} . 따라서 2 cos 2 1 cos ( 2 ) {\displaystyle 2\cos ^{2}\theta 1+\cos(2\theta )}. 2 . cos displaystyle cos 2}\theta 1 cos 2 {\textstyle {\frac {1}{2}}(1+\cos(2\theta )}. 코사인의 반각 공식은 {\displaystyle \theta } 2 {\displaystyle \theta /2} cos 2 1 cos 2 .{\textstyle \cos \left(\theta 2\right pm {\sqrt left(1+\cos \right)/2}}. 사인 파워-감소 공식: 예시도. 음영처리 된 파란색 및 초록색 삼각형, 빨간색 선이 있는 삼각형 EBD {\displaystyle EBD} {\displaystyle \theta} . BD {\displaystyle {\overline }} 2 sin {\displaystyle 2\sin \theta} DE {\displaystyle e {\overline {DE}} 2 sin 2 θ {\displaystyle 2\sin ^{2}\theta} . AE ¯ {\displaystyle {\overline {AE}} 코스 θ {\displaystyle \cos 2\theta} AE ¯ {\overline {AE}} D ¯ {\displaystyle {\overline {DE} D ¯ {\displaystyle {\overline AD} }}} , 따라서 cos 2 sin 2 1 {\displaystyle \cos 2\theta +2\sin ^{2}\theta 1 양변 cos {\displaystyle \cos \theta . sin 2 {\displaystyle \sin ^{2}\theta 1 2 1 cos 2 )) {\textstyle {\frac {1}{2}}(1-\cos(2\theta))}. 사인의 반각 공식은 {\displaystyle \theta } 2 {\displaystyle \theta /2} sin / 2 cos 2 . textstyle \sin \left(\theta 2\right \pm sqrt left(1-\cos theta )/2 l 라인 세그먼트 EB {\displaystyle {\overline {EB sin 2 sin 코스 {\displaystyle \sin 2\theta 2\sin \theta \cos \theta }.
일반적으로 sin {\displaystyle \sin \theta} cos {\displaystyle \cos \theta} De Moivre 공식, 오일러 공식 및 이항 정리를 사용 하여 추론할 수 있습니다.
n 이 ...일 경우 cos n θ {\displaystyle \cos ^{n}\theta } 죄악의 n θ {\displaystyle \sin ^{n}\theta } n 은 홀수입니다 cos n θ = 2 2 n ∑ k = 0 n − 1 2 ( n k ) cos ( ( n − 2 k ) θ ) {\displaystyle \cos ^{n}\theta = {\frac {2}{2^{n}}\sum _{k=0}^{\frac {n-1}{2}}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}} 죄악의 n θ = 2 2 n ∑ k = 0 n − 1 2 ( − 1 ) ( n − 1 2 − k ) ( n k ) 죄악의 ( ( n − 2 k ) θ ) {\displaystyle \sin ^{n}\theta = {\frac {2}{2^{n}}\sum _{k=0}^{\frac {n-1}{2}}(-1)^{\left ({\frac {n-1}{2}-k\right)}{\binom {n}{k}}\sin {{\big (}(n-2k)\theta {\big )}} n 은 짝수입니다 cos n θ = 1 2 n ( n n 2 ) + 2 2 n ∑ k = 0 n 2 − 1 ( n k ) cos ( ( n − 2 k ) θ ) {\displaystyle \cos ^{n}\theta = {\frac {1}{2^{n}}{\binom {n}{\frac {n}}+{\frac {2}{2^{n}}\sum _{k=0}^{{\frac {n}{2}}-1}{\binom {n}{k}}\cos {\big(}(n-2k)\theta {\big)}} 죄악의 n θ = 1 2 n ( n n 2 ) + 2 2 n ∑ k = 0 n 2 − 1 ( − 1 ) ( n 2 − k ) ( n k ) cos ( ( n − 2 k ) θ ) {\displaystyle \sin ^{n}\theta = {\frac {1}{2^{n}}{\binom {n}{\frac {n}}+{\frac {2}}+{\frac {2}}-1}(-1)^{\left ({\frac {n}{2}}-k\right)}{\binom {n}{k}}\cos {{n-2k}\theta {\big}}}
제품 대 제품 및 제품 대 제품 ID 곱 대 합 항등식[28] 전립선 공식은 각도 덧셈 정리 를 사용하여 오른쪽 측면을 확장함으로써 증명할 수 있습니다. 역사적으로, 이들 중 처음 네 개는 천문학적 계산을 위해 그것들을 사용한 요하네스 베르너 의 이름을 따서 베르너의 공식 으로 알려져 있습니다.[29] 곱 대 곱 공식의 적용에 대해서 는 진폭 변조 를, 합 대 곱 공식의 적용 에 대해서는 비트(음향) 와 위상 검출기 를 참조합니다.
제품 대 합 ID cos θ cos φ = cos ( θ − φ ) + cos ( θ + φ ) 2 {\display style \cos \theta \,\cos \varphi = {\cos(\theta -\varphi )+\cos(\theta +\varphi ) \over 2} 죄악의 θ 죄악의 φ = cos ( θ − φ ) − cos ( θ + φ ) 2 {\displaystyle \sin \theta \,\sin \varphi = {\cos(\theta -\varphi )-\cos(\theta +\varphi ) \over 2} 죄악의 θ cos φ = 죄악의 ( θ + φ ) + 죄악의 ( θ − φ ) 2 {\displaystyle \sin \theta \,\cos \varphi = {\sin(\theta +\varphi )+\sin(\theta -\varphi ) \over 2} cos θ 죄악의 φ = 죄악의 ( θ + φ ) − 죄악의 ( θ − φ ) 2 {\displaystyle \cos \theta \,\sin \varphi = {\sin(\theta +\varphi )-\sin(\theta -\varphi ) \over 2} 태닝한 θ 태닝한 φ = cos ( θ − φ ) − cos ( θ + φ ) cos ( θ − φ ) + cos ( θ + φ ) {\displaystyle \tan \theta \,\tan \varphi ={\frac {\cos(\theta -\varphi )-\cos(\theta +\varphi )}{\cos(\theta -\varphi )+\cos(\theta +\varphi )}} 태닝한 θ 간이 침대 φ = 죄악의 ( θ + φ ) + 죄악의 ( θ − φ ) 죄악의 ( θ + φ ) − 죄악의 ( θ − φ ) {\displaystyle \tan \theta \,\cot \varphi ={\frac {\sin(\theta +\varphi )+\sin(\theta -\varphi )}{\sin(\theta +\varphi )-\sin(\theta -\varphi )}} ∏ k = 1 n cos θ k = 1 2 n ∑ e ∈ S cos ( e 1 θ 1 + ⋯ + e n θ n ) 어디에 e = ( e 1 , ⋯ , e n ) ∈ S = { 1 , − 1 } n {\displaystyle {\begin{aligned}\prod _{k=1}^{n}\cos \theta _{k}&={\frac {1}{2^{n}}}\sum _{e\in S}\cos(e_{1}\cdots +e_{n}\theta _{n})\[6pt]&{text{{where }}\e=(e_{1},\cdots,e_{n})\in S=\{1,-1\}^{n}\end{aligned}}} ∏ k = 1 n 죄악의 θ k = ( − 1 ) ⌊ n 2 ⌋ 2 n { ∑ e ∈ S cos ( e 1 θ 1 + ⋯ + e n θ n ) ∏ j = 1 n e j 한다면 n 짝수다 , ∑ e ∈ S 죄악의 ( e 1 θ 1 + ⋯ + e n θ n ) ∏ j = 1 n e j 한다면 n 기묘한 {\displaystyle \prod _{k=1}^{n}\sin \theta _{k}={\frac {(-1)^{\left\l floor {\frac {n}{2}}\right\rfloor }}{{2^{n}}\displaystyle \sum _{e\in S}\cos(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n}\deta _{j=1}^{n}\;{\text{if}}\n;{\text{iseven}}}, \\\displaystyle \sum _{e\in S}\sin(e_{1})\theta _{1}+\cdots +e_{n}\theta _{n})\prod _{j=1}^{n}e_{j}\;{\text{if}}\;{\text{is odd}}\end{case}} Sum-to-Product ID 사인 및 코사인에 대한 제품 간 합 식별을 보여주는 다이어그램입니다. 파란색 직각삼각형은 각도 θ {\displaystyle \theta} {\displaystyle \varphi} . 여기서 p {\displaystyle p} q {\displaystyle q} p ) {\displaystyle theta +\varphi )/2} q ( ) {\displaystyle theta \varphi )/2} . q {\displaystyle \theta p+q} q {\displaystyle \varphi p-q} . 구성할 rple-outline 삼각형 AFG {\displaystyle AFG} FCE {\displaystyle FCE} q displaystyle cosq} p {\displaystyle p} 빨간색 삼각형과 파란색 삼각형 sin sin displaystyle sin \theta +\sin varphi} , , sin p cos q {\displaystyle \sin p\cos q} q {\displaystyle q} {\displaystyle theta {\displaystyle \varphi } s in θ s in φ = s i n θ φ 2 )코 스 ( 2 ){\displaystyle \sin \theta +\sin \varp h i 2\sin \le ft frac {\theta +\varphi }{2}\right)\cos \le ft frac {\theta \varphi }{2}\right)} 빨간색 삼각형과 파란색 삼각형의 너비의 합은 코사인에 해당하는 항등식을 산출합니다. 제품 간 합 식별 정보는 다음과 같습니다.[30]
죄악의 θ ± 죄악의 φ = 2 죄악의 ( θ ± φ 2 ) cos ( θ ∓ φ 2 ) {\displaystyle \sin \theta \pm \sin \varphi = 2\sin \left ({\frac {\theta \pm \varphi }{2}}\right)\cos \left ({\frac {\theta \mp \varphi }{2}\right)} cos θ + cos φ = 2 cos ( θ + φ 2 ) cos ( θ − φ 2 ) {\displaystyle \cos \cos \theta +\cos \varphi =2\cos \left ({\frac {\theta +\varphi }{2}}\right)\cos \left ({\frac {\theta -\varphi }{2}\right)} cos θ − cos φ = − 2 죄악의 ( θ + φ 2 ) 죄악의 ( θ − φ 2 ) {\displaystyle \cos \cos \theta -\cos \varphi =-2\sin \left ({\frac {\theta +\varphi }{2}}\right)\sin \left ({\frac {\theta -\varphi }{2}\right)} 태닝한 θ ± 태닝한 φ = 죄악의 ( θ ± φ ) cos θ cos φ {\display style \tan \theta \pm \tan \varphi ={\frac {\sin(\theta \pm \varphi )}{\cos \theta \,\cos \varphi }} 헤르마이트의 동분서주하는 정체성 찰스 헤르마이트 는 다음과 같은 정체성을 보여주었습니다.[31] 1 , …, {\displaystyle a_{1},\ldots,a_{n}} 복소수 이고, 2개의 개수 가 π의 정수배만큼 다르지 않다고 가정하자.
A n , k = ∏ 1 ≤ j ≤ n j ≠ k 간이 침대 ( a k − a j ) {\displaystyle A_{n,k}=\prod _{\begin{smallmatrix}1\leq j\leq n\j\neq k\end{smallmatrix}}\cot(a_{k}-a_{j})}
(특히 A 1, 1 {\displaystyle A_{1,1}} 제품 입니다.) 그리고나서
간이 침대 ( z − a 1 ) ⋯ 간이 침대 ( z − a n ) = cos n π 2 + ∑ k = 1 n A n , k 간이 침대 ( z − a k ) . {\displaystyle \cot(z-a_{1})\cdots \cot(z-a_{n})=\cos {\frac {n\pi}{2}}+\sum _{k=1}^{n}A_{n,k}\cot(z-a_{k})}
가장 간단한 비 trivial 예는 n 2 인 경우입니다.
간이 침대 ( z − a 1 ) 간이 침대 ( z − a 2 ) = − 1 + 간이 침대 ( a 1 − a 2 ) 간이 침대 ( z − a 1 ) + 간이 침대 ( a 2 − a 1 ) 간이 침대 ( z − a 2 ) . {\displaystyle \cot(z-a_{1})\cot(z-a_{2})=-1+\cot(a_{1}-a_{2})\cot(z-a_{1})+\cot(a_{2}-a_{1})\cot(z-a_{2})}
삼각함수의 유한곱 공임계 정수 n , m
∏ k = 1 n ( 2 a + 2 cos ( 2 π k m n + x ) ) = 2 ( T n ( a ) + ( − 1 ) n + m cos ( n x ) ) {\displaystyle \prod _{k=1}^{n}\left(2a+2\cos \left ({\frac {2\pi km}{n}}+x\right)\right)=2\left(T_{n}(a)+{(-1)}^{n+m}\cos(nx)\right)}
여기서 T 는n 체비셰프 다항식 입니다.
사인 함수에 대해 다음 관계가 성립합니다.
∏ k = 1 n − 1 죄악의 ( k π n ) = n 2 n − 1 . {\displaystyle \prod _{k=1}^{n-1}\sin \left ({\frac {k\pi}{n}}\right)={\frac {n}{2^{n-1}}}}
일반적으로 정수 0 의[32]
죄악의 ( n x ) = 2 n − 1 ∏ k = 0 n − 1 죄악의 ( k n π + x ) = 2 n − 1 ∏ k = 1 n 죄악의 ( k n π − x ) . {\displaystyle \sin(nx)=2^{n-1}\prod _{k=0}^{n-1}\sin \left ({\frac {k}{n}}\pi +x\right)=2^{n-1}\sin \left ({\frac {k}{n}\pi -x\right).}
또는 코드 함수 crd x sin 12 x {\textstyle \operatorname {crd} x\equiv 2\sin {\tfrac {1}{2} x
crd ( n x ) = ∏ k = 1 n crd ( k n 2 π − x ) . {\displaystyle \operatorname {crd}(nx)=\prod _{k=1}^{n}\operatorname {crd} \left ({\frac {k}{n}}2\pi -x\right)}
이것은 다항식 z n 1 {\textstyle z^{n}-1} 일치의 루트 )로인수분해하는 것에서 비롯됩니다. 복소수 단위 원 위의 점 z 와 정수 0 에 대하여,
z n − 1 = ∏ k = 1 n z − 익스피드 ( k n 2 π i ) . {\displaystyle z^{n}-1=\prod _{k=1}^{n}z-\exp {\Bigl(}{\frac {k}{n}}}2\pi i{\Bigr}}}
선형결합 어떤 목적에서는 주기나 주파수는 같지만 위상 이동 이 다른 사인파의 선형 조합도 주기나 주파수는 같지만 위상 이동은 다른 사인파임을 알아야 합니다. 이는 측정되거나 관측된 데이터가 아래의 동상 및 직교 성분 기반 의 a 및 b 미지와 선형적으로 연관되어 c {\displaystyle c} {\displaystyle \varphi} 자코비안 을 생성하기 때문에 동축 데이터 피팅 에 유용합니다.
사인과 코사인 사인파와 코사인파의 선형 조합 또는 고조파 덧셈은 위상 이동 및 크기 조정 진폭이 있는 단일 사인파와 동일합니다.[33] [34]
a cos x + b 죄악의 x = c cos ( x + φ ) {\displaystyle a\cos x+b\sin x=c\cos(x+\varphi )}
여기서 c {\displaystyle c} {\displaystyle \varphi}
c = sgn ( a ) a 2 + b 2 , φ = 아크탄 ( − b a ) , {\displaystyle {\begin{aligned}c&=\operatorname {sgn}(a){\sqrt {a^{2}+b^{2} }},\\varphi &=\arctan \left (-{\frac {b}{a}\right}),\end{aligned}}
≠ {\displaystyle neq .} 주어지면
임의 위상 변이 일반적으로 임의의 위상 이동에 대해
a 죄악의 ( x + θ a ) + b 죄악의 ( x + θ b ) = c 죄악의 ( x + φ ) {\displaystyle a\sin(x+\theta _{a})+b\sin(x+\theta _{b})=c\sin(x+\varphi )}
여기서 c {\displaystyle c} {\displaystyle \varphi}
c 2 = a 2 + b 2 + 2 a b cos ( θ a − θ b ) , 태닝한 φ = a 죄악의 θ a + b 죄악의 θ b a cos θ a + b cos θ b . {\디스플레이 스타일 {\begin{aligned}c^{2}&=a^{2}+b^{2}+2ab\cos \left(\theta _{a}-\theta _{b}\right),\\tan \varphi &={\frac {a\sin \theta _{a}+b\sin \theta _{b}}{a\cos \theta _{b}}}. \end{aligned}}
2개 이상의 정현파 일반적인 경우는[34]
∑ i a i 죄악의 ( x + θ i ) = a 죄악의 ( x + θ ) , {\displaystyle \sum _{i}a_{i}\sin(x+\theta _{i})=a\sin(x+\theta),} 어디에 a 2 = ∑ i , j a i a j cos ( θ i − θ j ) {\displaystyle a^{2}=\sum _{i,j}a_{i}a_{j}\cos(\theta _{i}-\theta _{j})} 그리고. 태닝한 θ = ∑ i a i 죄악의 θ i ∑ i a i cos θ i . {\displaystyle \tan \theta = {\frac {\sum _{i}a_{i}\sin \theta _{i}}{\sum _{i}a_{i}\cos \theta _{i}}}
라그랑주의 삼각형 항등식 조지프 루이스 라그랑주 의 이름을 딴 이 신원들은 다음과 같습니다.[35] [36] [37]
∑ k = 0 n 죄악의 k θ = cos 1 2 θ − cos ( ( n + 1 2 ) θ ) 2 죄악의 1 2 θ ∑ k = 0 n cos k θ = 죄악의 1 2 θ + 죄악의 ( ( n + 1 2 ) θ ) 2 죄악의 1 2 θ {\displaystyle {\begin{aligned}\sum _{k=0}^{n}\sin k\theta &={\frac {1}{2}}\theta -\cos \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\[5pt]\sum _{k=0}^{n}\cos k\theta &={\sin {\tfrac {1}{2}}\theta +\sin \left(n+{\tfrac {1}{2}\right)}{2}}\theta \right)}{2\sin {\tfrac {1}{2}}\theta \right)}{2\sin {\tfrac {1}}}\theta }}\end{aligned}} θ ≢ 0 mod ) .{\displaystyle theta not \equiv 0{\pmod \pi}}}.
이와 관련된 함수로는 디리클레 커널 이 있습니다.
D n ( θ ) = 1 + 2 ∑ k = 1 n cos k θ = 죄악의 ( ( n + 1 2 ) θ ) 죄악의 1 2 θ . {\displaystyle D_{n}(\theta )=1+2\sum _{k=1}^{n}\cos k\theta ={\frac {\sin \left(n+{\tfrac {1}{2}}\right)\theta \right) }{\sin {\tfrac {1}{2}}\theta}}}.
비슷한 정체성은[38]
∑ k = 1 n cos ( 2 k − 1 ) α = 죄악의 ( 2 n α ) 2 죄악의 α . {\displaystyle \sum _{k=1}^{n}\cos(2k-1)\alpha = {\frac {\sin(2n\alpha)}{2\sin \alpha}}}
그 증거는 다음과 같습니다. 각도 합 과 차 항등식 을 이용하여
죄악의 ( A + B ) − 죄악의 ( A − B ) = 2 cos A 죄악의 B . {\displaystyle \sin(A+B)-\sin(A-B)=2\cos A\sin B.} 그렇다면 다음의 공식을 살펴보도록 하겠습니다.
2 죄악의 α ∑ k = 1 n cos ( 2 k − 1 ) α = 2 죄악의 α cos α + 2 죄악의 α cos 3 α + 2 죄악의 α cos 5 α + … + 2 죄악의 α cos ( 2 n − 1 ) α {\displaystyle 2\sin \alpha \sum _{k=1}^{n}\cos(2k-1)\alpha = 2\sin \alpha \cos \alpha +2\sin \alpha \cos 3\alpha +2\sin \alpha \cos 5\alpha +\ldots +2\sin \alpha \cos(2n-1)\alpha } 그리고 이 공식은 위의 신원을 이용하여 작성될 수 있고,
2 죄악의 α ∑ k = 1 n cos ( 2 k − 1 ) α = ∑ k = 1 n ( 죄악의 ( 2 k α ) − 죄악의 ( 2 ( k − 1 ) α ) ) = ( 죄악의 2 α − 죄악의 0 ) + ( 죄악의 4 α − 죄악의 2 α ) + ( 죄악의 6 α − 죄악의 4 α ) + … + ( 죄악의 ( 2 n α ) − 죄악의 ( 2 ( n − 1 ) α ) ) = 죄악의 ( 2 n α ) . {\displaystyle {\begin{aligned}&2\sin \alpha \sum _{k=1}^{n}\cos(2k-1)\alpha \&\quad =\sum _{k=1}^{n}(\sin(2k\alpha )-\sin(2(k-1))\&\quad =(\sin 2\alpha -\sin 0)+(\sin 4\alpha )+(\sin 6\alpha -\sin 4\alpha )+(\sin 6\alpha )+(\sin(2n\alpha )-\sin(2n-1)\sin(2n\alpha )+&\sin(2n\alpha )=\sin(2n\alpha )+(\sin 6\alpha )+(\sin 6\alpha )+(\sin 4\alpha )+(\sin(2n\alpha )+(\sin)+(\sin(2n\alpha )+(\sin)+(\sin(2n)+(\sin)+(\sin(2n)+ \end{aligned}}
따라서 이 공식을 2 sin α {\displaystyle 2\sin \alpha}
특정 선형 분수 변환 f x ) {\displaystyle f(x)} 선형 에 의해 주어졌을 경우
f ( x ) = ( cos α ) x − 죄악의 α ( 죄악의 α ) x + cos α , {\displaystyle f(x)={\frac {(\cos \alpha)x-\sin \alpha}{(\sin \alpha)x+\cos \alpha}}},} 마찬가지로 g ( x ) = ( cos β ) x − 죄악의 β ( 죄악의 β ) x + cos β , {\displaystyle g(x)={\frac {(\cos \beta)x-\sin \beta }{(\sin \beta)x+\cos \beta }}},} 그리고나서 f ( g ( x ) ) = g ( f ( x ) ) = ( cos ( α + β ) ) x − 죄악의 ( α + β ) ( 죄악의 ( α + β ) ) x + cos ( α + β ) . {\displaystyle f{\big (}g(x)){\big )}=g{\big (}f(x){\big )}={\frac {{\big (}\cos(\alpha +\beta ){\big )}{{\big (}\big )}{\big (}\sin(\alpha +\beta ){\big )}{x+\cos(\alpha +\beta )}}
좀 더 간단히 말하면, 모든 α {\displaystyle \alpha} {\ displaystyle f_{\alpha}} f {\displaystyle f}
f α ∘ f β = f α + β . {\displaystyle f_{\alpha}\circ f_{\beta }=f_{\alpha +\beta }}
x {\displaystyle x} ( x ) {\displaystyle f(x)} -α . {\displaystyle \alpha.}
복소수 지수 함수와의 관계 오일러 공식은 임의의 실수 x 에 대하여 다음과 같이 말합니다.[39]
e i x = cos x + i 죄악의 x , {\displaystyle e^{ix}=\cos x+i\sin x,} 여기서 i 는 상상의 단위 입니다. -x를 x 에 대입하면 다음과 같은 결과가 나옵니다. e − i x = cos ( − x ) + i 죄악의 ( − x ) = cos x − i 죄악의 x . {\displaystyle e^{-ix}=\cos (-x)+i\sin (-x)=\cos x-i\sin x.}
이 두 방정식은 지수 함수 의 관점에서 코사인과 사인에 대한 풀이에 사용될 수 있습니다. 구체적으로.[40] [41]
cos x = e i x + e − i x 2 {\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}}} 죄악의 x = e i x − e − i x 2 i {\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}}}
이 공식들은 다른 많은 삼각형 항등식을 증명하는 데 유용합니다. 예를 들어, e e
cos(θ + φ) + isin(θ + φ ) = (cos θ + is in θ) (cos θ + is in φ) = (cos φ 코스 φ - sin φ sin θ) + i cos θ sin φ + sin θ 코스 φ).
좌변의 실수 부분이 우변의 실수 부분과 같다는 것은 코사인의 각도 덧셈 공식입니다. 허수 부품의 동일성은 사인에 대한 각도 덧셈 공식을 제공합니다.
다음 표는 삼각 함수와 그 역수를 지수 함수와 복소수 로그 로 표현한 것입니다.
기능. 역함수[42] 죄악의 θ = e i θ − e − i θ 2 i {\displaystyle \sin \theta = {\frac {e^{i\theta}}-e^{-i\theta}}{2i}} 호신 x = − i ln ( i x + 1 − x 2 ) {\displaystyle \arcsin x=-i\,\ln \left(ix+{\sqrt {1-x^{2}}}\right)} cos θ = e i θ + e − i θ 2 {\displaystyle \cos \theta = {\frac {e^{i\theta}+e^{-i\theta}}{2}} 아코코 x = − i ln ( x + x 2 − 1 ) {\displaystyle \arccos x=-i\,\ln \left(x+\,{\sqrt {x^{2}-1}}\right)} 태닝한 θ = − i e i θ − e − i θ e i θ + e − i θ {\displaystyle \tan \theta =-i\,{\frac {e^{i\theta}-e^{-i\theta}}}{e^{i\theta}}}{e^{i\theta}}} 아크탄 x = i 2 ln ( i + x i − x ) {\displaystyle \arctan x={\frac {i}{2}}\ln \left ({\frac {i+x}{i-x}}\right)} csc θ = 2 i e i θ − e − i θ {\displaystyle \csc \theta = {\frac {2i}{e^{i\theta}-e^{-i\theta}}}}} arccsc x = − i ln ( i x + 1 − 1 x 2 ) {\displaystyle \operatorname {arccsc} x=-i\,\ln \left ({\frac {i}{x}}+{\sqrt {1-{\frac {1}{x^{2}}}\right)} 초 θ = 2 e i θ + e − i θ {\displaystyle \sec \theta = {\frac {2}{e^{i\theta}+e^{-i\theta}}}}개 아크섹 x = − i ln ( 1 x + i 1 − 1 x 2 ) {\displaystyle \operatorname {arcsec} x=-i\,\ln \left ({\frac {1}{x}}+i{\sqrt {1-{\frac {1}{x^{2}}}\right)} 간이 침대 θ = i e i θ + e − i θ e i θ − e − i θ {\displaystyle \cot \theta =i\,{\frac {e^{i\theta}+e^{-i\theta}}}{e^{i\theta}}}{e^{-i\theta}}} 아궁이 x = i 2 ln ( x − i x + i ) {\displaystyle \operatorname {arccot} x={\frac {i}{2}\ln \left ({\frac {x-i}{x+i}\right)} 시스 θ = e i θ {\displaystyle \operator name {cis} \theta =e^{i\theta}} 아크시스 x = − i ln x {\displaystyle \operator name {arccis} x=-i\ln x}
무한곱 공식 특수 함수 에 적용할 경우 삼각 함수에 대한 다음과 같은 무한 곱 공식 이 유용합니다.[43] [44]
죄악의 x = x ∏ n = 1 ∞ ( 1 − x 2 π 2 n 2 ) cos x = ∏ n = 1 ∞ ( 1 − x 2 π 2 ( n − 1 2 ) 2 ) 죄스러운 x = x ∏ n = 1 ∞ ( 1 + x 2 π 2 n 2 ) 으스스한 x = ∏ n = 1 ∞ ( 1 + x 2 π 2 ( n − 1 2 ) 2 ) {\displaystyle {\begin{aligned}\sin x&=x\prod _{n=1}^{\infty}}\left(1-{\frac {x^{2}}{\pi ^{2}^{2}}\right)&\cos x&=\prod _{n=1}^{\infty}\left(1-{\frac {x^{2}}{\pi ^{2}}\left(n-{\frac {1}{2}}\right)^{2}\right)}\left(n-{\frac {2}}\right) \\\sinh x&=x\prod _{n=1}^{\infty}}\left(1+{\frac {x^{2}}{\pi ^{2}}\right)&\cosh x&=\prod _{n=1}^{\infty}\left(1+{\frac {x^{2}}{\pi ^{2}}\left(n-{\frac {1}{2}}\right)^{2}}\right)\end{aligned}}
무한합 항등식 ∑ k 1 k ln 1 {\displaystyle \sum _{k 1}^{\infty }{\frac {x^{k}}} -\ln( 1-x )} x e it displaystyle x pm } .
∑ k = 1 ∞ cos k t k = − 1 2 ln ( 2 − 2 cos t ) ∑ k = 1 ∞ 죄악의 k t k = π − t 2 {\displaystyle \sum _{k=1}^{\infty}{\frac {\coskt}}=-{\frac {1}{2}}\ln(2-2\cost t)\quad \sum _{k=1}^{\infty}{\frac {\sinkt}}={\frac {\pi -t}{2}} fort 0 , 2 displaystyle t\in [0,2\pi ]}. 주기적 displaystyle pi } {\displaystyle t} ∑ k = 1 ∞ 죄악의 k t k 2 = − 1 2 ∫ 0 t ln ( 2 − 2 cos x ) d x ∑ k = 1 ∞ cos k t k 2 = π 2 6 − π t 2 + t 2 4 {\displaystyle \sum _{k=1}^{\infty}{\frac {\sinkt}{k^{2}}=-{\frac {1}{2}}\int _{0}^{t}\ln(2-2\cos x) dx\quad \sum _{k=1}^{\infty }{\frac {\cos kt}{k^{2}}={\frac {\pi ^2}}{6}}-{\frac {\pi t}{2}}+{\frac {t^{2}}{4}}} 등등.
역삼각함수 다음의 항등식은 역삼각형 함수로 삼각형 함수를 구성한 결과를 제공합니다.[45]
죄악의 ( 호신 x ) = x cos ( 호신 x ) = 1 − x 2 태닝한 ( 호신 x ) = x 1 − x 2 죄악의 ( 아코코 x ) = 1 − x 2 cos ( 아코코 x ) = x 태닝한 ( 아코코 x ) = 1 − x 2 x 죄악의 ( 아크탄 x ) = x 1 + x 2 cos ( 아크탄 x ) = 1 1 + x 2 태닝한 ( 아크탄 x ) = x 죄악의 ( arccsc x ) = 1 x cos ( arccsc x ) = x 2 − 1 x 태닝한 ( arccsc x ) = 1 x 2 − 1 죄악의 ( 아크섹 x ) = x 2 − 1 x cos ( 아크섹 x ) = 1 x 태닝한 ( 아크섹 x ) = x 2 − 1 죄악의 ( 아궁이 x ) = 1 1 + x 2 cos ( 아궁이 x ) = x 1 + x 2 태닝한 ( 아궁이 x ) = 1 x {\displaystyle {\begin{aligned}\sin(\arcsin x)&=x&\cos(\arcsin x)&={\sqrt {1-x^{2}}&\tan(\arcsin x)&={\frac {x}{\sqrt {1-x^{2}}}&\sin(\arccos x)&={\sqrt {1-x^{2}}&\cos(\arccos x)&={\frac {\sqrt {1-x^{2}}&={\sqrt {x}}\sin(\arctan x)&={\frac {x}{\sqrt {1+x^{2}}}&{{\frac {x}{\sqrt {x}}{\sqrt {1+x}}{2}}&\sqrt {x}} }}}}&\cos(\arctan x)&={\frac {1}{\sqrt {1+x^{2 }}}&\tan(\arctan x)&=x\\sin(\operatorname {arccsc} x)&={\frac {1}{x}}&\cos(\operatorname {arccsc} x)&={\frac {\sqrt {x^{2}-1}}&\tan(\operatorname {arccsc} x)&={\frac {1}{\sqrt {x^{2}-1}}\\sin(\operatorname {arcsec} x)&={\frac {\sqrt {x^{2}-1}}&\cos(\operatorname {arcsec} x)&={\frac {1}{x}}&\tan(\operatorname {arcsec} x)&={\sqrt {x^{2}-1}}&\sqrt {arcsec}-. 1}}\\\sin(\operator name {arccot} x)&={\frac {1}{\sqrt {1+x^{2 }}}}&\cos(\operator name {arccot} x)&={\frac {x}{\sqrt {1+x^{2 }}}:&\tan(\operator name {arccot} x)&={\frac {1}{x}}\\end{aligned}}
위의 각 방정식의 양변의 곱셈 역 을 취하면 csc 1 sin sec cos cot tan . {\displaystyle \csc frac {1}{\sin}},\;\sec frac {1}{\cos {\text{ and }},\cot frac {1}{\tan}}}. 예를 들어 cot ( x {\displaystyle \cot(\arcsin )}
간이 침대 ( 호신 x ) = 1 태닝한 ( 호신 x ) = 1 x 1 − x 2 = 1 − x 2 x {\displaystyle \cot(\arcsin x)={\frac {1}{\tan(\arcsin x)}}={\frac {1}{\frac {x}}{\sqrt {1-x^{2}}}={\frac {\sqrt {1-x^{2}}}{x}}}}. csc ( arccos x {\displaystyle \csc(\arccos x)} sec ( arccos x ) {\displaystyle \sec(\arccos x)} csc ( 아코코 x ) = 1 죄악의 ( 아코코 x ) = 1 1 − x 2 그리고. 초 ( 아코코 x ) = 1 cos ( 아코코 x ) = 1 x . {\displaystyle \csc(\arccos x)={\frac {1}{\sin(\arccos x)}}={\frac {1}{\sqrt {1-x^{2}}}}\qquad {\text{ and }}\quad \sec(\arccos x)={\frac {1}{\cos(\arccos x)}={\frac {1}{x}}}.
리플렉션 ID 에는 다음 ID가 포함됩니다.x, r , s , , r , 및 {\displaystyle x, r, s,-x,-r {\text{ }}-s}
π 2 = 호신 ( x ) + 아코코 ( x ) = 아크탄 ( r ) + 아궁이 ( r ) = 아크섹 ( s ) + arccsc ( s ) π = 아코코 ( x ) + 아코코 ( − x ) = 아궁이 ( r ) + 아궁이 ( − r ) = 아크섹 ( s ) + 아크섹 ( − s ) 0 = 호신 ( x ) + 호신 ( − x ) = 아크탄 ( r ) + 아크탄 ( − r ) = arccsc ( s ) + arccsc ( − s ) {\displaystyle {\begin{alignat}{9}{\frac {\pi}{2}}~&=~\arcsin(x)&+\arcos(x)~&=~\arctan(r)&+\operatorname {arcccot}(r)~&=~\operatorname {arcsec}(s)&+\operatorname {arcsc}(s)\[0.4ex]\pi ~=~\arccos(x)&+\arcos (-x)~&=~\operatorname {arccot}(-r)~\operatorname {arcsec}(s)&+\operatorname {arcsec}(-s)\[0.4ex]0 ~&=~\arcsin(x)&+\arcsin (-x)~&=~\arctan(r)&+\arctan (-r)~&=~\operatorname {arcsc}(-s)\[1.0ex]\end{alignat}}
그리고 또.[46]
아크탄 x + 아크탄 1 x = { π 2 , 한다면 x > 0 − π 2 , 한다면 x < 0 아궁이 x + 아궁이 1 x = { π 2 , 한다면 x > 0 3 π 2 , 한다면 x < 0 {\displaystyle {\begin{aligned}\arctan x+\arctan {\dfrac {1}{x}}&={\begin{case}{\frac {\pi}{2}},&{\text{if}}x>0\-{\frac {\pi}{2}},&{\text{if}}x<0\end{case}\\\operatorname {arccot}{\dfrac {1}{x}}&={\text{pi}{2},&{{\text{if}}x>0\frac {3\pi}{2}},&{\text{if}}x<0\end{case}}\\end{aligned}} 아코코 1 x = 아크섹 x 그리고. 아크섹 1 x = 아코코 x {\displaystyle \arccos {\frac {1}{x}}=\operatorname {arcsec} x\qquad {\text{ and }}\qquad \operatorname {arcsec} {\frac {1}{x}}=\arccos x} 호신 1 x = arccsc x 그리고. arccsc 1 x = 호신 x {\displaystyle \arcsin {\frac {1}{x}}=\operatorname {arccsc} x\qquad {\text{ and }}\qquad \operatorname {arccsc} {\frac {1}{x}}=\arcsin x}
아크탄젠트 기능은 다음과 같이 시리즈로 확장할 수 있습니다.[47]
아크탄 ( n x ) = ∑ m = 1 n 아크탄 x 1 + ( m − 1 ) m x 2 {\displaystyle \arctan(nx)=\sum _{m=1}^{n}\arctan {\frac {x}{1+(m-1) mx^{2}}}}
변수가 없는 ID 아크탄젠트 기능에 관해서는 우리가 가지고[46]
아크탄 1 2 = 아크탄 1 3 + 아크탄 1 7 . {\displaystyle \arctan {\frac {1}{2}}=\arctan {\frac {1}{3}}+\arctan {\frac {1}{7}}}
모리의 법칙 으로 알려진 이상한 정체성은
cos 20 ∘ ⋅ cos 40 ∘ ⋅ cos 80 ∘ = 1 8 , {\displaystyle \cos 20^{\circ }\cdot \cos 40^{\circ }\cdot \cos 80^{\circ }={\frac {1}{8}},}
는 하나의 변수를 포함하는 ID의 특수한 경우입니다.
∏ j = 0 k − 1 cos ( 2 j x ) = 죄악의 ( 2 k x ) 2 k 죄악의 x . {\displaystyle \prod _{j=0}^{k-1}\cos \left(2^{j}x\right)={\frac {\sin \left(2^{k}x\right)}{2^{k}\sin x}}}
유사하게,
죄악의 20 ∘ ⋅ 죄악의 40 ∘ ⋅ 죄악의 80 ∘ = 3 8 {\displaystyle \sin 20^{\circ }\cdot \sin 40^{\circ }\cdot \sin 80^{\circ }={\frac {\sqrt {3}}{8}} 는 x 20 {\displaystyle 20^{\circ}} . 죄악의 x ⋅ 죄악의 ( 60 ∘ − x ) ⋅ 죄악의 ( 60 ∘ + x ) = 죄악의 3 x 4 . {\displaystyle \sin x\cdot \sin \left(60^{\circ }-x\right)\cdot \sin \left(60^{\circ }+x\right)={\frac {\sin 3x}{4}}}
케이스 x 15 {\displaystyle 15^{\circ
죄악의 15 ∘ ⋅ 죄악의 45 ∘ ⋅ 죄악의 75 ∘ = 2 8 , 죄악의 15 ∘ ⋅ 죄악의 75 ∘ = 1 4 . {\displaystyle {\begin{aligned}\sin 15^{\circ }\cdot \sin 45^{\circ }\cdot \sin 75^{\circ }&={\frac {\sqrt {2}},\\sin 15^{\circ }\cdot \sin 75^{\circ }&={\frac {1}{4}}. \end{aligned}}
케이스 x 10 {\displaystyle 10^{\circ
죄악의 10 ∘ ⋅ 죄악의 50 ∘ ⋅ 죄악의 70 ∘ = 1 8 . {\displaystyle \sin 10^{\circ }\cdot \sin 50^{\circ }\cdot \sin 70^{\circ }={\frac {1}{8}}}
같은 코사인 아이덴티티는
cos x ⋅ cos ( 60 ∘ − x ) ⋅ cos ( 60 ∘ + x ) = cos 3 x 4 . {\displaystyle \cos x\cdot \cos \left(60^{\circ }-x\right)\cdot \cos \left(60^{\circ }+x\right)={\frac {\cos 3x}{4}}}
유사하게,
cos 10 ∘ ⋅ cos 50 ∘ ⋅ cos 70 ∘ = 3 8 , cos 15 ∘ ⋅ cos 45 ∘ ⋅ cos 75 ∘ = 2 8 , cos 15 ∘ ⋅ cos 75 ∘ = 1 4 . {\displaystyle {\begin{aligned}\cos 10^{\circ }\cdot \cos 50^{\circ }\cdot \cos 70^{\circ }&={\frac {\sqrt {3}}{8}}\cdot \cos 45^{\circ }\cdot \cos 75^{\circ }&={\frac {\sqrt {2}{8}},\cos 15^{\circ }\cdot \cos 75^{\circ }&={\frac {1}{4}}. \end{aligned}}
유사하게,
태닝한 50 ∘ ⋅ 태닝한 60 ∘ ⋅ 태닝한 70 ∘ = 태닝한 80 ∘ , 태닝한 40 ∘ ⋅ 태닝한 30 ∘ ⋅ 태닝한 20 ∘ = 태닝한 10 ∘ . {\displaystyle {\begin{aligned}\tan 50^{\circ }\cdot \tan 60^{\circ }&=\tan 80^{\circ },\tan 40^{\circ }\cdot \tan 30^{\circ }\cdot \tan 20^{\circ }&=\tan 10^{\circ }. \end{aligned}}
다음은 변수를 포함하는 항등식에 쉽게 일반화되지 않을 수 있습니다(단, 아래 설명 참조).
cos 24 ∘ + cos 48 ∘ + cos 96 ∘ + cos 168 ∘ = 1 2 . {\displaystyle \cos 24^{\circ }+\cos 48^{\circ }+\cos 96^{\circ }+\cos 168^{\circ }={\frac {1}{2}}}
21개의 분모로 동일성을 고려할 때, 도 측정은 라디안 측정보다 더 효율적이지 않게 됩니다.
cos 2 π 21 + cos ( 2 ⋅ 2 π 21 ) + cos ( 4 ⋅ 2 π 21 ) + cos ( 5 ⋅ 2 π 21 ) + cos ( 8 ⋅ 2 π 21 ) + cos ( 10 ⋅ 2 π 21 ) = 1 2 . {\displaystyle \cos {\frac {2\pi}{21}}+\cos \left(2\cdot {\frac {2\pi}{21}\right)+\cos \left(4\cdot {\frac {2\pi}{21}\right)+\cos \left(5\cdot {\frac {2\pi}{21}\right)+\cos \left(8\cdot {\frac {2\pi}{21}\right)+\cos \left(10\cdot {\frac {2\pi}{21}\right)={\frac {1}{2}}}
인자 1, 2, 4, 5, 8, 10은 패턴을 명확하게 만들기 시작할 수 있습니다. 이들 상대적으로 소수 이거나 공통적으로 소수 인자 가 없습니다. 마지막 몇 가지 예는 환원 불가능한 사이클로토믹 다항식 에 대한 기본적인 사실의 응집체입니다. 코사인은 해당 다항식의 0의 실제 부분입니다. 0의 합은 (위의 마지막 경우) 21에서 평가된 뫼비우스 함수입니다. 0의 절반만이 위에 있습니다. 이 마지막 ID 이전의 두 개의 ID는 동일한 방식으로 발생하며, 각각 21개가 10개와 15개로 대체되었습니다.
다른 코사인 아이덴티티는 다음과 같습니다.[48]
2 cos π 3 = 1 , 2 cos π 5 × 2 cos 2 π 5 = 1 , 2 cos π 7 × 2 cos 2 π 7 × 2 cos 3 π 7 = 1 , {\displaystyle {\begin{aligned}2\cos {\pi}{3}&=1,\2\cos {\frac {\pi}{5}}\time 2\cos {\frac {2\pi}{5}&=1,\2\cos {\frac {\pi}{7}\time 2\cos {\frac {2\pi}{7}\time 2\cos {\frac {3\pi}&=1,\end{aligned}} 모든 홀수에 대하여 등등. 그래서. cos π 3 + cos π 5 × cos 2 π 5 + cos π 7 × cos 2 π 7 × cos 3 π 7 + ⋯ = 1. {\displaystyle \cos {\frac {\pi }{3}}+\cos {\frac {\pi }{5}}\cos {\frac {2\pi }{5}}+\cos {\frac {\pi }{7}\cos {\frac {2\pi }{7}\times \cos {\frac {3\pi }{7}+ dots = 1}
이러한 호기심 많은 정체성은 다음과 같은 보다 일반적인 사실에서 비롯됩니다.[49]
∏ k = 1 n − 1 죄악의 k π n = n 2 n − 1 {\displaystyle \prod _{k=1}^{n-1}\sin {\frac {k\pi}{n}}={\frac {n}{2^{n-1}}}} 그리고. ∏ k = 1 n − 1 cos k π n = 죄악의 π n 2 2 n − 1 . {\displaystyle \prod _{k=1}^{n-1}\cos {\frac {k\pi}{n}}={\frac {\pin}{2}}}{2^{n-1}}}}
이것들을 합하면 우리는
∏ k = 1 n − 1 태닝한 k π n = n 죄악의 π n 2 {\displaystyle \prod _{k=1}^{n-1}\tan {\frac {k\pi}{n}}={\frac {n}{\sin {\frac {\pin}{2}}}}
n 이 홀수(n 2m 1 {\displaystyle 2m 1
∏ k = 1 m 태닝한 k π 2 m + 1 = 2 m + 1 {\displaystyle \prod _{k=1}^{m}\tan {\frac {k\pi}{2m+1}}={\sqrt {2m+1}}
버터워스 저역 통과 필터의 전달 함수 는 다항식과 극으로 표현할 수 있습니다.주파수를 차단 주파수로 설정하면 다음과 같은 동일성을 증명할 수 있습니다.
∏ k = 1 n 죄악의 ( 2 k − 1 ) π 4 n = ∏ k = 1 n cos ( 2 k − 1 ) π 4 n = 2 2 n {\displaystyle \prod _{k=1}^{n}\sin {\frac {\left(2k-1\right)\pi }{4n}}=\prod _{k=1}^{n}\cos {\frac {\left(2k-1\right)\pi }{4n}}={\frac {\sqrt {2}}{2^{n}}}}
컴퓨팅 computing π를 많은 숫자로 계산 하는 효율적인 방법은 Machine 으로 인해 변수가 없는 다음 ID를 기반으로 합니다. 이를 기계식 공식 이라고 합니다.
π 4 = 4 아크탄 1 5 − 아크탄 1 239 {\displaystyle {\frac {\pi}{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}} 또는 레온하르트 오일러 의 항등식을 사용하여 다음과 같이 나타낼 수 있습니다. π 4 = 5 아크탄 1 7 + 2 아크탄 3 79 {\displaystyle {\frac {\pi}{4}}=5\arctan {\frac {1}{7}}+2\arctan {\frac {3}{79}}} 또는 피타고라스 의 세 배 를 사용하여: π = 아코코 4 5 + 아코코 5 13 + 아코코 16 65 = 호신 3 5 + 호신 12 13 + 호신 63 65 . {\displaystyle \pi =\arccos {\frac {4}{5}}+\arccos {\frac {5}{13}}+\arccos {\frac {16}{65}}=\arcsin {\frac {3}{5}}+\arcsin {\frac {12}{13}}+\arcsin {\frac {63}{65}}.
그 밖에 다음이 있습니다.[50] [46]
π 4 = 아크탄 1 2 + 아크탄 1 3 , {\displaystyle {\frac {\pi}{4}}=\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}}} π = 아크탄 1 + 아크탄 2 + 아크탄 3 , {\displaystyle \pi =\arctan 1+\arctan 2+\arctan 3,} π 4 = 2 아크탄 1 3 + 아크탄 1 7 . {\displaystyle {\frac {\pi}{4}}=2\arctan {\frac {1}{3}}+\arctan {\frac {1}{7}}}
일반적으로 숫자 t , ...,t (- 1, 1) 에 대해 θ = σ 아크 ( π/4, 3 π/4), t tan( π/2 - θ) = 간이 침대 θ. 이 마지막 식은 접선이 t 1 , ...,t n −1(-1, 1)에 있는 각도의 합에 대한 공식을 사용하여 직접 계산할 수 있습니다. 특히 계산된 t n t 1 , ...,t n −1 이 값들을 가지고,
π 2 = ∑ k = 1 n 아크탄 ( t k ) π = ∑ k = 1 n sgn ( t k ) 아코코 ( 1 − t k 2 1 + t k 2 ) π = ∑ k = 1 n 호신 ( 2 t k 1 + t k 2 ) π = ∑ k = 1 n 아크탄 ( 2 t k 1 − t k 2 ) , {\displaystyle {\begin{aligned}{\frac {\pi}{2}}&=\sum _{k=1}^{n}\arctan(t_{k})\\\pi &=\sum _{k=1}^{n}\operatorname {sgn}(t_{k})\arccos \left ({\frac {1-t_{k}^{2}\right)\pi &=\sum _{k=1}^{n}\arcsin \left ({\frac {2t_{k}}{{k}}\right)\pi &=\sum _{k=1}^{n}\arctan \left ({\frac {2t_{k}}{1-t_{k}^{2}\right)\,\end{aligned}}\right}\right},\pi &=\sum _{k=1}^{n}\arctan \left )\frac {2t_{k}},\right)\right},\end{aligned}}
첫 번째 식을 제외한 모든 식에서 접선 반각 공식을 사용했습니다. 처음 k 하나 이상이 (-1, 1) 내에 있지 않을 경우에도 적용됩니다. 만약 p /q (2t, 1 - t , 1 + t )2pq ,q q p ).
예를 들어, n 3항 의 경우,
π 2 = 아크탄 ( a b ) + 아크탄 ( c d ) + 아크탄 ( b d − a c a d + b c ) {\displaystyle {\frac {\pi}{2}}=\arctan \left ({\frac {a}{b}}\right)+\arctan \left ({\frac {c}{d}\right)+\arctan \left ({\frac {ad+bc}\right)} a ,b ,c ,d 0 인 경우.
유클리드의 정체 유클리드 는 원에 새겨진 정육각형의 변에 있는 정사각형의 넓이가 정육각형의 변에 있는 정사각형의 넓이의 합과 같은 원에 새겨진 정육각형의 변에 있는 정사각형의 넓이의 합과 같다는 것을 그의 원소 현대 삼각법의 언어로 다음과 같이 말합니다.
죄악의 2 18 ∘ + 죄악의 2 30 ∘ = 죄악의 2 36 ∘ . {\displaystyle \sin ^{2}18^{\circ }+\sin ^{2}30^{\circ }=\sin ^{2}36^{\circ }}
프톨레마이오스 는 알마게스트 그의 화음표 에서 일부 각도를 계산하기 위해 이 명제를 사용했습니다.
삼각함수의 구성 이러한 항등식은 삼각함수의 삼각함수를 포함합니다.[51]
cos ( t 죄악의 x ) = J 0 ( t ) + 2 ∑ k = 1 ∞ J 2 k ( t ) cos ( 2 k x ) {\displaystyle \cos(t\sin x)= J_{0}(t)+2\sum _{k=1}^{\infty}J_{2k}(t)\cos(2kx)} 죄악의 ( t 죄악의 x ) = 2 ∑ k = 0 ∞ J 2 k + 1 ( t ) 죄악의 ( ( 2 k + 1 ) x ) {\displaystyle \sin(t\sin x)=2\sum _{k=0}^{\infty}J_{2k+1}(t)\sin {\big (}(2k+1)x{\big )}} cos ( t cos x ) = J 0 ( t ) + 2 ∑ k = 1 ∞ ( − 1 ) k J 2 k ( t ) cos ( 2 k x ) {\displaystyle \cos(t\cos x)= J_{0}(t)+2\sum _{k=1}^{\infty}(-1)^{k}J_{2k}(t)\cos(2kx)} 죄악의 ( t cos x ) = 2 ∑ k = 0 ∞ ( − 1 ) k J 2 k + 1 ( t ) cos ( ( 2 k + 1 ) x ) {\displaystyle \sin(t\cos x)=2\sum _{k=0}^{\infty}(-1)^{k}J_{2k+1}(t)\cos {\big (}(2k+1)x{\big )}} 여기서 J 는i Bessel 함수 입니다.
α + β + γ = 180°인 경우에 대한 추가 "조건부" 식별다음 공식은 임의의 평면 삼각형에 적용되며 공식에서 발생하는 함수가 잘 정의되어 있는 한 β + 180 , displaystyle \alpha +\ +\ 180^{\circ
태닝한 α + 태닝한 β + 태닝한 γ = 태닝한 α 태닝한 β 태닝한 γ 1 = 간이 침대 β 간이 침대 γ + 간이 침대 γ 간이 침대 α + 간이 침대 α 간이 침대 β 간이 침대 ( α 2 ) + 간이 침대 ( β 2 ) + 간이 침대 ( γ 2 ) = 간이 침대 ( α 2 ) 간이 침대 ( β 2 ) 간이 침대 ( γ 2 ) 1 = 태닝한 ( β 2 ) 태닝한 ( γ 2 ) + 태닝한 ( γ 2 ) 태닝한 ( α 2 ) + 태닝한 ( α 2 ) 태닝한 ( β 2 ) 죄악의 α + 죄악의 β + 죄악의 γ = 4 cos ( α 2 ) cos ( β 2 ) cos ( γ 2 ) − 죄악의 α + 죄악의 β + 죄악의 γ = 4 cos ( α 2 ) 죄악의 ( β 2 ) 죄악의 ( γ 2 ) cos α + cos β + cos γ = 4 죄악의 ( α 2 ) 죄악의 ( β 2 ) 죄악의 ( γ 2 ) + 1 − cos α + cos β + cos γ = 4 죄악의 ( α 2 ) cos ( β 2 ) cos ( γ 2 ) − 1 죄악의 ( 2 α ) + 죄악의 ( 2 β ) + 죄악의 ( 2 γ ) = 4 죄악의 α 죄악의 β 죄악의 γ − 죄악의 ( 2 α ) + 죄악의 ( 2 β ) + 죄악의 ( 2 γ ) = 4 죄악의 α cos β cos γ cos ( 2 α ) + cos ( 2 β ) + cos ( 2 γ ) = − 4 cos α cos β cos γ − 1 − cos ( 2 α ) + cos ( 2 β ) + cos ( 2 γ ) = − 4 cos α 죄악의 β 죄악의 γ + 1 죄악의 2 α + 죄악의 2 β + 죄악의 2 γ = 2 cos α cos β cos γ + 2 − 죄악의 2 α + 죄악의 2 β + 죄악의 2 γ = 2 cos α 죄악의 β 죄악의 γ cos 2 α + cos 2 β + cos 2 γ = − 2 cos α cos β cos γ + 1 − cos 2 α + cos 2 β + cos 2 γ = − 2 cos α 죄악의 β 죄악의 γ + 1 죄악의 2 ( 2 α ) + 죄악의 2 ( 2 β ) + 죄악의 2 ( 2 γ ) = − 2 cos ( 2 α ) cos ( 2 β ) cos ( 2 γ ) + 2 cos 2 ( 2 α ) + cos 2 ( 2 β ) + cos 2 ( 2 γ ) = 2 cos ( 2 α ) cos ( 2 β ) cos ( 2 γ ) + 1 1 = 죄악의 2 ( α 2 ) + 죄악의 2 ( β 2 ) + 죄악의 2 ( γ 2 ) + 2 죄악의 ( α 2 ) 죄악의 ( β 2 ) 죄악의 ( γ 2 ) {\displaystyle {\begin {aligned}\tan \alpha +\tan \gamma +\tan \beta &=\tan \alpha \tan \tan \gamma \cot \gamma \cot \cot \gamma +\cot \cot \alpha +\cot \cot \beta \\cot \({ \\left ({\frac {2}}\right)+\cot \left beta \frac {\({}{2}\right)+\cot \left gamma \frac {\({}{2}\right)&=\cot \left beta\frac {\alpha }{2}\right)\cot \left \left \left \left \left \left \lepha \lepha \left \lepha \lepha \lepha \left \lepha \lepha \lepha \left \lepha \lepha \lepha \lepha \lepha \lepha \lepha \lepha \lepha \lepha \ {\frac {\beta }{2}\right)\cot \left ({\frac {\gamma }{2}\right)\1&=\tan \left ({\frac {\beta }{2}\right)\tan \left ({\frac {\gamma }{2}\right)+\tan \left ({\frac {\alpha}{2}\right)\tan \left ({\frac {\alpha}{2}\right)+\tan \left ({\frac {\alpha}{2}\right)\tan \left ({\frac {\beta }{2}\right)\tan \left gamma \frac {\right)\right) \\\sin \alpha +\sin \beta +\sin \gamma &=4\cos \left ({\frac {\alpha}{2}}\right)\cos \left ({\frac {\beta }{2}\right)\cos \left ({\frac {\gamma }{2}\right)\cos \left ({+\sin \left beta\frac {\alpha }{2}\right)\sin \left ({\frac {\gamma }{2}\right)\sin \left ({\frac {\beta }{2}\right)\right)\sin \left gamma\frac {\}}}{2}\right)\right) \\cos \alpha +\cos \beta +\cos \gamma &=4\sin \left ({\frac {\alpha}{2}}\right)\sin \left ({\frac {\beta }{2}\right)\sin \left ({\frac {\gamma }{2}\right)+1\\cos \alpha +\cos \left ({\frac {\alpha }{2}\right)\cos \left ({\frac {\beta }{2}\right)\cos \left ({\frac {\gamma }{2}\right)\cos \left beta\frac {\gamma}{2}\right)-1\sin (2\alpha )+\sin (2\beta )+\sin (2)+\sin (2) (2\gamma)&=4\sin \alpha \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \s \sin \sin \sin \sin \sin \sin \s \sin \s 감마 &=2\cos \alpha \cos \cos \gamma \cos \beta +2\-\sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma &=2\cos \sin \beta \sin \sin \gamma \\\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma &=-2\cos \alpha \cos \cos \beta +1\-\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\beta &=-2\cos \sin \sin \gamma +1\\\sin ^{2}(2\alpha )+\sin ^{sin ^{2}\sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin +1\alpha \sin \sin \sin \sin \sin \sin \sin \sin \sin \sin gamma 2}(2\beta )+\sin ^{2}(2\gamma )&=-2\cos(2\alpha )\cos(2\beta )\cos(2\gamma )+2\cos ^{2}(2\beta )+\cos ^{2}(2\gamma )+\cos ^{2}(2\beta )&=2\cos ^{2}(2\alpha )\,\cos(2\({ )\,\cos(2\gamma )\,\cos(2\alpha )+1&=\sin ^{2}\right)+\sin ^{2}\left ({\frac {\beta }{2}\right)+\sin ^{2}\left ({\frac {\gamma }{2}\right)+\sin ^{2}\left ({\frac {\ {}{2}\right)+2\sin \left ({\frac {\alpha}{{ 2},\right)\,\sin \left ({\frac {\beta }{2}\right)\,\sin \left ({\frac {\gamma }{2}\right)\end{aligned}}
역사속기 항해에는 버진 (versine ), 커버진(coversine), 하버진(haversine ), 엑센트(execent )가 사용되었습니다. 예를 들어, haversine 공식 은 구 위의 두 점 사이의 거리를 계산하는 데 사용되었습니다. 오늘날에는 거의 사용되지 않습니다.
여러가지 종류의 모든 삼각형 비율 간의 관계 다음 항등식은 각각 모든 삼각형 비율 사이의 관계를 나타냅니다.
( 죄악의 θ + csc θ ) 2 + ( cos θ + 초 θ ) 2 − ( 태닝한 θ + 간이 침대 θ ) 2 = 5 {\displaystyle (\sin \theta +\csc \theta )^{2}+(\cos \theta +\sec \theta )^{2}-(\tan \theta +\cot \theta )^{2}=5} ( 죄악의 θ + csc θ ) 2 + ( cos θ + 초 θ ) 2 − ( 태닝한 θ − 간이 침대 θ ) 2 = 9 {\displaystyle (\sin \theta +\csc \theta )^{2}+(\cos \theta +\sec \theta )^{2}-(\tan \theta -\cot \theta )^{2}=9}
유사하게,
( 죄악의 θ + csc θ ) 2 + ( cos θ + 초 θ ) 2 = 태닝한 2 θ + 간이 침대 2 θ + 7 {\displaystyle (\sin \theta +\csc \theta )^{2}+(\cos \theta +\sec \theta )^{2}=\tan ^{2}\theta +\cot ^{2}\theta +7}
디리클레 커널 디리클레 커널 Dn (x )
1 + 2 cos x + 2 cos ( 2 x ) + 2 cos ( 3 x ) + ⋯ + 2 cos ( n x ) = 죄악의 ( ( n + 1 2 ) x ) 죄악의 ( 1 2 x ) . {\displaystyle 1+2\cos x+2\cos(2x)+2\cos(3x)+2\cdots +2\cos(nx)={\frac {\sin \left(n+{\frac {1}{2}}\right)x\right) }{\sin \left ({\frac {1}{2}}x\right}}}}.
기간 2 {\displaystyle 2\pi} 적분 가능 한 함수와 디리클레 커널의 컨볼루션 은 함수의 n {\displaystyle n} 측정 또는 일반화 함수 에 대해서도 동일한 값이 적용됩니다.
접선반각치환 설정하면
t = 태닝한 x 2 , {\displaystyle t=\tan {\frac {x}{2}},} 그[52] 죄악의 x = 2 t 1 + t 2 ; cos x = 1 − t 2 1 + t 2 ; e i x = 1 + i t 1 − i t {\displaystyle \sin x={\frac {2t}{1+t^{2}};\qquad \cos x={\frac {1-t^{2}}{1+t^{2}};\qquad e^{ix}={\frac {1+it}{1-it}} 여기서 e x cos x x 있고 {\displaystyle e^{ix cos x+i\sin x,} 때때로 cis x
t {\displaystyle t} tan x / 2 sin {\displaystyle \sin } 2t / 1 t cos x {\displaystyle \cos x} t / 1 t dx 가 2dt / 1 t 따라서 sin x {\displaystyle \sin x} cos x {\displaystyle \cos x} 함수 displaystyle } 유도체 를 찾습니다.
비엣의 무한한 제품
cos θ 2 ⋅ cos θ 4 ⋅ cos θ 8 ⋯ = ∏ n = 1 ∞ cos θ 2 n = 죄악의 θ θ = sinc θ . {\displaystyle \cos {\frac {\theta}{2}}\cdot \cos {\frac {\theta}{4}}\cdot \cos {\frac {\theta}{8}}\cdots =\prod _{n=1}^{\infty }\cos {\frac {\theta}{2^{n}}={\frac {\sin \theta}{\theta}}}=\operatorname {sinc} \theta}
참고 항목 참고문헌 ^ Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [June 1964]. "Chapter 4, eqn 4.3.45" . Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables ISBN 978-0-486-61272-0 LCCN 64-60036 . MR 0167642 . LCCN 65-12253 .^ 셀비 1970 , 페이지 188^ 아브라모위츠와 스테건, 페이지 72, 4.3.13–15 ^ 아브라모위츠와 스테건, 페이지 72, 4.3.7–9 ^ 아브라모위츠와 스테건, 페이지 72, 4.3.16 ^ a b c d Weisstein, Eric W. "Trigonometric Addition Formulas" . MathWorld ^ 아브라모위츠와 스테건, 페이지 72, 4.3.17 ^ 아브라모위츠와 스테건, 페이지 72, 4.3.18 ^ a b "Angle Sum and Difference Identities" . www.milefoot.com . Retrieved 2019-10-12 .^ 아브라모위츠와 스테건, 페이지 72, 4.3.19 ^ 아브라모위츠와 스테건, 페이지 80, 4.4.32 ^ 아브라모위츠와 스테건, 페이지 80, 4.4.33 ^ 아브라모위츠와 스테건, 페이지 80, 4.4.34 ^ Bronstein, Manuel (1989). "Simplification of real elementary functions". In Gonnet, G. H. (ed.). Proceedings of the ACM-SIGSAM 1989 International Symposium on Symbolic and Algebraic Computation . ISSAC '89 (Portland US-OR, 1989-07). New York: ACM . pp. 207–211. doi :10.1145/74540.74566 . ISBN 0-89791-325-6 ^ Michael Hardy (August–September 2016). "On Tangents and Secants of Infinite Sums" . American Mathematical Monthly . 123 (7): 701–703. doi :10.4169/amer.math.monthly.123.7.701 . S2CID 126310545 . ^ "Sine, Cosine, and Ptolemy's Theorem" .^ "Sine, Cosine, and Ptolemy's Theorem" .^ a b Weisstein, Eric W. "Multiple-Angle Formulas" . MathWorld ^ 아브라모위츠와 스테건, 페이지 74, 4.3.48 ^ a b 셀비 1970 , 페이지 190^ Weisstein, Eric W. "Multiple-Angle Formulas" . mathworld.wolfram.com . Retrieved 2022-02-06 . ^ Ward, Ken. "Multiple angles recursive formula" . Ken Ward's Mathematics Pages . ^ a b Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [June 1964]. "Chapter 4, eqn 4.3.20-22" . Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables ISBN 978-0-486-61272-0 LCCN 64-60036 . MR 0167642 . LCCN 65-12253 .^ a b Weisstein, Eric W. "Half-Angle Formulas" . MathWorld ^ 아브라모위츠와 스테건, 페이지 72, 4.3.24-26 ^ Weisstein, Eric W. "Double-Angle Formulas" . MathWorld ^ 아브라모위츠와 스테건, 페이지 72, 4.3.27–28 ^ 아브라모위츠와 스테건, 페이지 72, 4.3.31-33 ^ Eves, Howard (1990). An introduction to the history of mathematics (6th ed.). Philadelphia: Saunders College Pub. p. 309. ISBN 0-03-029558-0 OCLC 20842510 . ^ 아브라모위츠와 스테건, 페이지 72, 4.3.34–39 ^ Johnson, Warren P. (Apr 2010). "Trigonometric Identities à la Hermite". American Mathematical Monthly 117 (4): 311–327. doi :10.4169/000298910x480784 . S2CID 29690311 . ^ "Product Identity Multiple Angle" .^ Apostol, T.M. (1967) 미적분학 2판. 뉴욕, 뉴욕, 와일리. 334-335쪽. ^ a b Weisstein, Eric W. "Harmonic Addition Theorem" . MathWorld ^ Ortiz Muñiz, Eddie (Feb 1953). "A Method for Deriving Various Formulas in Electrostatics and Electromagnetism Using Lagrange's Trigonometric Identities". American Journal of Physics . 21 (2): 140. Bibcode :1953AmJPh..21..140M . doi :10.1119/1.1933371 . ^ Agarwal, Ravi P.; O'Regan, Donal (2008). Ordinary and Partial Differential Equations: With Special Functions, Fourier Series, and Boundary Value Problems ISBN 978-0-387-79146-3 185페이지 발췌 ^ Jeffrey, Alan; Dai, Hui-hui (2008). "Section 2.4.1.6". Handbook of Mathematical Formulas and Integrals (4th ed.). Academic Press. ISBN 978-0-12-374288-9 ^ Fay, Temple H.; Kloppers, P. Hendrik (2001). "The Gibbs' phenomenon" . International Journal of Mathematical Education in Science and Technology . 32 (1): 73–89. doi :10.1080/00207390117151 . ^ 아브라모위츠와 스테건, 페이지 74, 4.3.47 ^ 아브라모위츠와 스테건, 페이지 71, 4.3.2 ^ 아브라모위츠와 스테건, 페이지 71, 4.3.1 ^ 아브라모위츠와 스테건, 페이지 80, 4.4.26–31 ^ 아브라모위츠와 스테건, p. 75, 4.3.89–90 ^ 아브라모위츠와 스테건, 페이지 85, 4.5.68–69 ^ 아브라모위츠 & 스테건 1972 , 페이지 73, 4.3.45^ a b c 우, 렉스 H. "말 없는 증명: 오일러의 아크탄젠트 정체성", 수학잡지 77(3), 2004년 6월, 189페이지 ^ S. M. Abrarov, R. K. Jagpal, R. Siddiqui and B. M. Quine (2021), "Algorithmic determination of a large integer in the two-term Machin-like formula for π", Mathematics , 9 (17), 2162, doi :10.3390/math9172162 {{citation }}: CS1 유지 : 여러 이름 : 저자 목록 (링크 ) ^ Humble, Steve (Nov 2004). "Grandma's identity". Mathematical Gazette . 88 : 524–525. doi :10.1017/s0025557200176223 . S2CID 125105552 . ^ Weisstein, Eric W. "Sine" . MathWorld ^ 해리스, 에드워드 M. "Arctangents의 합", 로저 B. Nelson, 단어 없는 증명들 (1993, 미국수학협회), p. 39. ^ Milton Abramowitz and Irene Stegun, 공식, 그래프 수학 표 포함한 수학 함수 핸드북 도버 출판사 , 뉴욕, 1972, 공식 9.1.42–9.1.45^ 아브라모위츠와 스테건, 페이지 72, 4.3.23
서지학 Abramowitz, Milton ; Stegun, Irene A. , eds. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables Dover Publications . ISBN 978-0-486-61272-0 Nielsen, Kaj L. (1966), Logarithmic and Trigonometric Tables to Five Places (2nd ed.), New York: Barnes & Noble , LCCN 61-9103 Selby, Samuel M., ed. (1970), Standard Mathematical Tables (18th ed.), The Chemical Rubber Co. 외부 링크 






















































 통해 주어진 선과 평행하게 각도가 결정되는 유클리드 공간의 선에도 동일한 개념이 적용될 수 있습니다.
통해 주어진 선과 평행하게 각도가 결정되는 유클리드 공간의 선에도 동일한 개념이 적용될 수 있습니다.


















































![{\displaystyle {\begin{aligned}\operatorname {sgn}(\sin \theta )=\operatorname {sgn}(\csc \theta )&={\begin{cases}+1&{\text{if}}\ \ 0<\theta <\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <0\\0&{\text{if}}\ \ \theta \in \{0,\pi \}\end{cases}}\\[5mu]\operatorname {sgn}(\cos \theta )=\operatorname {sgn}(\sec \theta )&={\begin{cases}+1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },{\tfrac {1}{2}}\pi {\bigr \}}\end{cases}}\\[5mu]\operatorname {sgn}(\tan \theta )=\operatorname {sgn}(\cot \theta )&={\begin{cases}+1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ 0<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <0\ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },0,{\tfrac {1}{2}}\pi ,\pi {\bigr \}}\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14cc79239a0fcdfb53b132d75a93474e9e6d5ba0)
























![{\displaystyle {\begin{aligned}e_{0}&=1\\[6pt]e_{1}&=\sum _{i}x_{i}&&=\sum _{i}\tan \theta _{i}\\[6pt]e_{2}&=\sum _{i<j}x_{i}x_{j}&&=\sum _{i<j}\tan \theta _{i}\tan \theta _{j}\\[6pt]e_{3}&=\sum _{i<j<k}x_{i}x_{j}x_{k}&&=\sum _{i<j<k}\tan \theta _{i}\tan \theta _{j}\tan \theta _{k}\\&{}\ \ \vdots &&{}\ \ \vdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fe5c7c43e0176206f134067e005328cb0a31cce)

![{\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2})&={\frac {e_{1}}{e_{0}-e_{2}}}={\frac {x_{1}+x_{2}}{1\ -\ x_{1}x_{2}}}={\frac {\tan \theta _{1}+\tan \theta _{2}}{1\ -\ \tan \theta _{1}\tan \theta _{2}}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\[8pt]&={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c9196b8ab5e0aef6cf7d7fec7d7546f2a6e7d2f)
![{\displaystyle {\begin{aligned}\sec \left(\sum _{i}\theta _{i}\right)&={\frac {\prod _{i}\sec \theta _{i}}{e_{0}-e_{2}+e_{4}-\cdots }}\\[8pt]\csc \left(\sum _{i}\theta _{i}\right)&={\frac {\prod _{i}\sec \theta _{i}}{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7d12744003bcf5becf301096c3d12ca1d1e1055)

![{\displaystyle {\begin{aligned}\sec(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{1-\tan \alpha \tan \beta -\tan \alpha \tan \gamma -\tan \beta \tan \gamma }}\\[8pt]\csc(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{\tan \alpha +\tan \beta +\tan \gamma -\tan \alpha \tan \beta \tan \gamma }}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e082e69aab7a9c782f590f3a93262ba3101899b7)




























![{\displaystyle {\begin{aligned}\sin {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {1-\cos \theta }{2}}}\\[3pt]\cos {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {1+\cos \theta }{2}}}\\[3pt]\tan {\frac {\theta }{2}}&={\frac {1-\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1+\cos \theta }}=\csc \theta -\cot \theta ={\frac {\tan \theta }{1+\sec {\theta }}}\\[6mu]&=\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}={\frac {-1+\operatorname {sgn}(\cos \theta ){\sqrt {1+\tan ^{2}\theta }}}{\tan \theta }}\\[3pt]\cot {\frac {\theta }{2}}&={\frac {1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }}=\csc \theta +\cot \theta =\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\\sec {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1+\cos \theta }}}\\\csc {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1-\cos \theta }}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d53d104c73c4b28f1dd7bfa5d2b0c7207c68cd87)
![{\displaystyle {\begin{aligned}\tan {\frac {\eta \pm \theta }{2}}&={\frac {\sin \eta \pm \sin \theta }{\cos \eta +\cos \theta }}\\[3pt]\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\[3pt]{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta }{2}}\right|}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/639270245e163f1afa8682ac8aa12086db43dce1)








![{\displaystyle {\begin{aligned}\tan {\frac {\theta }{2}}&=\csc \theta -\cot \theta \\&=\pm \,{\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}\\[3pt]&={\frac {\sin \theta }{1+\cos \theta }}\\[3pt]&={\frac {1-\cos \theta }{\sin \theta }}\\[5pt]\tan {\frac {\eta +\theta }{2}}&={\frac {\sin \eta +\sin \theta }{\cos \eta +\cos \theta }}\\[5pt]\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\[5pt]{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta }{2}}\right|}}\\[5pt]\tan {\frac {\theta }{2}}&={\frac {\tan \theta }{1+{\sqrt {1+\tan ^{2}\theta }}}}\\&{\text{for }}\theta \in \left(-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cab50a58d64b8c3341fb4f7646888bbbc67ea0c)
![{\displaystyle {\begin{aligned}\cot {\frac {\theta }{2}}&=\csc \theta +\cot \theta \\&=\pm \,{\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\[3pt]&={\frac {\sin \theta }{1-\cos \theta }}\\[4pt]&={\frac {1+\cos \theta }{\sin \theta }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c9be831a310f112ffc6e5790bc705dc7b070b87)

























![{\displaystyle {\begin{aligned}\prod _{k=1}^{n}\cos \theta _{k}&={\frac {1}{2^{n}}}\sum _{e\in S}\cos(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\\[6pt]&{\text{where }}e=(e_{1},\cdots ,e_{n})\in S=\{1,-1\}^{n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fd64569e849d81a789af29a156b51346985b121)






 (는) 빈
(는) 빈














![{\displaystyle {\begin{aligned}\sum _{k=0}^{n}\sin k\theta &={\frac {\cos {\tfrac {1}{2}}\theta -\cos \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\\[5pt]\sum _{k=0}^{n}\cos k\theta &={\frac {\sin {\tfrac {1}{2}}\theta +\sin \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c850aa2dd7cc306d87d5d68d5802cab64f8572a0)





 분수 변환
분수 변환



 위에서
위에서 


























![{\displaystyle {\begin{alignedat}{9}{\frac {\pi }{2}}~&=~\arcsin(x)&&+\arccos(x)~&&=~\arctan(r)&&+\operatorname {arccot}(r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arccsc}(s)\\[0.4ex]\pi ~&=~\arccos(x)&&+\arccos(-x)~&&=~\operatorname {arccot}(r)&&+\operatorname {arccot}(-r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arcsec}(-s)\\[0.4ex]0~&=~\arcsin(x)&&+\arcsin(-x)~&&=~\arctan(r)&&+\arctan(-r)~&&=~\operatorname {arccsc}(s)&&+\operatorname {arccsc}(-s)\\[1.0ex]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/839db041f421b4af5890106450e2b4d3e9e183d4)














































