DFT 행렬

응용수학에서 DFT 매트릭스는 이산 푸리에 변환(DFT)을 변환 매트릭스로 표현한 것으로, 매트릭스 곱셈을 통해 신호에 적용할 수 있다.

정의

N-점 DFT는 $곱셈{\displaystyle }$X = ${\displaystyle W}$ x$${\$displaystyle$ X$}$로 표시되며$,$ $여기$서 x$${\$displaystyle X}$은(는) 원래 입력 신호$,$ W {\$displaystyle$ W$}$은(는) N-by N 제곱 DFT 매트릭스, X ${\displaystystyty X}$은 신호의 $DFT$이다.

변환 매트릭스 $W{\displaystyle }$ ${\displaystyle W}$은(는) $W{\displaystyle }$=${\displaystyle {}_{}}$(${\displaystyle {\Omega \frac{{}^{}}{}}_{}}$ ${\displaystyle {\frac{{}^{}}{\sqrt{}}}_{}}$ N${\displaystyle {\frac{}{}}_{}}$) ${\displaystyle {,}_{}}$ ${\displaystyle k_{}}$= ${\displaystyle {0,\dots ,}_{}}$ N${\displaystyle {}_{}}$- ${\displaystyle 1_{}}$ ${\$또는 동등하게 정의할 수 있다$$.

${\displa$Ystyle W={\frac{1}{\sqrt{N}}}{\begin{bmatrix}1&, 1&, 1&, 1&, \cdots &, 1\\1&,\omega&\omega ^{2}&,\omega ^{3}&, \cdots &,\omega ^{N-1}\\1&,\omega ^{2}&,\omega ^{4}&,\omega ^{6}&, \cdots &,\omega ^{2(N-1)}\\1&,\omega ^{3}&,\omega ^{6}&,\omega ^{9}&, \cdots &,\omega ^{3(N-1)}\\\vdots&\vdots. &\vdots, \vdots &, \ddots &, \vdots \\1& &,\omega ^{N-1}&,\omega ^{2(N-1)}&,\omega ^{3(N-1)}&amp을 말한다.$\cdots &\omega ^{{(N-1)}\end{bmatrix$

where ${\displaystyle \omega =e^{-2\pi i/N}}$ is a primitive Nth root of unity in which ${\displaystyle i^{2}=-1}$. We can avoid writing large exponents for ${\displaystyle \omega }$ using the fact that for any exponent ${\displaystyle x}$ we have the identity ${\displaystyle {\omega }^x={\omega }^{x\mathrm{mo}}}$${\displaystyle d^{}}$ ${\displaystyle N^{}}$. ${\displaystyle \omega ^{x}=\omega ^{x\mod N}}$ 이것은$$ 정상화 요인까지 단결의 뿌리에 대한 반데르몬드 행렬이다. 합계 $앞$의 정규화 계수(1${\displaystyle }$/ ${\displaystyle N\sqrt{}}$ ${\$와 Ω으로 된 지수 부호는 단순한 규약일 뿐이며, 일부 치료법에서는 차이가 있다는 점에 유의하십시오. 다음의 모든 논의는 관례에 관계없이 적용되며, 기껏해야 사소한 조정으로 이루어진다. 다만 중요한 것은 전진 및 역변환에 반대되는 부호지수가 있고, 그 정규화 인자의 산물이 1/N이라는 점이다. 그러나 $여기$서의 1${\displaystyle }$/ ${\displaystyle N\sqrt{}}$ ${\$을 선택하면$$ 결과 DFT 매트릭스가 단일화되어 여러 가지 상황에서 편리하다.

패스트 푸리에 변환 알고리즘은 매트릭스의 대칭을 활용하여 통상적인 $O{\displaystyle }$( ${\displaystyle {N\mathrm{}}^{}}$ ${\displaystyle {}^{}}$) ${\displaystyle O(N^{2})$에서 이 매트릭스에 벡터를 곱하는 시간을 줄인다$.$ 이와 유사한 기법을 Hadamard 매트릭스 및 월시 매트릭스와 같은 매트릭스에 의한 곱셈에 적용할 수 있다.

예

투 포인트

2점 DFT는 간단한 경우로, 첫 번째 항목은 DC(sum)이고 두 번째 항목은 AC(차이)이다.

${\displaystyle W={\frac {1}{\sqrt{2}}:{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}}}}$

첫 번째 행은 합을 수행하고, 두 번째 행은 차이를 수행한다.

1/${\displaystyle 2\sqrt{\mathrm{}}}$ ${\$}}의$$인수는 변환을 단일화하는 것이다${\displaystyle (}$아래 참조).

사점

시계방향 DFT 매트릭스는 다음과 같다.

${\displaystyle W={\frac{1}{\sqrt{4}}}{\begin{bmatrix}\omega ^{0}&,\omega ^{0}&,\omega ^{0}&,\omega ^{0}\\\omega ^{0}&,\omega ^{1}&,\omega ^{2}&,\omega ^{3}\\\omega ^{0}&,\omega ^{2}&,\omega ^{4}&,\omega ^{6}\\\omega ^{0}&,\omega ^{3}&,\omega ^{6}&, \omega ^{9}\\\end{bmatrix}}={\frac{1}{\sqrt{4}}}{\begin{bmatri.x}1&, 1&, 1&, 1\\1&, -i&, -1&, i\\1&, -1&, 1&, -1\\1&, i&, -1&, -i\end{b매트릭스}}$

여기서 $\Omega {\displaystyle }$= e${\displaystyle {}^{}}$- ${\displaystyle {2\frac{\mathrm{}}{}}^{}}$ ${\displaystyle {\frac{\pi }{}}^{}}$ i ${\displaystyle {\frac{\mathrm{}}{}}^{}}$=${\displaystyle }$- ${\displaystyle i}$ ${\displaystyle \omega =e^{-{\frac {2\pi i}{4}}}=-i}$.

팔점

두 경우의 첫 번째 비경쟁 정수 검정력은 다음과 같은 8점이다.

${\displaystyle W={\frac{1}{\sqrt{8}}}{\begin{bmatrix}\omega ^{0}&,\omega ^{0}&,\omega ^{0}&,\omega ^{0}&,\omega ^{0}&,\omega ^{0}&,\omega ^{0}&,\omega ^{0}\\\omega ^{0}&,\omega ^{1}&,\omega ^{2}&,\omega ^{3}&,\omega ^{4}&,\omega ^{5}&,\omega ^{6}&,\omega ^{7}\\\omega ^{0}&,\omega ^{2}&,\omega ^{4}&a.Mp,\omega ^{6}&,\omega ^{8}&,\omega ^{10}&,\omega ^{12}&,\omega ^{14}\\\.오메가 ^{0}&,\omega ^{3}&,\omega ^{6}&,\omega ^{9}&,\omega ^{12}&,\omega ^{15}&,\omega ^{18}&,\omega ^{21}\\\omega ^{0}&,\omega ^{4}&,\omega ^{8}&,\omega ^{12}&,\omega ^{16}&,\omega ^{20}&,\omega ^{24}&,\omega ^{28}\\\omega ^{0}&,\omega ^{5}&,\omega ^{10}&,\omega ^{15}&,\omega ^{20}&,\omega ^{.25}&\omega ^{30}&,\omega ^{35}\\\omega ^{0}&,\omega ^{6}&,\omega ^{12}&,\omega ^.{18}&,\omega ^{24}&,\omega ^{30}&,\omega ^{36}&,\omega ^{42}\\\omega ^{0}&,\omega ^{7}&,\omega ^{14}&,\omega ^{21}&,\omega ^{28}&,\omega ^{35}&,\omega ^{42}&, \omega ^{49}\\\end{bmatrix}}={\frac{1}{\sqrt{8}}}{\begin{bmatrix}1&, 1&, 1&, 1&, 1&, 1&, 1&, 1\\1&,\omega&-i&,-i\omega&-1&-.\omega&i&,i\omega \\1&, -i&, -1&, i&, 1&, -i&, -1&, i\\1&,-i\omega&i&,\omega&-1&,i\omega&-i&,-\omega \\1&, -1.&1&1&1&1&1&1\\1&#1&#1&#1&#1&#1&#1&#1&#1&i&#1&i&i&#1&#1&i&#1&i-i&i-i&#1&#1&i&i&i&i&#1\endomega\{bmatrix}$

어디에

${\displaystyle \omega =e^{-{\frac {2\pi i}{8}}={\frac {1}{\sqrt{2}}-{\frac {i}{\sqrt{2}}:}$

(참고: $\Omega {\displaystyle {}^{}}$ ${\displaystyle {8\mathrm{}}^{}}$+ ${\displaystyle n^{}}$= ${\displaystyle {\Omega }^{}}$ n ${\$

다음 이미지는 DFT를 행렬 곱셈으로 묘사하며, 행렬의 요소는 복잡한 지수 표본으로 묘사된다.

실제 부분(코사인파)은 고체 선으로, 가상 부분(사인파)은 점선으로 나타낸다.

상단 행은 모두 하나이므로(단위성을 위해$$ 1/${\$ 1$/{\sqrt{8})$ 입력 신호에서 DC 성분을 "측정"한다. 다음 행은 복잡한 지수에서 음의 한 사이클의 샘플 8개, 즉 부분 주파수가 -1/8인 신호로, 신호에서 부분 주파수 +1/8에서 "강도"가 얼마나 있는지 "측정"한다. 일치하는 필터는 우리가 찾고 있는 모든 것의 시간 역방향 버전과 신호를 비교하므로, 1/8을 찾을 때 fracfreq. -1/8과 비교하므로 이 행이 음의 주파수인 것이다. 다음 행은 복잡한 지수에서 음의 두 사이클로 8군데에서 샘플링되므로 -1/4의 부분 주파수를 가지며, 따라서 신호의 부분 주파수가 +1/4인 범위를 "측정"한다.

다음은 8포인트 DFT의 작동 방식을 부분 주파수로 요약한 것이다.

• 0은 신호에 있는 DC의 양을 측정한다.
• -1/8은 신호의 부분 주파수가 +1/8인 정도를 측정한다.
• -1/4 신호의 부분 주파수가 +1/4인 정도를 측정한다.
• -3/8 신호의 부분 주파수가 +3/8인 정도를 측정한다.
• -1/2 신호의 부분 주파수가 +1/2인 정도를 측정한다.
• -5/8 신호의 부분 주파수가 +5/8인 정도를 측정한다.
• -3/4 신호의 부분 주파수가 +3/4인 정도를 측정한다.
• -7/8 신호의 부분 주파수가 +7/8인 정도를 측정한다.

동등하게 마지막 행은 부분 주파수가 +1/8이고 따라서 신호의 부분 주파수가 -1/8인 정도를 측정할 수 있다. 이와 같이 매트릭스의 맨 위 행은 신호의 "측정" 양의 주파수 성분을, 맨 아래 행은 신호의 음의 주파수 성분을 측정한다고 할 수 있다.

유니터리 변환

DFT는 (또는 적절한 스케일 선택을 통해) 단일 변환, 즉 에너지를 보존하는 변환이다. 단위성을 달성하기 위한 적절한 스케일링 선택은 1${\displaystyle /N\sqrt{}}$ ${\$이므로 물리적 영역의 에너지는 푸리에 영역의 에너지와 동일하며, 즉 파르세발(Parseval)의 정리를 만족시킨다.(기타, 비통일성, 메스팅도 계산 편의상 일반적으로 사용된다. 예: 콘볼루티오)n 정리는 이산 푸리에 변환 글에 나타난 스케일링으로 약간 단순한 형태를 취한다.)

기타 속성

고유값, 경련 연결, 응용 프로그램 등을 포함한 DFT 매트릭스의 다른 속성은 이산 푸리에 변환 문서를 참조하십시오.

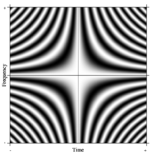
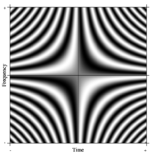
제한 사례: 푸리에 연산자

푸리에 변환의 개념은 쉽게 일반화된다. 그러한 N 포인트 DFT의 공식화 중 하나는 N을 임의로 크게 취함으로써 상상할 수 있다. 한계에 있어서, 엄격한 수학 기계는 그러한 선형 연산자를 소위 적분 변환으로 취급한다. 이 경우 행에 복잡한 지수(즉, 코사인 실재 부분과 사인 가상 부분)가 있는 매우 큰 행렬을 만들어 바운드 없이 분해능을 높이면, 제2종 프레드홀름 적분 방정식의 커널, 즉 연속 푸리에 변환을 정의하는 푸리에 연산자에 접근한다. 이 연속 푸리에 연산자의 직사각형 부분은 오른쪽에 보이는 것처럼 DFT 매트릭스와 유사한 이미지로 표시될 수 있다. 여기서 그리스케일 픽셀 값은 숫자 양을 나타낸다.

참고 항목

• 다차원 변환
• 시계 및 시프트 행렬

참조

• P. C.Yip, K. Ramamohan Rao에 의한 변환 및 데이터 압축 핸드북 – 주로 DFT 매트릭스를 기반으로 한 DFT 처리에 대해서는 제2장 참조

외부 링크

위키미디어 커먼스는 DFT 매트릭스와 관련된 미디어를 보유하고 있다.

• 푸리에 연산자 및 소멸 시간(DIT)