오일러의 회전 정리

오일러 축과 각도로 대표되는 회전.

기하학에서 오일러의 회전 정리는 3차원 공간에서 강체 신체의 한 지점이 고정된 상태를 유지하도록 하는 강체 신체의 어떤 변위는 고정점을 통과하는 어떤 축을 중심으로 한 하나의 회전과 동등하다고 기술하고 있다.또한 두 개의 회전 구성도 회전이라는 것을 의미한다.따라서 회전 집합은 회전 집단이라고 알려진 그룹 구조를 가지고 있다.

이 정리는 1775년 구면 기하학을 이용하여 증명했던 레온하르트 오일러의 이름을 따서 명명되었다.회전축은 오일러 축으로 알려져 있으며, 일반적으로 단위 벡터 $vector$ 으로 표현된다.회전각에 의한 그것의 제품은 축각 벡터라고 알려져 있다.정리가 운동학으로 확장되면 순간 회전 축의 개념, 즉 고정된 점의 선이 나온다.

선형 대수학 용어에서, 정리는 3D 공간에서 공통 원점을 가진 두 개의 카르테시안 좌표계가 어떤 고정 축에 대한 회전에 의해 연관되어 있다고 기술한다.이것은 또한 두 회전 행렬의 곱이 다시 회전 행렬이고 비식별 회전 행렬의 경우 한 고유값은 1이고 나머지 두 값은 둘 다 복잡하거나 둘 다 -1과 같다는 것을 의미한다.이 고유값에 해당하는 고유 벡터는 두 시스템을 연결하는 회전 축이다.

오일러의 정리(1776년)

오일러는 정리를 다음과 같이 말한다.^[1]

정리.quomodocunque sphaera circa centrum conuertatur, semper assignari potest 직경, 상황 반투명 cuius directio in sittranato conueniat cum initi.

또는 (영어):

구가 중심 주위를 움직일 때, 이동된 위치의 방향이 초기 위치와 동일한 직경을 항상 찾을 수 있다.

그림 1:

O

를 통해 직경을 중심으로 회전할 때 구체의 파란색 원은 빨간색 원 모양으로 변한다.

증명

오일러의 원래 증거는 구면 기하학을 사용하여 만들어졌기 때문에 삼각형에 대해 말할 때마다 구면 삼각형으로 이해되어야 한다.

이전분석

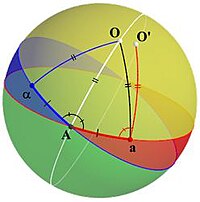
어떤 증거에 도달하기 위해 오일러는 만약 정리가 사실이라면 상황이 어떤 모습일지 분석한다.이를 위해 그림 1의 노란색 선이 구의 중심을 통과하여 우리가 찾고 있는 회전축이며, 점 $O$ 는 구와 그 축의 두 교차점 중 하나라고 가정한다.그리고는 $O$ (파란색 원)를 포함하지 않는 임의의 큰 원과 회전 후의 그 이미지(빨간색 원)를 고려하는데, 이것은 $O$ 를 포함하지 않은 또 하나의 큰 원이다.그는 그들의 교차로에 점 $A$ 를 점 A로 표시한다. (만약 원들이 일치한다면, $A$ 는 어느 쪽이든 점으로 간주될 수 있다. 그렇지 않으면 $A$ 는 두 교차로 중 하나이다.)

그림 2:

사전

이미지

α

및

이미지

A

를

A

에서 각도의 이등분자 AO와 연결하는 아크.

이제 $A$ 는 초기 원(파란색 원)에 있으므로 그 이미지는 전송된 원(빨간색)에 있을 것이다.그는 그 이미지를 점 $a$ 라고 부른다. $A$ 도 전송된 원(빨간색)에 있기 때문에, 초기 원(파란색)에 있던 또 다른 점의 이미지인데, 그는 프리이미지를 $α$ 로 표시한다(그림 2 참조).그런 다음 그는 두 호가 $α$ 와 $A$ 와 결합하는 것을 고려한다.이 $호들$ 은 호 αA가 호 $Aa$ 에 매핑되기 때문에 길이가 같다.또한 $O$ 는 고정점이기 때문에 삼각형 $αOA$ 는 삼각형 $AOA$ 에 매핑되므로 이 삼각형은 이소셀이며, 호 $AO$ 는 각 $αAa$ 를 이등분한다.

그림 3:

O

는

O

로

가지만

O

는

O와 일치해야 한다.

최적 후보지 구축

이전의 고려사항으로 불변할 수 있는 점을 구성하자.우리는 파란색 원과 그것의 이미지로부터 시작하는데, 그것은 그림 1과 같이 빨간색 원이다. $A점$ 을 그 원들의 교차점이 되게 하자.변환 중인 $A$ 의 이미지가 같은 점이라면 $A$ 는 변환의 고정점이고, 중심도 고정점이기 때문에 $A$ 를 포함하는 구의 직경은 회전축이며 정리도 증명된다.

그렇지 않으면 우리는 $A$ 의 이미지를 $a$ 로, 그리고 그 전상을 $α$ 로 표시하고, 이 두 점을 arcs $αA$ 와 $Aa$ 로 $A$ 에 연결한다.이 호들은 길이가 같다. $∠$ $αAa$ 를 이등분하는 큰 원을 구성하고 그 큰 원 위에 점 $O$ 를 위치시켜 호 $AO$ 와 $AO$ 의 길이가 같도록 하고, O를 포함하는 구의 $영역$ 을 $redαAa$ 의 내부로 부른다.(그림 3의 황색 영역)그러면 $αA$ = $Aa$ 와 $O$ 가 $αAa$ 의 이등분자 위에 있기 때문에 $αO$ = $aO$ 도 있다.

변환 시 비침투성의 증거

$이제$ O $'$ 이 $O$ 의 이미지라고 가정해 보자.그러면 우리는 $ααAO$ = $aaAaO'$ 과 방향은 보존되어 있으므로 $O'$ 은 $ααAa$ 의 내부여야 한다.^[a]이제 $AO$ 는 $AO$ 로 변환되므로 $AO$ = $AO'.$ $AO$ 도 $AO$ 와 길이가 같기 때문에 $∠ AaO$ = $∠ AO$ 이다.그러나 $∠ AO$ = $∠ AaO',$ 따라서 $aaAaO$ $= aaAaO',$ $따라서$ O $'$ 은 $O$ 와 같은 지점이다.즉 $O$ 는 변형의 고정점이고, 중심도 고정점이기 때문에 $O$ 를 포함하는 구의 직경은 회전축이다.

시공에 대한 최종 참고 사항

오일러의 원래 그림

오일러는 또한, 실제로 보다 용이할 수 있는 공사인 $∠ αAO$ 의 각도 이등분자와 $AA$ 의 수직 이등분선을 교차시켜 $O$ 를 찾을 수 있다고 지적한다.그는 또한 다음과 같은 두 가지 비행기의 교차점을 제안했다.

$∠ αAa$ (구체의 중심 $C$ 를 통과하는 각도)의 대칭 평면 및
호 $Aa$ 의 대칭면( $C$ 를 통과하기도 한다.

제안.이 두 평면은 직경으로 교차한다.이 직경이 우리가 찾고 있는 직경이다.

증명.

O

에게 구면 위에 이 지름이 두 개 있는 끝점 중 하나를 호출하자.

αA

는

Aa

에 지도되어 있고 삼각형은 동일한 각도를 가지기 때문에,

삼각형

OAA

로 이송되는 것을 따른다.

따라서

O 지점은 이동 중에 고정되어 있어야 한다.

코롤러리.이것은 또한 구의 회전을 위에서 설명한 두 평면에 대한 연속적인 반사로 볼 수 있음을 보여준다.거울 평면의 점들은 반사하에서는 불변성이며, 따라서 교차점(선: 회전축)의 점들은 반사하에서는 불변성이며, 따라서 회전하에서는 불변성이 된다.

회전축을 찾는 또 다른 간단한 방법은 점 $α$ , $A$ 가 $거짓말$ 인 평면을 고려하는 것이다.회전축은 분명히 이 평면에 직교하며 구의 중심 $C$ 를 통과한다.

경직된 신체의 경우 축 불변성을 남기는 모든 움직임이 회전이라는 점을 고려할 때, 이것은 또한 임의의 회전 구성이 새로운 축을 중심으로 한 단일 회전과 동일하다는 것을 증명한다.

매트릭스 프루프

공간 회전은 좌표 벡터 $X$ 를 $X$ , 즉 $Rx$ = $X$ 로 변환하는 3 × 3 회전 행렬 $R$ 과 일대일 대응의 선형 지도다.따라서 오일러 정리의 다른 버전은 모든 회전 $R$ 에 대해 $Rn$ = $n$ 인 비제로 벡터 $n$ 이 있다는 것이다. 이는 정확히 $n$ 이 고유값 1과 연관된 $R$ 의 고유 벡터라는 주장이다.따라서 1이 $R$ 의 고유값임을 입증하기에 충분하며, $R$ 의 회전 축은 선 $μn$ 이 되며 여기서 $n$ 은 고유값 1을 갖는 고유 벡터다.

회전 행렬은 그것의 역이 그것의 전치(transpose)라는 근본적인 속성을 가지고 있다.

\mathbf {R} ^{\mathsf {T}\mathbf {R} \mathbf {R} \mathbf {R} ^{\mathsf {T}=\mathbf {I},

여기서 $나$ 는 3 × 3 아이덴티티 매트릭스이고 위첨자 T는 전치 매트릭스를 나타낸다.

회전 행렬에 결정 인자가 ±1이라는 것을 찾기 위해 이 관계의 결정 인자를 계산한다.특히.

{\begin}1=\det(\mathbf {I} )&=\det(\mathbf {R} ^{\mathsf {T}\mathbf {R} \right)=\\det \det(\mathbf {R}^{\mathsf {T}\right)\det(\mathbf {R} )=\det(\mathbf {R}^{2}\\Longrightarrow \qquad \det(\mathbf {R})&=\pmpmpm)1.\end{정렬}}

결정인자 +1이 있는 회전 행렬은 적절한 회전이고, 음의 결정인자 -1이 있는 회전 행렬은 부적절한 회전이며, 이는 적절한 회전과 결합된 반사율이다.

이제 적절한 회전 행렬 $R$ 에 적어도 하나의 불변 벡터 $n$ , 즉 $Rn$ = $n$ 이 있다는 것을 알 수 있을 것이다. 이것은 ( $R$ - I $) n$ = $0$ 이 필요하기 때문에, $벡터$ n은 고유값 $λ$ = $1$ 을 갖는 $행렬$ R의 고유 벡터여야 한다.따라서 이는 $det(R$ - I $)$ = $0임$ 을 보여주는 것과 같다.

두 관계 사용

\det(-\mathbf {A} )=-1^{3}\det(\mathbf {A} )=-\det(\mathbf {A} )\quad

3 × 3 행렬 A에 대해

\det \left(\mathbf {R} ^{-1}\right)=1\quad

( $det(R)$ = $1$ )을 계산할 때

{\begin}&\det(\mathbf {R} -\mathbf {I})=\det \det(\mathbf {R} -\mathbf {I} )^{\mathsf {T}\right)\\\\\\\{}={}&\det \left(\mathbf {R}) ^{\mathsf {T}-\mathbf {I} \right)=\det \left(\mathbf {R} ^{-1}-\mathbf {R} ^{-1}\mathbf {R} \right)\\\{}={}&\det \left(\mathbf {R}) ^{-1}(\mathbf {I} -\mathbf {R} )\오른쪽)=\\det \det(\mathbf {R}^{-1}\right)\\\\det(-\mathbf {R} -\mathbf {I})\}\{}={}&-\det(\mathbf {R} -\mathbf {I}\\\\\t]\Longrightarrow \ 0={}&\det(\mathbf {R} -\mathbf {I}).\end{정렬}}

이는 $λ$ = $1$ 이 특성 방정식의 루트(솔루션)라는 것을 보여준다.

\det(\mathbf {R} -\lambda \mathbf {I})=0\quad {\hbox{for}\quad \lambda =1.

즉, $매트릭스 R$ - I는 단수이고 0이 아닌 커널을 가지고 있다, 즉 $n$ 이라고 하는 적어도 하나의 0이 아닌 벡터가 있다.

{\displaystyle(\mathbf {R} -\mathbf {I} )\mathbf {n} =\mathb {0} \quad \Long 왼쪽 오른쪽arrow \quad \mathbf {R} \mathbf {n} =\mathbf {n}.}}

실제 $μn$ 에 대한 선 $μn$ 은 $R$ 에서 불변성, 즉 $μn$ 은 회전축이다.이것은 오일러의 정리를 증명한다.

직교 행렬과 회전 행렬의 동등성

두 행렬(선형 지도를 나타냄)은 한 행렬이 다른 행렬과 같게 만드는 근거의 변경이 있을 경우 등가라고 한다.적절한 직교 행렬은 항상 다음 행렬 또는 수직 반사와 동일하다(이러한 의미).

{\displaystyle \mathbf {R} \sim {\begin{pmatrix}\cos \pi &-\sin \phi&\\cos \phi &\cos \phi &0\0&0&1\end{pmatrix}},\quad 0\leq \leq \leq \leq \leq \leq \leq \leq \leq \leq \leq \leq 2\pi .

그러면 직교 행렬은 회전 또는 부적절한 회전이다.일반 직교 행렬에는 +1 또는 -1 중 하나의 실제 고유값이 있을 뿐이다.+1일 때 행렬은 회전이다.-1일 경우 행렬은 부적절한 회전이다.

$R$ 에 둘 이상의 불변 벡터가 있으면 $φ$ = 0, $R$ = $I$ . 임의 벡터는 $I$ 의 불변 벡터다.

행렬 이론으로의 이동

이전의 방정식을 증명하기 위해서는 매트릭스 이론의 일부 사실들이 상기되어야 한다.

$m$ × $m$ 행렬 $A$ 는 $A$ 가 정상인 경우에만, 즉 $AA$ 가^†AA일 $경우$ 에만^† $m$ 직교 고유 벡터를 가진다.^[b]이 결과는 단일 유사성 변환에 의해 일반 행렬을 대각선 형태로 가져올 수 있다고 말하는 것과 같다.

\mathbf {A} \mathbf {U} =\mathbf {U} \;\operatorname {diag} (\alpha _{1},\ldots ,\alpha _{m})\quad \Longleftrightarrow \quad \mathbf {U} ^{\dagger }\mathbf {A} \mathbf {U} =\operatorname {diag} (\alpha _{1},\ldots ,\alpha _{m}),

$그리고$ U는 단일하수체, 즉,

\mathbf {U} ^{\daugger }=\mathbf {U} ^{-1}.

고유값 $α 1, ...,$ $α$ 는_m 특성 방정식의 뿌리다.행렬 $A$ 가 단일 행렬인 경우(그리고 단일 행렬이 정상이라는 점에 유의),

\left(\mathbf {U} ^{\dagger }\mathbf {A} \mathbf {U} \right)^{\dagger }=\operatorname {diag} \left(\alpha _{1}^{*},\ldots ,\alpha _{m}^{*}\right)=\mathbf {U} ^{\dagger }\mathbf {A} ^{-1}\mathbf {U} =\operatorname {diag} \left({\frac {1}{\alpha _{1}}},\ldots ,{\frac {1}{\alpha _{m}}}\right)

그리고 그것은 복잡한 평면에서 단일 행렬의 고유값이 단위 원에 있다는 것을 따른다.

\alpha _{k}^{*}={\frac {1}{\nalpha _{k}}}\quad \long leftrikrightarrow \quad \quad \quad \{k}^{k}}}}\long \long \alpha \lapha \{quarroward \{quad \{quarroward \{quarroward \{quarroworda \{1

또한 직교(실제 단일) 행렬은 복잡한 평면의 단위 원에 고유값을 가진다.더욱이 그것의 특성 방정식( $λ$ 의 m번째 순서 다항식)은 실제 계수를 가지기 때문에, 그 뿌리는 복잡한 결합 쌍으로 나타나는데, 즉, $α$ 가 뿌리라면 $α$ 가^∗ 된다.뿌리는 3개가 있으므로 적어도 하나는 순전히 진짜(+1 또는 -1)여야 한다.

매트릭스 이론에서 이러한 일반적인 사실들을 기억해낸 후, 우리는 회전 매트릭스 $R$ 로 돌아간다.U를 찾을 수 있다는 것은 그 실재성과 직교성으로부터 다음과 같은 $U$ 를 찾을 수 있다.

\mathbf {R} \mathbf {U} =\mathbf {U} {\begin{pmatrix}e^{i\0&0&0\0\e^{-i\pmatrix}}

만약 위의 형식을 주는 행렬 $U$ 가 발견될 수 있고, 순수하게 실제적인 구성요소가 하나 있을 뿐이고 그것이 -1이라면, 우리는 R을 부적절한 회전이라고 정의한다.그렇다면 적절한 회전(제3의 고유값은 1에 불과함)인 행렬 R의 사례만 고려해보자.그러면 3 × 3 행렬 $U$ 의 세 번째 열은 불변 벡터 $n$ 과 같게 된다. $U$ 의 처음 두 열에 $u$ 와₁ $u$ 를₂ 쓰면서, 이 방정식은

\mathbf {R} \mathbf {u} _{1}=e^{i\phi }\,\mathbf {u} _{1}\quad {\hbox{and}}\quad \mathbf {R} \mathbf {u} _{2}=e^{-i\phi }\,\mathbf {u} _{2}.

$u$ 에₁ 고유값 1이 있으면 $φ$ = $0$ 이고 $u$ 에도₂ 고유값 1이 있는데, 이는 이 경우 $R$ = $E$ 를 의미한다.

마지막으로, 행렬 방정식은 단일 행렬을 통해 변환된다.

\mathbf{R}\mathbf{U}{\begin{pmatrix}{\frac{1}{\sqrt{2}}}&{\frac{나는}{\sqrt{2}}}&0\\{\frac{1}{\sqrt{2}}}&{\frac{-i}{\sqrt{2}}}&0\\0&, 0&, 1\\\end{pmatrix}}=\mathbf{U}\underbrace{{\begin{pmatrix}{\frac{1}{\sqrt{2}}}&{\frac{나는}{\sqrt{2}}}&0\\{\frac{1}{\sqrt{2}}}&{\frac{-i}{\sqrt{2}}}&a.융점, 0\\0&, 0&, 1\\\end{pmatrix}}{\begin{pmatrIx}{\frac{1}{\sqrt{2}}}&{\frac{1}{\sqrt{2}}}&0\\{\frac{-i}{\sqrt{2}}}&{\frac{나는}{\sqrt{2}}}&0\\0&, 0&, 1\\\end{pmatrix}}}_{=\, \mathbf{나는}}{\begin{pmatrix}e^{i\phi}&, 0&, 0\\0&, e^{-i\phi}&, 0\\0&, 0&, 1\\\end{pmatrix}}{\begin{pmatrix}{\frac{1}{\sqrt{2}}}&{\frac{나는}{\sqrt{2}}}&0\\{\frac{1}{\sqrt.{2}}}&{\frac{-i}{\sqrt{2}}}&0\\0&, 0&, 1\\\end{pmatrix}}

어떤 것을 주는지

\mathbf{U의}^{\dagger}\mathbf, 1\\\end{pmatrix}}\quad{\text{과}}\quad\mathbf{U의}=\mathbf{U}{\begin{pmatrix}{\frac{1}{\sqrt{2}}}&{\frac{나는}{\sqrt{2}}}&0\\{\frac{1}{\sqrt{2}}}&{\frac{-i}{\sqrt{2{U의}={\begin{pmatrix}\cos\phi&-\sin \phi&0\\\sin \phi&\cos \phi&0\\0&, 0& \mathbf{R}.}}}&0\\0&, 0&, 1\\\end{pmatrix}}.

$U'$ 의 기둥은 정형이다.세 번째 열은 여전히 $n$ 이고, 나머지 두 열은 $n$ 에 수직이다.우리는 이제 부적절한 회전에 대한 우리의 정의가 기하학적 해석과 어떻게 일치하는지 알 수 있다: 부적절한 회전은 축을 중심으로 한 회전(여기서, 세 번째 좌표에 해당하는 축)과 그 축에 수직인 평면에 대한 반사를 말한다.만약 우리가 결정인자 1을 가진 행렬로만 제한한다면, 우리는 그것들이 적절한 회전이어야 한다는 것을 알 수 있다.이 결과는 적절한 회전에 해당하는 직교 행렬 $R$ 은 축 $n$ 을 중심으로 한 각도 $φ$ 에 걸친 회전에 해당함을 의미한다.

등가 등급

위에 주어진 실제 회전 행렬의 트레이스(대각선 원소의 합계)는 1 + 2 $cos$ $φ$ 이다.직교 행렬 유사성 변환에서는 트레이스가 불변하므로,

\mathrm {Tr} \left[\mathbf {A} \mathbf {R} \mathbf {A} ^{\mathsf {T}}\right]=\mathrm {Tr} \left[\mathbf {R} \mathbf {A} ^{\mathsf {T}}\mathbf {A} \right]=\mathrm {Tr} [\mathbf {R} ]\quad {\text{ with }}\quad \mathbf {A} ^{\mathsf {T}}=\mathbf {A} ^{-1},

이러한 직교 매트릭스 변환에 의해 $R$ 과 동등한 모든 행렬은 동일한 트레이스를 가지고 있다: 트레이스는 클래스 함수다.이 행렬 변환은 명백히 동등성 관계, 즉 그러한 모든 등가 행렬이 동등성 등급을 형성한다.

실제로 모든 적절한 회전 3 × 3 회전 행렬은 그룹을 형성하며, 대개 SO(3)(3차원의 특수 직교 그룹)로 표시되며, 동일한 추적을 가진 모든 행렬은 이 그룹에서 동등성 등급을 형성한다.그러한 동등성 등급의 모든 요소는 회전 각도를 공유하지만, 모든 회전은 다른 축을 중심으로 한다. $n$ 이 고유값 1을 가진 $R$ 의 고유 벡터인 경우, $An$ 은 또한 $ARA$ 의^T 고유 벡터로서 고유값 1도 있다. $A$ = $I$ , $n$ 과 $An$ 이 다른 것이 아니라면.

적용들

회전 발전기

단위 벡터 $[x,$ $y,$ $z]$ 에 의해 회전 축을 지정하고, 그 벡터에 대해 각도 Δθ의 무한히 작은 회전이 있다고 가정하자.무한의 추가로서 회전 행렬을 확장하고, 첫 번째 순서 접근법을 취하면 회전 행렬 $ΔR$ 은 다음과 같이 표현된다.

\Delta R={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}+{\begin{bmatrix}0&z&-y\\-z&0&x\\y&-x&0\end{bmatrix}}\,\Delta \theta =\mathbf {I} +\mathbf {A} \,\Delta \theta .

이 축에 대한 각도 $θ$ 을 통한 유한 회전은 같은 축에 대한 작은 회전의 연속이라고 볼 수 있다..mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px로 Δθ Approximating. 어디 N은 큰 숫자 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}θ/N, θ의 축에 대한 회전:표시할 수 있다.

R=\왼쪽(\mathbf {1} +{\frac {\mathbf {A} \theta }{N}\오른쪽)^{N}\ 관련 e^{\mathbf {A} \theta }

오일러의 정리는 모든 회전이 이 형태로 표현될 수 있다고 본질적으로 기술하고 있음을 알 수 있다.제품 $Aθ$ 는 매트릭스 $A$ 와 관련된 벡터 $(x, y, z)$ 가 되는 특정 회전의 "제너레이터"이다.이는 회전 행렬과 축 각도 형식이 지수 함수에 의해 연관되어 있음을 보여준다.

발전기 $G$ 에 대한 간단한 표현을 도출할 수 있다.한 쌍의 수직 단위 벡터 $a$ 와 $b$ 에 의해 정의된 임의 평면(유클리드 공간에서)으로 시작한다.이 평면에서는 수직 $y$ 를 갖는 임의 벡터 $x$ 를 선택할 수 있다.그런 다음 $x$ 의 $관점$ 에서 y를 해결하며 평면에서 회전을 위한 표현으로 대체하면 제너레이터 $G$ = $ba$ ^T - $ab$ 을^T 포함하는 회전 행렬 $R$ 을 산출한다.

{\displaystyle{\begin{정렬}\mathbf{)}&=\mathbf{를}\cos \alpha +\mathbf{b}\sin \alpha \\\mathbf{y}&=-\mathbf{를}\sin \alpha +\mathbf{b}\cos\alpha \\[8pt]\cos \alpha&=\mathbf{를}^{\mathsf{T}};=\mathbf{b}^{\mathsf{T}}{)}\\[8px]\mathbf{y}및 \mathbf, =-\mathbf{농양}^{\mathsf{T}}\mathbf{)}\\\sin \alpha 및 \mathbf. {)}+\mathbf{영혼}^{\mathsf{T}}\\[8px]\mathbf{)}'&{)}, =\mathbf{)}\cos \beta +\mathbf{y}\sin \beta \\&, =\left((\mathbf{영혼}^{\mathsf{T}}-\mathbf{에어로빅}^{\mathsf{T}}\mathbf{나는}\right\beta +\left \cos)\sin\beta \right)\mathbf{)}\\[8px]\mathbf{R}&=\mathbf{나는}{)}=\left(\mathbf{영혼}^{\mathsf{T}}-\mathbf{에어로빅}^{\mathsf{T}}\right)\mathbf \mathbf.\cos \beta+\left(\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\right)\sin \beta \\&=\mathbf {I} \cos \beta +\mathbf {G} \sin \beta \\[8px]\mathbf {G} &=\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\end{aligned}}}

회전 시 평면 외부에 벡터를 포함하려면 공간을 분할하는 두 개의 투영 연산자를 포함하여 위의 $R$ 식을 수정할 필요가 있다.이 수정된 회전 행렬은 지수 함수로 다시 쓸 수 있다.

{\begin{aligned}\mathbf {P_{ab}} &=-\mathbf {G} ^{2}\\\mathbf {R} &=\mathbf {I} -\mathbf {P_{ab}} +\left(\mathbf {I} \cos \beta +\mathbf {G} \sin \beta \right)\mathbf {P_{ab}} =e^{\mathbf {G} \beta }\end{aligned}}

분석은 종종 전체 회전 행렬보다 이러한 발전기의 측면에서 더 쉽다.발전기 측면에서 분석은 회전 그룹의 Lie 대수라고 알려져 있다.

쿼터니온스

어떤 좌표계 쌍의 상대적 방향은 세 개의 독립된 숫자의 집합에 의해 지정될 수 있다는 것은 오일러의 정리로부터 따른다.때때로 쿼터니온 대수학으로 연산을 단순화하기 위해 중복된 네 번째 숫자가 추가된다.이 숫자 중 3개는 고유 벡터를 향하는 방향 코사인이다.네 번째는 두 개의 좌표를 구분하는 고유 벡터에 대한 각도다.이런 네 개의 숫자 집합을 쿼터니온이라고 한다.

위에서 설명한 쿼터니온은 복잡한 숫자들을 포함하지 않지만, 만약 쿼터니온이 두 번의 연속 회전을 설명하기 위해 사용된다면, 그것들은 윌리엄 로완 해밀턴에 의해 도출된 비확정 쿼터니온 대수학을 사용하여 결합되어야 한다.

쿼터를 통한 회전 계산은 필요한 계산의 감소와 반올림 오류를 최소화하는 능력을 통해 항공우주 애플리케이션에서 방향 코사인의 사용을 대체하게 되었다.또한 컴퓨터 그래픽에서는 비교적 쉽게 쿼터니온들 사이의 구형 보간술을 수행할 수 있는 능력이 가치가 있다.

일반화

더 높은 치수에서 치수 $2n$ 또는 $2n$ + $1$ 의 점을 보존하는 강성 운동은 직교 회전의 평면에서 최대 n $회전$ 으로 구성된다. 단, 이러한 평면이 고유하게 결정될 필요는 없으며, 강성 운동이 복수의 축을 고정할 수 있다.

스크류 모션.

점을 반드시 고정하지 않는 3차원의 경직된 동작은 "스크루 동작"이다.그 이유는 축에 수직인 변환을 가진 회전 구성은 평행 축을 중심으로 한 회전인 반면 축에 평행한 변환을 가진 구성은 나사 움직임을 산출하기 때문이다. 나사 축을 참조한다.이것은 나사가론을 낳는다.

참고 항목

메모들

^ 방향은 $αA$ 가 $OA$ 에 맞춰 $A$ 를 반시계방향으로 회전할 경우, $AA$ 를 $반시계방향$ 으로 회전시켜 $O'a$ 에 맞춰야 한다는 의미에서 보존되어 있다.마찬가지로 회전이 시계방향이라면.
^ 단도 기호 $†$ 은 복잡한 결합에 이어 전치를 의미한다.실제 행렬의 경우 복잡한 결합은 아무 것도 하지 않으며 실제 행렬을 만드는 것은 그것을 바꾸는 것과 같다.

참조

^ 노비 코멘타리 학술원 사이언톨리움 페트로폴리타나에 20, 1776, 페이지 189–207 (E478)

본 기사는 Creative Commons Attribution-ShareAlike 3.0 Unported License에 따라 허가되었지만 GFDL에 따라 허가되지 않은 Citizensium 기사 "Uler의 정리(회전)"의 자료를 통합하고 있다.

오일러의 정리 및 그 증거는 L. 을레로 (Leonhard Euler)의 부록 (Additamentum. 페이지 201–203)의 24~26항에 수록되어 있으며, Formulae generales pro translatione quacunque componomerumorum (임의 강체 변환을 위한 일반 공식)이 성에게 제시되어 있다.Petersburg Academy on October 9, 1775, and first published in Novi Commentarii academiae scientiarum Petropolitanae 20, 1776, pp. 189–207 (E478) and was reprinted in Theoria motus corporum rigidorum, ed. nova, 1790, pp. 449–460 (E478a) and later in his collected works Opera Omnia, Series 2, Volume 9, pp. 84–98.
Palais, Bob; Palais, Richard; Rodi, Stephen (2009). "A Disorienting Look at Euler's Theorem on the Axis of a Rotation". American Mathematical Monthly. 116 (10): 892–909. doi:10.4169/000298909x477014.

외부 링크

오일러 아카이브의 오일러 원본 논문: E478에 기재, 1776년 첫 번째 간행물(pdf)
오일러의 원문(라틴어)과 영어 번역(요한 스텐)
오일러의 회전 정리를 위한 울프램 시연 프로젝트 (톰 베르호프)

[2] 방향은 $αA$ 가 $OA$ 에 맞춰 $A$ 를 반시계방향으로 회전할 경우, $AA$ 를 $반시계방향$ 으로 회전시켜 $O'a$ 에 맞춰야 한다는 의미에서 보존되어 있다.마찬가지로 회전이 시계방향이라면.

[3] 단도 기호 $†$ 은 복잡한 결합에 이어 전치를 의미한다.실제 행렬의 경우 복잡한 결합은 아무 것도 하지 않으며 실제 행렬을 만드는 것은 그것을 바꾸는 것과 같다.

[1] 노비 코멘타리 학술원 사이언톨리움 페트로폴리타나에 20, 1776, 페이지 189–207 (E478)

[1]

[a]

[b]

v t 레온하르트 오일러
작동하다	기계공 분석 인피니토럼의 인트로덕티오 칼쿨리 차등성 칼쿨리 적분 독일 공주에게 보내는 편지
개념 이론과 이론	오일러-라그랑주 방정식 오일러-로트카 방정식 오일러-마클라우린 공식 오일러-마루야마법 오일러-마스케로니 상수 오일러-포아송-다르복스 방정식 오일러-로드리게스 공식 오일러-트리코미 방정식 오일러의 연속 분수식 오일러의 임계 하중 오일러의 공식 오일러의 4제곱 아이덴티티 오일러의 정체 오일러 펌프 및 터빈 방정식 오일러의 회전 정리 오일러의 힘의 합계 추측 오일러의 정리 오일러 방정식(유체 역학) 오일러 함수 오일러법 오일러 수 오일러 번호(물리학) 오일러-베르누엘리 빔 이론
다른이들	네임스케이크 오일러 위원회 요한 오일러 요한 베르누이 (베르누이 가문) 게오르크 지셀 메리안 가문 바젤학교(수학)
카테고리

Search