스윙 앳우드의 기계
Swinging Atwood's machine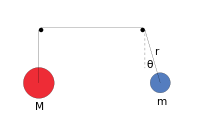
스윙하는 애트우드의 기계(SAM)는 질량 중 하나가 2차원 평면에서 스윙할 수 있다는 점을 제외하고는 단순한 애트우드의 기계와 유사한 메커니즘으로 일부 시스템 매개변수와 초기 조건에 대해 혼란스러운 동적 시스템을 생성합니다.
구체적으로, 진자가 균형추와 충돌하지 않고 풀리 주위에서 자유롭게 움직일 수 있도록 0 반경의 두 마찰 없는 풀리에 매달린 확장 불가능한 질량 없는 끈으로 연결된 두 개의 질량(진자, 질량 m 및 평형추, 질량 M)으로 구성됩니다.[1]
기존의 Atwood의 기계는 = m{\ = m을 제외하고 "진자" 솔루션(즉, 진자 또는 평형추가 결국 도르래와 충돌함)만을 허용합니다. 그러나, > m의 스윙하는 애트우드의 기계는 종료 또는 비종료, 주기적, 준주기적 또는 혼돈, 유계 또는 무한으로 분류될 수 있는 다양한 운동으로 이어지는 조건의 큰 매개변수 공간을 가지고 있습니다. 진자의 반응 원심력이 균형추의 무게를 상쇄하기 때문에 단수 또는 비 singular입니다. SAM에 대한 연구는 1982년 리드 칼리지의 니콜라스 투필라로(Nicholas Tufillaro)가 데이비드 J. 그리피스(David J. Griffiths)가 감독한 "Smiles and Teardrops(계의 일부 궤적의 모양을 지칭하는)"라는 제목의 선임 논문의 일부로 시작되었습니다.[3]
운동방정식

흔들리는 애트우드의 기계는 자유도가 2개인 시스템입니다. 우리는 해밀토니안 역학이나 라그랑지안 역학을 사용하여 운동 방정식을 유도할 수 있습니다. 스윙하는 m 스윙하지 않는 을 M 이라 하자 의 운동 에너지 T T는 다음과 같습니다.
여기서 r은 피벗까지의 스윙 질량의 거리이고,θ \theta}는 바로 아래를 가리키는 것에 대한 스윙 질량의 각도입니다. 위치 에너지 는 전적으로 중력에 의한 가속도 때문입니다.
그런 다음 의 라그랑지안 L 과 해밀턴 을 기록할 수 있습니다.
그런 다음 표준 운동량 θ {\displaystyle p_theta}}로 해밀턴을 표현할 수 있습니다.
라그랑주 분석을 적용하여 r 및θ {\displaystyle\theta}에서 두 개의 2차 결합 일반 미분 방정식을 얻을 수 있습니다.θdisplaystyle theta} 방정식은 다음과 같습니다.
r 방정식은 다음과 같습니다.
질량비 = displaystyle \mu = {\frac {M}{m}}을 정의하여 방정식을 단순화합니다. 그러면 위의 내용은 다음과 같습니다.
Hamiltonian 분석을 적용하여 θ \theta} 및 해당 표준 p p_{} p θ p_{\theta}의 관점에서 4개의 1차 ODE를 결정할 수도 있습니다.
이 두 파생 모델 모두에서θ {\displaystyle\theta} 및 θ ˙ theta}}를 0으로 설정하면 특수한 경우가 일반적인 스윙이 아닌 Atwood 기계입니다.
스윙하는 애트우드의 기계는 rθ displaystyle\theta} 및 해당 표준 p {\p_{} p θ p_{\theta }로 정의되는 4차원 위상 공간을 가지고 있습니다. 그러나 에너지 절약으로 인해 위상 공간은 3차원으로 제한됩니다.
거대한 도르래가 있는 시스템
시스템의 도르래에 관성 모멘트 및 R 이 있는 경우 SAM의 해밀토니안은 다음과 같습니다[4]
어디에 Mt 는 시스템의 유효 총 질량,
R 과( I {\displaystyle 이(가) 0이 되면 위 버전으로 줄어듭니다. 이제 운동 방정식은 다음과 같습니다.[4]
여기서 = / m {\displaystyle \mu _{t} = M_{t}/m}입니다.
통합성
해밀턴 시스템은 적분 가능한 것과 비적분 가능한 것으로 분류될 수 있습니다. μ = /m = {\displaystyle \mu = M/m = 3}일 때 SAM을 적분할 수 있습니다. 시스템도 = 2- 1 = 3, {\displaystyle \mu = 4n^{2}-1 = 3, 15, 35, ...에 대해 매우 규칙적으로 보입니다. 그러나 {\displaystyle \mu 3} 케이스가 유일하게 알려진 적분 가능한 질량 비율입니다. 은 ∈0, ∪, ∞)in(0, 1)\cup (3,\infty)}에 대해 통합할 수 없는 것으로 나타났습니다. 질량비의 다른 많은 값(및 초기 조건)에 대해 SAM은 혼돈 운동을 표시합니다.
수치 연구에 따르면 궤도가 단수일 때(initial 조건: =0, ˙ = v, θ = θ 0, θ ˙ 0 {\display r = 0, {\dot {r}} = v,\theta =\theta _{0}, {\dot {\theta}} = 0}, 진자가 하나의 대칭 루프를 실행하고 원점으로 돌아갑니다. θ {\displaystyle \theta _{0}}의 값에 관계없이. θ {\displaystyle \theta _{0}}이(수직에 가까운) 작을 때는 궤적이 "눈물 방울"을 설명하고 클 때는 "심장"을 설명합니다. 이러한 궤적은 대수적으로 정확히 해결될 수 있으며, 비선형 해밀턴이 있는 시스템에서는 이례적입니다.[7]
궤적
흔들리는 애트우드 기계의 요동하는 질량은 다른 초기 조건과 다른 질량 비율에 따라 흥미로운 궤적이나 궤도를 거칩니다. 여기에는 주기적 궤도와 충돌 궤도가 포함됩니다.
비특이궤도
특정 조건에서 시스템은 복잡한 고조파 운동을 나타냅니다.[1] 요동하는 질량이 도르래에 닿지 않으면 궤도를 비특이적이라고 합니다.
- = \mu = θ 0 = π 2 {\displaystyle \theta _{0} = {\frac {\pi }{2}}에 대한 스윙하는 애트우드 기계의 궤도 및 초기 속도가 0입니다.
- = \mu = 3 θ 0 = π 2 {\displaystyle \theta _{0} = {\frac {\pi }{2}}에 대한 스윙하는 애트우드 기계의 궤도 및 초기 속도가 0입니다.
- = \mu = 5 θ 0 = π 2 {\displaystyle \theta _{0} = {\frac {\pi }{2}}에 대한 스윙하는 애트우드 기계의 궤도 및 초기 속도가 0입니다.
- = \mu =6 θ 0 = π 2 {\displaystyle \theta _{0} = {\frac {\pi }{2}}에 대한 스윙하는 애트우드 기계의 궤도 및 초기 속도가 0입니다.
- = \mu = 16 θ 0 = π 2 {\displaystyle \theta _{0} = {\frac {\pi }{2}}에 대한 스윙하는 애트우드 기계의 궤도 및 초기 속도가 0입니다.
- = \mu = 19 θ 0 = π 2 {\displaystyle \theta _{0} = {\frac {\pi }{2}}에 대한 스윙하는 애트우드 기계의 궤도 및 초기 속도가 0입니다.
- = \mu = 21 θ 0 = π 2 {\displaystyle \theta _{0} = {\frac {\pi }{2}}에 대한 스윙하는 애트우드 기계의 궤도 및 초기 속도가 0입니다.
- = \mu = 24 θ 0 = π 2 {\displaystyle \theta _{0} = {\frac {\pi }{2}}에 대한 스윙하는 애트우드 기계의 궤도 및 초기 속도가 0입니다.
주기궤도

시스템의 서로 다른 고조파 성분이 위상에 있을 때 생성된 궤적은 일반 진자와 유사한 "미소" 궤적과 다양한 루프와 같이 단순하고 주기적입니다.[3][8] 일반적으로 주기적인 궤도는 다음을 만족할 때 존재합니다.[1]
주기적 궤도의 가장 단순한 경우는 투필라로가 1984년 논문에서 A형 궤도라고 이름 붙인 "미소" 궤도입니다.[1]
- = 665 {\\mu = 1.665}, θ 0 = π 2 {\displaystyle \theta _{0} = {\frac {\pi }{2}}에 대한 스윙하는 애트우드 기계의 "smile" 궤도 및 초기 속도가 0입니다.
- = \mu = 2.}, θ 0 = π 2 {\displaystyle \theta _{0} ={\frac {\pi }{2}}에 대한 스윙하는 애트우드 기계의 궤도 및 초기 속도가 0입니다.
- = \mu = 1.1727}, θ 0 = π 2 {\displaystyle \theta _{0} ={\frac {\pi }{2}}, 초기 속도 0에 대한 Atwood 기계의 궤도.
- = \mu = 1.555}, θ 0 = π 2 {\displaystyle \theta _{0} = {\frac {\pi }{2}}, 초기 속도 0에 대한 Atwood 기계의 궤도.
특이궤도
만약 어느 시점에서 요동하는 질량이 원점을 통과한다면 그 움직임은 특이합니다. 시스템은 시간 역전과 번역 하에서 불변이므로 진자가 원점에서 시작하여 바깥쪽으로 발사된다고 하는 것과 같습니다.[1]
{\ 이 0에 가깝고 운동 방정식을 r로 나누어야 하므로 피벗에 가까운 영역은 단수입니다 따라서 이러한 경우를 엄격하게 분석하려면 특수한 기술을 사용해야 합니다.[9]
다음은 임의로 선택된 단일 궤도의 도표입니다.
충돌궤도
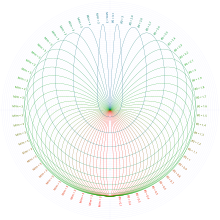
충돌(또는 끝나는 단수) 궤도는 요동하는 질량이 피벗에서 초기 속도로 분출되어 피벗으로 되돌아갈 때 형성되는 단수 궤도의 하위 집합입니다.
충돌 궤도 중 가장 단순한 경우는 질량비가 3인 궤도로 원점에서 분출된 후 항상 원점과 대칭적으로 되돌아오는 형태로 투필라로의 초기 논문에서 B형 궤도라고 이름 지었습니다.[1] 그것들은 또한 그들의 외모 때문에 눈물방울, 심장 또는 토끼 귀 궤도라고 불립니다.[3][7][8][9]
스윙하는 질량이 원점으로 돌아오면 균형추 인 M 이(가) 순간적으로 방향을 바꾸어 연결 문자열에 무한한 장력을 발생시킵니다. 따라서 우리는 지금 종료 동의를 고려할 수 있습니다.[1]
유계성
초기 위치의 경우 요동하는 질량은 원뿔형 단면인 곡선에 의해 경계지어짐을 알 수 있습니다.[2] 피벗은 항상 이 경계 곡선의 초점입니다. 이 곡선의 방정식은 계의 에너지를 분석하고 에너지 보존을 사용하여 유도할 수 있습니다. m이 r = r = r_ 및 θ θ 0 {\displaystyle \theta =\theta _{0}의 정지 상태에서 해제되었다고 가정합니다. 따라서 시스템의 총 에너지는 다음과 같습니다.
그러나 경계의 경우 요동하는 질량의 속도가 0임을 유의하십시오.[2] 그래서 우리는 다음과 같은 것을 가지고 있습니다.
원뿔 단면의 방정식임을 확인하기 위해 에 대해 다음과 같이 분리합니다
이 경우 분자는 초기 조건을 정지 상태로 가정했기 때문에 초기 위치에만 의존하는 상수입니다. 그러나 에너지 상수 는 0이 아닌 초기 속도에 대해서도 계산할 수 있으며, 이 식은 모든 경우에 여전히 유지됩니다.[2] 원뿔 단면의 편심은 입니다 > 의 경우 이것은 타원이며, 시스템은 경계를 이루고 요동하는 질량은 항상 타원 내에 유지됩니다. = {\ = 1}의 경우 포물선이고 μ < 1 {\displaystyle \mu < 1}의 경우 쌍곡선이며, 이 두 경우 모두 경계가 아닙니다. 가 임의로 커짐에 따라 경계 곡선이 원에 접근합니다. 곡선으로 둘러싸인 지역은 힐스 지역으로 알려져 있습니다.[2]
최근 3차원 확장
2016년에 3차원 스윙 앳우드 머신(3D-SAM)의 문제에 대한 새로운 통합 사례가 발표되었습니다.[10] 2D 버전과 마찬가지로 는 M = displaystyle M = 3m}일 때 통합 가능합니다.
참고문헌
- ^ a b c d e f g h i Tufillaro, Nicholas B.; Abbott, Tyler A.; Griffiths, David J. (1984). "Swinging Atwood's Machine". American Journal of Physics. 52 (10): 895–903. Bibcode:1984AmJPh..52..895T. doi:10.1119/1.13791.
- ^ a b c d e Tufillaro, Nicholas B.; Nunes, A.; Casasayas, J. (1988). "Unbounded orbits of a swinging Atwood's machine". American Journal of Physics. 56: 1117. Bibcode:1988AmJPh..56.1117T. doi:10.1119/1.15774.
- ^ a b c Tufillaro, Nicholas B. (1982). Smiles and Teardrops (Thesis). Reed College.
- ^ a b Pujol, Olivier; Perez, J.P.; Simo, C.; Simon, S.; Weil, J.A. (2010). "Swinging Atwood's Machine: Experimental and numerical results, and a theoretical study". Physica D. 239 (12): 1067–1081. arXiv:0912.5168. Bibcode:2010PhyD..239.1067P. doi:10.1016/j.physd.2010.02.017.
- ^ Tufillaro, Nicholas B. (1986). "Integrable motion of a swinging Atwood's machine". American Journal of Physics. 54 (2): 142. Bibcode:1986AmJPh..54..142T. doi:10.1119/1.14710.
- ^ Casasayas, J.; Nunes, A.; Tufillaro, N. (1990). "Swinging Atwood's Machine : integrability and dynamics". Journal de Physique. 51 (16): 1693–1702. doi:10.1051/jphys:0199000510160169300. ISSN 0302-0738.
- ^ a b Tufillaro, Nicholas B. (1994). "Teardrop and heart orbits of a swinging Atwoods machine,". American Journal of Physics. 62 (3): 231–233. arXiv:chao-dyn/9302006. Bibcode:1994AmJPh..62..231T. doi:10.1119/1.17602.
- ^ a b Tufillaro, Nicholas B. (1985). "Motions of a swinging Atwood's machine". Journal de Physique. 46 (9): 1495–1500. doi:10.1051/jphys:019850046090149500.
- ^ a b Tufillaro, Nicholas B. (1985). "Collision orbits of a swinging Atwood's machine" (PDF). Journal de Physique. 46: 2053–2056. doi:10.1051/jphys:0198500460120205300.
- ^ Elmandouh, A.A. (2016). "On the integrability of the motion of 3D-Swinging Atwood machine and related problems". Physics Letters A. 380: 989. Bibcode:2016PhLA..380..989E. doi:10.1016/j.physleta.2016.01.021.
더보기
- 알메이다, M.A., Moreira, I.C. and Santos, F.C. (1998) "균질 해밀턴 시스템의 일부 클래스에 대한 Ziglin-Yoshida 분석에 관하여", 브라질 물리학 저널 Vol.28 n.4 상파울루 12월.
- 바레라, 엠마누엘 얀 (2003) 더블 스윙 애트우드의 기계의 역학, B.S. 논문, 필리핀 대학 국립 물리학 연구소.
- Babelon, O, M. Talon, MC Peyranere (2010), "흔들리는 애트우드의 기계에 대한 Kowalevski의 분석", 물리학 저널 A: 수학과 이론 제43권 (8).
- Bruhn, B. (1987) "비선형 발진기의 약하게 결합된 시스템에서의 혼돈과 질서", Physica Scripta Vol.35(1).
- Casasayas, J., N. B. 투필라로, 그리고 A. 누네스(1989) "휘어지는 애트우드 기계의 무한 다양체", 유럽 물리학 저널 Vol.10(10), p173.
- Casasayas, J, A. 누네스, 그리고 N.B. Tufillaro(1990) "스윙 앳우드의 기계: 통합성과 역동성", Journal de Picic Vol.51, p1693.
- 차우더리, A. 로이랑 M. 데브나스(Debnath) (1988) "스윙 앳우드 머신. 원거리 및 근거리 공진 영역", 국제 이론 물리학 저널, Vol. 27(11), p1405-1410.
- 그리피스 D. J. and T. A. 애보트(1992) "놀라운 역학 시연에 대한 논평," 미국 물리학 저널 Vol. 60(10), p951-953.
- Moreira, I.C. and M.A. Almeida (1991) "Nother symmetrys and the Swing Atwood Machine", Journal of Physics II France 1, p711-715.
- 누네스, A., J. 카사야스, N.B. Tufillaro(1995) "일체형 스윙 앳우드 기계의 주기적 궤도," American Journal of Physics Vol.63(2), p121-126.
- Ouazzani-T.H., A. and Ouzzani-Jamil, M. (1995) "Atwood's machine을 스윙하는 일체형 케이스의 Liouville tori의 Biffurcations, Il Nuovo Cimento B Vol. 110 (9).
- Olivier, Pujol, JP Perez, JP Ramis, C. Simo, S. Simon, JA Weil (2010), "Swing Atwood's Machine: 실험 및 수치 결과, 그리고 이론적 연구", Physical D 239, pp. 1067–1081.
- Sears, R. (1995) "놀라운 역학 시연에 대한 논평, American Journal of Physics, Vol. 63(9), p854-855.
- Yehia, H.M., (2006) "기울어진 원뿔 위의 무거운 입자의 운동과 흔들리는 앳우드 기계의 통합성에 관하여", Mechanics Research Communications Vol. 33(5), p711-716.







 라그랑지안 L
라그랑지안 L 























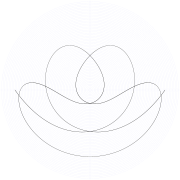












 임의로 커짐에 따라 경계 곡선이 원에 접근합니다. 곡선으로 둘러싸인 지역은 힐스 지역으로 알려져 있습니다.
임의로 커짐에 따라 경계 곡선이 원에 접근합니다. 곡선으로 둘러싸인 지역은 힐스 지역으로 알려져 있습니다.



