로짓 정규 분포

로짓 정규

확률밀도함수
누적분포함수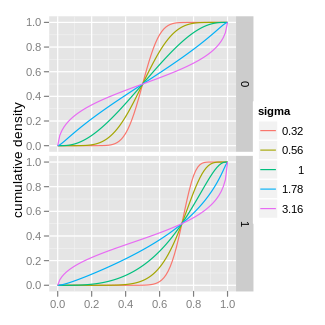
표기법	${\displaystyle P({\mathcal{N})(\mu ,\,\sigma ^{2})}$
매개변수	σ2 > 0 — 제곱 척도(실제), ㎕∈ R — 위치
지원	x ∈ (0, 1)
PDF	${\displaystyle {\frac{1}{\\sqrt{2\pi }}}\,e^{-{\frac {(\fracname {logit}(x)-\mu )^{2}}:{{2}{\frac{1}{x(1-x)}}}}}}}}}}}}}}}}}$
CDF	${\displaystyle {\frac{1}:{1}{{1}:{\Big [}1+\operatorname {erf} {\Big (}{\frac {\operatorname {logit}(x)-\mu }{\sqrt{2\sigma ^}}}{{\Big ]}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$
평균	분석적 해결책 없음
중앙값	$P(\mu )\,}$
모드	분석적 해결책 없음
분산	분석적 해결책 없음
MGF	분석적 해결책 없음

확률론에서 로짓-정규 분포는 로짓이 정규 분포를 갖는 랜덤 변수의 확률 분포다.Y가 정규 분포를 따르는 랜덤 변수이고 P가 표준 로지스틱 함수인 경우 X = P(Y)는 로지트 정규 분포를 가지며, 마찬가지로 X가 로지트(X)= 로그(X/(1-X)가 정규 분포를 따르는 경우 Y = 로지트(X)= 로그(X-X)가 정규 분포를 따른다.로지스틱 정규 분포라고도 하며,^[1] 다항 로짓 버전(예:)^[2][3][4][5]을 가리킨다.null

변수가 0과 1로 경계되고 0과 1의 값이 절대 발생하지 않는 비율인 경우 로짓 정규 분포를 따를 수 있다.null

특성화

확률밀도함수

로짓 정규 분포의 확률밀도함수(PDF)는 0 < x < 1에 대해 다음과 같다.

${\displaystyle f_{X}(x;\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\,{\frac {1}{x(1-x)}}\,e^{-{\frac {(\operatorname {logit} (x)-\mu )^{2}}{2\sigma ^{2}}}}}$

여기서 μ와 μ는 변수 로짓의 평균 및 표준 편차(정의상 변수의 로짓은 정규 분포)이다.null

μ 기호를 변경하여 얻은 밀도는 f(1-x;-μ, μ)와 같다는 점에서 대칭이며, 0.5의 반대쪽(0,1)으로 모드를 이동시킨다.null

순간

로짓 정규 분포의 순간에는 분석 솔루션이 없다.순간은 수치적 통합으로 추정할 수 있지만, $\mu$ ,${}^{}$ , σ ${2\mathrm{}}^{}$ ${\$의 값이 끝점 0과 1에서 무한대로 분산되는 경우$$ 수치적 통합은 엄두도 못 낼 수 있다.다른 방법은 로짓 정규 분포를 정규 랜덤 변수의 변환이라고 하는 관측치를 사용하는 것이다.This allows us to approximate the ${\displaystyle n}$-th moment via the following quasi Monte Carlo estimate ${\displaystyle E[X^{n}]\approx {\frac {1}{K-1}}\sum _{i=1}^{K-1}\left(P\left(\Phi _{\mu ,\sigma ^{2}}^{-1}(i/K)\ri$$ght)\오른쪽)^{n}$

여기서 $P$ ${\$$textstyle$ $P}$은(는) 표준 로지스틱 함수로서 ${\mathrm{\mu }}_{}^{}$,${}_{}^{}$, ${{2\mathrm{}}^{}}_{}^{}$- 1 ${\$$sigma$ $^{2}}^{-1}$은 평균과 분산 $\mu$를 갖는 정규 분포의 역 누적분포함수 입니다$.$^{[clarification needed]}

모드 또는 모드

밀도의 파생물이 0이면 모드 x의 위치는 다음 방정식을 만족한다.

${\displaystyle \logitname {logit}(x)=\filma ^{2}(2x-1)+\mu .}$

매개변수의 일부 값에는 두 가지 해결책이 있다. 즉, 분포는 이원이다.null

다변량 일반화

로지스틱 정규 분포는 다변량 정규 분포의 로지스틱 변환을 통해 D차원 확률 벡터에 대한 로짓-정규 분포의 일반화다.^[6][7][8]null

확률밀도함수

확률밀도함수는 다음과 같다.

${\displaystyle f_{X}(\mathbf {x} ;{\boldsymbol {\mu }},{\boldsymbol {\Sigma }})={\frac {1}{ (2\pi )^{D-1}{\boldsymbol {\Sigma }} ^{\frac {1}{2}}}}\,{\frac {1}{\prod \limits _{i=1}^{D}x_{i}}}\,e^{-{\frac {1}{2}}\left\{\log \left({\frac {\mathbf {x} _{-D}}{x_{D}}}\right)-{\boldsymbol {\mu }}\right\}^{\top }{\boldsymbol {\Sigma }}^{-1}\left\{\log \left({\frac {\mathbf {x} _{-D}{x_{D}}}\오른쪽)-{\boldsymbol{\mu }\\\}\quad \mathbf {x} \in {\mathcal}^{D}\;;,}$

여기서 $x{\displaystyle {\mathbf{}}_{}}$- ${\displaystyle D_{}}$ ${\$은(는$)$ x {\$displaystyle$ \$mathbf {x} }$의 첫 번째(D-1) 성분 벡터를 나타내며, ${\displaystyle S^{}}$ D ${\$는 D차원 확률 벡터의 단순함을 나타낸다$$$$.This follows from applying the additive logistic transformation to map a multivariate normal random variable ${\displaystyle \mathbf {y} \sim {\mathcal {N}}\left({\boldsymbol {\mu }},{\boldsymbol {\Sigma }}\right)\;,\;\mathbf {y} \in \mathbb {R} ^{D-1}}$ to the simplex:

${\displaystyle \mathbf {x} =\left[{\frac {e^{y_{1}}}{1+\sum _{i=1}^{D-1}e^{y_{i}}}},\dots ,{\frac {e^{y_{D-1}}}{1+\sum _{i=1}^{D-1}e^{y_{i}}}},{\frac {1}{1+\sum _{i=1}^{D-1}e^{y_{i}}}}\right]^{\top }}$

고유한 역방향 매핑은 다음을 통해 제공된다.

${\displaystyle \mathbf {y} =\left[\log \left({\frac {x_{1}}{x_{D}}}\right),\dots ,\log \left({\frac {x_{D-1}}{x_{D}}}\right)\right]^{\top }}$.

성분의 합이 1에 이르는 벡터 x의 경우다.s자형 원소가 있는 x의 경우, 즉, 다음과 같은 경우

${\displaystyle \mathbf {y} =\left[\log \left] \left({1-x_{1}:{1-x_{1}}}\right),\log \left({\frac {d}{1-x_{D}}}\rig)^{\\\}}}}}}}:{\}}}}}}}$

우리는 가지고 있다.

${\displaystyle f_{X}(\mathbf {x} ;{\boldsymbol {\mu }},{\boldsymbol {\Sigma }})={\frac {1}{ 2\pi {\boldsymbol {\Sigma }} ^{\frac {1}{2}}}}\,{\frac {1}{\prod \limits _{i=1}^{D}\left(x_{i}(1-x_{i})\right)}}\,e^{-{\frac {1}{2}}\left\{\log \left({\frac {\mathbf {x} }{1-\mathbf {x} }}\right)-{\boldsymbol {\mu }}\right\}^{\top }{\boldsymbol {\Sigma }}^{-1}\\왼쪽\{\log \left\frac {x}{{1-\mathbf {x}}}}}-{\mathbf {x}}-{\mu }\right\}}}}}$

여기서 인수의 로그와 분할은 요소별로 취해진다.변환의 Jacobian 행렬이 요소 $1{\displaystyle \frac{\mathrm{}}{}}$ x ${\displaystyle \frac{i_{}1}{}}$- x ${\displaystyle \frac{i_{}}{}}$) ${\$과(와) 대각선이기 때문이다$.$

통계분석에서 사용

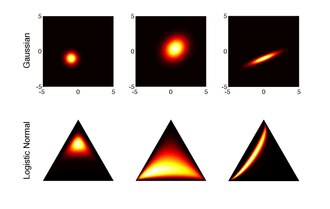
로지스틱 정규 분포는 확률 벡터의 성분들 사이의 상관관계를 포착할 수 있다는 점에서 디리클레 분포에 대한 보다 유연한 대안이다.또한 데이터 벡터 구성요소의 로그 비율에 대한 질문에 대답할 수 있도록 함으로써 구성 데이터의 통계 분석을 단순화할 수 있는 잠재력을 가지고 있다.절대 성분 값보다는 비율에 관심을 갖는 경우가 많다.null

확률 심플렉스(probility simplex)는 경계가 있는 공간으로, $R{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$의 벡터에 일반적으로 적용되는 표준 기법을 덜$$ 의미 있게 만든다.애치슨은 그러한 방법을 단순한 벡터에 직접 적용할 때 거짓 음성 상관관계의 문제를 설명했다.^[7]그러나 적층 로지스틱 변환의 역방향으로$$ $S{\displaystyle {\mathcal{}}^{}}$ ${\displaystyle D^{}}$ ${\$의 합성 데이터를 매핑하면 $R{\displaystyle {\mathbb{}}^{}}$ -${\displaystyle 1^{}}$ ${\$ 이러한 데이터 표현에 표준 기법을 적용할 수 있다.이 접근방식은 로지스틱 정규 분포의 사용을 정당화하므로 "단순함의 가우스"로 간주할 수 있다.null

디리클레 분포와의 관계

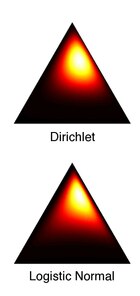
Dirichlet과 로지스틱 정규 분포는 모수의 선택에 있어 결코 정확히 같지 않다.그러나 애치슨은 Kullback-Leibler difference(KL)가 최소화되도록 로지스틱 정규의 디리클레를 근사화하는 방법을 설명했다.

${\displaystyle K(p,q)=\int _{{\mathcal {S}}^{D}}p\left(\mathbf {x} \mid {\boldsymbol {\alpha }}\right)\log \left({\frac {p\left(\mathbf {x} \mid {\boldsymbol {\alpha }}\right)}{q\left(\mathbf {x} \mid {\boldsymbol {\mu }},{\boldsymbol {\Sigma }}\right)}}\right)\,d\mathbf {x} }$

이는 다음을 통해 최소화된다.

${\displaystyle {\boldsymbol {\mu }}^{*}=\mathbf {E} _{p}\left[\log \left({\frac {\mathbf {x} _{-D}}{x_{D}}}\right)\right]\quad ,\quad {\boldsymbol {\Sigma }}^{*}={\textbf {Var}}_{p}\left[\log \left({\frac {\mathbf {x} _{-D}}{x_{D}}}\right)\right]}$

Dirichlet 분포의 모멘트 특성을 사용하여 digamma $\psi {\displaystyle }$ ${\displaystyle \psi}$ 및 trigamma $ma{\displaystyle {}^{}}$ ${\$ 함수의$$ 관점에서 솔루션을 작성할 수 있다.

$\displaystyle \mu _{i}^{*}=\psi \left(\alpha _{i}\right)-\psi \left(\alpha _{D}\right)\quad i=1,\ldots,D-1}$

${\displaystyle \Sigma \sigma _{i}^}=\psi '\좌(\alpha _{i}\우)+\psi '\좌(\alpha _{D}\우)\quad i=1,\ldots,D-1}$

$\displaystyle \Sigma _{ij}^{*}=\psi '\left(\alpha _{D}\right)\quad,\quad i\neq j}$

This approximation is particularly accurate for large ${\displaystyle {\boldsymbol {\alpha }}}$. In fact, one can show that for ${\displaystyle \alpha _{i}\rightarrow \infty ,i=1,\ldots ,D}$, we have that ${\displaystyle p\left(\mathbf {x} \$$미드 {\boldsymbol {\alpha }}\오른쪽)\오른쪽$ 화살표 $q\왼쪽(\mathbf {x}\mid {\\boldsymbol {\\mu }^{*},{\boldsymbol {\}^{*}\오른쪽$

참고 항목

• 베타 분포 및 Kumaraswamy 분포, 유사한 모양의 경계 구간에서의 기타 2-모수 분포

참조

추가 읽기

• Frederic, P. & Lad, F.(2008) 대수 정규 분포의 두 모멘트.통계-시뮬레이션 및 계산에서의 통신.37: 1263-1269
• Mead, R. (1965). "A Generalised Logit-Normal Distribution". Biometrics. 21 (3): 721–732. doi:10.2307/2528553. JSTOR 2528553.

외부 링크

• R용 로지트노멀 패키지