힐버트 변환

수학 및 신호 처리에서 힐버트 변환은 실제 변수의 u(t) 함수를 취하고 실제 변수 H(u)(t)의 다른 함수를 생성하는 특정 선형 연산자다. 이 선형 연산자는 $함수{\displaystyle \mathrm{}}$ 1${\displaystyle }$/ (${\displaystyle \pi }$ ${\displaystyle t}$) ${\displaystyle$ 1$/(\pi t)}$을(를) 가진 콘볼루션에 의해 주어진다(§ Definition 참조). 힐버트 변환은 주파수 영역에서 특히 단순한 표현을 가지고 있다. ±90°의 위상 편차를 전달한다().½ 라디안)은 함수의 모든 주파수 성분에 대한 것으로, 주파수 부호에 따른 이동의 부호(§ 푸리에 변환과의 관계 참조). 힐버트 변환은 신호 처리에서 중요한데, 여기서 힐버트 변환은 실제값 신호 u(t)의 분석적 표현의 구성요소다. 힐버트 변환은 분석 기능에 대한 리만-힐버트 문제의 특수한 사례를 해결하기 위해 데이비드 힐버트가 이 설정에서 처음 도입했다.

정의

u의 힐베르트 변환의 u(t)의 기능 h(t)).mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{과 주름으로 생각될 수 있다.디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/π지 마, 그 코시 커널로 알려져 있다. ½t는 t = 0에 걸쳐 통합할 수 없기 때문에, 콘볼루션을 정의하는 적분은 항상 수렴하지 않는다. 대신에 힐버트 변환은 Cauchy principal value(여기서 p.v.로 표시됨)를 사용하여 정의된다. 명시적으로 힐버트 변환은 함수(또는 신호) u(t)에 의해 주어진다.

이 적분이 주된 값으로 존재한다면. 이것은 정확히 강화 분포 p.v. 1/4 t와 u의 경합이다.^[1] 또는 변수를 변경함으로써 다음과 같이 주 값 적분을 명시적으로^[2] 작성할 수 있다.

힐버트 변환을 함수 u에 연속해서 두 번 적용하면 결과는 마이너스 u:

두 반복을 정의하는 통합이 적절한 의미로 수렴될 경우. 특히 역변형은 -H이다. 이러한 사실은 힐버트 변환이 u(t)의 푸리에 변환에 미치는 영향을 고려함으로써 가장 쉽게 알 수 있다(아래 § Relationship with the Fourier 변환 참조).

상부 하프 평면의 분석 함수의 경우, 힐버트 변환은 경계 값의 실제 부분과 가상 부분 사이의 관계를 설명한다. 즉, 이 힐버트 변환이 존재한다면, 상반복구 평면 {z : Im{z} > 0}, u(t) = Re{f(t + 0·i)}, 임{f(t + 0·i) = H(u)(t)까지 분석한다.

표기법

신호 처리에서 u(${\displaystyle t}$)의 힐버트 변환은 일반적으로 $u{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$( t${\displaystyle }$) ${\displaystyle {\hat{u}}(t)}$에 의해 표시되지만, 수학에서는 이미 이 표기법이 u(t)의 푸리에 변환을 나타내는 데 광범위하게 사용되고 있다.^[3][4] 때때로 힐버트 변환은 $u{\displaystyle \stackrel{}{}}$~${\displaystyle }$( ${\displaystyle t}$) ${\displaystyle {\tilde{\}}(t)}$에 의해 표시되기도 한다$.$ 더욱이 많은 출처에서는 힐버트 변환을 여기서 정의한 변환의 음으로 정의한다.^[5]

역사

힐버트 변환은 리만이 제기한 분석 기능에 관한 문제에 관한 1905년 힐버트의 연구에서 발생했는데,[6]^[7] 리만-힐버트 문제로 알려지게 되었다. 힐버트의 작업은 주로 원에 정의된 기능에 대한 힐버트 변환과 관련이 있었다.^[8][9] 이산 힐버트 트랜스포메이션과 관련된 그의 초기 작품 중 일부는 괴팅겐에서 행한 강연으로 거슬러 올라간다. 그 결과는 후에 헤르만 바일이 논문에서 발표하였다.^[10] 슈르는 별개의 힐버트 변환에 대한 힐버트의 결과를 개선하여 통합 케이스로 확장시켰다.^[11] 이러한 결과는 L과² ℓ² 공간으로 제한되었다. 1928년에, 마르셀 리스는 힐베르트 변환 너의 p({\displaystyle L^{p}(\mathbb{R})}(Lp공간)에서 1<>에 대해 정의할 수 있다; 와<>∞, Lp({\displaystyle L^{p}(\mathbb{R})에 1<>는 힐베르트 변환은 한정적 연산자}; 와<>∞, 그리고가 비슷한 결과는 힐베르트가 가지고 있다는 것을 증명했다.변환 제일의 것이다원과 분리된 힐버트 변환.^[12] 힐버트 변환은 안토니 지그문트와 알베르토 칼데론에게 단일한 통합에 대한 연구를 하는 동안 동기부여가 되는 예였다.^[13] 그들의 조사는 현대 조화 분석에 근본적인 역할을 했다. 힐버트 변환의 다양한 일반화들, 예를 들어 이선형 및 삼선형 힐버트 변환은 오늘날에도 여전히 연구의 활발한 분야들이다.

푸리에 변환과의 관계

힐버트 변환은 멀티플라이어 연산자다.^[14] H의 승수는 σ_H(Ω) = -i sgn(Ω)이며 여기서 sgn은 기호함수다. 따라서 다음과 같다.

여기서 $F{\displaystyle \mathcal{}}$ ${\$은(는) 푸리에 변환을 의미한다$$. sgn(x) = sgn(2πx)이기 때문에 이 결과는 $F{\displaystyle \mathcal{}}$ ${\${\$mathcal {F}$의 세 가지 공통 정의에 적용된다$.$

오일러의 공식에 따르면

따라서 H(u)(t)는 u(t)의 음주파수 성분의 위상이 +90°(½ 라디안), 양주파수 성분의 위상이 -90°만큼 이동하는 효과가 있으며, i·H(u)(t)는 음주파수 성분의 위상이 +90° 더 이동하면서 양주파수 성분을 복원하는 효과가 있어 부정이 발생한다. (즉, 곱하기 by -1)

힐버트 변환을 두 번 적용하면 u(t)의 음과 양의 주파수 성분의 위상이 각각 +180°, -180° 등량만큼 이동한다. 신호는 부정된다. 즉, H(H(u) = -u.

선택한 Hilbert 변환 표

다음 표에서는 주파수 파라미터 $\Omega {\displaystyle }$ ${\displaystyle \omega }$이(가) 실재한다$$.

신호 ${\displaystyle u(t)}$	힐버트 변환[fn 1] ${\displaystyle \operatorname {H}(u)(t)}$
$\displaystyle \sin(\omega t)}$ [fn 2]	${\displaystyle {\lll}\sin \left(\omega t-{\tfrac {}{pi }{2}}\right),\migration \omega >0\\\\\sin(\omega t+{\pi }{2}}\rig})\ndata.$
$\displaystyle \cos(\omega t)}$ [fn 2]	${\displaystyle {\lll}{lll}\cos \left(\omega t-{\tfrac {}{pi }{2}}\right),\cos \reft(\omega t+{\pi }{2}}\right)\cos \ega <0\end}}}}}$
${\displaystyle e^{i\omega t}}$	${\displaystyle {\pi{now}{lll}e^{i\왼쪽(\omega t-{\tfrac {}{2}}\오른쪽),\mige \omega >0\e^(\omega t+{\pi{2}}\오른쪽)},\migomega <0\end{array}}}}}}$
${\displaystyle e^{-i\omega t}$	${\displaystyle {\cHB{now}{lll}e^{-i\left(\omega t-{\tfrac {}{2}}\오른쪽),\migration \omega >0\e^(\omega t+{\tfrac {}{2}}\오른쪽)},\migmergie <0}$
${\displaystyle 1 \over t^{2}+1}$	${\displaystyle t \over t^{2}+1}$
${\displaystyle e^{-t^{2}}$	${\displaystyle {\frac {2}{\\sqrt {\pi \,}F(t)}$ (Dawson 함수 참조)
동기 함수 $\displaystyle \sin(t) \over t}$	$\displaystyle 1-\cos(t) \over t}$
디라크 델타 함수 $[\displaystyle \cHB(t)}$	${\displaystyle {1\over \pi t}}$
특성 함수 ${\displaystyle \chi _{[a,b]}(t)}$	${\displaystyle {{\frac{1}{\,\pi \}\ln \left\vert {\frac {t-a}{t-b}\right\vert }}}$

메모들

힐버트 변환의 광범위한 표를 구할 수 있다.^[15] 힐버트 변환 상수는 0이라는 점에 유의하십시오.

정의의 영역

힐버트 변환이 제대로 정의되어 있다는 것은 결코 명백하지 않다. 그것을 정의하는 부적절한 적분은 적절한 의미로 수렴되어야 하기 때문이다. 그러나 힐버트 변환은 넓은 종류의 ${\displaystyle {함수}^{}}$, 즉 1 p < ∞에 대해$$ L $p{\displaystyle {}^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle L^{p}(\mathb$ {$R}$)에 있는 함수들에 대해 잘 정의되어 있다.

보다 정확히 말하면, 1< p < ∞>에 대해$$ u가 L $p{\displaystyle {}^{}}$( ${\displaystyle R^{}}$) ${\displaystyle$ L$^{p}(\mathb {R} )}$에 있는 경우, 부적절한 적분을 정의하는 한계.

거의 모든 t에 존재한다. 한계함수는 또한 $L{\displaystyle {}^{}}$ ${\displaystyle p^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle$ L$^{p}(\mathb {R}$)에 있으며, 사실$$ 부적절한 적분 평균의 한계이기도 하다. 그것은

Titchmarsh 정리(Titchmarsh 정리)에 의해 거의 모든 곳에서 포인트로 ε → L^p 규범에 0으로 표시된다.^[16]

사례 p = 1의 경우, 힐버트 변환은 여전히 거의 모든 곳에서 포인트로 수렴되지만, 그 자체는 지역적으로 통합되지 못할 수도 있다.^[17] 특히 평균의 수렴은 일반적으로 이 경우 발생하지 않는다. 그러나¹ L 함수의 힐버트 변환은 L-weak에서¹ 수렴하며, Hilbert 변환은 L에서¹ L까지의^1,w 경계 연산자(^[18]특히 Hilbert 변환은 L², Marcinkiewicz 보간법의 승수 연산자이기도 하고 이중성 주장은 H가 L에^p 경계한다는 대체 증거를 제공하므로)이다.

특성.

경계성

${\displaystyle 1^{}}$ < p < ∞, L $p{\displaystyle {}^{}}$ (${\displaystyle {}^{}R\mathbb{}}$) ${\displaystyle$ L$^{p}(\mathb {R})}$에 대한 힐버트 변환이 경계 선형 연산자라면 다음과 같은 상수 C가_p 존재한다는 뜻이다.

모든 $u{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle {}^{}}$ ${\displaystyle p\mathbb{}{}^{}}$( R${\displaystyle }$) ${\displaystyle u\in L^{p}(\mathb {R} )}$에 대해$.$^[19]

최상의 상수 $C{\displaystyle {}_{}}$ ${\displaystyle p_{}}$ ${\$은(는) 다음에^[20] 의해 주어진다$$.

An easy way to find the best ${\displaystyle C_{p}}$ for ${\displaystyle p}$ being a power of 2 is through the so-called Cotlar's identity that ${\displaystyle (\operatorname {H} f)^{2}=f^{2}+2\operatorname {H} (f\operatorname {H} f)}$ for all real valued f. 주기적인 힐버트 변환에 대해 동일한 최상의 상수가 유지된다.

Hilbert 변환의 한계성은 대칭 부분 합계 연산자의 ${\displaystyle L^{}}$ p${\displaystyle {}^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle$ L$^{p}(\mathb$ {$R}$ )$$정합성을$$ 의미한다.

to f in $L{\displaystyle {}^{}}$ ${\displaystyle p^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle$ L$^{p}(\mathb {R}$ $)\}.$^[21]

반자위주의

The Hilbert transform is an anti-self adjoint operator relative to the duality pairing between ${\displaystyle L^{p}(\mathbb {R} )}$ and the dual space ${\displaystyle L^{q}(\mathbb {R} )}$, where p and q are Hölder conjugates and 1 < p, q < ∞. Symbolically,

$u{\displaystyle }$∈ ${\displaystyle {}^{}}$ ${\displaystyle p^{}}$( R${\displaystyle }$) ${\displaystyle u\in$ L$^{p}(\mathb {R})}$ 및 $v$ ${\displaystyle \in }$ ${\displaystyle {Lq}^{}}$(${\displaystyle R\mathbb{}}$) ${\displaystyle v\in L^{q}(\mathb {R} )}$용$.$^[22]

역변환

힐베르트 변환은 반투과인데,^[23] 그 의미는 다음과 같다.

각 변환이 잘 정의되어 있는 경우. H는 공간 $L{\displaystyle {}^{}}$ ${\displaystyle p^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle L^{p}(\mathb {R} )$를 보존하므로$,$ 이는 특히 힐버트 변환이 L ${\displaystyle p^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle L^{p}(\mathb {R}$)에서 변환할 수 없다는 것을 의미한다$.$

복합구조

${\displaystyle H^{}}$² = -I("I"는 L p${\displaystyle {}^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle L^{p}(\mathb {R} )}$의 실제 바나흐 공간에 대한 Hilbert 변환은 이 바나흐 공간에 선형 복합 구조를 정의한다$.$ 특히 p = 2일 때 힐버트 변환은 복잡한 힐버트 공간의 구조로$$ L ${\displaystyle {2\mathrm{}}^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle L^{2}(\mathb {R} )}$에 실제 가치 함수의 힐버트 공간을 제공한다.

힐버트 변환의 (복잡한) 고유상태는 Paley-Wiener 정리에 의한 하디 공간 H의² 상·하반 평면에서의 홀로모르픽 함수로서 표현을 인정한다.

차별화

공식적으로 힐버트 변환의 파생상품은 파생상품의 힐버트 변환이다. 즉, 이 두 선형 연산자가 통근한다.

이 정체성을 반복해서

이는 u에 명시된 바와 같이 엄밀하게 사실이며, 첫 번째 k 파생상품은 L ${\displaystyle p^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle L^{p}(\mathb {R} )}$에 속하며$,$^[24] 분화가 Ω으로 곱해지는 주파수 영역에서 쉽게 확인할 수 있다.

컨버설

힐버트 변환은 강화분포를^[25] 통한 콘볼루션으로서 공식적으로 실현될 수 있다.

그래서 공식적으로,

단, 선행은 콤팩트 서포트의 배포에 대해서만 정의될 수 있다. 조밀하게 지원되는 기능(포티오리 분포)은^p L에 밀도가 높기 때문에 이를 통해 다소 엄격하게 작업할 수 있다. 또는 h(t)가 함수 로그 t/t의 분포적 파생상품이라는 사실을 wit에 사용할 수 있다.

대부분의 운영 목적에서 힐버트 변환은 콘볼루션으로 취급될 수 있다. 예를 들어, 형식적인 의미에서, 힐버트 변환은 다음 두 가지 요소 중 하나에만 적용되는 힐버트 변환의 콘볼루션이다.

이는 만약 u와 v가 그 경우에, 그 이후, 압축적으로 지원되는 분배라면 엄밀하게 사실이다.

따라서 적절한 한계에 도달함으로써, u l L과^p v l L이^q 다음을 제공한 경우에도 마찬가지다.

티치마르슈로 인한 정리로부터.^[26]

인비언스

Hilbert 변환은 L ${\displaystyle {2\mathrm{}}^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle$ L$^{2}(\mathb {R} )}$에 다음과 같은 invariance 속성을 가지고 있다$.$

• 그것은 번역으로 통용된다. 즉$,$ $모든{\displaystyle \mathbb{}}$ a in_a R. {\$displaystyle \mathb$ {$R}$에 대해 연산자 T f($x)$ = f(x + a)와 통근한다.
• 그것은 양의 팽창으로 통한다. 즉, 연산자 M_λ f (x) = f (f) 는 모든 λ > 0에 대해 통근한다.
• 반사 R f(x) = f(-x)로 반공칭한다.

승수 상수까지 Hilbert 변환은 이러한² 특성을 가진 L에서 유일한 경계 연산자다.^[27]

사실 힐버트 변환과 함께 통근하는 더 광범위한 운영자들이 있다. ${\displaystyle 그룹\mathbb{}}$ ${\displaystyle \text{SL}(2}$, R${\displaystyle }$) ${\displaystyle {\text{$$SL}(2,\mathb {R})$은 공식으로$$ ${\displaystyle {L\mathrm{}}^{}}$ $2{\displaystyle {}^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle L^{2}(\mathb {R} )}$ 공간에 대해 단일 연산자 U에_g 의해 작용한다$$.

이 단일 표현은 ${\displaystyle SL\mathbb{}}$ (${\displaystyle 2,}$R${\displaystyle }$)${\displaystyle }$. ${\디스플레이$ 스타일 $~{\text{{\$text}의 주계열 표현 예다.$SL2}}(2,\mathb {R} )~.}$ 이 경우$$ 환원 가능하며, 두 개의 불변 서브스페이스인 $Hardy{\displaystyle {}^{}}$ space H ${\displaystyle {2\mathrm{}}^{}}$(${\displaystyle R\mathbb{}}$ ){\$displaystyle H^{2}(\mathb$ {R}$)$와 그 결합으로 분할된다. 상·하부 반평면에 있는 홀로모르픽 함수의² L 경계값의 공간이다. ${\displaystyle H^{}}$ ${\displaystyle {2\mathrm{}}^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle H^{2}(\mathb {R} )}$과(와)의 결합은 각각 실제 축의 음과 양 부분에 소멸되는 푸리에 변환을 가진² L 함수로 구성된다. Since the Hilbert transform is equal to H = −i (2P − I), with P being the orthogonal projection from ${\displaystyle L^{2}(\mathbb {R} )}$ onto ${\displaystyle \operatorname {H} ^{2}(\mathbb {R} ),}$ and I the identity operator, it follows that ${\displaystyle \operatorname {H}$$^{2}(\mathb {R}$ )$$및$$ 그 직교는 고유값 ±i에 대한 H의 Eigenspaces이다. 즉, H는 연산자_g U와 통근한다. 연산자 U_g ~ $H{\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle (R\mathbb{}}$) ${\displaystyle \operatorname {H} ^{2}(\mathb {R}$) 및 그$$ 결합은 ${\displaystyle \text{SL}}$( ${\displaystyle 2}$, ${\displaystyle R\mathbb{}}$) ${\displaystyle {\text}$을(으)로 해석할 수 없는 표현을 제공한다.$SL}(2,\mathb {R}$ )$$– 소위 이산형 영상 시리즈 표현 한계.^[28]

정의 도메인 확장

Hilbert 분포 변환

힐버트 변환을 특정 분포 공간까지 확장할 수 있다(Pandey 1996, 3장). Hilbert 변환은 분화에 따라 통용되고 L의^p 경계 연산자이기 때문에 H는 Sobollev 공간의 역한계에 대해 연속적인 변환을 제공하도록 제한한다.

그런 다음 힐버트 변환은 L^p 분포로 구성된 $D{\displaystyle {\mathcal{}}_{}^{}}$ ${\displaystyle {L^{}}_{}^{}}$ ${\displaystyle {\$$d}_$${L^{p}}$의 이중 공간에서 정의할 수 있다$.$ 이는 이중성 쌍을 통해 달성된다.
$u{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle {\mathcal{}}_{}^{}}$ ${\displaystyle L_{{}^{}}^{}}$ ${\displaystyle {p^{}}_{}^{}}$ ${\displaystyle {{}^{}}_{}^{}}$ ${\$에 대해 다음을 정의하십시오$.$

겔판드와 실로프 때문에 접근에 의해서도 강화 분배의 공간에 대한 힐버트 변환을 정의할 수 있지만,^[29] 적분에서의 특이성 때문에 상당히 더 많은 주의가 필요하다.

경계함수의 힐버트 변환

Hilbert 변환은 $L{\displaystyle {}^{}}$ ${\displaystyle {\infty \mathrm{}}^{}}$( $){\displaystyle L^{\infit }(\mathb {R}$)의$$ 기능에 대해서도 정의할 수 있지만, 약간의 수정과 주의사항이 필요하다. 적절하게 이해한 힐버트 변환 맵 $L{\displaystyle {}^{}}$ ${\displaystyle {\infty \mathrm{}}^{}}$( R${\displaystyle }$) ${\displaystyle$ L$^{\infit }(\mathb {R}$)은 경계 평균 진동(BMO) 클래스의 Banach 공간에 대한 것이다$$.

순진하게 해석하면 경계 함수의 힐버트 변환은 분명히 잘못 정의되어 있다. 예를 들어, u = sgn(x)을 사용하면, 적분 정의 H(u)는 거의 모든 곳에서 ±3으로 분산된다. 따라서 이러한^∞ 어려움을 완화하기 위해 L 함수의 힐버트 변환은 다음과 같은 정규화된 형태의 적분으로 정의된다.

여기서, 위 h(x) = 1/2x 및

수정된 변환 H는 칼데론과 자이그문트의 일반적인 결과로부터 콤팩트 서포트 기능에 관한 원래의 변환에 동의한다.^[30] 더욱이, 그 결과로 생기는 적분은 BMO 규범과 관련하여 거의 모든 곳에서 점방향으로 경계 평균 진동 함수로 수렴된다.

Fefferman의 연구의^[31] 깊은 결과는 함수가 $일부{\displaystyle }$ f${\displaystyle }$, ${\displaystyle g}$ ${\displaystyle \in }$ ${\displaystyle {}^{}}$ ${\displaystyle {\infty \mathrm{}}^{}}$( R${\displaystyle }$) ${\displaystyle f,g\in l^{\infort }(\mathb {R} )}$에 대해 f + H(${\displaystyle g\mathbb{}}$) 형식을 가진 경우에만 경계 평균 진동이라는 것이다$.$

결합 함수

힐버트 변환은 함수 f(x)와 g(x)의 쌍으로 이해할 수 있다.

상부 하프 평면에 있는 홀로모르픽 함수 F(z)의 경계 값이다.^[32] 이런 상황에서 f와 g가 충분히 통합이 가능하다면 하나는 다른 하나의 힐버트 변환이다.

$f{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle {}^{}}$ ${\displaystyle p^{}}$( ${\displaystyle R\mathbb{}}$)${\displaystyle }$. ${\displaystyle f\in L^{p}(\mathb {R} )}$ 그렇다면$$ 포아송 적분 이론에 의해 f는 상부 하프 평면으로의 고유한 고조파 확장을 인정하고, 이 확장은 다음과 같이 주어진다.

포아송 커널과 f의 콘볼루션인

더욱이 상반면에 F(z) = u(z) + i v(z)가 홀로모르픽이고

이 조화 함수는 f로부터 공극 포아송 커널로 콘볼루션을 취함으로써 얻어진다.

그러므로

실제로 카우치 알맹이의 실제와 상상의 부분은

그래서 F = u + i v는 Cauchy의 적분 공식에 의해 홀로모르픽이 된다.

이런 식으로 u로부터 얻은 함수 v를 u의 조화결합이라고 한다. y → 0으로 v(x,y)의 (비 접선) 경계 한계는 f의 힐버트 변환이다. 그래서 간결하게

티치마르슈 정리

티치마르슈의 정리(E. C를 위해 명명) 1937년 자신의 작품에 그것을 포함시킨 티치마르슈)는 상부 하프 평면에서 홀로모르프 함수의 경계 값과 힐버트 변환 사이의 관계를 정밀하게 만든다.^[33] 그것은 실제 라인의 복합 값 제곱-적분함수 F(x)가 상부 반평면 U의 홀로모르픽 함수의 하디 공간 H²(U) 내 함수의 경계값이 되도록 필요하고도 충분한 조건을 제공한다.

정리는 복합 값 제곱합성함수 $F{\displaystyle }$: ${\displaystyle R\mathbb{}}$→ ${\displaystyle C\mathbb{}}$ ${\$ F$:\mathb {R} \to \mathb {C}$\to \mathb {C}}에 대한 다음과 같은 조건이 동등하다고$$ 기술하고 있다.

• F(x)는 다음과 같은 방법으로 상부 하프 평면에서 홀로모르픽 함수 F(z)의 z → x로 제한된다.
  $${\daystyle \int _{-\infit _{-\infit }F(x+i\,y) ^{2}\;\mathrm {d}x<K}$$

  
• F(x)의 실제와 상상의 부분은 서로의 힐버트 변형이다.
• 푸리에 변환 $F{\displaystyle \mathcal{}}$( ${\displaystyle F}$)${\displaystyle }$( x${\displaystyle }$) ${\displaystyle {\mathcal {F}(F)}(x)}$은(는) x < 0에 대해$$ 사라진다.

p > 1. 등급 L의 기능에 대해서는^p 약한 결과가 참이다.^[34] 구체적으로는 F(z)가 다음과 같은 홀로모르픽 함수인 경우

모든 y에 대해, $L{\displaystyle {}^{}{p}^{}}$ (${\displaystyle R\mathbb{}}$ )$${\$displaystyle$ L$^{p}(\mathb {R} )}$에 y → 0(대부분의 홀딩 포인트뿐만 아니라)으로^p F(x + i y) → F(x)가 L 규범에 있는 복합$$ 값 함수 F(x)가 있다. 더 나아가

여기서 f는 L ${\displaystyle p^{}}$( ${\displaystyle R\mathbb{}}$) ${\displaystyle L^{p}(\mathb {R}$)의 실제 값 함수이고 g는 f의 Hilbert 변환(클래스^p L)이다$$.

사례 p = 1에서는 그렇지 않다. 사실, L¹ 함수의 힐버트 변환은 다른 L¹ 함수에 평균으로 수렴할 필요가 없다. 그럼에도 불구하고 ^[35]f의 힐버트 변환은 거의 모든 곳에서 다음과 같은 유한 함수 g로 수렴한다.

이 결과는 안드레이 콜모고로프가 디스크에서 하디 기능을 하는 것과 직접적으로 유사하다.^[36] 보통 티치마르슈의 정리라고 불리지만, 그 결과는 리츠, 힐, 타마르킨의^[37] 작품뿐만 아니라 하디, 팰리, 위너(페일리-위너 정리 참조)를 포함한 다른 사람들의 많은 작품들을 집대성한 것이다.

리만-힐버트 문제

Riemann-Hilbert 문제의₊ 한 형태는 F가 상부 하프 평면에서 홀모픽이고 F는₋ 하부 하프 평면에서 홀모픽이며, F는 실제 축을 따라 x에 대해 홀모픽이 되는 기능 F와₊ F의₋ 쌍을 식별하고자 한다.

여기서 f(x)는 $x{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle R\mathbb{}}$ ${\$의 주어진 실제 값 함수다$.$ 이 방정식의 왼쪽은 F의_± 한계와 적절한 반평형 사이의 차이 또는 과기능 분포로 이해할 수 있다. 이 형태의 두 가지 기능은 리만-힐버트 문제의 해결책이다.

형식적으로 F가_± 리만-힐버트 문제를 풀면

그 다음 f(x)의 힐버트 변환은 에 의해^[38] 주어진다.

힐베르트의 원형 변형

주기적 함수 f에 대해 순환 Hilbert 변환은 다음과 같이 정의된다.

원형 힐버트 변환은 하디 공간의 특성을 부여하고 푸리에 시리즈의 콘게이트 기능을 연구하는 데 사용된다. 알맹이,

힐버트 커널은 원래 이런 형태로 연구되었기 때문에 힐버트 커널로 알려져 있다.^[8]

힐버트 커널(순환 힐버트 변환용)은 카우치 커널을 ½x 주기적으로 만들어 얻을 수 있다. 보다 정확하게, x ≠ 0의 경우

순환 힐버트 변환에 대한 많은 결과는 이 대응관계에서 힐버트 변환에 대한 해당 결과로부터 도출될 수 있다.

또 다른 직접적인 연결은 Cayley transform C(x) = (x – i) / (x + i)에 의해 제공되며, 이 변환은 실제 선을 원에, 상반면은 유닛 디스크에 전달한다. 그것은 단일 지도를 유도한다.

$L$² ${\displaystyle {2\mathrm{}}^{}}$( ${\displaystyle R\mathbb{}}$)$$. {\$displaystyle$ L$^{2}(\mathb$ {$R}$)$$$}$ 연산자 ${\displaystyle U}$는 Hardy 공간 H 2 ( R ) {\$displaystyle H^{2}(\mathb {R}$^[39]$)$에 Hardy 공간 H${\displaystyle {}^{}}$T²)를 운반한다.

신호 처리에서 Hilbert 변환

베드로시안 정리

베드로시안 정리에서는 비과첩 스펙트럼을 가진 로우패스 및 하이패스 신호의 생산물의 힐버트 변환은 하이패스 신호의 생산물 및 힐버트 변환물 또는 하이패스 신호의 생산물에 의해 주어진다.

여기서 f와_LP f는_HP 각각 로우패스 신호와 하이패스 신호다.^[40] 이것이 적용되는 통신 신호의 범주를 협대역 신호 모델이라고 한다. 이 범주의 멤버는 고주파 사인파 "캐리어"의 진폭 변조다.

여기서 u_m(t)는 음성 또는 음악과 같은 좁은 대역폭 "초음파" 파형이다. 그리고 베드로이센의 정리로는 다음과 같다.^[41]

분석적 표현

특정 유형의 결합 함수는 다음과 같다.

$u{\displaystyle }$( ${\displaystyle t}$)${\displaystyle }$. ${\displaystyle u(t$)의 분석적 표현으로 알려져 있다$.$$}}$ 이 이름은 주로 오일러의 공식에 기인하는 수학적 추적성을 반영한다$$. 협대역 모델에 베드로이센의 정리를 적용하면,^[42] 분석적 표현은 다음과 같다.

푸리에 변환 속성은 이 복잡한 헤테로디네 연산이 u_m(t)의 모든 음의 주파수 성분을 0Hz 이상으로 이동할 수 있음을 나타낸다. 그 경우 결과의 상상적인 부분은 실제 부분의 힐버트 변형이다. 이것은 힐버트 변환을 만드는 간접적인 방법이다.

각도(위상/주파수) 변조

양식:^[43]

위상 변조 및 주파수 변조를 모두 포함하는 각도 변조라고 한다. 순간 주파수는 Ω${\displaystyle }$+ ${\displaystyle \mathrm{\varphi m}}$ ${\displaystyle {}_{}^{}}$( t${\displaystyle }$)${\displaystyle }$. ${\displaystyle \omega +\phi _{m}^{\prime$ }($t)$이다$.$$}}$ $\Omega {\displaystyle {}_{}^{}}$ 충분히 큰 경우$$, compared ${\displaystyle m_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\$ $\}\}\}$ :

및:

단일 사이드밴드 변조(SSB)

Eq.1의 u_m(t)도 (메시지 파형의 분석적 표현)일 경우, 즉 다음과 같다.

단측대역 변조 결과:

전송된 구성 요소의 경우:^[44][45]

인과성

$함수{\displaystyle }$ h${\displaystyle (}$ ${\displaystyle t}$)${\displaystyle }$= ${\displaystyle 1}$/ (${\displaystyle \pi }$ t${\displaystyle }$) ${\displaystyle h(t)=1/(\pi t)}$은 콘볼루션으로서 실제 구현에 대한 두 가지 과제를 제시한다$$.

• 그 기간은 무한하다(기술적으로 무한 지원). 대신 유한 길이 근사치를 사용해야 한다. 그러나 길이를 윈도우로 설정하면 변환의 유효 주파수 범위도 감소한다. 창문이 짧을수록 저주파 및 고주파에서 손실이 크다. 4차 필터를 참조하십시오.
• 그것은 비침습 필터다. 따라서 지연 버전 $h{\displaystyle (t}$ -${\displaystyle \tau }$)${\displaystyle }$, ${\$디스플레이 $스타일 h(t-\tau ),}$이(가) 필요하다$$. 이후 해당 출력이 $\tau {\displaystyle .}$ ${\displaystyle \tau .}$해석 신호의 가상 부분을$$ 생성할 때는 소스(실제 부분)를 동등한 양만큼 지연시켜야 한다.

이산 힐버트 변환

For a discrete function, ${\displaystyle u[n]}$, with discrete-time Fourier transform (DTFT), ${\displaystyle U(\omega )}$, and discrete Hilbert transform ${\displaystyle {\hat {u}}[n]}$, the DTFT of ${\displaystyle {\hat {u}}[n]}$ in the region −π < ω < π is given by:

역 DTFT는 콘볼루션 정리를 사용하여 다음과 같다.^[46]

어디에

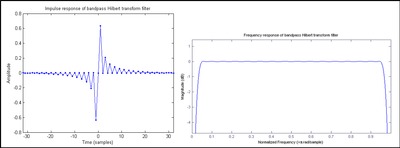
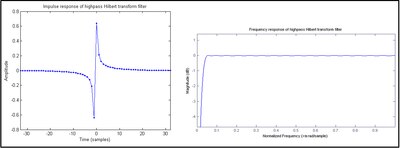
무한충동반응(IIIR)이다. 경련이 수치적으로 수행되면 그림 1과 같이 FIR 근사치가 h[n]로 대체된다. 홀수 수의 대칭 계수가 있는 FIR 필터를 타입 III라고 하는데, 이 필터는 본질적으로 주파수 0과 나이키스트에서 0의 크기 반응을 나타내며, 밴드패스 필터 형태로 이러한 경우를 초래한다. IV형 설계(반대칭 계수의 짝수)는 그림 2에 나타나 있다. 나이키스트 주파수의 크기 반응은 떨어지지 않기 때문에 홀수탭 필터보다 약간 나은 이상적인 힐버트 변압기에 가깝다. 그러나

• 일반적인 (즉, 적절히 필터링되고 샘플링된) u[n] 시퀀스는 나이키스트 주파수에서 유용한 구성요소가 없다.
• Type IV 임펄스 응답은 h[n] 시퀀스에서 1/2 샘플 시프트를 필요로 한다. 이는 그림 2와 같이 0이 아닌 계수를 0이 되게 한다. 따라서 타입 III 설계는 잠재적으로 타입 IV보다 2배 더 효율적이다.
• 타입 III 설계의 그룹 지연은 ^ [ n ${\displaystyle {\u}[n]}$을(를) ${\displaystyle u}$[n${\displaystyle ]}$ ,$${\$displaystyle u$[n$]}$과(${\displaystyle 와}$) 정렬하여 분석 신호를 생성하기 용이하다. 타입 IV의 그룹 지연은 두 표본의 중간이다.

MATLAB 함수, 힐버트(u,N)^[47]는 u[n] 시퀀스와 주기적인 합계를 결합한다.^[A]

${\displaystyle h_{N}[n]\ \triangleq \sum _{m=-\infit }^{\infit }h[n-mN]}}$ ^[B][C]

그리고 복잡한 값 출력 시퀀스의 가상 부분에 주기적 결과의 1주기(N 샘플)를 반환한다. 콘볼루션은 -i sgn(Ω) 분포의 샘플(실제 성분과 가상 성분은 모두 0 또는 ±1에 불과함)과$$ 함께 어레이 D ${\displaystyle \mathrm{F}}$ T${\displaystyle (u}$[$]$ ) ${\${\$dmathrm {DFT}}\preft($왼쪽[$n]\right)$의 곱으로 주파수 영역에서 구현된다. 그림 3은 h_N[n]의 하프 사이클과 h[n]의 등가 길이 부분을 비교한다. Given an FIR approximation for ${\displaystyle h[n],}$ denoted by ${\displaystyle {\tilde {h}}[n],}$ substituting ${\displaystyle {\scriptstyle \mathrm {DFT} }\left({\tilde {h}}[n]\right)}$ for the −i sgn(ω) samples results in an FIR version of the convolution.

출력 시퀀스의 실제 부분은 원래 입력 시퀀스여서 복잡한 출력은 u[n]의 분석적 표현이다. 입력이 순수한 코사인의 한 부분인 경우, N의 두 가지 다른 값에 대한 결과적 경련이 그림 4(빨간색 및 청색 그림)에 묘사되어 있다. 에지 효과는 결과가 순수한 사인 함수(녹색 그림)가 되는 것을 방지한다. h_N[n]은 FIR 시퀀스가 아니기 때문에 효과의 이론적 범위는 전체 출력 시퀀스다. 그러나 사인 함수와의 차이는 가장자리로부터의 거리에 따라 감소한다. 파라미터 N은 출력 시퀀스 길이 입니다. 입력 시퀀스의 길이를 초과할 경우 0 값 요소를 추가하여 입력을 수정한다. 대부분의 경우, 그것은 차이의 크기를 감소시킨다. 그러나 그들의 지속시간은 h[n]충동반응의 고유한 상승과 하강시간에 의해 지배된다.

u[n] 시퀀스의 긴 convolution을 수행하기 위해 overlap-save라고 불리는 방법을 사용할 때 가장자리 효과에 대한 감상이 중요하다. 길이 N의 세그먼트는 주기 함수와 함께 수렴된다.

$h{\displaystyle \stackrel{}{}}$~${\displaystyle }$[ ${\displaystyle n}$ ${\displaystyle ]}$ ${\displaystyle {\tilde {h}[n]}$의 0이 아닌 값의 지속 시간이 < , ${\displaystyle M<N}$인 경우 출력 $시퀀스$에는 ${\displaystyle \stackrel{}{^}}$ .${\displaystyle {\$hat ${u}$의 N - M + 1 샘플이 포함된다.$}}$ N의 각 $블록$에서 M - 1 출력을 폐기하고, 입력 블록을 그 양만큼 겹쳐서 간격을 방지한다.

그림 5는 IIR 힐버트(·) 기능과 FIR 근사치를 모두 사용하는 예다. 이 예에서 사인 함수는 코사인 함수의 이산 힐버트 변환을 계산하여 생성되는데, 이 변환은 4개의 겹치는 세그먼트로 처리되었다가 다시 합쳐졌다. FIR 결과(파란색)에 나타난 바와 같이 IIR 결과(빨간색)에 나타난 왜곡은 h[n]와 h_N[n]의 차이(그림 3의 녹색과 적색)에 의한 것이 아니다. h_N[n]가 테이퍼(창문)되어 있다는 사실은 이런 맥락에서 실제로 도움이 된다. 진짜 문제는 창문이 충분히 열려 있지 않다는 것이다. 효과적으로, 중복 저장 방법에는 M < N이 필요한 반면, M = N.

Number-theoretic Hilbert transform

The number theoretic Hilbert transform is an extension^[50] of the discrete Hilbert transform to integers modulo an appropriate prime number. In this it follows the generalization of discrete Fourier transform to number theoretic transforms. The number theoretic Hilbert transform can be used to generate sets of orthogonal discrete sequences.^[51]

See also

• Analytic signal
• Harmonic conjugate
• Hilbert spectroscopy
• Hilbert transform in the complex plane
• Hilbert–Huang transform
• Kramers–Kronig relation
• Riesz transform
• Single-sideband signal
• Singular integral operators of convolution type

Notes

Page citations

References

Further reading

External links

Wikimedia Commons has media related to Hilbert transform.

• Derivation of the boundedness of the Hilbert transform
• Mathworld Hilbert transform — Contains a table of transforms
• Weisstein, Eric W. "Titchmarsh theorem". MathWorld.
• "GS256 Lecture 3: Hilbert Transformation" (PDF). Archived from the original (PDF) on 2012-02-27. an entry level introduction to Hilbert transformation.