고조파 직렬(수학)

수학에서 조화계열은 다이버전트 무한계열이다.

\sum_{n=1}^{\inflots.}{\frac {1}{1}{n1}:{n}+{1}{1}{1}{3}+{\frac {1}{1}}}{4}+{5}}}}}{5}+\frac {cdots.}}}}

그것의 이름은 음악에서 오버톤, 즉 고조파라는 개념에서 유래한다: 진동하는 문자열의 오버톤 파장은 문자열의 기본 파장의 1/2, 1/3, 1/4 등. 첫 번째 용어 이후 시리즈의 모든 용어는 이웃 용어의 조화 평균이다; 조화 평균도 마찬가지로 음악에서 유래한다.

역사

조화 시리즈의 분화는 니콜 오레스메에 의해 14세기에 처음으로 증명되었지만,^[1] 이 성과는 무명으로 떨어졌다. 증명서는 17세기에 피에트로 멘골리와^[2] 그의 형인 제이콥 베르누리에 의해 출판되고 대중화된 요한 베르누이에 의해 주어졌다.^[3]^[4]^[5]

역사적으로 조화로운 순서는 건축가들에게 일정한 인기를 끌었다. 이것은 바로크 시대에 건축가들이 평면도, 입면도, 입면도, 교회와 궁궐의 내외부 건축 디테일의 조화로운 관계를 확립하기 위해 그것들을 사용했던 매우 특별한 시기였다.^[6]

발산

고조파 계열의 분화에 대한 몇 가지 잘 알려진 증거가 있다. 그것들 중 몇 개는 아래에 제시되어 있다.

비교시험

분산을 증명하는 한 가지 방법은 고조파 계열을 다른 다이버전트 계열과 비교하는 것이다. 여기서 각 분모는 다음 두 개의 최대 전력으로 대체된다.

{\displaystyle{\begin{alignedat}{8}1&, +{\frac{1}{2}}&&+{\frac{1}{3}}&&+{\frac{1}{4}}&&+{\frac{1}{5}}&&+{\frac{1}{6}}&&+{\frac{1}{7}}&&+{\frac{1}{8}}&&+{\frac{1}{9}}&&+\cdots 1& \\[5pt]{}\geq, +{\frac{1}{2}}&&+{\frac{1}{\color{ 빨간}{\mathbf{4}}}}&&+{\fr.Ac{1}{4}}&&+{\frac{1}{\color{ 빨간}{\mathbf{8}}}}&&+{\frac{1}{\color{ 빨간}{\mathbf{.8} }}}&+{\frac {1}{\color {red}{\mathbf{8}}}}{\frac {1}{8}&+{\frac {1}{1}{\color {red}{\mathbf{16}}}&+\cdots \end{aignedat}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}?

고조파 계열의 각 항은 두 번째 계열의 해당 항보다 크거나 같으므로 고조파 계열의 합은 두 번째 계열의 합보다 크거나 같아야 한다. 그러나 두 번째 시리즈의 합은 무한하다.

{\begin{aligned}&1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}+{\frac {1}{4}}\right)+\left({\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right)+\left({\frac {1}{16}}+\cdots +{\frac {1}{16}}\right)+\cdots \\[5pt]{}}={}&1+{\frac{1}{1}:{2}}+{{1}:{1}:{2}}+{\frac{1}{1}:{1}:{1}:{1}:{1}:{1}{1}:{1}+\cdots =\inflineed}}}}}}}}}

(여기서, " = $=\infty$ { $=\infty$ {\ $displaystyle$ =\ $inflt$ $=\infty$ 은 시리즈의 부분 합계가 구속 없이 증가한다는 것을 나타내기 위한 논리에 불과하다.)

고조파 계열의 합도 무한해야 한다는 것을 (비교 시험에 의해) 따른다. 좀 더 정확히 말하자면, 위의 비교는 다음과 같은 것을 증명한다.

\sum _{n=1}^{2^{k}}{\frac{1}{n}}\geq 1+{\frac {k}{2}}:

모든 양의 정수 $k$ 에 대해.

니콜 오레스미가 1350년경에 제안한 이 증거는 수학계의^{[by whom?]} 많은 사람들에 의해 중세 수학의 고점으로 여겨지고 있다. 그것은 오늘날에도 수학 수업에서 가르치는 표준적인 증거다. 코치의 응축 테스트는 이 주장을 일반화한 것이다.

적분시험

통합 테스트의 그림.

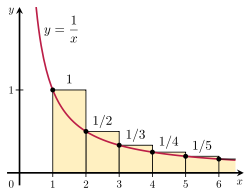
합을 부적합한 적분과 비교함으로써 고조파 계열의 분산을 증명할 수 있다. 특히 오른쪽 그림에 표시된 직사각형의 배열을 고려하십시오. 각 직사각형은 폭이 1단위이고 $높이$ 가1/ $n$ 이므로 무한 직사각형 수의 총 면적은 다음과 같은 고조파 계열의 합이다.

{\c}{c}{\text{rectangles}\end{array}}=1+{{1}{1}:{1}{1}{1}{3}+{\frac{1}}}{4}}}{5}}+\frac{5}+\cdots}}}}}}}

또한, $1$ 에서 무한대로의 y = $1$ / $x$ 곡선 아래의 총 영역은 다음과 같은 다양하고 부적절한 적분에 의해 주어진다.

{\c}{c}{c}{{\text{data}}\end{array}}=\int_{1}^{\flac{1}{x}\dx=\flass .}

이 영역은 직사각형 내에 완전히 포함되므로 직사각형의 전체 영역도 무한해야 한다. 더 정확히 말하면, 첫 $번째$ k $k$ 직사각형은 $k$ $1\leq x\leq k+1$ x $1\leq x\leq k+1$ $1\leq x\leq k+1$ + $1\leq x\leq k+1$ $1\leq x\leq k+1$ 의 $1\leq x\leq k+1$ 곡선 아래 영역을 완전히 덮는다.

\sum \sum _{n=1}^{1}{1}{n}}}\int_{1}^{k+1}{\frac{1}{x}\,dx=\ln(k+1).

이 주장의 일반화는 적분 시험으로 알려져 있다.

발산율

고조파 시리즈는 매우 천천히 분전한다. 예를 들어 처음 10개⁴³ 항의 합계가 100보다 작다.^[7] 시리즈물의 부분 합계가 로그 성장을 하기 때문이다. 특히.

\sum _{n=1}^{k}{\frac {1}{1}{n}=\ln k+\cHB +\varepsilon _{k}\leq(\ln k)+1

여기서 $γ$ 은 오일러-마스케로니 상수이고 $ε k$ ~1/ $2k$ 는 $k$ 가 무한대로 가면서 0에 접근한다. 레온하르트 오일러는 이 둘 다와 프리메스의 왕복만을 포함하는 합이 또한 분산된다는 더욱 놀라운 사실을 증명했다.^[8]

\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .

부분합

편차 고조파 계열의 유한 부분 합,

H_{n}=\sum _{k=1}^{n}{\frac {1}{k},

조화수라고 불린다.

$H$ 와_n $ln$ $n$ 의 차이는 오일러-마스케로니 상수로 수렴된다. 어떤 두 고조파 숫자의 차이는 결코 정수가 아니다. $H 1$ = $1$ 을 제외하고 어떤 고조파 숫자도 정수가 아니다.^[9]^{: p. 24}^[10]^{: Thm. 1}

관련 시리즈

교류 고조파 시리즈

교대 고조파 직렬(검은색 선 세그먼트)의 첫 14 부분 합계는 2의 자연 로그(빨간색 선)로 수렴되는 것을 보여주었다.

시리즈

\sum \{n=1}^{\frac {(-1)^{n1}:{n+1}{n1}:{n}=1-{1}{1}:{1}{1}{1}{3}-{\frac {1}}}{4}}+{\frac {1}{5}-cdots}}}}}}}}}

교류 고조파 시리즈로 알려져 있다. 이 시리즈는 교번 시리즈 시험에 의해 수렴된다. 특히 이 합계는 자연 로그인 2와 같다.

1-{\frac {1}{1}:{2}}+{{3}-{\frac {1}{1}:{4}}+{\frac {1}{1}{5}-\cdots =\ln 2.

교대 고조파 시리즈는 조건적으로 수렴되는 동안 절대적으로 수렴되지 않는다. 즉, 직렬의 용어들이 체계적으로 재배열되면 일반적으로 합계가 달라지고 재배열에 따라 무한정 될 수 있다.

교류 고조파 계열 공식은 메르카토르 계열의 특별한 경우, 자연 로그에 대한 테일러 계열이다.

아크탄젠트용 테일러 시리즈에서 관련 시리즈를 도출할 수 있다.

\sum \sum _{n=0}^{\frac {(-1)^{n}=1-{2n+1}{1}{3}+{{1}{5}-{5}-{\frac {1}{7}}}+\cdots={\frac {\pi}{4}}}}.

이것은 라이프니즈 시리즈로 알려져 있다.

일반 고조파 계열

일반 고조파 계열은 형식이다.

\sum _{n=0}^{\inflt }{\frac {1}{an+b},

여기서 ≠ $0$ 과 $b$ 는 실수이고, $b / a$ 는 0이나 음의 정수가 아니다.

고조파 계열과의 한계 비교 시험에 의해, 모든 일반 고조파 계열도 분화한다.

p-시리즈

고조파 영상 시리즈의 일반화는 p-영상 시리즈(또는 초화 영상 시리즈)로, 다음과 같이 정의된다.

\sum _{n=1}^{\inflt }{\frac {1}{n^{p}}}}}}

실제 번호 $p$ 에 대해. $p$ = $1일$ 때 p-시리즈는 고조파 계열로, 분리가 된다. 적분시험이나 Cauchy 응축시험에서는 $p-시리즈$ 가p > $1$ (이 경우 과화합성 시리즈라고 한다)에 모두 수렴하여 $p$ ≤ $1$ 에 대해 분산하는 것을 보여준다. $p$ > $1$ 이면 p-시리즈의 합은 $ζ (p),$ 즉 $p$ 에서 평가한 리만 제타함수이다.

$p$ = $2$ 의 합계를 구하는 문제를 바젤 문제라고 하는데, 레온하르트 오일러는 $그것$ 이² //6이라는 것을 보여주었다. 로저 아페리가 비이성적인 수라는 것을 증명했기 때문에 p = 3의 합계 값은 아페리의 상수라고 불린다.

ln 시리즈

p-시리즈와 관련된 것은 다음과 같이 정의되는 ln-시리즈이다.

\sum _{n=2}^{\inflt }{\frac {1}{n(\ln n)^{p}}}}}}}}}

모든 양의 실제 $번호$ p에 대해. $이$ 는 p ≤ $1$ 에 대해 분산되지만 모든 $p$ > $1$ 에 대해 수렴하기 위한 적분 시험으로 확인할 수 있다.

φ시리즈

모든 볼록, 실제 값 함수 $φ$ .

\limsup _{u\to 0^{+}{\frac {\varpi \refac {u}{2}}\right)}{\varpi (u)}}}{\frac {1}{1},},

시리즈

\sum _{n=1}^{\inflt }\varphi \lefts\frac {1}{n}\오른쪽)

수렴성이 있다.^{[citation needed]}

랜덤 고조파 시리즈

\sum _{n=1}^{\inflt }{\frac {s_{n}},

$s$ 가_n 독립적이고 동일한 분포의 랜덤 변수가 동일한 확률 1/2로 +1 및 -1 값을 취하는 경우, 확률 이론에서 확률 1과 수렴하는 일련의 랜덤 변수에 대한 잘 알려진 예다. 이러한 수렴의 사실은 콜모고로프 3계열 정리나 밀접하게 연관되어 있는 콜모고로프 최대불평등의 쉬운 결과다. 앨버타 대학의 바이런 슈물란드는 무작위 고조파 시리즈의 성질을 더 자세히^[11] 조사했고, 수렴 시리즈가 어떤 흥미로운 성질을 가진 무작위 변수라는 것을 보여주었다. 특히 +2 또는 -2에서 평가된 이 랜덤 변수의 확률밀도함수는 1/8에서 10보다⁻⁴² 작은 0.1249999999999999999999764 값을 차지한다. Schmuland의 논문은 왜 이 확률이 1/8에 가깝지만, 정확하지는 않은지에 대해 설명한다. 이 확률의 정확한 값은 무한 코사인 제품 적분 $C$ 를₂^[12] $π$ 으로 나눈 값이다.

고갈된 고조파 시리즈

분모의 아무 곳이나 숫자 9가 나타나는 모든 항이 제거되는 고갈된 고조파 시리즈는 값 22.92067661926415034816으로 수렴되는 것을 보여줄 수 있다....^[13] 실제로 어떤 특정한 숫자의 문자열을 포함하는 모든 용어(모든 베이스에서)가 제거되면 시리즈는 수렴된다.^[14]

적용들

$하모니$ 시리즈는 n번째의 한계가 0으로 무한대로 가더라도 서로 다른 시리즈이기 때문에 학생들이 처음 접하게 되는 직관에 반할 수 있다. 고조파 계열의 차이도 몇몇 명백한 역설의 근원이 된다. 이것의 한 예는 "고무대 위의 벌레"^[15]이다. 고무줄이 일률적으로 늘어나면서 무한탄력 1m 고무줄을 따라 벌레가 기어간다고 가정해보자. 지렁이가 분당 1cm씩 이동하고 띠가 분당 1m씩 늘어나면 지렁이가 고무줄 끝에 도달하는 일이 있을까. 역직적으로 답은 "네"이다. $n분$ 후, 고무줄의 총 길이에 대한 벌레가 이동한 거리의 비율은

{\frac {1}{100}\sum _{k=1}^{n}{\frac {1}{k}}.

(사실 밴드가 계속 확장되면서 실제 비율은 이 합계보다 조금 적다.)

$시리즈$ 는 n이 커질수록 임의로 커지기 때문에 결국 이 비율은 1을 초과해야 하는데, 이는 웜이 고무줄의 끝에 도달한다는 것을 의미한다. 그러나 이러한 현상이 발생하는 $n$ 의 값은 매우 커야 한다. 대략⁴³ e, 10분(10년³⁷)을¹⁰⁰ 초과하는 숫자. 비록 고조파 시리즈는 분리가 되지만, 매우 천천히 분리가 된다.

조화 시리즈와 관련된 또 다른 문제는 지프 문제인데, 이 문제는 (한 형태로) 사막을 건너는 데 연료 운반 용량이 제한적인 지프에게 총 연료가 얼마나 필요한지를 묻고, 노선을 따라 연료가 떨어질 수도 있다. 일정한 양의 연료로 횡단할 수 있는 거리는 로그적으로 성장하는 고조파 계열의 부분 합계와 관련이 있다. 따라서 필요한 연료는 원하는 거리에 따라 기하급수적으로 증가한다.

블록 쌓기 문제: 모든 폭의 고조파 직렬 브리지 분할에 따라 정렬된 블록.

또 다른 예는 블록 쌓기 문제인데, 동일한 도미노의 컬렉션을 볼 때, 그것들이 떨어지지 않고 테이블 가장자리에 걸려 있도록 테이블 가장자리에 쌓는 것이 분명히 가능하다. 역직관적 결과는 도미노가 충분하다면 오버행(overhang)을 임의로 크게 만드는 방식으로 쌓을 수 있다는 것이다.^[15]^[16]

반면에, 더 간단한 예는 수영장의 벽을 만질 때 계속해서 속도를 더하는 수영선수다. 수영 선수는 2m/s의 속도로 10m의 수영장을 건너기 시작하고, 모든 크로스를 할 때마다 2m/s가 더해진다. 이론적으로, 수영하는 사람의 속도는 무한하지만, 그 속도에 도달하기 위해 필요한 수영장 크로스의 수는 매우 커진다. 예를 들어, 빛의 속도에 도달하기 위해서는 수영하는 사람이 수영장을 1억 5천만 번 건너야 한다. 이 큰 숫자와는 달리, 주어진 속도에 도달하는 데 필요한 시간은 주어진 풀 크로스의 수(반복)에서 시리즈 합계에 따라 달라진다.

{\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.

총계(반복적으로)를 계산하면 빛의 속도에 도달하는 데 필요한 시간이 97초밖에 안 된다는 것을 알 수 있다. 이 지점(빛의 속도를 초과하여, 다시 특수 상대성을 무시함)을 넘어 계속됨으로써, 수영장을 가로지르는 데 걸리는 시간은 반복 횟수가 매우 커짐에 따라 사실상 0에 근접하게 되며, 수영장을 가로지르는 데 필요한 시간은 0(무한 반복 횟수에서)에 가까운 경향이 있지만, 반복의 합(시간 ta)은 0에 가까워지게 된다.총 풀 크로스를 위한 ken)은 여전히 매우 느린 속도로 갈릴 것이다.

참고 항목

참조

^ Oresme, Nicole (c. 1360). Quaestiones super Geometriam Euclidis [Questions concerning Euclid's Geometry].
^ Mengoli, Pietro (1650). "Praefatio [Preface]". Novae quadraturae arithmeticae, seu De additione fractionum [New arithmetic quadrature (i.e., integration), or On the addition of fractions]. Bologna: Giacomo Monti.
멘골리의 증거는 모순에 의한 것이다.
$S$ 는 시리즈의 합계를 나타내도록 하자. Group the terms of the series in triplets: $S = 1 + (1 / 2 + 1 / 3 + 1 / 4) + (1 / 5 + 1 / 6 + 1 / 7) + (1 / 8 + 1 / 9 + 1 / 10) + \dots$ Since for $x > 1$ , $1 / x - 1 + 1 / x + 1 / x + 1 > 3 / x$ , then $S > 1 + 3 / 3 + 3 / 6 + 3 / 9 + \dots = 1 + 1 + 1 / 2 + 1 / 3 + \dots = 1 + S$ , which is false for any finite $S$ . 따라서 시리즈는 갈라진다.
^ Bernoulli, Johann (1742). "Corollary III of De seriebus varia". Opera Omnia. Lausanne & Basel: Marc-Michel Bousquet & Co. vol. 4, p. 8.
요한 베르누이의 증거도 모순에 의한 것이다. 각 용어 1/n을 다음과 같이 나타내는 텔레스코픽 합을 사용한다.
${\frac {1}{n}}={\Big (}{\frac {1}{n}}-{\frac {1}{n+1}}{\Big )}+{\Big (}{\frac {1}{n+1}}-{\frac {1}{n+2}}{\Big )}+{\Big (}{\frac {1}{n+2}}-{\frac {1}{n+3}}{\Big )},\&c.$ $={\frac {1}{n(n+1)}+{\frac {1}{(n+1){{(n+1)}}}}}{\frac {1}{(n+2)(n+3)}}}}},\&c.$
현대 표기법에서 해당 이중 시리즈에서 합계의 순서 변경
$S=\sum _{n=1}^{\infty }{\frac {1}{n}}=\sum _{n=1}^{\infty }\sum _{k=n}^{\infty }{\frac {1}{k(k+1)}}=\sum _{k=1}^{\infty }\sum _{n=1}^{k}{\frac {1}{k(k+1)}}$ $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ ) $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ = $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ = $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ 1 $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ + 1 $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ = S $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ - $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ ${\displaystyle =\sum$ =\sum $_{k=1}^{k(k+1)}{\prac {k}{k$ =1 $}}}}=\sum _{k=1}^{k+1}=S-1$
^ Bernoulli, Jacob (1689). Propositiones arithmeticae de seriebus infinitis earumque summa finita [Arithmetical propositions about infinite series and their finite sums]. Basel: J. Conrad.
^ Bernoulli, Jacob (1713). Ars conjectandi, opus posthumum. Accedit Tractatus de seriebus infinitis [Theory of inference, posthumous work. With the Treatise on infinite series…]. Basel: Thurneysen. pp. 250–251.
250페이지부터, 소품. 16:
"XVI. Suma serei infinita harmonica generalium, 1/1 + 1/2 + 1/3 + 1/4 + 1/5 &c. est infinita. 프리머스 딘은 동료들을 체포했다.…"

[16. 조화진행의 무한 계열의 합, 1/1 + 1/2 + 1/3 + 1/4 + 1/5 + …은 무한하다. 오빠는 이것을 처음 발견했다…]
^ Hersey, George L. Architecture and Geometry in the Age of the Baroque. pp. 11–12, 37–51.
^ Sloane, N. J. A. (ed.). "Sequence A082912 (Sum of a(n) terms of harmonic series is > 10ⁿ)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Euler, Leonhard (1737). "Variae observationes circa series infinitas" [Various observations concerning infinite series]. Commentarii Academiae Scientiarum Petropolitanae. 9: 160–188.
^ 줄리안 하빌, 감마: 2009년 프린스턴 대학 출판부의 오일러 상수 탐사.
^ 토마스 J. 오슬러, "정수가 될 수 없는 부분적인 시리즈의 합계" , The Mathematical Gazette 96, 2012년 11월, 515–519. https://www.jstor.org/stable/24496876?seq=1#page_scan_tab_contents
^ Schmuland, Byron (May 2003). "Random Harmonic Series" (PDF). American Mathematical Monthly. 110 (5): 407–416. doi:10.2307/3647827. JSTOR 3647827.
^ Weisstein, Eric W. "Infinite Cosine Product Integral". MathWorld. Retrieved November 9, 2020.
^ Robert Baillie (May 1979). "Sums of Reciprocals of Integers Missing a Given Digit". The American Mathematical Monthly. 86 (5): 372–374. doi:10.1080/00029890.1979.11994810. JSTOR 2321096.
^ Thomas Schmelzer and Robert Baillie (Jun 2008). "Summing a Curious, Slowly Convergent Series". The American Mathematical Monthly. 115 (6): 545–540. JSTOR 27642532.
^ ^a ^b Graham, Ronald; Knuth, Donald E.; Patashnik, Oren (1989), Concrete Mathematics (2nd ed.), Addison-Wesley, pp. 258–264, ISBN 978-0-201-55802-9
^ Sharp, R. T. (1954). "Problem 52: Overhanging dominoes" (PDF). Pi Mu Epsilon Journal. 1 (10): 411–412.

외부 링크

"Harmonic series", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
"The Harmonic Series Diverges Again and Again" (PDF). The AMATYC Review. 27: 31–43. 2006.
Weisstein, Eric W. "Harmonic Series". MathWorld.
Weisstein, Eric W. "Book Stacking Problem". MathWorld.
Hudelson, Matt (1 October 2010). "Proof Without Words: The Alternating Harmonic Series Sums to ln 2" (PDF). Mathematics Magazine. 83 (4): 294. doi:10.4169/002557010X521831. S2CID 119484945.

[1] Oresme, Nicole (c. 1360). Quaestiones super Geometriam Euclidis [Questions concerning Euclid's Geometry].

[2] Mengoli, Pietro (1650). "Praefatio [Preface]". Novae quadraturae arithmeticae, seu De additione fractionum [New arithmetic quadrature (i.e., integration), or On the addition of fractions]. Bologna: Giacomo Monti.
멘골리의 증거는 모순에 의한 것이다.
$S$ 는 시리즈의 합계를 나타내도록 하자. Group the terms of the series in triplets: $S = 1 + (1 / 2 + 1 / 3 + 1 / 4) + (1 / 5 + 1 / 6 + 1 / 7) + (1 / 8 + 1 / 9 + 1 / 10) + \dots$ Since for $x > 1$ , $1 / x - 1 + 1 / x + 1 / x + 1 > 3 / x$ , then $S > 1 + 3 / 3 + 3 / 6 + 3 / 9 + \dots = 1 + 1 + 1 / 2 + 1 / 3 + \dots = 1 + S$ , which is false for any finite $S$ . 따라서 시리즈는 갈라진다.

[3] Bernoulli, Johann (1742). "Corollary III of De seriebus varia". Opera Omnia. Lausanne & Basel: Marc-Michel Bousquet & Co. vol. 4, p. 8.
요한 베르누이의 증거도 모순에 의한 것이다. 각 용어 1/n을 다음과 같이 나타내는 텔레스코픽 합을 사용한다.
${\frac {1}{n}}={\Big (}{\frac {1}{n}}-{\frac {1}{n+1}}{\Big )}+{\Big (}{\frac {1}{n+1}}-{\frac {1}{n+2}}{\Big )}+{\Big (}{\frac {1}{n+2}}-{\frac {1}{n+3}}{\Big )},\&c.$ $={\frac {1}{n(n+1)}+{\frac {1}{(n+1){{(n+1)}}}}}{\frac {1}{(n+2)(n+3)}}}}},\&c.$
현대 표기법에서 해당 이중 시리즈에서 합계의 순서 변경
$S=\sum _{n=1}^{\infty }{\frac {1}{n}}=\sum _{n=1}^{\infty }\sum _{k=n}^{\infty }{\frac {1}{k(k+1)}}=\sum _{k=1}^{\infty }\sum _{n=1}^{k}{\frac {1}{k(k+1)}}$ $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ ) $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ = $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ = $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ 1 $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ + 1 $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ = S $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ - $=\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1$ ${\displaystyle =\sum$ =\sum $_{k=1}^{k(k+1)}{\prac {k}{k$ =1 $}}}}=\sum _{k=1}^{k+1}=S-1$

[4] Bernoulli, Jacob (1689). Propositiones arithmeticae de seriebus infinitis earumque summa finita [Arithmetical propositions about infinite series and their finite sums]. Basel: J. Conrad.

[5] Bernoulli, Jacob (1713). Ars conjectandi, opus posthumum. Accedit Tractatus de seriebus infinitis [Theory of inference, posthumous work. With the Treatise on infinite series…]. Basel: Thurneysen. pp. 250–251.
250페이지부터, 소품. 16:
"XVI. Suma serei infinita harmonica generalium, 1/1 + 1/2 + 1/3 + 1/4 + 1/5 &c. est infinita. 프리머스 딘은 동료들을 체포했다.…"

[16. 조화진행의 무한 계열의 합, 1/1 + 1/2 + 1/3 + 1/4 + 1/5 + …은 무한하다. 오빠는 이것을 처음 발견했다…]

[6] Hersey, George L. Architecture and Geometry in the Age of the Baroque. pp. 11–12, 37–51.

[7] Sloane, N. J. A. (ed.). "Sequence A082912 (Sum of a(n) terms of harmonic series is > 10ⁿ)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.

[8] Euler, Leonhard (1737). "Variae observationes circa series infinitas" [Various observations concerning infinite series]. Commentarii Academiae Scientiarum Petropolitanae. 9: 160–188.

[9] 줄리안 하빌, 감마: 2009년 프린스턴 대학 출판부의 오일러 상수 탐사.

[10] 토마스 J. 오슬러, "정수가 될 수 없는 부분적인 시리즈의 합계" , The Mathematical Gazette 96, 2012년 11월, 515–519. https://www.jstor.org/stable/24496876?seq=1#page_scan_tab_contents

[11] Schmuland, Byron (May 2003). "Random Harmonic Series" (PDF). American Mathematical Monthly. 110 (5): 407–416. doi:10.2307/3647827. JSTOR 3647827.

[12] Weisstein, Eric W. "Infinite Cosine Product Integral". MathWorld. Retrieved November 9, 2020.

[13] Robert Baillie (May 1979). "Sums of Reciprocals of Integers Missing a Given Digit". The American Mathematical Monthly. 86 (5): 372–374. doi:10.1080/00029890.1979.11994810. JSTOR 2321096.

[14] Thomas Schmelzer and Robert Baillie (Jun 2008). "Summing a Curious, Slowly Convergent Series". The American Mathematical Monthly. 115 (6): 545–540. JSTOR 27642532.

[autogenerated258-15] Graham, Ronald; Knuth, Donald E.; Patashnik, Oren (1989), Concrete Mathematics (2nd ed.), Addison-Wesley, pp. 258–264, ISBN 978-0-201-55802-9

[16] Sharp, R. T. (1954). "Problem 52: Overhanging dominoes" (PDF). Pi Mu Epsilon Journal. 1 (10): 411–412.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

$n$	고조파 $계열$ 의_n 부분 합계 H
$n$	분수로 표현된		십진법의	상대적 크기
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Search