균일 연속성

The graph of

f(x)={\tfrac {1}{x}}

escapes the top and/or bottom of the

{\text{height}}\times {\text{width}}=2\varepsilon \times 2\delta

window, however small the

\delta

, so

f(x)

is not unifor연속된반면 함수

g(x)={\sqrt {x}}

(

g(x)={\sqrt {x}}

)

g(x)={\sqrt {x}}

=

g(x)={\sqrt {x}}

{\

는 균일하게 연속적이다.

수학에서 f(x)와 f(y) 사이의 최대 거리가 x(x)와 y 자체에 의존할 수 있는 일반적인 연속성과 달리, 대략적으로 말하면, f(x)와 f(y)가 x(y) 그 자체에 충분히 근접하도록 요구함으로써 f(x)와 f(y)가 우리가 원하는 만큼 서로 근접하도록 보장할 수 있다면 함수 f(x)는 균일하게 연속된다.

연속함수는 ( $f(x)={\tfrac {1}{x}}$ ,1)에서 $f(x)={\tfrac {1}{x}}$ $f(x)={\tfrac {1}{x}}$ ( x $f(x)={\tfrac {1}{x}}$ ) $f(x)={\tfrac {1}{x}}$ = 1 $f(x)={\tfrac {1}{x}}$ ${\$ 와 같이 경계된 도메인에서 바인딩되지 않거나, 또는 $f(x)=x^{2}$ 의 경사가 f $f(x)=x^{2}$ ( $f(x)=x^{2}$ ) $f(x)=x^{2}$ = $f(x)=x^{2}$ $f(x)=x^{2}$ ${\$ 와 같은 $f(x)=x^{2}$ 무한 도메인에서 바인딩된 경우, 균일하게 연속되지 않을 수 있다.그러나 미터법 공간 사이의 모든 립스치츠 맵은 균일하게 연속적이며, 특히 등거리 측정(거리 보존 맵)이 있다.

일반적인 위상학적 공간 사이의 기능에 대해 통상적인 연속성을 정의할 수 있지만, 균일한 연속성을 정의하는 것은 더 많은 구조를 필요로 한다.개념은 구별되는 점의 인접 지역의 크기를 비교하는 것에 의존하기 때문에 미터법 공간, 또는 보다 일반적으로 균일한 공간이 필요하다.

메트릭 공간의 함수에 대한 정의

계량 공간(X, 1d){\displaystyle(X,d_{1})}과(Y, d2){\displaystyle(Y,d_{2})}, 함수 f:X→ Y{\displaystyle f:X\to Y}은 모든 실수 ε>0에{\displaystyle \varepsilon>0}, 실제 δ 을 존재하는 평등 연속,라고 불리는 0{\displaystyle \delta>0}이다. 는 f와 같은또는 $d_{1}(x,y)<\delta$ $x,y\in X$ , $x,y\in X$ $x,y\in X$ $d_{1}(x,y)<\delta$ $x,y\in X$ {\ $d_{1}(x,y)<\delta$ $x,y\in$ X $d_{1}(x,y)<\delta$ $d_{1}(x,y)<\delta$ 1 $d_{1}(x,y)<\delta$ ( $d_{1}(x,y)<\delta$ , y $d_{1}(x,y)<\delta$ ) Δ {\ $displaystyle$ d_ ${1}(x$ $d_{2}(f(x),f(y))<\varepsilon$ $)$ , $d_{2}(f(x),f(y))<\varepsilon$ f $d_{2}(f(x),f(y))<\varepsilon$ ( $d_{2}(f(x),f(y))<\varepsilon$ $d_{2}(f(x),f(y))<\varepsilon$ $d_{2}(f(x),f(y))<\varepsilon$ $d_{2}(f(x),f(y))<\varepsilon$ $($ f $(y)<varepsilon$ $d_{2}(f(x),f(y))<\varepsilon$ $d)$ 가 있다 $d_{2}(f(x),f(y))<\varepsilon$

진짜 라인, 1과 d2 중 만약 X와 Y은 하위 집합이 될 수 있는 표준 1차원 유클리드 거리, 정의 항복:모든ε>0에{\displaystyle \varepsilon>0}이 δ 을 존재하는 모든 x, y∈ X를 0{\displaystyle \delta>0}가)− y<>δ ⟹ f())− f(y)<>ε{\di.splaystyle x,y\in X, $x-y <\cHB \implies f(x)-f(y) <\varepsilon$ $x,y\in X,|x-y|<\delta \implies |f(x)-f(y)|<\varepsilon$

모든 지점에서 동일한 연속성과 일반적인 연속성의 차이는 $\delta$ $\delta$ 의 값이 $\varepsilon$ $\varepsilon$ 에만 의존하고 $\delta$ $\varepsilon$ 도메인의 포인트에는 의존하지 않는다는 것이다.

로컬 연속성 대 글로벌 균일 연속성

연속성 그 자체는 함수의 국부적 속성이다. 즉, 함수 f는 특정 지점에서 연속적이거나 그렇지 않으며, 이는 해당 지점의 (임의적으로 작은) 인접 지역에서 함수의 값만을 보고 결정할 수 있다.우리가 어떤 함수가 어떤 간격에 연속되어 있다고 말할 때, 우리는 단지 그 간격의 각 지점에서 연속된다는 것을 의미한다.대조적으로, 균일한 연속성은 표준 정의가 개별 점보다는 점의 쌍을 참조한다는 점에서 f의 글로벌 속성이다.한편, 임의의 초현실 가치 함수에 대해 통일된 연속성의 로컬 정의를 제공할 수는 없지만, 자연적 확장 f*(비표준 지점의 특성은 f의 글로벌 속성에 의해 결정됨) 측면에서 국부적인 정의를 내릴 수 있다(아래 참조).

함수가 구간 I에 연속적이라는 수학적 설명과 함수가 동일한 구간에서 균일하게 연속된다는 정의는 구조적으로 매우 유사하다.따라서 간격의 모든 점 x에 대한 함수의 연속성은 정량화로 시작하는 공식으로 표현할 수 있다.

\displaystyle \forall x\in I\;\exists \varepsilon >0\;\fall y\in I:\, x-y <\delta \,\Rightarrow \, f(x)-f(y) <\varepsilon \...}

균일한 연속성을 위해 첫 번째, 두 번째 및 세 번째 정량자의 순서가 회전한다.

\displaystyle \for \varepsilon >0\;\exists \delta >0\;\fall x\in I:\, x-y <\delta \,\Rightarrow \, f(x)-f(y) <\varepsilon }}

따라서 각 지점에서 연속성을 위해 임의의 점 x를 취하며, 그 다음에는 거리 Δ가 존재해야 한다.

\displaystyle \cdots \forall x\,\flash \cdots \cdots,}

균일한 연속성을 위해 단일 Δ는 모든 x (및 y):

\displaystyle \cdots \cdots \cdots \cd \forall x\,\all y\cdots .}

예제 및 counterexample

두 메트릭스 공간 사이의 모든 립스치츠 연속 지도는 균일하게 연속적이다.특히, 구별이 가능하고 파생상품이 한정된 모든 기능은 균일하게 연속적이다.보다 일반적으로 모든 쾰더 연속 기능은 균일하게 연속적이다.
전혀 다른 점이 없음에도 불구하고 Weierstrass 기능은 균일하게 연속적이다.
균일하게 동일한 기능의 모든 구성원은 균일하게 연속적이다.
접선 함수는 간격(-through/2, π/2)에 연속적이지만, 그 간격에 대해 균일하게 연속되지 않는다.
지수함수 x $\scriptstyle \mapsto$ ${\$ 는 $\scriptstyle \mapsto$ ^x 실제 라인의 모든 곳에서 연속적이지만 라인에서는 균일하게 연속되지 않는다.

특성.

모든 균일하게 연속되는 기능은 연속적이지만, 역은 유지되지 않는다.Consider for instance the function $f\colon \mathbb {R} \rightarrow \mathbb {R} ,x\mapsto x^{2}$ . Given an arbitrarily small positive real number $\varepsilon$ , uniform continuity requires the existence of a positive number $\delta$ such that for $|x_{1}-x_{2}|<\delta$ $x_{1},x_{2}$ $x_{1},x_{2}$ , $x_{1},x_{2}$ $x_{1},x_{2}$ ${\$ x $|x_{1}-x_{2}|<\delta$ - $|x_{1}-x_{2}|<\delta$ $|x_{1}-x_{2}|<\delta$ < $|x_{1}-x_{2}|<\delta$ ${\displaystyle x_{1}-x_{2$ $|f(x_{1})-f(x_{2})|<\varepsilon$ ( $|f(x_{1})-f(x_{2})|<\varepsilon$ $|f(x_{1})-f(x_{2})|<\varepsilon$ ) $|f(x_{1})-f(x_{2})|<\varepsilon$ ${\displaysty f(x_{1}-{$ 2})- $f(x_{2})-{varepsilon }$ 이 있지만 $|f(x_{1})-f(x_{2})|<\varepsilon$

f\left(x+{\frac {}{2}}\\오른쪽)-f(x)=2x\cdot {\frac {\reason }{2}}+{\frac {\frac ^{4},},

그리고 충분히 큰 x에 대해 이 양은 $\varepsilon$ $\varepsilon$ 보다 크다 $\varepsilon$

절대적으로 연속적인 기능은 균일하게 연속적이다.반면에 칸토어 기능은 균일하게 연속적이지만 절대적으로 연속되지는 않는다.

균일하게 연속되는 함수 하에서 완전히 경계된 부분 집합의 이미지는 완전히 경계된다.그러나, 균일 연속 함수 하에서 임의의 메트릭 공간의 경계 부분 집합의 이미지는 경계가 필요하지 않다. 즉, 개별 메트릭을 부여한 정수에서 일반적인 유클리드 메트릭을 부여한 정수까지 식별 함수를 고려한다.

하이네-칸토르 정리는 콤팩트 세트의 모든 연속적 기능이 균일하게 연속적이라고 주장한다.특히 함수가 실선의 폐쇄된 경계 구간에서 연속되는 경우, 그 구간에서 균일하게 연속된다.연속함수의 Darboux 통합성은 거의 즉시 이 정리로부터 따른다.

$실제$ 값 함수 $f$ ${\displaystyle$ $f}$ 이 $[0,\infty )$ 가) [ $[0,\infty )$ , $[0,\infty )$ ) $[0,\inflt )$ 에 $[0,\infty )$ 연속적이고 $f$ $\lim _{x\to \infty }f(x)$ x $\lim _{x\to \infty }f(x)$ → $\lim _{x\to \infty }f(x)$ $\lim _{x\to \infty }f(x)$ ) $\lim _{x\to \infty }f(x)$ {\ $displaystyle \{x\to \inf(x)}$ 이 $\lim _{x\to \infty }f(x)$ (가 유한한 경우, f ${\$ displaystystystyf})가 균일하게 연속적이다 $f$ .특히 무한대에서 사라지는 $\mathbb {R}$ $\mathbb {R}$ ${\$ 의 연속 함수 공간인 $C_{0}(\mathbb {R} )$ C $R$ ) ${\$ displaystyle \mathb {R $}}$ 의 모든 요소는 균일하게 연속적이다. $C_{c}(\mathbb {R} )\subset C_{0}(\mathbb {R} )$ $C_{c}(\mathbb {R} )\subset C_{0}(\mathbb {R} )$ ( $C_{c}(\mathbb {R} )\subset C_{0}(\mathbb {R} )$ ) $C_{c}(\mathbb {R} )\subset C_{0}(\mathbb {R} )$ ⊂ C $C_{c}(\mathbb {R} )\subset C_{0}(\mathbb {R} )$ ( $C_{c}(\mathbb {R} )\subset C_{0}(\mathbb {R} )$ ) $C_{c}(\mathb {R})\subset C_{0}(\mathb {R$ ) $C_{c}(\mathbb {R} )\subset C_{0}(\mathbb {R} )$ since 이후 $C_{c}(\mathbb {R} )\subset C_{0}(\mathbb {R} )$ 위에서 언급한 하이네-칸토르 정리의 일반화다.

시각화

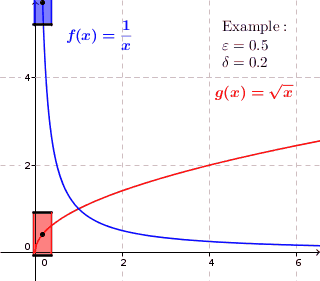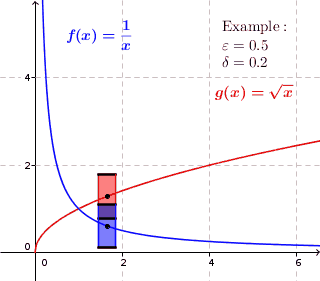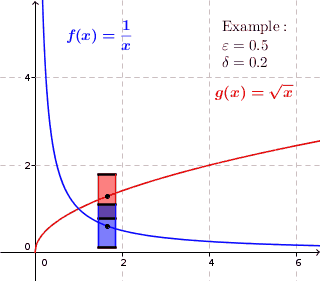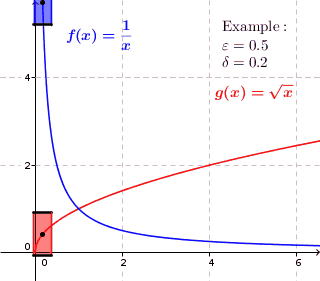
균일하게 연속 함수에는 모든 주어진 ε 을, 0은 δ 을{\displaystyle \varepsilon>0};0{\displaystyle \delta>0}가 두 값 조의()){\displaystyle f())}와 f(y){\displaystyle f(y)} 때마다){\displays{\displaystyle \varepsilon}최대 거리 ε 것이다.tyle x}d $y$ do not differ for more than $\delta$ . Thus we can draw around each point $(x,f(x))$ of the graph a rectangle with height $2\varepsilon$ and width $2\delta$ so that the graph lies completely inside the re바로 위나 아래에 있지 않고, 절개한다.균일하게 연속되지 않는 함수의 경우, 이것은 불가능하다.그래프는 그래프의 특정 중간점을 위해 직사각형 안에 위치할 수 있지만, 함수가 직사각형 위 또는 아래에 있는 그래프에는 항상 직사각형의 중간점이 있다.

평등 연속 기능은 각 ε 을, 0은 δ 을{\displaystyle \varepsilon>0};0{\displaystyle \delta>0} 때 그래프의 각 지점에서 폭 2δ{2\delta\displaystyle}과 높이 2ε{2\varepsilon\displaystyle}로 사각형 그리는 그래프 거짓말 같은 완전히 구석 있다.ide은 rect각
는 평등 연속지 않은 기능을 위해, 그곳에는ε>0{\displaystyle \varepsilon>0}은 관계 없이 δ의;0{\displaystyle \delta>0}은 항상 그래프에서 점, 우리가 둘러싸고 있는 2ε×2δ{\displaystyle 2\varepsilon \times 2\delta}사각형 그리기, 값을 직접 있다 하나다.bove 또는 below 직사각형.그래프가 직사각형 안에 완전히 들어 있는 중간점이 있을 수 있지만 모든 중간점에 대해서는 그렇지 않다.

역사

균일한 연속성에 대한 최초의 공식적 정의는 1870년 하이네이에 의해 발표되었으며, 1872년 그는 개방된 간격의 연속적 함수가 균일하게 연속적일 필요는 없다는 증거를 발표했다.그 증거는 디리클레트가 1854년 명확한 통합에 대한 그의 강의에서 준 거의 완전한 의견이다.균일한 연속성의 정의는 볼자노의 작업 초기에 나타나는데, 그는 또한 개방된 간격의 연속적인 기능이 균일하게 연속적일 필요가 없다는 것을 증명했다.덧붙여 그는 닫힌 간격의 연속함수는 균일하게 연속함수지만, 완전한 증거를 제시하지는 않는다고도 진술하고 있다.^[1]

기타 특성

비표준분석

비표준 분석에서 실제 변수의 실제 값 함수 f는 Δ가 최소일 때마다 f*(a + Δ) - f*(a)의 차이가 최소인 경우 정확히 한 점에서 마이크로 연속적이다.따라서 f*가 모든 실제 지점 a ∈ A에서 마이크로 연속인 경우 정확히 R의 세트 A에서 f가 연속된다.균일한 연속성은 (자연확장)f가 A의 실제 지점뿐만 아니라 R의 비표준 상대(자연확장) A의 모든 지점에서 미세연속적이라는 조건으로 표현할 수 있다.이 기준을 충족하지만 균일하게 연속되지 않는 초현실 가치 함수와 이 기준을 충족하지 않는 균일하게 연속된 초현실 가치 함수가 존재한다는 점에 유의하십시오. 그러나 이러한 함수는 어떤 실제 가치 함수 f에 대해서도 f* 형식으로 표현할 수 없다(자세한 내용과 예는 비표준 미적분 참조).).

코치 연속성

미터법 공간 사이의 함수의 경우, 균일한 연속성은 Cauchy 연속성을 의미한다(Fitzpatrick 2006).구체적으로는 A를 R의ⁿ 서브셋으로 한다.함수 f : A → R이^m 균일하게 연속적인 경우, 모든 시퀀스 쌍 x와_n y에_n 대해 다음과 같은 값을 적용한다.

\lim _{n\to \infit }x_{n}-y_{n} =0

우리는 가지고 있다.

\lim _{n\to \infit }f(x_{n}-f(y_{n}) =0.

연장 문제와의 관계

X를 미터법 공간으로 하고, S를 X의 서브셋으로 하고, R을 완전한 미터법 공간으로 하고, $f:S\rightarrow R$ : S $f:S\rightarrow R$ → $f:S\rightarrow R$ ${\displaystyle f:$ $S\오른쪽$ 화살표 $R}$ 은 $f:S\rightarrow R$ (는)언제 모든 X에서 f를 연속 함수로 확장할 수 있는가?

X에서 S가 닫히면, 대답은 티에체 확장 정리:항상:에 의해 주어진다.따라서 X에서 S의 폐쇄까지 f를 연장하는 것은 필요하며 충분하다. 즉, 우리는 일반성을 잃지 않고 S가 X에 밀도가 있다고 가정할 수 있다. 이는 확장이 존재한다면 그것이 유일하다는 더 유쾌한 결과를 낳는다.f가 연속 함수 $f:X\rightarrow R$ : $f:X\rightarrow R$ → $f:X\rightarrow R$ ${\displaystyle f:X\rightarrow$ R $}$ 까지 확장하기에 충분한 조건은 $f:X\rightarrow R$ Cauchy-연속적이라는 것이다. 즉, Cauchy 시퀀스의 f 아래에 있는 이미지는 Cauchy로 남아 있다.X가 완전하면(따라서 S가 완성되면), X에서 미터법 공간 Y까지 모든 연속 함수는 Cauchy-연속이다.따라서 X가 완료되면 f는 $f:X\rightarrow R$ 연속 함수 f : X → $f:X\rightarrow R$ ${\displaystyle f:X\오른쪽$ 화살표 R}( $f가$ Cauchy-연속인 경우에만 $f:X\rightarrow R$ 해당)로 확장된다.

모든 균일하게 연속되는 기능이 Cauchy-연속성이므로 X까지 확장되는 것을 쉽게 알 수 있다. $f:R\rightarrow R,x\mapsto x^{2}$ f $f:R\rightarrow R,x\mapsto x^{2}$ : $f:R\rightarrow R,x\mapsto x^{2}$ → $f:R\rightarrow R,x\mapsto x^{2}$ , $f:R\rightarrow R,x\mapsto x^{2}$ $f:R\rightarrow R,x\mapsto x^{2}$ $f:R\rightarrow R,x\mapsto x^{2}$ $f:R\rightarrow R,x\mapsto x^{2}$ ${\$ $R\rightarrow R,x\mapsto$ x $^{2}}$ 은 $f:R\rightarrow R,x\mapsto x^{2}$ 위에서 본 바와 같이 균일하게 연속되지 않고 연속적이며 따라서 Cauchy가 연속적이다.일반적으로 R과 같은 무한 공간에 정의된 기능의 경우 균일한 연속성은 다소 강한 조건이다.확장성을 추론할 수 있는 조건이 약한 것이 바람직하다.

예를 들어, > 1이 실제 숫자라고 가정합시다.프리컬러스 수준에서 함수 $f:x\mapsto a^{x}$ : $f:x\mapsto a^{x}$ ↦ $f:x\mapsto a^{x}$ ${\$ a $^{x}}$ 는 x의 합리적인 값에 대해서만 정확한 정의를 내릴 수 있다 $f:x\mapsto a^{x}$ (양수 실수의 q번째 루트의 존재, 중간값 정리의 적용).하나는 모든 R에 정의된 함수로 f를 확장하고자 한다.아이덴티

f(x+\properties )-f(x)=a^{x}\왼쪽(a^{\properties }-1\오른쪽)

f는 모든 합리적인 숫자의 정해진 Q에 대해 균일하게 연속되지 않음을 보여준다. 그러나 경계 I에 대해 f와 Q $Q\cap I$ I $Q\cap I$ {\ $displaystyle Q\cap$ I $}$ 의 제한은 균일하게 연속적이므로 $Q\cap I$ , 따라서 Cauchy-연속성이며, 따라서 f는 I에 대한 연속 함수로 확장된다.그러나 이것은 모든 I를 지탱하기 때문에, 모든 R에 대해 f의 고유한 확장이 있다.

보다 일반적으로 연속함수 $f:S\rightarrow R$ : $f:S\rightarrow R$ → R ${\displaystyle f:$ S의 모든 경계 부분 집합에 대한 제한이 균일하게 지속되는 $f:S\rightarrow R$ $S\오른쪽$ 화살표 $R}$ 은(는) X까지 확장할 수 있으며, X가 국소적으로 압축된 경우 역이 유지된다.

균일 연속함수의 확장성의 전형적인 적용은 역 푸리에 변환식의 증명이다.우리는 먼저 그 공식이 시험 기능에 대한 진실임을 증명한다. 그것들 중 많은 것들이 밀집되어 있다.그런 다음 선형 지도가 연속적이라는 사실을 사용하여 역지도를 전체 공간으로 확장한다. 따라서 균일하게 연속된다.

위상 벡터 공간에 대한 일반화

위상 벡터 공간 $V$ $V$ $W$ W $W$ 의 특별한 경우 $W$ 지도 $f:V\to W$ 의 균일한 연속성 개념 $f:V\to W$ : $f:V\to W$ → W ${\displaystyle f:$ $V\to W}$ becomes: for any neighborhood $B$ of zero in $W$ , there exists a neighborhood $A$ of zero in $V$ such that $v_{1}-v_{2}\in A$ implies ${\displaystyle f(v_{1})-$ $f(v_{2})\in B.$ $}$

선형 변환 $f:V\to W$ : $f:V\to W$ → W ${\displaystyle f:$ $V\to W$ 균일한 연속성은 연속성과 동등하다.이 사실은 바나흐 공간의 밀도 높은 하위 공간에서 선형 지도를 확장하기 위해 기능 분석에서 암묵적으로 자주 사용된다.

균일한 공간에 대한 일반화

연속성에 대한 가장 자연적이고 일반적인 설정이 위상학적 공간인 것처럼, 균일한 연속성에 대한 연구를 위한 가장 자연적이고 일반적인 설정은 균일한 공간이다.균일한 공간 사이의 함수 f : X → Y는 Y의 모든 수행자 V에 우리가 V에 (f(x₁), f(x₂)를 가지고 있는 (x₁, x₂)의 수행자 U가 X에 존재한다면 균일하게 연속적이라고 불린다.

이 설정에서, 균일하게 연속되는 지도는 Cauchy 시퀀스를 Cauchy 시퀀스로 변환하는 것도 사실이다.

각각의 콤팩트한 하우스도르프 공간은 토폴로지와 호환되는 정확히 하나의 균일한 구조를 가지고 있다.그 결과는 하이네-칸토르 정리의 일반화다. 컴팩트한 하우스도르프 공간에서 균일한 공간에 이르기까지 각각의 연속적인 기능은 균일하게 연속적이다.

참고 항목

균일 이형성 – 균일하게 연속된 동형성

참조

^ 러스노크 & 커-로슨 2005.

추가 읽기

Bourbaki, Nicolas. General Topology: Chapters 1–4 [Topologie Générale]. ISBN 0-387-19374-X. 제2장은 균일한 공간에 대한 포괄적인 참고문헌이다.
Dieudonné, Jean (1960). Foundations of Modern Analysis. Academic Press.
Fitzpatrick, Patrick (2006). Advanced Calculus. Brooks/Cole. ISBN 0-534-92612-6.
Kelley, John L. (1955). General topology. Graduate Texts in Mathematics. Springer-Verlag. ISBN 0-387-90125-6.
Kudryavtsev, L.D. (2001) [1994], "Uniform continuity", Encyclopedia of Mathematics, EMS Press
Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. ISBN 978-0-07-054235-8.
Rusnock, P.; Kerr-Lawson, A. (2005), "Bolzano and uniform continuity", Historia Mathematica, 32 (3): 303–311, doi:10.1016/j.hm.2004.11.003

[FOOTNOTERusnockKerr-Lawson2005-1] 러스노크 & 커-로슨 2005.

[1]

Search