엔벨로프(파형)
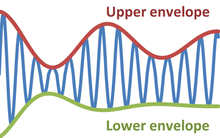
Envelope (waves)물리학과 공학에서 진동 신호의 포락선은 [1]극단을 나타내는 부드러운 곡선입니다.따라서 엔벨로프는 일정한 진폭의 개념을 순간 진폭으로 일반화합니다.그림은 상부 엔벨로프와 하부 엔벨로프 사이에서 변화하는 변조 사인파를 나타냅니다.엔벨로프 함수는 시간, 공간, 각도 또는 실제 변수의 함수일 수 있습니다.
파도 치는 곳에서
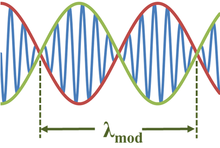
공간 x와 시간 t에서 모두 엔벨로프 함수가 발생하는 일반적인 상황은 파장과 [2]주파수가 거의 같은 두 개의 파형이 중첩되는 것입니다.
는 두 개의 사인파를 더하는 데 삼각 공식을 사용하고 근사치 δ δ λ ≪ λ :
여기서 변조 파장 θ는mod 다음과 [2][3]같이 주어진다.
변조 코사인파의 각 반파장이 변조 사인파의 양의 값과 음의 값을 모두 제어하기 때문에 변조 파장은 엔벨로프 자체의 두 배입니다.마찬가지로 비트 주파수는 엔벨로프의 주파수, 변조파의 2배 또는 2Ωf입니다.[4]
이 파동이 음파라면 f에 관련된 주파수가 귀에 들려 이 소리의 진폭은 비트 [4]주파수에 따라 달라진다.
위상 및 그룹 속도
인자 2'를 제외한 위의 사인파의 인수는 다음과 같습니다.
캐리어와 엔벨로프를 나타내는 첨자 C와 E가 붙어 있습니다.파형의 동일한 진폭 F는 θ와 θ의CE 동일한 값에서 발생하며, 각각 다른 x와 t의 적절한 관련 선택에 대해 동일한 값으로 반환될 수 있습니다.이 불변성은 이러한 파형을 공간에서 추적하여 시간에 따라 전파되는 고정 진폭 위치의 속도를 찾을 수 있음을 의미합니다. 반송파의 인수가 동일하게 유지되는 조건은 다음과 같습니다.
이것은 일정한 진폭을 유지하기 위해 거리 δx는 소위p 위상 속도 v에 의해 시간 간격 δT와 관련이 있음을 보여준다.
한편, 같은 고려사항에 따르면 엔벨로프는 이른바 그룹 속도g v:[5]
그룹 속도에 대한 보다 일반적인 표현은 파동 벡터 k를 도입함으로써 얻을 수 있다.
작은 변화 δ의 경우, 대응하는 파동 벡터의 작은 변화(예를 들어 δk)의 크기는 다음과 같습니다.
따라서 그룹 속도는 다음과 같이 다시 작성할 수 있습니다.
여기서 θ는 라디안/초 단위의 주파수입니다. θ = 2µf입니다.모든 매체에서 주파수와 파동 벡터는 분산 관계인 θ = θ(k)에 의해 관련지어지며, 군 속도는 다음과 같이 쓸 수 있다.

고전적 진공과 같은 매체에서 전자파의 분산 관계는 다음과 같습니다.
여기서0 c는 고전적인 진공상태에서 빛의 속도이다.이 경우 위상 및 그룹 속도는 모두 c입니다0.
이른바 분산매체에서 분산관계는 파동벡터의 복잡한 함수일 수 있으며 위상속도 및 군속도는 동일하지 않다.예를 들어 GaAs의 원자진동(포논)에 의해 나타나는 몇 가지 유형의 파동에 대해 파벡터 k의 다양한 방향에 대한 분산관계를 그림에 나타낸다.일반적인 경우 위상 및 그룹 속도는 방향이 [7]다를 수 있습니다.
함수 근사치
응집물질 물리학에서 결정 내 이동 전하 캐리어의 에너지 고유 함수는 블로흐 파동으로 표현될 수 있습니다.
여기서 n은 밴드(예를 들어 전도 또는 원자가 밴드)의 지수 r은 공간적 위치, k는 파동 벡터입니다.지수는 격자 원자의 코어에 가까운 파동함수의 동작을 기술하는 파동함수n,k u의 빠르게 변화하는 부분을 변조하는 천천히 변화하는 포락선에 대응하는 정현적으로 변화하는 함수이다.엔벨로프는 결정의 Brilouin 구역에 의해 제한된 범위 내의 k-값으로 제한되며, 이는 위치 r에 따라 얼마나 빨리 변할 수 있는지를 제한한다.
양자역학을 이용한 반송파의 거동을 결정할 때, 통상, 슈뢰딩거 방정식이 포락선의 거동만을 참조하도록 간략화된 포락선 근사치를 사용하고, 경계조건을 포락선 [9]함수에 완전한 파동함수가 아닌 직접 적용한다.예를 들어 불순물 근처에 갇힌 반송파의 파동 함수는 블로치 함수의 중첩을 지배하는 엔벨로프 함수 F에 의해 제어된다.
여기서 포락선 F(k)의 푸리에 성분은 대략적인 슈뢰딩거 [10]방정식에서 찾을 수 있다.일부 애플리케이션에서 주기적 부품k u는 밴드 에지 근처의 값(예: k=k0)으로 대체되고, 그 다음:[9]
회절 패턴으로
복수의 슬릿으로부터의 회절 패턴은 단일 슬릿 회절 패턴에 의해 결정되는 엔벨로프를 가진다.단일 슬릿의 경우 패턴은 [11]다음과 같습니다.
여기서 α는 회절각, d는 슬릿폭, θ는 파장이다.여러 슬릿의 경우 패턴은
여기서 q는 슬릿 수이고 g는 격자 상수입니다.첫 번째 요인인 단일 슬릿 결과1 I은 슬릿의 수와 간격에 따라 더 빠르게 변화하는 두 번째 요인을 조절합니다.
견적
디지털 신호 처리에서 엔벨로프는 힐버트 변환 또는 이동 RMS [12]진폭을 사용하여 추정할 수 있다.
「 」를 참조해 주세요.
레퍼런스
- ^ C. Richard Johnson, Jr; William A. Sethares; Andrew G. Klein (2011). "Figure C.1: The envelope of a function outlines its extremes in a smooth manner". Software Receiver Design: Build Your Own Digital Communication System in Five Easy Steps. Cambridge University Press. p. 417. ISBN 978-0521189446.
- ^ a b Blair Kinsman (2002). Wind Waves: Their Generation and Propagation on the Ocean Surface (Reprint of Prentice-Hall 1965 ed.). Courier Dover Publications. p. 186. ISBN 0486495116.
- ^ Mark W. Denny (1993). Air and Water: The Biology and Physics of Life's Media. Princeton University Press. pp. 289. ISBN 0691025185.
- ^ a b Paul Allen Tipler; Gene Mosca (2008). Physics for Scientists and Engineers, Volume 1 (6th ed.). Macmillan. p. 538. ISBN 978-1429201247.
- ^ Peter W. Milonni; Joseph H. Eberly (2010). "§8.3 Group velocity". Laser Physics (2nd ed.). John Wiley & Sons. p. 336. ISBN 978-0470387719.
- ^ Peter Y. Yu; Manuel Cardona (2010). "Fig. 3.2: Phonon dispersion curves in GaAs along high-symmetry axes". Fundamentals of Semiconductors: Physics and Materials Properties (4th ed.). Springer. p. 111. ISBN 978-3642007095.
- ^ V. Cerveny; Vlastislav Červený (2005). "§2.2.9 Relation between the phase and group velocity vectors". Seismic Ray Theory. Cambridge University Press. p. 35. ISBN 0521018226.
- ^ G Bastard; JA Brum; R Ferreira (1991). "Figure 10 in Electronic States in Semiconductor Heterostructures". In Henry Ehrenreich; David Turnbull (eds.). Solid state physics: Semiconductor Heterostructures and Nanostructures. p. 259. ISBN 0126077444.
- ^ a b Christian Schüller (2006). "§2.4.1 Envelope function approximation (EFA)". Inelastic Light Scattering of Semiconductor Nanostructures: Fundamentals And Recent Advances. Springer. p. 22. ISBN 3540365257.
- ^ 예를 들어, 을 참조해 주세요.
- ^ a b Kordt Griepenkerl (2002). "Intensity distribution for diffraction by a slit and Intensity pattern for diffraction by a grating". In John W Harris; Walter Benenson; Horst Stöcker; Holger Lutz (eds.). Handbook of physics. Springer. pp. 306 ff. ISBN 0387952691.
- ^ "Envelope Extraction - MATLAB & Simulink". MathWorks. 2021-09-02. Retrieved 2021-11-16.
이 문서에는 Creative Commons Attribution-ShareAlike 3.0 Unported License에 따라 라이센스가 부여되지만 GFDL에 따라 라이센스가 부여되지 않은 Citizendium 기사 "Envelope function"의 자료가 포함되어 있습니다.
![{\displaystyle {\begin{aligned}F(x,\ t)&=\sin \left[2\pi \left({\frac {x}{\lambda -\Delta \lambda }}-(f+\Delta f)t\right)\right]+\sin \left[2\pi \left({\frac {x}{\lambda +\Delta \lambda }}-(f-\Delta f)t\right)\right]\\[6pt]&\approx 2\cos \left[2\pi \left({\frac {x}{\lambda _{\rm {mod}}}}-\Delta f\ t\right)\right]\ \sin \left[2\pi \left({\frac {x}{\lambda }}-f\ t\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fe1e3d85c2a7bfc6a802ea34e7bd60be82159ed)





















