공간(수학)

수학에서 공간은 어떤 구조가 추가된 집합(때로는 우주라고도 함)이다.

현대 수학은 유클리드 공간, 선형 공간, 위상적 공간, 힐버트 공간, 확률 공간 등 많은 유형의 공간을 사용하지만, '공간' 그 자체에 대한 개념은 정의하지 않는다.^{[1][details 1]}

공간은 점으로 취급되는 선택된 수학적 객체와 이들 점 사이의 선택된 관계로 구성된다. 점의 특성은 매우 다양할 수 있다. 예를 들어 점들은 집합의 요소, 다른 공간의 기능 또는 다른 공간의 하위 공간이 될 수 있다. 공간의 본질을 규정하는 것은 관계다. 더 정확히 말하면, 이소모르퍼스 공간은 동일한 것으로 간주되는데, 여기서 두 공간 사이의 이소모르퍼시픽은 관계를 보존하는 그들의 지점들 사이의 일대일 대응이다. 예를 들어, 3차원 유클리드 공간의 점들 사이의 관계는 유클리드 공리에 의해 독특하게 결정되며,^{[details 2]} 모든 3차원 유클리드 공간은 동일한 것으로 간주된다.

연속성과 같은 위상학적 개념은 모든 유클리드 공간에서 자연적인 정의를 가지고 있다. 그러나 위상은 직선과 곡선을 구분하지 않으며, 유클리드 공간과 위상 공간의 관계는 따라서 "잊혀지는" 것이다. 이러한 종류의 관계는 "공간의 유형" 절에서 더 자세히 다루어진다.

주어진 수학 물체를 기하학적 "공간"으로 고려해야 하는지, 아니면 대수학적 "구조"로 보아야 하는지는 항상 명확하지 않다. 부르바키가 제안한 "구조"의 일반적 정의는 모든 일반적인 유형의 공간을 수용하고,^[2] 이형성에 대한 일반적 정의를 제공하며, 이형 구조들 간의 특성 이전을 정당화한다.

역사

표 1 수학 개념의 역사적 발전

클래식	모던
공리는 정의의 명백한 함축이다.	공리는 상투적이다.
이론은 절대 객관적 진실이다.	이론은 해당 공리의 함축이다.
점, 선 등의 관계는 그 성격에 따라 결정된다.	점, 선 등의 관계는 필수적이다; 그 본성은 그렇지 않다.
수학적인 물체는 그 구조와 함께 우리에게 주어진다.	각각의 수학 이론은 그것의 물체를 그 특성들의 일부에 의해 묘사한다.
기하학은 실험 현실에 해당된다.	기하학은 수학적 진리다.
우주의 모든 기하학적 특성은 공리에서 따온 것이다.	공간의 공리가 모든 기하학적 특성을 결정할 필요는 없다.
기하학은 자율적이고 살아있는 과학이다.	고전 기하학은 수학의 보편적인 언어다.
공간은 입체적이다.	다른 종류의 공간에 다른 차원의 개념이 적용된다.
공간은 기하학의 우주다.	공간은 수학적인 구조일 뿐이고, 그것들은 수학의 다양한 분야에서 발생한다.

기하학의 황금시대 이전

고대 그리스 수학에서 '공간'은 일상생활에서 관찰되는 3차원 현실을 기하학적 추상화시킨 것이다. 기원전 300년경, 유클리드에서는 공간의 속성에 대한 공리를 주었다. 유클리드(Eucleid)는 이러한 기하학적 기초 위에 모든 수학을 구축하여 선 세그먼트의 길이와 선택한 기준 세그먼트의 길이를 비교함으로써 숫자를 정의했다.

좌표법(분석적 기하학)은 1637년 르네 데카르트에 의해 채택되었다.^[3] 당시 기하학적 이론은 직관과 이성을 통해 알 수 있는 절대적 객관적 진리로 취급되었고,^{[4]: 11} 공리는 자연과학의 대상과 유사했으며, 공리는 정의의 명백한 함의로 취급되었다.^{[4]: 15}

기하학적 형상 사이의 등가관계는 일치성과 유사성의 두 가지가 사용되었다. 번역, 회전, 반사는 하나의 형상을 조화로운 형상으로, 동음이의어는 비슷한 형상으로 변형시킨다. 예를 들어, 모든 원은 서로 비슷하지만 타원은 원과 비슷하지 않다. 1795년 Guffard Monge에 의해 소개된 세 번째 등가관계는 투영 기하학에서 발생한다: 타원뿐만 아니라 파라볼라와 하이퍼볼라도 적절한 투영적 변환 하에서 원으로 변한다; 그것들은 모두 투영적으로 동등한 수치들이다.

두 기하학, 유클리드, 투사체 사이의 관계는 수학적 물체가 그 구조로 우리에게 주어지지 않는다는 것을 보여준다.^{[4]: 133 [4]: 21} 오히려, 각각의 수학 이론은 그 이론의 기초에 공리로서 놓여진 것, 정확히 말하면 그 성질의 일부에 의해 그것의 대상을 기술한다.^{[4]: 20}

거리와 각도는 투영 기하학의 공리에는 언급되지도 않고, 투영 기하학의 공리에서는 정의되지도 않기 때문에 투영 기하학의 이론에는 나타날 수 없다. "삼각형의 세 각의 합은 무엇인가"라는 질문은 유클리드 기하학에서는 의미가 있지만 투영 기하학에서는 의미가 없다.

19세기에는 다른 상황이 나타났다: 어떤 기하학에서는 삼각형의 세 각의 합이 잘 정의되어 있으나 고전적 가치(180도)와는 다르다. 1829년 니콜라이 로바체프스키와 1832년 야노스 볼야이에 의해 소개된 비유클리드 쌍곡 기하학(그리고 1816년, 미발표)^{[4]: 133} 은 이 합계는 삼각형에 따라 달라지며 항상 180도 미만이라고 명시했다. 1868년 유제니오 벨트라미, 1871년 펠릭스 클라인이 비유클리드 쌍곡 기하학의 유클리드 "모듈"을 입수하여 이 이론을 논리적인 가능성으로 완전히 정당화하였다.^{[4]: 24 [5]}

이 발견은 유클리드 기하학의 절대적 진리에 대한 가식을 포기하도록 강요했다. 그것은 공리가 "명확한" 것도 아니고 "정의의 암시"도 아니라는 것을 보여주었다. 오히려 가설이다. 그들은 어느 정도까지 실험적인 현실에 대응하고 있는가? 이 중요한 신체적 문제는 더 이상 수학과는 관계가 없다. "지오메트리"가 실험 현실과 일치하지 않더라도, 그 이론은 "수학적 진실"^{[4]: 15} 에 못지 않게 남아 있다.

비유클리드 기하학의 유클리드 모델은 유클리드 공간에 존재하는 일부 물체와 비유클리드 기하학의 모든 공리(따라서 모든 이론)를 만족시키는 이들 물체들 사이의 어떤 관계를 선택하는 것이다. 이러한 유클리드 사물과 관계는 고대 공연을 하는 현대 배우들처럼 유클리드 이외의 기하학을 "연극"한다. 배우들은 현실에서 결코 일어나지 않았던 상황을 흉내낼 수 있다. 무대에 오른 배우들의 관계는 극중 인물들 간의 관계를 모방한다. 마찬가지로 유클리드 모델의 선택된 대상들 사이의 선택된 관계는 유클리드 이외의 관계를 모방한다. 수학에서는 사물 간의 관계가 필수적인 반면, 사물의 본질은 그렇지 않다는 것을 보여준다.

황금시대 이후

"지오메트리"(고대 그리스어: 지오-지구 "지구", -메트론 "측정")라는 단어는 처음에 우리가 살고 있는 공간에서 길이, 지역, 부피를 처리하는 실용적인 방법을 의미했지만, 그 다음에는 광범위하게 확장되었다(여기 문제의 공간에 대한 개념도 여기에 있다).

부르바키에 따르면 1795년(몽게를 묘사한 게오메트리)에서 1872년(클라인의 에를랑겐 프로그램) 사이의 기간은 기하학의 황금시대라고 할 수 있다.^{[4]: 131} 유클리드(Eucleid)가 조사한 원래 공간을 이제는 입체 유클리드(Eucleidian) 공간이라고 부른다. 23세기 전 유클리드(유클리드)에 의해 시작된 그것의 공리화는 힐베르트의 공리, 타르스키의 공리, 비르코프의 공리로 개혁되었다. 이러한 공리 시스템은 여러 공리에 의해 제약된 원시 개념(예: "점", "간", "합치")을 통해 공간을 설명한다.

분석적 기하학은 큰 진전을 이루었고 변환 그룹의 불변수를 통한 계산으로 고전적 기하학의 이론들을 대체하는데 성공했다.^{[4]: 134, 5} 그 이후로 고전 기하학의 새로운 이론들은 전문 수학자들보다는 아마추어들에게 더 많은 관심을 가져왔다.^{[4]: 136} 그러나 고전 기하학의 유산은 잃지 않았다. 부르바키에 따르면,^{[4]: 138} "자율적이고 살아있는 과학으로서의 역할을 거쳐, 고전적 기하학은 따라서 현대 수학의 보편적인 언어로 변모된다"고 한다.

동시에, 숫자는 기하학을 수학의 기초로서 대체하기 시작했다. 예를 들어, 리처드 드데킨드의 1872년 에세이 Stetigkeit und 비이성적인 Zahlen(지속성과 비이성적인 숫자)에서, 그는 선 위의 점들이 데데킨드의 특성을 잘라야 하며, 따라서 선은 실수의 집합과 같은 것이라고 주장한다. 디데킨드는 이것이 증명될 수 없는 가정이라는 것을 주의 깊게 알아차린다. 현대 치료에서 데데킨드의 주장은 흔히 선의 정의로 받아들여져 기하학을 산술로 축소시킨다. 3차원 유클리드 공간은 원소 차이의 관련 벡터 공간이 내부 생산물을 갖추고 있는 아핀 공간으로 정의된다.^[6] 유클리드처럼 "원래부터"라는 정의는 이 공간과 다른 공간의 관계를 드러내지 않기 때문에 이제는 자주 사용되지 않는다. 또한, 3차원 투영 공간은 이제 4차원 벡터 공간의 모든 1차원 서브 스페이스(즉, 원점을 통과하는 직선)의 공간으로 정의된다. 이러한 기초의 변화에는 새로운 공리가 필요하며, 이러한 공리가 채택되면 기하학의 고전적 공리는 이론이 된다.

현재 공간은 점으로 취급되는 선택된 수학적 객체(예를 들어 다른 공간의 함수 또는 다른 공간의 서브 스페이스 또는 단지 집합의 요소)와 이들 점 사이의 선택된 관계로 구성되어 있다. 그러므로 공간은 편의의 수학적인 구조일 뿐이다. 「공간」이라고 하는 구조가 다른 수학적 물체보다 기하학적으로 인식되는 것을 기대할 수도 있지만, 이것이 항상 사실인 것은 아니다.

1854년 베른하르트 리만(Bernhard Riemann)의 유명한 취임식 강연에 따르면, n개의 실제 숫자로 파라메트리가 된 모든 수학적인 물체는 그러한 모든 물체의 n차원 공간의 한 점으로 취급될 수 있다.^{[4]: 140} 현대의 수학자들은 이 생각을 일상적으로 따르고 거의 모든 곳에서 고전 기하학의 용어를 사용하는 것이 매우 시사적이라고 생각한다.^{[4]: 138}

함수는 중요한 수학 물체다. 대개 리만이^{[4]: 141} 이미 지적하고 20세기에 기능분석에 의해 정교하게 기술한 것처럼 무한차원 기능공간을 형성한다.

공간 분류법

분류법 3계급

각 유형의 공간은 고유한 정의를 가지고 있지만, "공간"에 대한 일반적인 생각은 형식화를 회피한다. 어떤 구조물들은 공간이라고 불리고, 다른 구조물들은 그렇지 않다, 형식적인 기준이 없다. 게다가, "구조"라는 일반적인 생각에 대한 공감대가 형성되어 있지 않다. Pudlahk에 따르면,^[7] "수학 [...]은 수학 구조와 같은 하나의 개념으로 완전히 설명될 수 없다. 그럼에도 부르바키의 구조주의적 접근은 우리가 가진 것 중 최고다." 우리는 마지막 절 "공간과 구조물"에서 부르바키의 구조주의적 접근방식으로 되돌아갈 것이며, 이제 부르바키 정신에서 가능한 공간(및 구조물)의 분류에 대해 개략적으로 설명할 것이다.

우리는 공간을 세 단계로 분류한다. 각각의 수학 이론이 그것의 물체를 그들의 특성들 중 일부에 의해 설명한다는 것을 고려하면, 첫번째 질문은: 어떤 특성들인가?이다. 이는 첫 번째(상단) 분류 단계로 이어진다. 2단계에서는 특히 중요한 질문에 대한 답을 고려한다(1단계에 따라 말이 되는 질문 중). 3단계 분류에서는 가능한 모든 질문에 대한 답을 고려한다.

예를 들어, 두 점 사이의 거리는 유클리드 공간에서는 정의되지만 투영 공간에서는 정의되지 않기 때문에 상위 수준 분류는 유클리드 공간과 투영 공간을 구분한다. 또 다른 예. "삼각형의 세 각의 합은 무엇인가"라는 질문은 유클리드 공간에서는 이해가 되지만 투영 공간에서는 그렇지 않다. 유클리드 이외의 공간에서는 그 질문이 타당하지만 다르게 대답되는데, 이것은 상위 수준의 구분이 아니다.

또한 유클리드 평면과 유클리드 3차원 공간의 구분이 상위 수준의 구분이 아니며, "차원이 무엇인가"라는 질문도 두 경우 모두 일리가 있다.

2차 분류는 예를 들어 유클리드 공간과 비유클리드 공간, 유한 차원 공간과 무한 차원 공간, 소형 공간과 비복합 공간 등을 구분한다. 부르바키의 용어로 ^[2]2차 분류는 "종"에 의한 분류다. 생물 분류학과는 달리, 공간은 여러 종에 속할 수 있다.

3차원의 분류는 예를 들어 차원이 다른 공간을 구분하지만, 2차원 유클리드 공간으로 취급되는 3차원 유클리드 공간의 평면과 모든 실수의 집합도 구별하지 않으며, 또한 2차원 유클리드 공간으로 취급된다. 마찬가지로 동일한 비유클리드 공간의 서로 다른 유클리드 모델을 구별하지 않는다. 좀 더 형식적으로, 3단계는 공간을 이등형성으로 분류한다. 두 공간 사이의 이형성(異形性)은 제1공간의 지점과 제2공간의 지점 사이의 일대일 대응으로 정의되며, 제1공간에 따라 규정된 모든 관계를 보존한다. 상호 이형 공간은 단일 공간의 복사라고 생각된다. 만약 그들 중 한 명이 주어진 종에 속한다면, 그들은 모두 그렇게 한다.

이형사상이라는 개념은 상위 등급 분류를 조명한다. 같은 상위 계층의 두 공간 사이에 일대일 서신 왕래를 할 경우, 그것이 이형인지 아닌지를 물을 수도 있다. 이 질문은 서로 다른 계층의 두 공간에 대해 말이 되지 않는다.

그 자체에 대한 이형성을 자동형성이라고 한다. 유클리드 공간의 자동형은 이것들의 이동, 회전, 반사, 구성이다. 유클리드 공간은 모든 포인트가 어떤 오토모프리즘에 의해 다른 모든 포인트로 변형될 수 있다는 점에서 동질적이다.

유클리드 공리는^{[details 2]} 자유를 남기지 않는다; 그것들은 우주의 모든 기하학적 특성을 독특하게 결정한다. 더 정확히 말하자면, 모든 3차원 유클리드 공간은 상호 이형성이다. 이런 의미에서 우리는 "3차원" 유클리드 공간을 가지고 있다. 부르바키의 용어로 보면 그에 상응하는 이론은 일률적이다. 이와는 대조적으로 위상학적 공간은 일반적으로 이질성이 없다; 그들의 이론은 다원적이다. 수학적 논리학에서도 비슷한 생각이 일어난다: 동일한 카디널리티의 모든 모델이 상호 이형성이라면 이론은 범주형이라고 불린다. 부르바키에 따르면 ^[8]다원적 이론에 대한 연구는 현대 수학과 고전 수학을 구분하는 가장 두드러진 특징이다.

공간종간의 관계

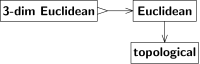
위상학적 개념(연속성, 수렴성, 오픈 세트, 폐쇄 세트 등)은 모든 유클리드 공간에서 자연스럽게 정의된다. 즉 모든 유클리드 공간도 위상학적 공간이다. 두 유클리드 공간 사이의 모든 이형성 역시 해당 위상학적 공간 사이의 이형성('동형성'이라고 불림)이지만, 그 반대는 틀렸다:동형성이 거리를 왜곡할 수도 있다. 부르바키의 용어로 '위상 공간'은 ^[2]'유클리드 공간' 구조의 밑바탕이 되는 구조다. 카테고리 이론에서도 유사한 생각이 발생한다: 유클리드 공간의 카테고리는 위상학적 공간의 카테고리에 대한 구체적인 카테고리; 건망증(또는 "스트립핑") 펑터(functor)는 전자 카테고리를 후자의 카테고리에 매핑한다.

3차원 유클리드 공간은 유클리드 공간의 특별한 경우다. 부르바키의 용어로 3차원 유클리드 공간의 종은 유클리드 공간의 종보다 풍부하다.^[2] 마찬가지로, 콤팩트한 위상 공간의 종은 위상 공간의 종보다 풍부하다.

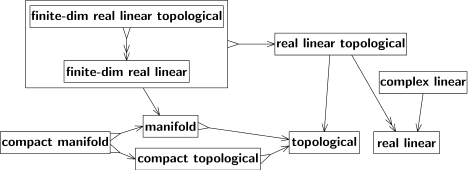
공간의 종들 간의 그러한 관계는 그림 3에 나타낸 것과 같이 도식적으로 표현될 수 있다. A에서 B까지의 화살표는 모든 A-공간도 B-공간이거나 B-공간으로 취급될 수 있거나 B-공간 등을 제공하는 것을 의미한다. A와 B를 공간의 종류로 취급하는 것은 화살을 A에서 B로 전환하는 것으로 해석할 수 있다(Bourbaki의 용어에서 ^[9]A-공간에서 B-공간을 "공제 절차"). 클래스 A,B가 설정되지 않는 한 그다지 중요한 함수는 아니다. 이러한 뉘앙스가 다음을 무효화하지 않는다.) 그림 3의 두 개의 화살은 변환할 수 없는 것이 아니라 서로 다른 이유로 되어 있다.

"유클리드"에서 "토폴로지"로의 전환은 건망증이 심하다. 위상은 연속성과 불연속성을 구별하지만 직선성과 곡선성을 구분하지 않는다. 직관은 유클리드 구조는 위상에서 회복될 수 없다는 것을 말해준다. 증명에는 위상학적 공간(즉, 자기 동형)의 자동형성(즉, 이동, 회전, 반사의 구성이 아닌 자기 동형성)이 사용된다. 그러한 변형은 주어진 유클리드 구조를 (이형성적이지만) 다른 유클리드 구조로 변화시킨다. 두 유클리드 구조는 모두 단일 위상학적 구조에 해당한다.

이와는 대조적으로, 「3차원 유클리드」에서 「유클리드」로 이행하는 것은 건망증이 있는 것이 아니다; 유클리드 공간은 3차원일 필요는 없지만, 우연히 3차원이라면, 완전하게 되어, 어떤 구조도 없어진다. 즉 후자의 전환은 주입식(일대일)인 반면, 전자의 전환은 주입식(다대일)이 아니다. 우리는 "→"가 아닌 "↣"라는 철조망을 가진 화살에 의한 주입 전환을 나타낸다.

두 전환 모두 허탈하지 않으며, 즉 모든 B-공간이 일부 A-공간에서 발생하는 것은 아니다. 첫째, 3차원 유클리드 공간은 유클리드 공간의 특별한 (일반적이지 않은) 경우다. 둘째, 유클리드 공간의 위상은 위상의 특별한 경우다(예를 들어, 비 컴팩트적, 연결적이어야 한다 등). 우리는 "→"가 아닌 "↠"라는 두 개의 머리 화살표로 비참한 전환을 나타낸다. 그림 4를 참조하십시오. 여기서 "실제 선형 위상학"에서 "실제 선형"까지의 화살표는 두 개의 머리 모양이며, 모든 실제 선형 공간은 선형 구조와 호환되는 일부(최소한 하나) 위상을 허용하기 때문이다.

이러한 위상은 일반적으로 고유하지 않지만 실제 선형 공간이 유한한 경우 고유하다. 이러한 공간의 경우 전환은 주입적 및 허탈적, 즉 비주사적이다. 그림 4의 "완료-딤 실제 선형 위상학"에서 "완료-딤 실제 선형"까지의 화살표를 참조한다. 역전이 존재하며(두 번째 역방향 화살표로 표시될 수 있음) 따라서 두 종류의 구조물은 동등하다. 실제로, 사람들은 동등한 종류의 구조물을 구별하지 않는다.^[10] 등가 구조물은 그림 4의 큰 상자에 표시된 것처럼 단일 구조물로 취급할 수 있다.

화살표가 나타내는 전환은 이형성에 따른다. 즉, 두 개의 이형성 A-공간은 두 개의 이형성 B-공간으로 이어진다.

그림 4의 도표는 서로 상응한다. 즉, 시작과 끝점이 같은 다이어그램의 모든 방향 경로가 동일한 결과를 초래한다. 그림 9의 점선 화살을 제외하고 아래의 다른 도표들도 대응적이다. "위상학"에서 "측정이 가능한"까지의 화살표는 거기서 설명되는 이유 때문에 파쇄된다. "위상학적 공간을 측정 가능한 공간으로 바꾸기 위해서는 σ-알제브라( end-algebra)로 지탱한다. 보렐 세트의 σ-알제브라 세트가 가장 인기 있지만 유일한 선택은 아니다." 고체 화살표는 자신을 자연스럽게 암시하고 종종 암묵적으로 광범위하게 사용되고 있는 이른바 "캐논적" 전환을 의미한다. 예를 들어, 유클리드 공간의 연속 함수에 대해 말하자면, 위상은 명시적으로 지정할 필요가 없다. 사실, 대체 위상은 존재하며, 예를 들어, 미세 위상과 같은 경우에 사용되기도 하지만, 이러한 위상은 일반적인 위상에 비해 훨씬 덜 눈에 띄기 때문에 항상 명시적으로 지정된다. 점선 화살표는 여러 전환이 사용 중이고 어느 누구도 널리 보급되지 않음을 나타낸다.

공간 유형

선형 및 위상 공간

두 개의 기본공간은 선형공간(벡터공간이라고도 함)과 위상공간이다.

선형 공간은 대수적 성격을 띤다; 실제 선형 공간(실수 영역 위에), 복잡한 선형 공간(복잡한 숫자 영역 위에), 그리고 더 일반적으로 어떤 영역에도 선형 공간이 있다. 모든 복잡한 선형 공간은 또한 실제 선형 공간이다(후자는 전자의 기초가 된다). 각각의 실제 숫자는 또한 복잡한 숫자이기 때문이다.^{[details 3]} 보다 일반적으로, 필드 위의 벡터 공간은 또한 그 필드의 하위 필드 위에 벡터 공간의 구조를 가지고 있다. 선형 연산은 정의에 의해 선형 공간에 주어지며 직선(및 평면 및 기타 선형 하위 공간), 평행선, 타원(및 타원)과 같은 개념으로 이어진다. 그러나 직교(수직)선을 정의하거나 타원 사이에 원을 하나 내는 것은 불가능하다. 왜냐하면 선형 공간에는 각도를 측정하는 데 사용될 수 있는 스칼라 제품과 같은 구조가 없기 때문이다. 선형 공간의 치수는 선형 독립 벡터의 최대 수로 정의되며, 동등하게 공간에 걸쳐 있는 최소 벡터 수로 정의된다. 유한하거나 무한할 수 있다. 동일한 필드 위에 있는 두 개의 선형 공간은 동일한 차원일 경우에만 이형이다. n차원 복합 선형 공간도 2n차원 실제 선형 공간이다.

위상학적 공간은 분석적 성격을 띤다. 정의에 의해 위상학적 공간에 주어진 오픈 세트는 연속적인 기능, 경로, 지도, 수렴 순서, 한계, 내부, 경계, 외부와 같은 개념으로 이어진다. 그러나, 균일한 연속성, 경계 집합, Cauchy 시퀀스, 구별 가능한 함수(경로, 맵)는 정의되지 않은 상태로 남아 있다. 위상학적 공간 사이의 이소모르프리즘은 전통적으로 동형상이라고 불린다. 이것들은 양방향으로 연속되는 일대일 대응이다. 개방 간격(0,1)은 전체 실선에 대해 동형이지만 폐쇄 간격[0,1]에 대해서는 동형형이 아니며 원에도 동일하지 않다. 정육면체의 표면은 구체(공 표면)에 대해서는 동형이지만 토러스에는 동형형이 아니다. 차원이 다른 유클리드 공간은 분명해 보이지만 증명하기가 쉽지 않은 동형체다. 위상학적 공간의 치수는 정의하기 어렵다. 귀납적 치수(기하학적 도형의 경계 치수가 보통 도형의 치수보다 1이 적다는 관찰에 근거함)와 치수를 덮는 르베그(Lebesgue)를 사용할 수 있다. n차원 유클리드 공간의 경우 두 위상학적 치수는 모두 n과 같다.

위상학적 공간의 모든 부분 집합은 그 자체로 위상학적 공간이다(대조적으로, 선형 공간의 선형 부분 집합만 선형 공간이다). 일반 위상(포인트 집합 위상이라고도 함)에 의해 조사된 임의 위상 공간은 동형상까지 완전한 분류를 하기에는 너무 다양하다. 콤팩트한 위상학적 공간은 위상학적 공간의 중요한 분류("종류")이다. 모든 연속적인 기능은 그러한 공간에 한정되어 있다. 닫힌 간격[0,1]과 확장된 실선[-line,line]은 콤팩트하며, 개방 간격(0,1)과 라인(-line,line)은 콤팩트하지 않다. 기하학적 위상은 다지관을 조사한다(이 "형"의 또 다른 "종"). 이것들은 유클리드 공간에 대한 국소적 동형상 공간이다(그리고 몇 가지 추가 조건을 만족한다). 저차원 다지관은 완전히 동형상까지 분류된다.

선형 구조와 위상 구조 모두 선형 위상 공간(즉, 위상 벡터 공간) 구조의 기초가 된다. 선형 위상 공간은 실제 또는 복잡한 선형 공간이며, 선형 연산이 연속적으로 이루어지는 위상 공간이다. 따라서 위상학적 공간도 일반적으로 선형 위상학적 공간은 아니다.

모든 유한차원 실질 또는 복합 선형 공간은 하나의 위상만을 운반한다는 의미에서 선형 위상 공간으로서 선형 위상 공간이다. 따라서 두 구조인 "완료 차원 실제 또는 복합 선형 공간"과 "완료 차원 선형 위상 공간"은 상호 기반이 동일한 것이다. 이에 따라 유한차원 선형 위상학적 공간의 모든 반전성 선형 변환은 동형상이다. 차원(대수학 1개, 위상학 2개)의 3개 개념은 유한차원 실제 선형 공간에 대해 일치한다. 그러나 무한 차원 공간에서는 다른 위상이 주어진 선형 구조에 부합할 수 있으며, 반전 가능한 선형 변환은 일반적으로 동형성이 아니다.

아핀 및 투영 공간

선형공간에 의한 아핀·프로젝티브공간의 도입은 다음과 같이 편리하다. n차원 선형공간인 a (n+1)차원 선형공간은 그 자체가 n차원 선형공간인 n차원 선형공간이 동질적이지 않고, 원점인 특별한 점을 포함하고 있다. 그것을 외부의 벡터로 이동시키면, n차원 아핀 하위 공간을 얻는다. 균질하다. 아핀 공간은 선형 공간에 포함될 필요가 없지만, 선형 공간의 아핀 하위 공간에는 이형성이 있다. 모든 n차원 아핀 공간은 상호 이형이다. John Baez의 말에 따르면, "접착 공간은 그 기원을 잊은 벡터 공간이다." 특히 모든 선형 공간은 아핀 공간이기도 하다.

a (n+1)차원 선형 공간 L에서 n차원 아핀 아공간 A를 주어진다면, A의 직선은 A:를 교차하는 L의 2차원 선형 아공간을 가진 A의 교차점, 즉 A와 평행하지 않은 원점을 통과하는 평면으로 정의할 수 있다. 보다 일반적으로 A의 k-차원 아핀 하위공간은 A를 교차하는 L의 (k+1)차원 선형 아공간과 A의 교차점이다.

아핀 하위공간 A의 모든 점은 1차원 선형 하위공간 L과 A의 교차점이다. 그러나 L의 일부 1차원 서브스페이스는 A와 평행하며, 어떤 의미에서는 무한에서 A와 교차한다. a (n+1)차원 선형 공간의 모든 1차원 선형 하위공간 집합은 정의상 n차원 투영공간이다. 그리고 아핀 하위 공간 A는 적절한 부분집합으로서 투영 공간에 내장되어 있다. 그러나 투영 공간 자체가 동질적이다. 투사 공간의 직선은 (n+1)차원 선형 공간의 2차원 선형 하위 공간에 해당한다. 보다 일반적으로 투사 공간의 k차원 투사적 아공간은 (n+1)차원 선형 공간의 (k+1)차원 선형 아공간과 일치하며, k차원 투사공간과 이형성이 있다.

이런 식으로 정의하면, 아핀과 투영 공간은 대수학적 성질의 것이다; 그것들은 어떤 분야에 걸쳐도 실제적이고, 복잡하며, 보다 일반적일 수 있다.

모든 실제적이거나 복잡한 애프틴이나 투영적인 공간도 위상학적 공간이다. 아핀 공간은 비 컴팩트 다지관이고 투영 공간은 콤팩트 다지관이다. 실제 투영 공간에서는 직선이 원과 동질적이므로 아핀 공간의 선형에서 직선과 대조적으로 콤팩트하다.

미터법 및 균일한 공간

점 사이의 거리는 미터법 공간에서 정의된다. 미터법 공간 사이의 이소모형을 이소메트리라고 한다. 모든 미터법 공간은 위상학적 공간이기도 하다. 위상학적 공간은 미터법 공간의 기초가 되는 경우 메트리저블(metrizable은 미터법 공간의 기초가 된다. 모든 다지관은 측정이 가능하다.

미터법 공간에서는 경계 집합과 카우치 시퀀스를 정의할 수 있다. 모든 Cauchy 시퀀스가 수렴하면 미터법 공간을 complete라고 부른다. 모든 불완전한 공간은 밀집된 부분 집합으로서 완전한 공간(완성)에 등축적으로 내장된다. 모든 소형 메트릭스 공간이 완료됨; 실제 라인은 비소형이지만 완전함, 열린 간격(0,1)은 불완전함.

모든 유클리드 공간도 완전한 미터 공간이다. 게다가, 유클리드 공간에 내재하는 모든 기하학적 개념은 그 미터법으로 특징지어질 수 있다. 예를 들어, 주어진 두 점 A와 C를 연결하는 직선 세그먼트는 A와 C 사이의 거리가 A와 B 사이, B와 C 사이의 두 거리의 합계와 같도록 모든 점 B로 구성된다.

하우스도르프 차원(주어진 세트를 커버하는 작은 볼의 수와 관련됨)은 미터법 공간에 적용되며, 비인정자(특히 프랙탈의 경우)가 될 수 있다. n차원 유클리드 공간의 경우 하우스도르프 치수는 n과 같다.

균일한 공간은 거리를 도입하지 않지만, 여전히 균일한 연속성, Cauchy 시퀀스(또는 필터나 그물), 완전성과 완성도를 사용할 수 있다. 모든 균일한 공간은 위상학적 공간이기도 하다. 모든 선형 위상학적 공간(메트리징 가능 여부)도 균일한 공간이며, 유한한 차원에서는 완전하지만 무한 차원에서는 일반적으로 불완전하다. 더 일반적으로, 모든 상호 작용 위상학 그룹은 균일한 공간이다. 그러나 비확정적 위상학 집단은 두 개의 균일한 구조물을 운반하는데, 하나는 좌상변동체, 다른 하나는 우상변동체다.

노르메드, 바나흐, 내부 제품 및 힐버트 공간

유클리드 공간의 벡터는 선형 공간을 형성하지만, 각 $벡터{\displaystyle }$ x ${\displaystyle$ x$}$도 길이, 즉${\displaystyle }$other x${\displaystyle }$‖ ${\displaystyle \lVert x\rVert }.$ 규범과 함께$$ 부여된 실제 또는 복잡한 선형 공간은 규범된 공간이다$.$ 모든 표준 공간은 선형 위상학적 공간과 미터법 공간이다. 바나흐 공간은 완전히 규범화된 공간이다. 시퀀스나 함수의 많은 공간은 무한한 차원의 바나흐 공간이다.

표준 벡터가 1보다 작은 모든 벡터를 표준 공간의 단위 공이라고 한다. 이것은 볼록한 중심 대칭 집합이며, 일반적으로 타원체가 아니다. 예를 들어, 그것은 (평면에서) 다각형일 수도 있고, 더 일반적으로 (임의의 유한 치수에서) 폴리토프일 수도 있다. 평행사변형법(평행사변형 ID라고도 함)

${\displaystyle \lVert x-y\rVert ^{2}+\lVert x+y\rVert ^{2}=2\lVert x\rVert ^{2}+2\lVert y\rVert ^{2}\rVert ^{2}\rVert }\,}$

일반적으로 규범화된 공간에서는 실패하지만, 유클리드 공간에서는 벡터를 보유하는데, 이는 벡터의 제곱 유클리드 규범이 그 자체로 내부 제품이라는 사실에서 따온 것으로서, $\Vert {\displaystyle }$ ${\displaystyle x}$ ${\displaystyle {2\mathrm{}}^{}}$=${\displaystyle }$( ${\displaystyle x}$, ${\displaystyle x}$) ${\displaystyle \lVert$x$\rVert$^{$2}=(x,$x$)\}.$

내부 제품 공간은 실제적이거나 복잡한 선형 공간이며, 이선형 또는 각 선형의 형태를 부여하여 일부 조건을 만족하고 내부 제품이라고 불린다. 모든 내부 제품 공간도 규범화된 공간이다. 표준화된 공간은 병렬로그램 법칙을 만족하는 경우에만 내부 제품 공간의 기초가 되며, 단위 볼이 타원형인 경우에도 동등하게 적용된다. 벡터 사이의 각도는 내부 제품 공간에서 정의된다. 힐버트 공간은 완전한 내부 제품 공간으로 정의된다. (어떤 저자들은 그것이 복잡해야 한다고 주장하기도 하고, 다른 저자들은 실제 힐버트 공간을 인정하기도 한다. 시퀀스나 함수의 많은 공간은 무한한 차원의 힐버트 공간이다. 힐버트 공간은 양자 이론에 매우 중요하다.^[11]

모든 n차원 실제 내부 제품 공간은 상호 이형이다. N차원 유클리드 공간은 그 기원을 잊은 n차원 실제 내제품 공간이라고 말할 수도 있다.

매끈하고 리만적인 다지관

매끄러운 다지관은 "공간"이라고 불리지 않지만, 그럴 수도 있다. 모든 매끄러운 다지관은 위상학적 다지관이며, 유한차원 선형 공간에 삽입될 수 있다. 유한차원 선형 공간의 매끄러운 표면은 매끄러운 다지관이다. 예를 들어 타원체의 표면은 매끄러운 다지관이고, 폴리토프는 그렇지 않다. 실제 또는 복합적인 유한차원 선형, 아핀 및 투영 공간도 매끄러운 다지관이다.

그것의 각 지점에서, 매끄러운 다지관의 부드러운 경로에는 이 지점에서 다지관의 접선 공간에 속하는 접선 벡터가 있다. n차원 매끄러운 다지관의 접선 공간은 n차원 선형 공간이다. 매끄러운 다지관의 매끄러운 기능의 차이는 각 지점의 접선 공간에 선형 기능을 제공한다.

리만 다지관, 즉 리만 공간은 부드러운 다지관으로, 접선 공간은 어떤 조건을 만족하는 내부 제품을 가지고 있다. 유클리드 공간도 리만 공간이다. 유클리드 공간의 매끄러운 표면은 리만 공간이다. 쌍곡선 비유클리드 공간도 리만 공간이다. 리만 공간의 곡선은 길이를 가지며, 두 점 사이의 최단 곡선의 길이는 거리를 규정하여 리만 공간이 미터법 공간이다. 한 점에서 교차하는 두 곡선 사이의 각도는 접선 사이의 각이다.

접선 공간에서 내부 제품의 긍정을 포기하면 일반 상대성에 매우 중요한 로렌츠 공간을 포함한 유사-리만 공간을 얻는다.

측정 가능, 측정 및 확률 공간

(기하학적 신체의) 체적을 유지하면서 거리와 각도를 내리는 것은 측정 이론에 도달한다. 안드레이 콜모고로프의 확률 이론에 대한 접근방법에 따라 볼륨 외에 면적, 길이, 질량(또는 전하) 분포, 확률 분포의 개념도 일반화한다.

고전 수학의 "기하학 본체"는 단순한 점 집합보다 훨씬 더 규칙적이다. 신체의 경계는 부피가 0이다. 따라서 신체의 부피는 그 내부의 부피로 되어 있으며, 내부는 무한히 연속된 큐브에 의해 소진될 수 있다. 이와는 대조적으로 임의의 점 집합의 경계는 0이 아닐 수 있다(예: 주어진 큐브 내의 모든 합리적 점 집합). 측정 이론은 볼륨의 개념을 방대한 종류의 집합, 이른바 측정 가능한 집합으로 확장하는 데 성공했다. 실제로 측정 불가능한 집합은 애플리케이션에서 거의 발생하지 않는다.

측정 가능한 세트는 정의에 따라 측정 가능한 공간에 주어지며, 측정 가능한 기능과 지도로 이어진다. 위상학적 공간을 측정 가능한 공간으로 바꾸기 위해 σ-알지브라(al-algebra)를 붙인다. 보렐 세트의 σ-algebra는 가장 인기 있지만 유일한 선택은 아니다. (배어 세트, 보편적으로 측정할 수 있는 세트 등도 가끔 사용된다.) 위상은 보렐 σ-알지브라에 의해 고유하게 결정되지 않는다. 예를 들어, 분리 가능한 힐버트 공간의 표준 위상과 약한 위상은 동일한 보렐 al-알지브라로 이어진다. 모든 σ-algebra가 어떤 위상의 보렐 σ-algebra는 아니다.^{[details 4]} 실제로 σ-알지브라는 어떤 위상에 관계 없이 주어진 집합(또는 함수)에 의해 생성될 수 있다. 측정 가능한 공간의 모든 부분 집합은 그 자체로 측정 가능한 공간이다.

표준 측정 가능한 공간(표준 보렐 공간이라고도 함)은 콤팩트한 공간과 어느 정도 유사하기 때문에 특히 유용하다(EoM 참조). 표준 측정 가능한 공간 사이의 모든 생체 측정 가능한 지도는 이소모르프다. 즉, 역 지도 역시 측정할 수 있다. 그리고 그러한 공간 간의 매핑은 제품 공간에서 그래프를 측정할 수 있는 경우에만 측정할 수 있다. 마찬가지로, 콤팩트한 미터법 공간 사이의 모든 생체적 연속 매핑은 동형상이다. 즉, 역방향 매핑 역시 연속적이다. 그리고 그러한 공간 간의 매핑은 제품 공간에서 해당 그래프가 닫힌 경우에만 연속적이다.

보렐 σ-알게브라가 부여한 유클리드 공간(그리고 더 일반적으로는 완전 분리 가능한 미터 공간)에 설정된 모든 보렐은 표준 측정 가능한 공간이다. 계산할 수 없는 모든 표준 측정 가능 공간은 상호 이형이다.

측정 공간은 측정이 부여된 측정 가능한 공간이다. 르베그 측도가 있는 유클리드 공간은 측정 공간이다. 통합 이론은 측정 공간에서의 측정 가능한 기능의 통합성과 통합을 정의한다.

null 집합이라고 하는 측정값 0 집합은 무시할 수 있다. 따라서 "mod 0 이형성"은 완전 측정(즉, 무시할 수 있는 보완성을 가진) 하위 집합 사이의 이형성으로 정의된다.

확률공간은 전체 공간의 측정이 1과 같은 측정공간이다. 확률 공간의 모든 패밀리(마인트가 되든 안 되든)의 산출물은 확률 공간이다. 대조적으로, 일반적으로 측정 공간의 경우, 미세하게 많은 공간의 곱만이 정의된다. 이에 따라 무한 차원 확률 측정(특히 가우스 측도)은 많지만, 무한 차원 르베그 측도는 없다.

표준 확률 공간은 특히 유용하다. 표준 확률 공간에서는 조건부 기대치를 조건부 측정치(정규 조건부 확률, 측정치 분해 참조)에 대한 적분으로 취급할 수 있다. 두 개의 표준 확률 공간이 주어지면, 그들의 측정 알헤브라의 모든 동형성은 지도를 보존하는 어떤 측정에 의해 유도된다. 표준 측정 가능한 공간에 대한 모든 확률 측정은 표준 확률 공간으로 이어진다. 표준 확률 공간의 시퀀스(마감이 되든 안 되든)의 산출물은 표준 확률 공간이다. 모든 비원자 표준 확률 공간은 상호 이형모드 0이며, 그 중 하나는 르베그 측정이 있는 구간(0,1)이다.

이 공간들은 덜 기하학적인 것이다. 특히 치수의 개념은 (하나의 형태나 다른 형태로) 다른 모든 공간에 적용할 수 있으며, 측정 가능 공간, 측정 공간 및 확률 공간에는 적용되지 않는다.

비확정 기하학

수학적 분석으로 알려진 미적분학의 이론적 연구는 20세기 초 실제 가치 함수나 복합 가치 함수의 선형 공간에 대한 고려로 이어졌다. 이것들의 초기 예들은 기능 공간이었는데, 각각은 그들만의 문제 종류에 맞게 조정되었다. 이러한 예들은 많은 공통적인 특징들을 공유했고, 이러한 특징들은 곧 힐버트 공간, 바나흐 공간, 그리고 보다 일반적인 위상학적 벡터 공간으로 추상화되었다. 이것들은 광범위한 수학 문제를 해결하기 위한 강력한 도구 키트였다.

가장 상세한 정보는 바나흐 알헤브라스라고 불리는 한 부류의 공간에 의해 운반되었다. 이것들은 연속적인 곱셈 연산과 함께 바나흐 공간이다. 중요한 초기 예는 측정 공간 X에서 본질적으로 경계된 측정 가능한 함수의 바나흐 대수였다. 이 함수 집합은 점으로 표시된 덧셈과 스칼라 곱셈 아래의 바나흐 공간이다. 점괘 곱셈의 동작으로, 바나흐 공간의 특수한 타입이 되어, 지금은 교감 폰 노이만 대수라고 부른다. 점 곱하기 X의 제곱합성 함수의 힐버트 공간에서 이 대수학의 표현을 결정한다. 존 폰 노이만의 초기 관찰은 이 서신 또한 역방향으로 작용했다는 것이었다: 약간의 가벼운 기술적 가설을 감안할 때 힐버트 공간에 대한 표현과 함께 상호 작용하는 폰 노이만 대수학이 측정 공간을 결정하는데, 이 두 구성(본 노이만 대수학의 + 측정 공간의 표현과 측정 공간의 표현)은 다음과 같다. 상호 역행의

그 후 폰 노이만은 비협정적 폰 노이만 알헤브라가 상호 교환적 폰 노이만 알헤브라가 그러하듯이 기하학적 의미를 가져야 한다고 제안했다. 프란시스 머레이와 함께 폰 노이만 알헤브라의 분류를 제작했다. 직접 적분 구조는 폰 노이만 대수학을 요인이라 불리는 단순한 알헤브라의 집합으로 분해하는 방법을 보여준다. 폰 노이만과 머레이는 요인을 세 가지 유형으로 분류했다. 1타입은 상쇄 케이스와 거의 동일했다. 타입 II와 타입 III는 새로운 현상을 보였다. 타입 II 폰 노이만 대수학에서는 치수가 단순한 정수가 아니라 어떤 음이 아닌 실수가 될 수 있다는 독특한 특징을 가진 기하학을 결정했다. III형 알헤브라는 I형도 II형도 아닌 알헤브라는 몇십 년의 노력 끝에 이러한 알헤브라는 II형 인자와 밀접한 관계가 있는 것으로 증명되었다.

폰 노이만과 머레이의 요소 분류 작업과 동시에 기능 공간의 기하학적 구조에 대한 약간 다른 접근법. 이 접근법은 C*알제브라의 이론이다. 여기서 동기부여의 예는 C*-${\displaystyle \mathrm{알제브라}}$ $C{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$( X${\displaystyle }$) ${\displaystyle C_{0}(X)}$인데$,$ 여기서 X는 국소적으로 컴팩트한 하우스도르프 위상학적 공간이다. 정의에 따르면, 이것은 포인트와 곱셈의 연산과 함께 무한대(선택한 지점에서 멀리 갈수록 함수가 0에 가까워진다는 것을 느슨하게 의미)에서 사라지는 X의 연속적 복합값 함수의 대수다. Gelfand-Naimark의 정리는 상호 작용 C*-algebras와 기하학적 물체 사이에 다음과 같은 연관성이 있음을 암시했다. 모든 정류형 C*-algebra는 로컬 컴팩트한 Hausdorff 공간 X에 대한$$ ${\displaystyle {C\mathrm{}}_{}}$ $0{\displaystyle {}_{}}$( ${\displaystyle X}$) ${\displaystyle C_{0}(X)$ 형식이다. 따라서 순수하게 상호 작용 C*-알게브라의 관점에서 지역적으로 콤팩트한 하우스도르프 공간을 연구하는 것이 가능하다. 비확정 기하학은 이것을 비확정 C*-알게브라의 연구에 영감을 주는 것으로 받아들인다. If there were such a thing as a "non-commutative space X," then its ${\displaystyle C_{0}(X)}$ would be a non-commutative C*-algebra; if in addition the Gelfand–Naimark theorem applied to these non-existent objects, then spaces (commutative or not) would be the same as C*-algebras; so, for lack of a direct approach to the defin비규격 공간의 반복, 비규격 공간은 비규격 C*-알지브라로 정의된다. 많은 표준 기하학적 도구들은 C*-알게브라의 관점에서 재작성될 수 있으며, 이것은 비고정 C*-알게브라를 연구하는데 기하학적으로 영감을 주는 기술을 제공한다.

이 두 예 모두 이제 비전투 기하학이라고 하는 분야의 예들이다. 폰 노이만 알헤브라와 C*알게브라의 구체적인 예는 각각 비확정적 측정 이론과 비확정적 위상학으로 알려져 있다. 비전투 기하학은 그 자체를 위한 일반성의 추구일 뿐만 아니라 호기심만이 아니다. 비확실성 공간은 일부 구조에서 자연적으로, 심지어 불가피하게 발생하기도 하다. 예를 들어 연과 다트에 의한 비행기의 비주기적 펜로즈 기울기를 생각해 보자. 그런 타일링 속에서 연과 다트의 모든 유한한 조각이 무한히 자주 나타나는 것이 정리다. 따라서 한정된 부분을 보고 두 개의 펜로즈 기울기를 구별할 방법이 없다. 이것은 전통적인 의미의 토폴로지를 모든 기울기 집합을 할당하는 것을 불가능하게 만든다. 그럼에도 불구하고, 펜로즈 기울기는 비확정 C*-알제브라를 결정하며, 결과적으로 비확정 기하학의 기법에 의해 연구될 수 있다. 또 다른 예와 미분 기하학 내에서 큰 관심사 중 하나는 다지관의 분리로부터 온다. 이것들은 다지관을 잎이라고 불리는 더 작은 차원 서브매니폴드로 분할하는 방법인데, 각각은 근처의 다른 것과 국소적으로 평행하다. 모든 잎들의 집합은 위상학적 공간으로 만들어질 수 있다. 그러나 비합리적인 회전의 예는 이 위상학적 공간이 고전적 측량 이론의 기법으로는 불충분할 수 있다는 것을 보여준다. 그러나 엽의 잎 공간과 연관된 비확정적 폰 노이만 대수학이 있으며, 다시 한번 이것은 달리 알아들을 수 없는 공간에 좋은 기하학적 구조를 준다.

구성표

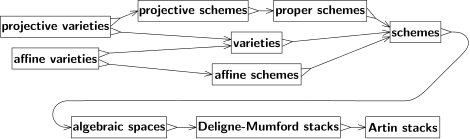
대수 기하학은 다항식의 기하학적 특성을 연구한다. 다항식은 덧셈과 곱셈의 기본 산술 연산에서 정의한 함수 유형이다. 이 때문에 대수학과는 밀접한 관계가 있다. 대수 기하학은 순수한 대수학 문제에 기하학적 기법을 적용하는 방법을 제공하며, 그 반대의 경우도 마찬가지다.

1940년대 이전에는 복잡한 숫자에 대해 대수 기하학이 독점적으로 작용했고, 가장 근본적인 다양성은 투영 공간이었다. 투사 공간의 기하학은 원근 이론과 밀접한 관련이 있으며, 그 대수학은 동종 다항식으로 기술된다. 다른 모든 품종은 투영 공간의 하위 집합으로 정의되었다. 투영 품종은 동종 다항식 집합에 의해 정의된 하위 집합이었다. 투영 버라이어티의 각 지점에서 집합의 모든 다항식은 0이 되어야 했다. 선형 다항식의 영점 집합의 보어는 아핀 공간이며, 아핀 다양성은 아핀 공간과 투영적인 다양성의 교차점이었다.

안드레 웨일은 기하학적 추론이 때때로 문제의 공간이 이산적이거나 심지어 유한적일 수 있는 수 이론적 상황에 적용될 수 있다고 보았다. 이러한 사상을 추구하면서 Weil은 대수기하학의 기초를 다시 썼는데, 둘 다 복잡한 숫자에 대한 의존에서 대수기하학을 해방시키고 투영적인 공간에 내장되지 않은 추상기하학 품종을 도입했다. 이것들은 이제 단순히 품종이라고 불린다.

현대 대수 기하학의 기초가 되는 공간의 유형은 웨일의 추상 대수학 변종보다 훨씬 일반적이다. 알렉산더 그로텐디크에 의해 소개되었고 계략이라고 불린다. 계략 이론의 동기 중 하나는 다항식들이 함수들 사이에서 유별나게 구조화되어 있고, 대수적 다양성은 결과적으로 경직되어 있다는 것이다. 이것은 퇴폐적인 상황을 연구하려고 할 때 문제를 일으킨다. 예를 들어 원 위의 거의 모든 점 쌍은 제분선이라는 고유한 선을 결정하며, 두 점이 원을 중심으로 이동함에 따라 제분선은 연속적으로 변화한다. 그러나 두 점이 충돌하면 이차선은 접선선으로 변한다. 접선 선은 독특하지만, 이 구성의 기하학, 즉 원의 한 점은 독특한 선을 결정하기에 충분히 표현되지 않는다. 이런 상황을 연구하려면 퇴보한 상황에 추가 자료를 할당할 수 있는 이론이 필요하다.

계획의 구성 요소 중 하나는 위상학적 공간이다. 위상학적 공간은 연속적인 기능을 가지고 있지만, 연속적인 기능은 관심의 근본적인 대수 구조를 반영하기에는 너무 일반적이다. 그러므로 어떤 계획의 또 다른 성분은 위상학적 공간에 있는 피복으로, "구조 피복"이라고 불린다. 위상학적 공간의 각 열린 부분 집합에서, 피복은 "정규적 함수"라고 불리는 함수의 집합을 지정한다. 위상학적 공간과 구조 피복이 함께 있어야 함수가 대수적 연산으로부터 나온다는 것을 의미하는 조건을 만족시킬 수 있다.

다지관과 마찬가지로 체계는 친숙한 공간에서 국소적으로 모델링된 공간으로 정의된다. 다지관의 경우 익숙한 공간이 유클리드 공간이다. 어떤 계획을 위해, 지역 모델들은 애프라인 체계라고 불린다. 아핀 체계는 대수 기하학과 정류 대수학 사이에 직접적인 연관성을 제공한다. 역학대수학에서 연구할 수 있는 기초적인 대상은 역학 고리들이다. $R{\displaystyle }$ ${\displaystyle R}$이(가) 정류 링이면$$ R${\displaystyle$ $\operatorname {Spec}$ R$}$의 대수 $구조$를 지오메트리로 변환하는$$$$ 해당 부속 체계 ${\displaystyle \mathrm{Spec}}$이 있다. 반대로, 모든 부속 체계는 서로 다른 고리, 즉 구조물의 전지구적 부분의 링을 결정한다. 이 두 연산은 상호 역행적이므로, 부속 체계는 역행 대수학에서 문제를 연구할 수 있는 새로운 언어를 제공한다. 정의에 따르면, 어떤 계획의 모든 포인트는 열린 이웃을 가지고 있는데, 그것은 친근한 계획이다.

그 계획에는 부합되지 않는 것이 많다. 특히 투영 공간은 압축성과 유사한 적정성이라는 조건을 만족시킨다. 부속 계획은 적절할 수 없으며(계획이 단일 점만을 갖는 경우와 같은 사소한 상황의 경우는 제외), 따라서 어떤 투영 공간도 부속 체계(제로차원 투영 공간 제외)가 아니다. 투사적 계획은 투사적 공간의 폐쇄적 자원으로서 발생하는 것을 의미하며, 가장 중요한 계획의 단일 가족이다.^[12]

여러 가지 계획의 일반화가 도입되었다. 마이클 아르틴은 대수적 공간을 에탄올 형태론을 정의하는 동등성 관계에 의한 계획의 몫으로 정의했다. 대수적 공간은 계획들의 많은 유용한 특성들을 보유하면서 동시에 더 유연하다. 예를 들어, 킬-모리 정리는 많은 모듈리 공간이 대수적 공간이라는 것을 보여주기 위해 사용될 수 있다.

대수적 공간보다 더 일반적인 것은 Deligne-Mumford 스택이다. DM 스택은 체계와 유사하지만, 다항식 측면에서만 설명할 수 없는 특이점을 허용한다. 그들은 오비폴드가 다지관을 위해 하는 계획에도 같은 역할을 한다. 예를 들어 원점 주위의 유한한 회전 그룹에 의한 아핀 평면의 몫은 계략이나 대수적 공간이 아닌 델리뉴-엠포드 스택을 산출한다. 원점에서 벗어나, 그룹 작용에 의한 몫은 원의 동일한 간격의 점들의 유한 집합을 식별한다. 그러나 원점에서 원은 하나의 점, 즉 원점 그 자체로만 구성되며 집단행동이 이 점을 고친다. 그러나, 지수 DM 스택에서 이 지점은 지수라는 추가 데이터와 함께 나온다. 이런 종류의 정제된 구조는 모듈리 공간 이론에 유용하며, 사실 원래 대수곡선의 모듈리를 기술하기 위해 도입되었다.

추가적인 일반화는 Artin 스택이라고도 불리는 대수적 스택이다. DM 스택은 유한 그룹 작업에 의한 인수로 제한된다. 이것이 모듈리 이론의 많은 문제들에 대해 충분하지만, 그것은 다른 사람들에게는 너무 제한적이며, Artin 스택은 더 많은 일반적인 인용구를 허용한다.

토포이

그는 Weil 추측에 관한 Grotendieck의 연구에서 현재 Grotendieck 위상이라고 불리는 새로운 형태의 위상을 소개했다. 위상학적 공간(일반적인 의미에서의)은 "근접성"의 개념을 공리화하여, 만약 그것들이 같은 오픈 세트의 많은 부분에 놓여있다면 두 점을 가까이 두게 한다. 이와는 대조적으로, 그로텐디크 위상은 "커버링"이라는 개념을 공리화한다. 공간의 커버는 주변 공간의 모든 정보를 공동으로 포함하는 서브 스페이스 모음입니다. 피복의 관점에서 피복(covering)을 정의하기 때문에, 그로텐디크 위상은 피복 이론의 공리화라고도 볼 수 있다.

그로텐디크의 토폴로지 연구는 그를 토포이 이론으로 이끌었다. 그는 회고록 레콜테스 외 세마유에서 그들을 "가장 방대한 구상"^[13]이라고 불렀다. 피복(위상학적 공간에 있거나 그로텐디크 위상에 관한 것)은 지역 데이터를 표현하기 위해 사용된다. 모든 피복의 범주는 지역 데이터를 표현하는 가능한 모든 방법을 포함한다. 위상학적 공간은 그 자체가 일종의 국부적 자료인 점으로부터 구성되기 때문에, 따라서 피복의 범주는 원래의 공간의 대체물로 사용될 수 있다. 그로텐디크는 결과적으로 토포들을 셰이브의 범주로 정의하고 토포이를 그들 자신의 권리에 대한 관심의 대상으로 연구했다. 이것들은 현재 그로텐디크 토포이라고 불린다.

모든 위상학적 공간은 위상을 결정하며, 그 반대의 경우도 위상을 결정한다. 관련 토포들을 복용하는 것이 정보를 잃는 위상학적 공간들이 있지만, 이것들은 일반적으로 병적인 것으로 간주된다. (위상학적 공간은 냉정한 공간이라는 것이 필요하고도 충분한 조건이다.) 반대로 연관된 위상학적 공간이 원래의 토포들을 포착하지 못하는 토포이가 있다. 그러나 병적인 것과는 거리가 먼 이 토포이들은 수학적 관심사가 될 수 있다. 예를 들어, 그로텐디크의 에탈 코호몰로지 이론(결국 웨일 추측의 증거로 이어졌다)은 어떤 계획의 에텔 토포에서 코호몰로지라고 표현될 수 있으며, 이 토포들은 위상학적 공간에서 나온 것이 아니다.

위상학적 공간은 사실 locales라고 불리는 매우 특별한 topoi로 이어진다. 위상학적 공간의 열린 하위 집합 집합이 격자를 결정한다. 위상학적 공간에 대한 공리는 이들 격자가 완전한 헤잉 알헤브라스(Heyting Algebras)가 되게 한다. 국지론은 이것을 출발점으로 삼는다. 로케일은 완전한 헤이팅 대수학으로 정의되며, 위상학적 공간의 기본적인 성질은 이러한 용어로 다시 표현되고 책망된다. 로케일의 개념은 위상학적 공간보다 더 일반적인 것으로 판명되는데, 모든 냉정한 위상학적 공간은 독특한 로케일을 결정하지만, 많은 흥미로운 지역들은 위상학적 공간으로부터 오는 것이 아니다. 로케인은 포인트가 필요 없기 때문에 로케스에 대한 연구는 다소 농담으로 무의미한 토폴로지라고 불린다.

Topoi는 또한 수학 논리와 깊은 연관성을 보여준다. 모든 그로텐디크 토포스는 하위 개체 분류기라고 불리는 특별한 피자를 가지고 있다. 이 하위 객체 분류기는 가능한 모든 진실 값의 집합과 같은 기능을 한다. 세트의 토포에서 하위 개체 분류자는 "거짓" 및 "참"에 해당하는$\{$${\displaystyle 0,}$ ${\displaystyle 1}$ ${\displaystyle \}}$ ${\displaystyle \{0,1\}}$ 집합이다. 그러나 다른 topoi에서는 하위 객체 분류기가 훨씬 더 복잡할 수 있다. 로베레와 티어니는 부객체 분류기를 공리화하면 현재 초등 토포라고 알려진 보다 일반적인 종류의 토포들이 산출되고, 초등 토포이가 직관적 논리의 모델이라는 것을 인식했다. 논리학에서 기하학으로 도구를 적용하는 강력한 방법을 제공하는 것 외에도, 이것은 논리학에서 기하학적 방법의 사용을 가능하게 했다.

공간 및 구조

케빈 칼슨에 따르면

이러한 단어 ["공간"과 "구조"는 모두 하나의 수학적 정의를 가지고 있지 않다. 영어 단어들은 본질적으로 모두 같은 상황에서 사용될 수 있지만, 당신은 종종 "공간"을 더 기하학적으로, 그리고 "구조"를 더 대수학적으로 생각한다. [...] 그러므로 당신은 우리가 대수학을 하는 장소로서 "구조"를, 그리고 "공간"을 우리가 기하학을 하는 장소로서 생각할 수 있다. 그 후 위상학적 공간의 기본 집단이나 반지의 스펙트럼을 볼 때, 많은 훌륭한 수학들이 구조에서 우주로, 그리고 그 반대로 왔다. 그러나 결국 그 구별은 어렵지도 않고 빠르지도 않으며, 단지 멀리까지 갈 뿐이다: 많은 것들이 분명히 구조와 공간 둘 다일 뿐이고, 어떤 것들은 분명히 둘 다 아니며, 어떤 사람들은 내가 여기서 말한 모든 것에 반대할 수도 있다.^[1]

그럼에도 불구하고, Bourbaki에 의해 "구조"에 대한 일반적인 정의가 제안되었다;^[2] 그것은 위에서 언급된 모든 종류의 공간, 지금까지 사용된 모든 유형의 수학적 구조, 그리고 그 이상을 포함한다. 그것은 이형성에 대한 일반적인 정의를 제공하며, 이형 구조들 간의 특성 이전을 정당화한다. 그러나 수학적 실무에서는 결코 적극적으로 사용되지 않았다(부르바키 자신이 쓴 수학적 논문에서도 그렇지 않다). 다음은 레오 코리(Leo Corry)가 쓴 책의 로버트 리드(Robert Reed^[14]) 리뷰의 마지막 구절이다.

코리는 구조의 어떤 형식적인 정의가 실제 수학 실습에서 개념의 사용에 정의로 작용할 수 있다고 느끼지 않는 것 같다[...] 코리의 견해는 '구조'가 본질적으로 수학을 하는 방법을 의미한다는 믿음으로 요약될 수 있으며, 따라서 c와 같이 정확하게 정의될 수 있는 개념과는 아마도 거리가 먼 개념일 것이다.수학 자체의 초경량적 유물

수학적 구조에 대한 자세한 내용은 위키백과:수학적 구조, 수학적 구조의 동등한 정의 및 구조 수송을 참조하십시오.

기하학적 "공간"과 대수학적 "구조"의 구별은 때로는 분명하고 때로는 이해하기 어렵다. 분명히 그룹은 대수학인 반면 유클리드 공간은 기하학적이다. 링 위의 모듈은 그룹만큼 대수적이다. 특히 링이 필드인 것처럼 보일 때 모듈이 선형공간으로 나타난다. 대수학적인가 기하학적인가? 특히, 그것이 유한한 차원이고, 실수에 넘치고, 내적인 산물이 부여되면, 그것은 유클리드 공간이 되고, 지금은 기하학적인 공간이 된다. 실수의 (알지브라틱?) 필드는 실선과 같다. 그것의 대수학적 폐쇄, 복잡한 숫자의 (알지브라틱?) 장은 (기하학?) 복잡한 평면과 같다. 우선 "우리가 분석하는 장소"(대수나 기하학보다는)이다.

위의 "비확정 기하학", "구성표" 및 "토포이" 하위 섹션을 제외하고 위의 "공간 유형"에서 처리되는 모든 공간은 구조물의 집합(Bourbaki에 따르면 구조의 "주요 기초 집합")이며, 기본 세트의 요소는 대개 이 공간의 "점"이라고 불린다. 대조적으로 대수 구조의 (기본 집합) 요소는 대개 "점"이라고 불리지 않는다.

그러나 때때로 둘 이상의 기본 세트를 사용한다. 예를 들어, 2차원 투영 기하학은 점 집합과 선 집합이라는 두 개의 기본 집합을 통해 공식화될 수 있다. 더욱이 투사 평면의 두드러진 특징은 점과 선에 의해 행해지는 역할의 대칭성이다. 덜 기하학적인 예: 정점 집합(노드 또는 점이라고도 함)과 가장자리 집합(호 또는 선이라고도 함)을 통해 그래프를 공식화할 수 있다. 일반적으로 부르바키가 규정하는 기본 베이스 세트와 보조 베이스 세트가 상당히 많다.

위의 "비확정 기하학", "구성표" 및 "토포이" 하위 절에서 처리되는 기하학적 맛의 많은 수학 구조는 기준점 집합을 규정하지 않는다. 예를 들어, "무점 위상"(즉, 점 없는 위상 또는 로케일 이론)은 위상학적 공간에서 요소들이 열린 세트를 모방하는 단일 베이스 집합으로 시작한다(점 집합은 아님). 단순한 점학 및 점 없는 기하학도 참조한다.

이름별 수학적 공간

참고 항목

• 수학적 구조
• 구조물의 운송
• 설정(수학)

메모들

각주

참조

이 기사는 2017년 외부 학술 동료 검토를 위해 위키저널 사이언스지에 제출되었다(검토자 보고서). 업데이트된 콘텐츠는 CC-BY-SA-3.0 라이센스(2018)에 따라 위키백과 페이지로 다시 통합되었다. 검토된 기록의 버전은 다음과 같다.

• Bourbaki, Nicolas, Elements of mathematics, Hermann (original), Addison-Wesley (translation).
• Bourbaki, Nicolas (1968), Elements of mathematics: Theory of sets, Hermann (original), Addison-Wesley (translation).
• Eisenbud, David; Harris, Joe (2000), The Geometry of Schemes, Springer-Verlag, doi:10.1007/b97680, ISBN 978-0-387-98638-8.
• Gowers, Timothy; Barrow-Green, June; Leader, Imre, eds. (2008), The Princeton Companion to Mathematics, Princeton University Press, ISBN 978-0-691-11880-2.
• Itô, Kiyosi, ed. (1993), Encyclopedic dictionary of mathematics (second ed.), Mathematical society of Japan (original), MIT press (translation).

외부 링크

• Wikimedia Commons의 공간 관련 미디어(수학)
• 마틸드 마르콜리 (Matilde Marcolli, 2009) 수학의 공간 개념, 칼텍으로부터.