추정통계

Estimation statistics
추정 이론과 혼동해서는안 된다.
다른 용도는 추정(동음이의)을 참조하십시오.

추정 통계량 또는 단순 추정은 효과 크기, 신뢰 구간, 정밀 계획 및 메타 분석의 조합을 사용하여 실험을 계획하고 데이터를 분석하며 결과를 해석하는 데이터 분석 프레임워크다.[1] 그것은 덜 유익하다고 여겨지는 귀무 가설 유의성 시험(NHST)과는 구별된다.[2][3] 추정 통계는 심리학, 의학 연구, 생명 과학, 그리고 다른 실험 과학 분야의 새로운[3] 통계로도 알려져 있는데, NHT는 수십 년 동안 반대되는 권고에도 불구하고 여전히 널리 퍼져 있다.[4][5]

추정 방법의 주요 목적은 신뢰 구간과 함께 효과 크기(점 추정치)를 보고하는 것이며, 그 중 후자는 추정의 정밀도와 관련이 있다.[6] 신뢰 구간은 기초 모집단 효과의 가능한 값의 범위를 요약한다. 추정의 지지자들은 P값을 보고하는 것을 신뢰 구간으로 보고 효과 크기를 보고하는 중요한 사업에서 벗어나는 데 도움이 되지 않는 것으로 보고,[7] 추정이 데이터 분석을 위한 유의성 검사를 대체해야 한다고 믿는다.[8] 그럼에도 불구하고 p-값과 신뢰 구간은 동일한 동전의 양면이며 동일한 유형의 정보를 제공하기 때문에 이는 오해의 소지가 있다.[9]

역사

1929년부터 물리학자인 레이먼드 테이어 버지는 가중 평균 방법을 사용하여 물리적 상수의 추정치를 계산하는 리뷰 논문을[10] 발표했는데, 이는 현대 메타분석의 전조로 볼 수 있는 절차다.[11]

1960년대에 추정 통계는 제이콥 코헨에 의한 표준화된 효과 크기의 개발로 비물리적 과학에 의해 채택되었다.

1970년대에는 진V에 의해 근대 연구 합성이 개척되었다. 심리치료를 위한 첫 번째 체계적 검토와 메타분석이 있는 유리.[12] 이러한 선구적인 작업은 이후 의료 치료를 위한 메타 분석의 채택에 더 일반적으로 영향을 미쳤다.

1980년대와 1990년대에는 래리 헤지스, 마이클 보렌스타인, 더그 알트먼, 마틴 가드너 등 생물통계학자들이 현대(의료) 메타분석의 발달로 추정 방법을 확장하고 다듬었다.

1980년대부터 메타분석과 연계해 사용된 체계적 검토는 의학 연구에 널리 사용되는 기법이 되었다. PubMed에는 "메타 분석"에 대한 인용구가 20만 건이 넘는다.

1990년대에, 편집자 Kenneth Rothman은 역학 저널에 p-값의 사용을 금지했다; 작가들 사이에서 준수성이 높았지만, 이것은 그들의 분석적 사고를 실질적으로 바꾸지는 않았다.[13]

2010년대에 제프 커밍은 주로 심리학자들에게 효과적 사고를 가르치기 위해 고안된 엑셀의 소프트웨어와 함께 추정 통계학을 전문으로 하는 교과서를 출판했다.[14] 또한 2010년대에는 신경과학에서 추정 방법이 점점 더 많이 채택되었다.[15][16]

2013년 미국심리학회 출판매뉴얼에서는 가설검사에 대한 추정을 권고했다.[17] 또한 2013년, 생물 의학 저널에 제출된 원고에 대한 통일 요구사항 문서도 유사한 권고안을 제시하였다. "효과 크기에 대한 중요한 정보를 전달하지 못하는 P 값과 같은 통계적 가설 시험에만 의존하지 않도록 한다."[18]

2019년 신경과학저널 eNeuro는 데이터 제시를 위한 선호 방법으로 추정 그래픽 사용을 권장하는 정책을 제정했다.[19]

임상 연구를 위한 메타 분석의 채택과 몇몇 주요 출판 기관의 권고에도 불구하고, 추정 프레임워크는 일차 생물의학 연구에 일상적으로 사용되지 않는다.[20]

방법론

많은 유의성 시험에는 추정 상대가 있다.[21] 거의 모든 경우에 시험 결과(또는 그 p-값)는 단순히 효과 크기와 정밀도 추정치로 대체될 수 있다. 예를 들어, 분석가는 학생의 t-검정을 사용하는 대신 평균 차이와 95% 신뢰 구간을 계산하여 두 개의 독립적인 그룹을 비교할 수 있다. 해당 방법은 쌍체 t-검정 및 다중 비교에 사용할 수 있다. 마찬가지로 회귀 분석의 경우 분석가는 모형의 p-값 대신 결정 계수(R2)와 모형 방정식을 보고할 수 있다.

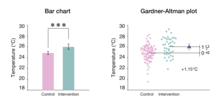
그러나 추정 통계에 찬성하는 사람들은 단지 몇 개의 숫자만을 보고하지 말라고 경고한다. 오히려 데이터 시각화를 이용해 데이터를 분석하고 제시하는 것이 좋다.[2][5][6] 적절한 시각화의 예로는 회귀 분석을 위한 산점도 및 두 개의 독립 그룹에 대한 가드너-알트만 그림을 들 수 있다.[22] 과거 데이터 그룹 그림(막대 차트, 상자 그림 및 바이올린 그림)은 비교를 표시하지 않지만 추정 그림은 두 번째 축을 추가하여 효과 크기를 명시적으로 시각화한다.[23]

가드너-알트만 줄거리. 왼쪽: 아스테리스크를 사용하여 '통계적으로 유의함'을 나타내는 전통적인 막대 차트. 오른쪽: 모든 데이터 점과 평균 차이 및 신뢰 구간을 표시하는 Gardner-Altman 그림.

가드너-알트만 플롯

가드너-알트만 평균 차이 그림은 1986년 마틴 가드너와 더그 알트먼에 의해 처음 설명되었다.[22][5] 이것은 두 개의 독립적인 그룹의 데이터를 표시하도록 설계된 통계 그래프다. 쌍체 데이터에 적합한 버전도 있다. 이 차트를 만드는 주요 지침은 (1) 두 그룹에 대해 관찰된 모든 값을 나란히 표시, (2) 두 번째 축을 오른쪽에 놓고, 평균 차이 척도를 표시하도록 이동, (3) 오차 막대가 있는 마커로 신뢰 구간으로 평균 차이를 표시한다.[3] 가드너-Altman 플롯은 DABEST-Python 또는 DABestr로 생성될 수 있으며, 분석가는 추정 통계 앱과 같은 GUI 소프트웨어를 사용할 수도 있다.

커밍 줄거리. ProvalingStats 웹 응용 프로그램에서 렌더링한 커밍 플롯. 상단 패널에는 관측된 모든 값이 표시된다. 효과 크기, 표본 분포 및 95% 신뢰 구간은 원시 데이터 아래의 별도 축에 표시된다. 각 그룹에 대해, 요약 측정(평균 ± 표준 편차)을 가선(gap)으로 그린다.

커밍 플롯

여러 그룹에 대해 제프 커밍은 관측값 패널 아래에 있는 두 개 이상의 평균 차이와 신뢰 구간을 표시하기 위해 보조 패널을 사용하였다.[3] 이 배열은 여러 데이터 그룹에 대한 평균 차이('deltas')를 쉽게 비교할 수 있게 한다. 커밍 플롯은 ESCI 패키지, DABEST 또는 추정 통계 앱을 통해 생성할 수 있다.

기타 방법론

평균 차이 외에도, 상대적 편익을 가진 다른 효과 크기 유형들이 많이 있다. 주요 유형에는 코헨의 표준화된 측정 기준 d등급에 있는 효과 크기, 회귀 분석을 위한 결정 계수(R2)가 포함된다. 비정규 분포의 경우 클리프의 델타 및 콜모고로프-스미르노프 통계량을 포함하여 여러 가지 더 강력한 효과 크기가 있다.

가설 검정의 결함

주요 기사: 통계적 가설 검정 § 비평
참고 항목: p-값 § 비평 및 p-값 오용

가설 검정에서, 통계적 계산의 주요 목적은 귀무 가설이 참이라고 가정했을 때 p-값, 얻어진 결과를 볼 확률 또는 더 극단적인 결과를 얻는 것이다. p-값이 낮으면(일반적으로 < 0.05>), 통계적 실무자는 귀무 가설을 기각하도록 권장한다. 추정의 지지자들은 다음과 같은 이유로 가설 검사의[3][6] 타당성을 거부한다.

  • P-값은 쉽고 일반적으로 잘못 해석된다. 예를 들어 p-값은 종종 '귀무 가설이 참일 확률'로 잘못 생각되는 경우가 많다.
  • 귀무 가설은 관측치의 모든 집합에 대해 항상 틀린다: 비록 그것이 미미하더라도 항상 약간의 효과가 있다.[24]
  • 가설검사는 규모에 대한 중요한 정보를 삭제하면서 임의로 이분법적인 예-아니오 답변을 생성한다.[25]
  • 특정 p-값은 효과 크기, 표본 크기(모든 물체가 더 큰 표본 크기가 더 작은 p-값을 생성함)와 표본 오차의 상호작용을 통해 발생한다.[26]
  • 저전력에서 시뮬레이션은 샘플링 오차가 p-값을 극도로 변동하게 만든다는 것을 보여준다.[27]

추정 통계량의 이점

신뢰 구간의 장점

신뢰 구간은 예측 가능한 방식으로 작용한다. 정의에 따르면 95% 신뢰 구간은 기초 모집단 평균(μ)을 포함할 확률이 95%이다. 이 기능은 표본 크기가 증가해도 일정하게 유지되며, 변경되는 것은 간격이 작아진다는 것이다. 또한 95% 신뢰 구간은 예측 구간 83%이다. 즉, 하나의 (사전 실험) 신뢰 구간은 미래 실험의 평균을 포함할 확률이 83%이다.[3] 따라서 단일 실험의 95% 신뢰 구간을 알면 분석가는 모집단 평균에 대한 합리적인 범위를 얻을 수 있다. 그럼에도 불구하고 신뢰 분포와 후방 분포는 단일 점 추정치나 간격보다 훨씬 더 많은 정보를 제공하며,[28] 관심의 "null" 값을 포함하거나 포함하지 않는 간격에 따라 이분법적 사고(즉, 피셔의[29] 그것과 반대로 Neyman의 귀납적 행동)를 악화시킬 수 있다.

증거 기반 통계

통계 인식에 대한 심리학적 연구는 보고 간격 추정치가 p-값을 보고하는 것보다 데이터에 대한 더 정확한 인식을 남긴다는 것을 보여준다.[30]

정밀계획

추정의 정밀도는 공식적으로 1/분산이라고 정의되며 검정력과 마찬가지로 표본 크기가 증가할수록 증가(개선)한다. 전력과 마찬가지로 높은 수준의 정밀도는 비용이 많이 든다. 연구 보조금 신청은 이상적으로 정밀도/비용 분석을 포함할 것이다. 추정의 지지자들은 통계적 힘 자체는 유의성 시험과 개념적으로 연관되어 있기 때문에 정밀 계획이 전력을 대체해야 한다고 생각한다.[3] 정밀기획은 ESCI 웹앱으로 할 수 있다.

참고 항목

참조

  1. ^ Ellis, Paul. "Effect size FAQ".
  2. ^ a b Cohen, Jacob. "The earth is round (p<.05)" (PDF).
  3. ^ a b c d e f g Cumming, Geoff (2011). Understanding The New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis. New York: Routledge. ISBN 978-0415879675.[페이지 필요]
  4. ^ Altman, Douglas (1991). Practical Statistics For Medical Research. London: Chapman and Hall.
  5. ^ a b c Douglas Altman, ed. (2000). Statistics with Confidence. London: Wiley-Blackwell.[페이지 필요]
  6. ^ a b c Cohen, Jacob (1990). "Things I have learned (so far)". American Psychologist. 45 (12): 1304–1312. doi:10.1037/0003-066x.45.12.1304.
  7. ^ Ellis, Paul (2010-05-31). "Why can't I just judge my result by looking at the p value?". Retrieved 5 June 2013.
  8. ^ Claridge-Chang, Adam; Assam, Pryseley N (February 2016). "Estimation statistics should replace significance testing". Nature Methods. 13 (2): 108–109. doi:10.1038/nmeth.3729. PMID 26820542. S2CID 205424566.
  9. ^ Poole, Charles (May 2001). "Low P-Values or Narrow Confidence Intervals: Which Are More Durable?". Epidemiology. 12 (3): 291–294. doi:10.1097/00001648-200105000-00005. PMID 11337599. S2CID 29892284.
  10. ^ Birge, Raymond T. (1 July 1929). "Probable Values of the General Physical Constants". Reviews of Modern Physics. 1 (1): 1–73. Bibcode:1929RvMP....1....1B. doi:10.1103/RevModPhys.1.1.
  11. ^ Hedges, Larry (1987). "How hard is hard science, how soft is soft science". American Psychologist. 42 (5): 443. CiteSeerX 10.1.1.408.2317. doi:10.1037/0003-066x.42.5.443.
  12. ^ Hunt, Morton (1997). How science takes stock: the story of meta-analysis. New York: The Russell Sage Foundation. ISBN 978-0-87154-398-1.
  13. ^ Fidler, Fiona; Thomason, Neil; Cumming, Geoff; Finch, Sue; Leeman, Joanna (February 2004). "Editors Can Lead Researchers to Confidence Intervals, but Can't Make Them Think: Statistical Reform Lessons From Medicine". Psychological Science. 15 (2): 119–126. doi:10.1111/j.0963-7214.2004.01502008.x. PMID 14738519. S2CID 21199094.
  14. ^ Cumming, Geoff. "ESCI (Exploratory Software for Confidence Intervals)".
  15. ^ Yildizoglu, Tugce; Weislogel, Jan-Marek; Mohammad, Farhan; Chan, Edwin S.-Y.; Assam, Pryseley N.; Claridge-Chang, Adam (8 December 2015). "Estimating Information Processing in a Memory System: The Utility of Meta-analytic Methods for Genetics". PLOS Genetics. 11 (12): e1005718. doi:10.1371/journal.pgen.1005718. PMC 4672901. PMID 26647168.
  16. ^ Hentschke, Harald; Maik C. Stüttgen (December 2011). "Computation of measures of effect size for neuroscience data sets". European Journal of Neuroscience. 34 (12): 1887–1894. doi:10.1111/j.1460-9568.2011.07902.x. PMID 22082031. S2CID 12505606.
  17. ^ "Publication Manual of the American Psychological Association, Sixth Edition". Retrieved 17 May 2013.
  18. ^ "Uniform Requirements for Manuscripts Submitted to Biomedical Journals". Archived from the original on 15 May 2013. Retrieved 17 May 2013.
  19. ^ Bernard, Christophe (July 2019). "Changing the Way We Report, Interpret, and Discuss Our Results to Rebuild Trust in Our Research". eNeuro. 6 (4). doi:10.1523/ENEURO.0259-19.2019. PMC 6709206. PMID 31453315.
  20. ^ Halsey, Lewis G. (31 May 2019). "The reign of the p -value is over: what alternative analyses could we employ to fill the power vacuum?". Biology Letters. 15 (5): 20190174. doi:10.1098/rsbl.2019.0174. PMC 6548726. PMID 31113309.
  21. ^ Cumming, Geoff; Calin-Jageman, Robert (2016). Introduction to the New Statistics: Estimation, Open Science, and Beyond. Routledge. ISBN 978-1138825529.[페이지 필요]
  22. ^ a b Gardner, M J; Altman, D G (15 March 1986). "Confidence intervals rather than P values: estimation rather than hypothesis testing". BMJ. 292 (6522): 746–750. doi:10.1136/bmj.292.6522.746. PMC 1339793. PMID 3082422.
  23. ^ Ho, Joses; Tumkaya, Tayfun; Aryal, Sameer; Choi, Hyungwon; Claridge-Chang, Adam (26 July 2018). "Moving beyond P values: Everyday data analysis with estimation plots". doi:10.1101/377978. Cite 저널은 필요로 한다. journal= (도움말)
  24. ^ Cohen, Jacob (1994). "The earth is round (p < .05)". American Psychologist. 49 (12): 997–1003. doi:10.1037/0003-066X.49.12.997.
  25. ^ Ellis, Paul (2010). The Essential Guide to Effect Sizes: Statistical Power, Meta-Analysis, and the Interpretation of Research Results. Cambridge: Cambridge University Press.[페이지 필요]
  26. ^ Denton E. Morrison, Ramon E. Henkel, ed. (2006). The Significance Test Controversy: A Reader. Aldine Transaction. ISBN 978-0202308791.[페이지 필요]
  27. ^ Cumming, Geoff. "Dance of the p values".
  28. ^ Xie, Min-ge; Singh, Kesar (2013). "Confidence Distribution, the Frequentist Distribution Estimator of a Parameter: A Review". International Statistical Review. 81 (1): 3–39. doi:10.1111/insr.12000. JSTOR 43298799.
  29. ^ Halpin, Peter F.; Stam, Henderikus J. (2006). "Inductive Inference or Inductive Behavior: Fisher and Neyman: Pearson Approaches to Statistical Testing in Psychological Research (1940-1960)". The American Journal of Psychology. 119 (4): 625–653. doi:10.2307/20445367. JSTOR 20445367. PMID 17286092.
  30. ^ Beyth-Marom, Ruth; Fidler, Fiona Margaret; Cumming, Geoffrey David (2008). "Statistical cognition: Towards evidence-based practice in statistics and statistics education". Statistics Education Research Journal. 7: 20–39. CiteSeerX 10.1.1.154.7648.