블록 쌓기 문제
Block-stacking problem통계학에서, 블록 쌓기 문제(때로는 리어의 기울어진 탑(Johnson 1955)로 알려져 있기도 하고, 책 쌓기 문제 또는 그 밖의 여러 유사한 용어)는 테이블 가장자리에 블록 쌓기에 관한 퍼즐이다.
성명서
블록 쌓기 문제는 다음과 같은 퍼즐이다.
오버행(overhang)을 최대화할 수 있도록 가장자리의 안정적 스택에 N {\과(와 동일한 강체 직사각형 블록을 배치하십시오.
패터슨 외 (2007)은 19세기 중반부터 역학 문헌으로 거슬러 올라가는 이 문제에 대한 긴 참고 문헌 목록을 제공한다.
변형
싱글 와이드
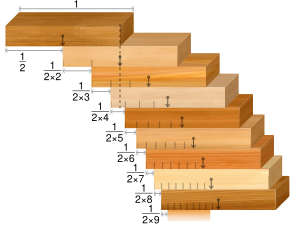
단일 범위 문제는 주어진 수준에서 한 블록만 갖는 것을 포함한다.완벽하게 직사각형 블록의 이상적인 경우, 단일 폭 문제에 대한 해결책은 최대 돌출부가 블록 폭의 i= 1 {1에 의해 주어진다는 것이다.이 합은 해당 고조파 계열의 부분 합계의 절반이다.고조파 계열이 분산되기 때문에 오버행은 N {\displaystyle 이(가 증가함에 따라 무한대로 되는 경향이 있으며, 이는 충분한 블록으로 임의적으로 큰 오버행(overhang)을 달성할 수 있다는 것을 의미한다.
| N | 최대 돌출부 | |||
|---|---|---|---|---|
| 분수로 표현된 | 십진법의 | 상대적 크기 | ||
| 1 | 1 | /2 | 0.5 | |
| 2 | 3 | /4 | 0.75 | |
| 3 | 11 | /12 | ~0.91667 | |
| 4 | 25 | /24 | ~1.04167 | |
| 5 | 137 | /120 | ~1.14167 | |
| 6 | 49 | /40 | 1.225 | |
| 7 | 363 | /280 | ~1.29643 | |
| 8 | 761 | /560 | ~1.35893 | |
| 9 | 7 129 | /5 040 | ~1.41448 | |
| 10 | 7 381 | /5 040 | ~1.46448 | |
| N | 최대 돌출부 | |||
|---|---|---|---|---|
| 분수로 표현된 | 십진법의 | 상대적 크기 | ||
| 11 | 83 711 | /55 440 | ~1.50994 | |
| 12 | 86 021 | /55 440 | ~1.55161 | |
| 13 | 1 145 993 | /720 720 | ~1.59007 | |
| 14 | 1 171 733 | /720 720 | ~1.62578 | |
| 15 | 1 195 757 | /720 720 | ~1.65911 | |
| 16 | 2 436 559 | /1 441 440 | ~1.69036 | |
| 17 | 42 142 223 | /24 504 480 | ~1.71978 | |
| 18 | 14 274 301 | /8 168 160 | ~1.74755 | |
| 19 | 275 295 799 | /155 195 040 | ~1.77387 | |
| 20 | 55 835 135 | /31 039 008 | ~1.79887 | |
| N | 최대 돌출부 | |||
|---|---|---|---|---|
| 분수로 표현된 | 십진법의 | 상대적 크기 | ||
| 21 | 18 858 053 | /10 346 336 | ~1.82268 | |
| 22 | 19 093 197 | /10 346 336 | ~1.84541 | |
| 23 | 444 316 699 | /237 965 728 | ~1.86715 | |
| 24 | 1 347 822 955 | /713 897 184 | ~1.88798 | |
| 25 | 34 052 522 467 | /17 847 429 600 | ~1.90798 | |
| 26 | 34 395 742 267 | /17 847 429 600 | ~1.92721 | |
| 27 | 312 536 252 003 | /160 626 866 400 | ~1.94573 | |
| 28 | 315 404 588 903 | /160 626 866 400 | ~1.96359 | |
| 29 | 9 227 046 511 387 | /4 658 179 125 600 | ~1.98083 | |
| 30 | 9 304 682 830 147 | /4 658 179 125 600 | ~1.99749 | |
테이블 가장자리를 지나 적어도 블록 길이에 도달하는 데 필요한 블록 수는 4, 31, 227, 1674, 12367, 91380, ...(OEIS에서 순차 A014537)이다.[1]
멀티 와이드
카운터 밸런싱을 사용하는 다중 폭 스택은 단일 폭 스택보다 더 큰 오버행(overhang)을 줄 수 있다.세 블록이라도 다른 블록 위에 균형잡힌 두 블록을 쌓으면 오버행(overhang)이 1인 반면, 단순 이상 사례의 오버행(overhang)은 기껏해야 1이다.11/12. 패터슨 외 연구원으로서. (2007) 점증상으로는 다중 폭 스택에 의해 달성될 수 있는 최대 오버행은 블록 수의 큐브 루트에 비례하는 것으로 나타났으며, 오버행은 블록 수의 로그에 비례하는 단일 폭의 경우와 대조적이다.그러나 실제로는 이것이 불가능하고 블록 응력으로 인해 오른쪽으로 이동할 수 있는 블록의 수가 지정된 수를 넘지 않는 것으로 나타났다.예를 들어, h = 0.20 m, 영의 계량 E = 3000 MPa 및 밀도 ρ = 1.8×103 kg/m3, 압축응력 3 MPa를 제한한 특수 벽돌의 경우, N의 대략적인 값은 853이고 최대 주탑 높이는 170 m가 된다.[2]
강건함
홀(2005)은 이 문제를 논의하고, 둥근 블록 모서리와 블록 배치의 유한 정밀도와 같은 비이상화에 강하다는 것을 보여주며, 인접한 블록들 사이의 비제로 마찰력을 포함한 여러 변형을 도입한다.
참조
- ^ Sloane, N. J. A. (ed.). "Sequence A014537 (Number of books required for n book-lengths of overhang in the harmonic book stacking problem.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Khoshbin-e-Khoshnazar, M. R. (2007). "Simplifying modelling can mislead students". Physics Education. 42: 14–15. doi:10.1088/0031-9120/42/1/F05.
- Hall, J. F. (2005). "Fun with stacking blocks". American Journal of Physics. 73 (12): 1107–1116. Bibcode:2005AmJPh..73.1107H. doi:10.1119/1.2074007..
- Johnson, Paul B. (April 1955). "Leaning Tower of Lire". American Journal of Physics. 23 (4): 240. Bibcode:1955AmJPh..23..240J. doi:10.1119/1.1933957.
- Paterson, Mike; Peres, Yuval; Thorup, Mikkel; Winkler, Peter; Zwick, Uri (2007). "Maximum overhang". arXiv:0707.0093 [math.HO].
외부 링크
- Weisstein, Eric W. "Book Stacking Problem". MathWorld.
- "Building an Infinite Bridge". PBS Infinite Series. 2017-05-04. Retrieved 2018-09-03.
 (와
(와