존슨 S-배급U

이 글은 통계 전문가의 주의가 필요하다. 구체적인 문제는 확률 분포에 대한 합리적인 표준에 대한 완성이다. Wiki Project Statistics가 전문가 영입에 도움을 줄 수 있을 것이다(2012년 11월)

존슨즈_U S

확률밀도함수
누적분포함수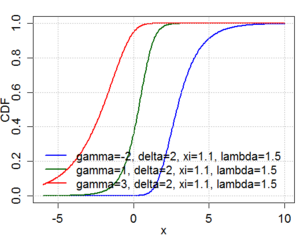
매개변수	> > ${\displaystyle \gamma,\xi,\deltada >0}$ (실제)
지원	${\displaystyle -\put{\text{{}}}$
PDF	${\displaystyle {\frac {\delta }{\lambda {\sqrt {2\pi }}}}{\frac {1}{\sqrt {1+\left({\frac {x-\xi }{\lambda }}\right)^{2}}}}e^{-{\frac {1}{2}}\left(\gamma +\delta \sinh ^{-1}\left({\frac {x-\xi }{\lambda }}\right)\right)^{2}}}$
CDF	${\displaystyle \Phi \왼쪽(\gamma +\delta \sinh ^{-1}\왼쪽({\frac {x-\xi }{\lambda }\오른쪽)}}$
평균	${\displaystyle \xi -\fractda \exp {\frac{-2}}:\sinh \left\frac{}}{\flict }}}$
중앙값	${\displaystyle \xi +\sinda \sinh \left {\frac {\fract }{\property }}}$
분산	${\displaystyle {\frac{\fracta ^{2}}:(\exp(\exp(\exp(\expect ^{-2})\cosh \left\frac {2\}{\frac }}}{\computer }\오른쪽)}}}}}}}}}}$

존슨의 S-분포는_U 1949년 N. L. 존슨이 처음 조사한 확률 분포의 4변수 계열이다.^[1][2] Johnson은 정규 분포의 변환으로 이것을 제안했다.^[1]

${\displaystyle z=\cHB +\sinh ^{-1}\왼쪽 사진\frac {x-\xi }{\exda }}\오른쪽)}$

${\displaystyle 여기}$서 $z{\displaystyle }$~ N${\displaystyle }$( ${\displaystyle 0,}$ ${\displaystyle 1}$) ${\displaystyle z\sim {\mathcal{N}(0,1$

랜덤 변수 생성

U를 단위 간격 [0, 1]에 균일하게 분포하는 랜덤 변수가 되게 한다. Johnson의 S_U 랜덤 변수는 다음과 같이 U에서 생성할 수 있다.

${\displaystyle x=\lambda \sinh \left({\frac {\Phi ^{-1}(U)-\gamma }{\delta }}\xi }$

여기서 φ은 정규 분포의 누적 분포 함수다.

존슨 S-배급_B

N. L. Johnson은^[1] 먼저 변환을 제안한다.

${\displaystyle z=\displaystyle z=\cHB +\\\frac {x-\xi }{\xi +\cHBDA -x}\오른쪽)}$

${\displaystyle 여기}$서 $z{\displaystyle }$~ N${\displaystyle }$( ${\displaystyle 0,}$ ${\displaystyle 1}$) ${\displaystyle z\sim {\mathcal{N}(0,1$

Johnson의 S_B 랜덤 변수는 다음과 같이 U에서 생성할 수 있다.

${\displaystyle y={\좌측(1+{e}^{-\좌측(z-\pair \우측)/\pair \우측)^{-1}$

${\displaystyle x=\data y+\xi }$

S-분포는_B 플라티쿠르틱 분포(카르토시스)가 편리하다. S를_U 시뮬레이션하기 위해, 밀도와 누적 밀도 함수에 대한 코드의 샘플을 여기에서 구할 수 있다.

적용들

존슨사의 $S{\displaystyle {}_{}}$ ${\displaystyle U_{}}$ ${\$ -분배가$$ 포트폴리오 관리를 위한 자산 수익률을 모델링하는 데 성공적으로 사용되었다.^[3] 존슨 분포는 관측된 변동성 미소를 수용하기 위해 옵션 가격 결정에도 종종 사용된다. 존슨 이항 트리를 참조한다.

Johnson 분포의 대안은 계량형 매개변수 분포(QPDs)이다. QPDs는 Johnson 시스템보다 더 큰 형상 유연성을 제공할 수 있다. QPD는 모멘트를 맞추는 대신 일반적으로 선형 최소 제곱이 있는 경험적 누적분포함수 데이터에 적합하다.

참조

추가 읽기

• Hill, I. D.; Hill, R.; Holder, R. L. (1976). "Algorithm AS 99: Fitting Johnson Curves by Moments". Journal of the Royal Statistical Society. Series C (Applied Statistics). 25 (2).
• Jones, M. C.; Pewsey, A. (2009). "Sinh-arcsinh distributions" (PDF). Biometrika. 96 (4): 761. doi:10.1093/biomet/asp053.(사전 인쇄)
• Tuenter, Hans J. H. (November 2001). "An algorithm to determine the parameters of S_U-curves in the Johnson system of probability distributions by moment matching". The Journal of Statistical Computation and Simulation. 70 (4): 325–347. doi:10.1080/00949650108812126.