지수적분

수학에서 지수 적분인 Ei는 복잡한 평면에서 특별한 함수다.그것은 지수함수와 그 인수 사이의 비율에 대한 하나의 특정한 확실한 적분으로 정의된다.

정의들

x의 실제 0이 아닌 값에 대해 지수 적분 Ei(x)는 다음과 같이 정의된다.

${\displaystyle \operatorname {Ei}(x)=-\int _{-x}^{-t}{t}\\\frac {e^{-t}}\{-\nt=\int _{-\frac}{x}{e^{t}}}\dt}\,dt},dt.}$

Risch 알고리즘은 Ei가 기본 함수가 아님을 보여준다.위의 정의는 x의 양의 값에 사용할 수 있지만, 통합의 특이성 및 0에 기인한 Cauchy 기본값의 측면에서 적분을 이해해야 한다.

인수의 복잡한 값의 경우, 지점 0과 $\infty {\displaystyle \mathrm{}}$ ${\displaystyle \infit }$에 따라 정의가 모호해진다.$$^[1]Ei 대신 다음과 같은 표기법을 사용한다.^[2]

${\displaystyle E_{1}(z)=\int _{z}^{\\inflt}{e^{-t}}}{\frac {e^{-t}}}\\\rqquad {\rm {Arg}(z) <\pi }}$

x의 ${\displaystyle 양}$의 값에 대해 -${\displaystyle {E\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$( x${\displaystyle }$)${\displaystyle }$= ${\displaystyle \mathrm{Ei}}$ ${\displaystyle }$(${\displaystyle }$- x${\displaystyle }$) ${\displaystyle -E_{1}(x)=\operatorname {Ei}(-x)}$이(가) 있다$.$

일반적으로 지점 절단은 음의 실제 축에 취하며 E는₁ 복잡한 평면의 다른 곳에 있는 분석적 연속에 의해 정의될 수 있다.

$z{\displaystyle }$ ${\displaystyle z}$의 실제 부분의 양의 값에 대해서는 이 값을 기록할^[3] 수 있다$.$

${\displaystyle E_{1}(z)=\int_{1}^{\inflac{e^{-tz}}{t}\,dt=\int_{0}^{0}1}{\frac {e^{-z/u}}}}{{u}}}\quad \Re(z)\geq 0}}$

분기 절단부 부근의 E의₁ 거동은 다음과 같은 관계로 볼 수 있다.^[4]

${\displaystyle \lim _{\delta \to 0+}E_{1}(-x\pm i\delta )=-\operatorname {Ei}(x)\mp i\pi ,\qquad x>0.}$

특성.

아래의 지수 적분 속성의 몇 가지 특성은, 특정한 경우에, 위 정의를 통한 명시적 평가를 피할 수 있다.

컨버전트 시리즈

음의 실제 축에서 벗어난 실제 또는 복잡한 ${\displaystyle {인수}_{}}$의 경우${\displaystyle {}_{}E}$1 ($$z ) {\$displaystyle E_{$1}($z)}$을(를) 다음과^[5] 같이 표현할 수 있다$$.

${\displaystyle E_{1}(z)=-\gamma -\ln z-\sum _{k=1}^{k=1}{\frac{(-z)^{k}}{k\;k!}}\qquad(\왼쪽 \operatorname {Arg}(z)\오른쪽 <\pi )}$

여기서 $\gamma {\displaystyle }$ ${\displaystyle \gamma}$은(는) 오일러-마스케로니 상수다.모든 복합 $z{\displaystyle }$ ${\displaystyle z$에 대한 합계가 수렴되며, 음의 실제 축을 따라 분기를 절단하는 복합 로그의 일반적인 값을 취한다.

이 공식은 0에서 2.5 사이의 $실제$ x ${\displaystyle$ x$}$에 대한 부동 소수점 연산을 사용하여$$ ${\displaystyle {E\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$( ${\displaystyle x}$) ${\displaystyle E_{1}(x)}$을 계산하는 데 사용할 수 있다.>.5 $[\displaystyle x >2.5$의 경우 취소로 인해 결과가 부정확하다.

라마누잔에 의해 더 빠른 융합 시리즈가 발견되었다.

${\displaystyle {\rm {Ei}}(x)=\gamma +\ln x+\exp {(x/2)}\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}x^{n}}{n!\,2^{n-1}}}\sum _{k=0}^{\lfloor (n-1)/2\rfloor }{\frac {1}{2k+1}}}$

이러한 교대 열은 작은 x에 대해 좋은 점증상 한계를 제공하는 데 사용될 수 있다.^{[citation needed]} 예:

${\displaystyle 1-{\frac{3x}{4}}\leq {\rm {Ei}-\ln x-{3x}{4}+{\frac{11x^{36}}}}}}}$

$x{\displaystyle }$ ${\displaystyle \ge }$ ${\displaystyle 0}$ ${\displaystyle x\geq$ 0$}$의 경우$.$

점근열

불행하게도, 위의 시리즈는 더 큰 계수의 논쟁에서 더디게 수렴된다.예를 들어 E ${\displaystyle {1\mathrm{}}_{}}$( ${\displaystyle 10}$) ${\displaystyle E_{1$}($10)}$에 대한 3개의 유의미한 숫자에 대한 정답을 맞추려면 40개 이상의 용어가 필요하다$.$^[6]단, x의 양의 값에 대해서는 x $e{\displaystyle }$ ${\displaystyle x^{}}$ ${\displaystyle E}$ ${\displaystyle {1\mathrm{}}_{}}$ (${\displaystyle {}_{}}$x )${\displaystyle xe^{x}E_{1}(x)}$을(를) 부품별로$$ 통합하여 얻을 수 있는 다이버전트 계열 근사치가 있다.^[7]

${\displaystyle E_{1}(x)={\frac {\exp(-x)}{x}}{n-1}{\frac {n!}{n}^{n}}}}+O(N!x^{-N})\right}$

$위$의 근사치의 상대적 오차는 N ${\displaystyle N}$의 다양한 값$,$ 잘린 합에 있는 항의 수(${\displaystyle }$${\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle N=1},$ $N{\displaystyle }$= ${\displaystyle 5}$ ${\displaystyle N=5},$ 분홍색$$)에 대해 오른쪽 그림에 표시된다.

지수 및 로그 동작: 브래킷링

이전 하위 절에서 제시된 두 시리즈로부터 E ${\displaystyle {1\mathrm{}}_{}}$ ${\$}는 인수의 큰 값에 대한 음수 지수처럼 작용하고$$ 작은 값에 대한 로그처럼 작용한다.인수의 양의 실제 값에 대해 E ${\displaystyle {1\mathrm{}}_{}}$ ${\$}은$($는) 다음과 같은 기본 함수로 분류할 수 있다$$.^[8]

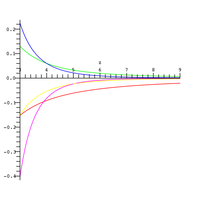
${\displaystyle {\frac{1}{2}}e^{-x}\,\ln \!\좌측(1+{\frac{2}{x}\오른쪽)E_{1}(x)<e^{-x}\,\ln \!\left(1+{\frac{1}{x}\오른쪽)\qquad x>0}$

이 불평등의 왼쪽은 파란색으로 왼쪽 그래프에 표시되며, $중앙부{\displaystyle {}_{}}$ ${\displaystyle {E\mathrm{}}_{}}$1 (${\displaystyle x}$ )$${\$displaystyle E_{1}(x)}$은 검은색으로 표시되고 오른쪽은 빨간색으로 표시된다.

아인별 정의

${\displaystyle \mathrm{Ei}}$ ${\displaystyle \operatorname {Ei} }$ $및{\displaystyle {}_{}}$ E$$$$ {\$displaystyle$E_{1} $모두$다음과 같이 정의된 전체$$^[9] 함수 ${\displaystyle \mathrm{Ein}}${\$displaysty \operatorname {Ein}$을(를) 사용하여 보다 간단하게 쓸 수 있다$$.

${\displaystyle \operatorname {Ein}=\int _{0}^{z}(1-e^{-t}){\frac {dt}{t}}}}}}}\sum _{k=1}^{k+1}z^{k\k\;k!}}}$

(이것은 위의 ${\displaystyle {\mathrm{}}_{}}$ 1$${\$displaystyle \mathrm{E$} $_{1$} 정의에서 교대 영상 시리즈일 뿐이라는 점에 유의하십시오.)$$그러면 우리는

${\displaystyle E_{1}(z)\,=\,-\gamma -\ln z+{\rm {Ein}}(z)\qquad \왼쪽 \operatorname {Arg}(z)\오른쪽 <\pi }$

${\displaystyle \operatorname {Ei}\(x)\,=\\gamma +\lnn {\좌측 x-\operatorname {Ein}(-x)\qquad x\neq 0}$

다른 기능과의 관계

쿠메르 방정식

${\displaystyle z{\frac {d^{2}w}{dz^{2}}+(b-z){\frac {dz}-aw=0}$

일반적으로 결합초기하함수 $M{\displaystyle }$(,${\displaystyle b}$, z${\displaystyle }$) ${\displaystyle M(a,b,z)}$ 및 $U$(, ${\displaystyle b,}$ ${\displaystyle z).}$ ${\displaystyle U(a,b,z$)에 의해 해결된다$.$$}$ 그러나$$ $a{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle a=0}$ 및 $b$ = ${\displaystyle 1,}${\$displaystyle b$=1$,}$일 때,

${\displaystyle z{\frac {d^{2}w}{dz^{2}}+(1-z){\frac {dz}=0}$

우리는 가지고 있다.

${\displaystyle M(0,1,z)=U(0,1,z)=1}$

모든 z에 걸쳐두₁ 번째 용액은 E(-z)에 의해 주어진다.실은.

${\displaystyle E_{1}(-z)=-\gamma -i\pi +{\frac [U(a,1,z)-M(a,1,z)]{\partial a},\partial a},\qquad 0<{\rm {Arg}(z)<2\pi }}$

$a{\displaystyle }$= ${\displaystyle 0.}$ ${\displaystyle a=0.}$ 결합초기하 함수와 다른$$ 연관성은 E가₁ 함수 U(1,1,z)의 지수 곱이라는 것이다.

${\displaystyle E_{1}(z)=e^{-z}U(1,1,z)}$

지수 적분은 공식에 의해 로그 적분 함수 li(x)와 밀접하게 관련되어 있다.

${\displaystyle \operatorname {li}(e^{x})=\operatorname {Ei}(x)}$

$x{\displaystyle }$ {\$displaystyle x}$의$$0이 아닌 실제 값의 경우

일반화

지수 적분 또한 다음과 같이 일반화될 수 있다.

${\displaystyle E_{n}(x)=\int _{1}^{\inflt }{e^{-xt}}{\frac {e^{-xt}}}}{t^{n}}}\,dt,}$

불완전한 감마 함수의 특별한 경우로 기록될 수 있다.^[10]

${\displaystyle E_{n}(x)=x^{n-1}\감마(1-n,x)}$

일반화된 형태는 Misra 함수^[11] ${\displaystyle {functionm}_{}}$(${\displaystyle x}$ ${\displaystyle )}$ ${\displaystyle \varphi _{m}(x)}$라고 부르기도 하는데$,$ 이는 다음과 같이 정의된다.

${\displaystyle \varphi _{m}(x)=E_{-m}(x).}$

이 일반화된 형태의 많은 특성들은 NIST 디지털 수학 기능 라이브러리에서 찾을 수 있다.

로그 포함은 일반화된 정수 함수를^[12] 정의함

${\displaystyle E_{s}^{j}(z)={\frac {1}{\감마(j+1)}}\int_{1}^{{1}{\inflt(\log t\오른쪽)^{j}{\frac{e^{-zt}}{t^{s}}\,dt.}$

무한 적분:

${\displaystyle \operatorname {Ei}(a\cdot b)=\iint e^{ab}\,da\,db}$

$d{\displaystyle (n}$) ${\displaystyle d(n)}$에 대한 일반 생성 함수$,$ $n{\displaystyle }$ ${\displaystyle n}$의 구분자 수$$:

${\displaystyle \sum \sum \n=1}d(n)x^{n}=\sum \d(n)x^}=\sum _{a=1}^{n1}\sum \sum \sum \sum \b=1}^{b=1}^{\x^{ab}}}}}}}}}}}}$

파생상품

$일반화함수{\displaystyle {}_{}}$ ${\displaystyle {En}_{}}${\$displaystyle E_{n}$의 파생상품은 공식으로 계산할 수 있다$$.

${\displaystyle E_{n}'(z)=-E_{n-1}(z)\qquad(n=1,2,3,\ldots )}$

$기능{\displaystyle {}_{}}$ ${\displaystyle {E\mathrm{}}_{}}$ 0$${\$displaystyle E_{0}$은(는) $e{\displaystyle {}^{}}$- ${\displaystyle z^{}}$/ ${\displaystyle z}$ ${\displaystyle e^{-z}/z}$에 불과하므로 평가하기가 쉽다는 점에 유의하십시오$.$^[14]

가상 인수의 지수적 적분

$z{\displaystyle }$ ${\displaystyle z}$이(가) 가상인$$ 경우 음이 아닌 실제 부분이 있으므로 공식을 사용할 수 있다.

${\displaystyle E_{1}(z)=\int _{1}^{\inflt }{\frac {e^{-tz}}{t}\,dt}$

삼각 통합 ${\displaystyle \mathrm{Si}}$ ${\displaystyle \operatorname {Si}$및$$ ${\displaystyle \mathrm{Ci}}$ ${\displaystyle \operatorname {Ci}$과(와) 관계를 얻으려면$:$

${\displaystyle E_{1}(ix)=i\왼쪽[-{\tfrac {1}{1}:{2}}\pi +\operatorname {Si}(x)\right]-\operatorname {Ci}(x)\qquad(x>0)}$

$E{\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {}_{}}$( ${\displaystyle i}$ ${\displaystyle x}$) ${\displaystyle \mathrm {E} _{1}(ix)}$의 실제 및 가상 부분은 검은색과 빨간색 곡선으로 오른쪽 그림에 표시된다$$.

근사치

지수 적분 함수에 대한 근사치가 여러 개 있었다.여기에는 다음이 포함된다.

• 스와메와 오히자 근사치^[15]
  $${\displaystyle E_{1}(x)=\왼쪽(A^{-7.7}+B\오른쪽)^{-0.13,}$$

  
  어디에
  $${\displaystyle {\reasoned}A&=\ln \left[\frac {0.56146}{x}+0.65\right)(1+x)\right]\\\B&=x^{4}e^{7.7x}(2+x)^{3.7}\end{정렬}}}}$$

  
• 앨런과 헤이스팅스 근사치
  $${\displaystyle E_{1}(x)={\begin{case}-\ln x+{\textbf {a}^{\displaysty}T}{\textbf{x}_{5},&x\leq 1\\\\\frac {e^{-x}}{x}}{\frac {{\textbf{b}^{{\frac}}}}{\frac {{\textbf{b}}^{{}}^{{}}}}T}{\textbf{x}_{3}{\textbf{c}^{T}{\textbf{x}_{3}},&x\geq 1\end{case}}}$$

  
  어디에
  $${\displaystyle {\required}{\textbf {a}&\dataq [-0.57722,0.99999,-0.24991,0.05519,-0.00976,0.00108]^{T}\\{\textbf{b}}&\triangleq [0.2677,8.63476,18.05902,8.57333]^{T}\\{\textbf {c}&\triangleq [3.95850,21.09965,25.63296,9.57332]^{T}\\{\textbf {x}_{k}&\triangleq [x^{0},x^{1},\dots,x^{k}]^{T}\end{aigned}}$$

  
• 지속적인 분수 팽창
  $${\displaystyle E_{1}(x)={\cfrac{e^{-x}{\cfrac{1}{1+{\cfrac{1}{{1+{\cfrac{2}{x+{\cfrac{3}}}}}}}}}}}}}}}}}}}{\cfrfrdddots{{-}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.}$$

  
• 배리 외 연구진의 ^[17]근사치
  $${\displaystyle E_{1}(x)={\frac {e^{-x}{1-g}}e^{-{-{\frac {x}{1-G}}}}}\ln \좌측[1+{\frac {g}{x}}-{1-{1-G}}{(h+bx)^}}}}}}}}}}}}}}}}}}오른쪽}}}}}}}}}}}}}}}}}}}}},$$

  
  여기서:
  $${\displaystyle {\begin{aligned}h&={\frac {1}{1+x{\sqrt {x}}}}+{\frac {h_{\infty }q}{1+q}}\\q&={\frac {20}{47}}x^{\sqrt {\frac {31}{26}}}\\h_{\infty }&={\frac {(1-G)(G^{2}-6G+12)}{3G(2-G)^{2}b}}\\b&={\sqrt {\frac {2(1-G)}{G(2-G)}}}\\G&=e^{-\gamma }\end{aligned}}}$$

  
  오일러-마스케로니 상수인 $\displaystyle \gamma }$을(를) 사용하여.

적용들

• 시간에 따른 열전달
• Teis 용액 내 불균형 지하수 흐름(우물함수라고 함)
• 항성 및 행성 대기에서의 복사 전달
• 선원과 싱크대를 이용한 과도상태 또는 비정상상태 유동에 대한 방사형 확산 방정식
• 단순화된 1-D 기하학적^[18] 구조의 중성자 전달 방정식에 대한 솔루션

참고 항목

• Goodwin-Staton 적분
• 비클리-나일러 함수

메모들

참조

• Abramowitz, Milton; Irene Stegun (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Abramowitz and Stegun. New York: Dover. ISBN 978-0-486-61272-0., 5장.
• Bender, Carl M.; Steven A. Orszag (1978). Advanced mathematical methods for scientists and engineers. McGraw–Hill. ISBN 978-0-07-004452-4.
• Bleistein, Norman; Richard A. Handelsman (1986). Asymptotic Expansions of Integrals. Dover. ISBN 978-0-486-65082-1.
• Busbridge, Ida W. (1950). "On the integro-exponential function and the evaluation of some integrals involving it". Quart. J. Math. (Oxford). 1 (1): 176–184. Bibcode:1950QJMat...1..176B. doi:10.1093/qmath/1.1.176.
• Stankiewicz, A. (1968). "Tables of the integro-exponential functions". Acta Astronomica. 18: 289. Bibcode:1968AcA....18..289S.
• Sharma, R. R.; Zohuri, Bahman (1977). "A general method for an accurate evaluation of exponential integrals E₁(x), x>0". J. Comput. Phys. 25 (2): 199–204. Bibcode:1977JCoPh..25..199S. doi:10.1016/0021-9991(77)90022-5.
• Kölbig, K. S. (1983). "On the integral exp(−μt)t^ν−1log^mt dt". Math. Comput. 41 (163): 171–182. doi:10.1090/S0025-5718-1983-0701632-1.
• Milgram, M. S. (1985). "The generalized integro-exponential function". Mathematics of Computation. 44 (170): 443–458. doi:10.1090/S0025-5718-1985-0777276-4. JSTOR 2007964. MR 0777276.
• Misra, Rama Dhar; Born, M. (1940). "On the Stability of Crystal Lattices. II". Mathematical Proceedings of the Cambridge Philosophical Society. 36 (2): 173. Bibcode:1940PCPS...36..173M. doi:10.1017/S030500410001714X.
• Chiccoli, C.; Lorenzutta, S.; Maino, G. (1988). "On the evaluation of generalized exponential integrals E_ν(x)". J. Comput. Phys. 78 (2): 278–287. Bibcode:1988JCoPh..78..278C. doi:10.1016/0021-9991(88)90050-2.
• Chiccoli, C.; Lorenzutta, S.; Maino, G. (1990). "Recent results for generalized exponential integrals". Computer Math. Applic. 19 (5): 21–29. doi:10.1016/0898-1221(90)90098-5.
• MacLeod, Allan J. (2002). "The efficient computation of some generalised exponential integrals". J. Comput. Appl. Math. 148 (2): 363–374. Bibcode:2002JCoAm.138..363M. doi:10.1016/S0377-0427(02)00556-3.
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 6.3. Exponential Integrals", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
• Temme, N. M. (2010), "Exponential, Logarithmic, Sine, and Cosine Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248

외부 링크

• "Integral exponential function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• 일반화 지수 통합에 대한 NIST 문서
• Weisstein, Eric W. "Exponential Integral". MathWorld.
• Weisstein, Eric W. "En-Function". MathWorld.
• "Exponential integral Ei". Wolfram Functions Site.
• 지수, 로그, 사인 및 코사인 통합(DLMF)