스펙트럼 밀도 추정

통계 신호 처리에서 스펙트럼 밀도 추정(SDE) 또는 단순히 스펙트럼 추정의 목적은 신호의 ^[1]시간 샘플 시퀀스에서 랜덤 신호의 스펙트럼 밀도(파워 스펙트럼 밀도라고도 함)를 추정하는 것이다.직관적으로 말하면, 스펙트럼 밀도는 신호의 주파수 내용을 특징짓습니다.스펙트럼 밀도를 추정하는 한 가지 목적은 이러한 주기성에 해당하는 주파수에서 피크를 관찰함으로써 데이터의 주기성을 검출하는 것이다.

일부 SDE 기술에서는 신호가 제한된 수의 발생 주파수와 노이즈로 구성되어 있다고 가정하고 생성된 주파수의 위치와 강도를 찾습니다.다른 사람들은 구성요소의 수를 가정하지 않고 전체 생성 스펙트럼을 추정하려고 한다.

개요

음성 파형과 그 주파수 스펙트럼의 예

220Hz에서 "기본" 주파수에 이어 220Hz의 배수(조파)를 나타내는 주기적 파형(삼각파) 및 주파수 스펙트럼.

음악 세그먼트의 전력 스펙트럼 밀도는 비교를 위해 두 가지 다른 방법으로 추정됩니다.

주파수 영역 분석 또는 스펙트럼 밀도 추정이라고도 하는 스펙트럼 분석은 복잡한 신호를 더 단순한 부분으로 분해하는 기술적 과정이다.위에서 설명한 바와 같이, 많은 물리적 프로세스는 많은 개별 주파수 구성요소의 합으로 가장 잘 설명됩니다.다양한 양(예: 진폭, 전력, 강도) 대 주파수(또는 위상)를 정량화하는 모든 프로세스를 스펙트럼 분석이라고 할 수 있다.

신호 전체에 대해 스펙트럼 분석을 수행할 수 있습니다.또는 신호를 짧은 세그먼트(프레임이라고도 함)로 분할하여 스펙트럼 분석을 이러한 개별 세그먼트에 적용할 수 있습니다.정기 함수( $\sin(t)$ : sin $\sin(t)$ ( t ) \ $displaystyle \sin$ ( $t$ ) )는 이 서브디비전에 특히 적합합니다.비주기 함수를 분석하기 위한 일반적인 수학적 기법은 푸리에 분석의 범주에 속합니다.

함수의 푸리에 변환은 원래 신호에 대한 모든 정보를 포함하지만 다른 형태로 주파수 스펙트럼을 생성합니다.즉, 원래 함수는 역 푸리에 변환을 통해 완전히 재구성(합성)될 수 있습니다.완벽한 재구성을 위해 스펙트럼 분석기는 각 주파수 성분의 진폭과 위상을 모두 보존해야 합니다.이 두 가지 정보는 2차원 벡터, 복소수 또는 극좌표에서의 크기(진폭) 및 위상(즉, 위상)으로 표현될 수 있다.신호 처리의 일반적인 기술은 제곱 진폭 또는 전력을 고려하는 것입니다. 이 경우 결과 그래프를 전력 스펙트럼이라고 합니다.

가역성 때문에 푸리에 변환은 시간이 아닌 주파수로 함수의 표현이라고 불리며, 따라서 주파수 영역 표현입니다.시간 영역에서 수행할 수 있는 선형 연산에는 주파수 영역에서 더 쉽게 수행할 수 있는 대응 연산이 있습니다.또한 주파수 분석을 통해 선형 및 비선형 모두 다양한 시간 영역 연산의 효과를 이해하고 해석할 수 있습니다.예를 들어, 비선형 또는 시간 가변 연산만이 주파수 스펙트럼에 새로운 주파수를 생성할 수 있습니다.

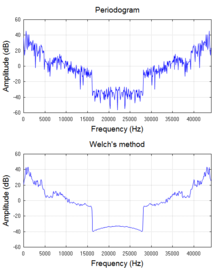
실제로 주파수 스펙트럼을 생성하는 거의 모든 소프트웨어 및 전자 디바이스는 신호의 샘플로 동작하며 완전한 적분 솔루션에 대한 수학적 근사치를 제공하는 이산 푸리에 변환(DFT)을 사용합니다.DFT는 거의 항상 Fast Fourier Transform(FFT; 고속 푸리에 변환)이라고 불리는 효율적인 알고리즘에 의해 구현됩니다.DFT의 제곱 크기 성분 배열은 주기율이라고 불리는 전력 스펙트럼의 일종으로 필터 임펄스 응답 및 창 기능 등 노이즈 없는 기능의 주파수 특성을 조사하는 데 널리 사용된다.그러나 주기율표는 낮은 신호 대 잡음비의 노이즈 신호 또는 사인파에 적용할 경우 처리 이득을 제공하지 않습니다.즉, 주어진 주파수에서 스펙트럼 추정의 분산은 계산에 사용된 샘플의 수가 증가하더라도 감소하지 않는다.이는 시간 경과에 따른 평균화(Welch의 방법^[2]) 또는 주파수 초과(스무징)를 통해 완화될 수 있습니다.Welch의 방법은 스펙트럼 밀도 추정(SDE)에 널리 사용된다.그러나 주기율 기반 기법은 일부 애플리케이션에서 허용되지 않는 작은 편견을 도입한다.그래서 다음 섹션에서는 다른 대안을 제시합니다.

기술

스펙트럼 추정을 위한 다른 많은 기법이 기본 주기율의 단점을 완화하기 위해 개발되었다.이러한 기술은 일반적으로 비파라미터, 파라메트릭 및 최근에는 반파라메트릭(^[3]스퍼스라고도 함) 방식으로 나눌 수 있습니다.비모수적 접근법은 공정이 특정 구조를 가지고 있다고 가정하지 않고 공분산 또는 공정의 스펙트럼을 명시적으로 추정합니다.기본 애플리케이션에 사용되는 가장 일반적인 추정기(예: 웰치의 방법) 중 일부는 주기도와 밀접하게 관련된 비모수 추정기이다.대조적으로, 파라메트릭 접근법은 기초가 되는 고정 확률적 과정이 소수의 파라메타를 사용하여 설명할 수 있는 특정 구조를 가지고 있다고 가정한다(예를 들어, 자동 회귀 또는 이동 평균 모델을 사용).이러한 접근법에서 과제는 확률적 과정을 설명하는 모델의 매개변수를 추정하는 것이다.반모수적 방법을 사용할 때, 기본 프로세스는 비모수적 프레임워크를 사용하여 모델링되며, 모델의 0이 아닌 구성요소의 수가 작다는 추가 가정(즉, 모델이 희박하다)이 있다.신호 재구성뿐만 아니라 누락 데이터 복구에도 유사한 접근방식을 사용할 수 있습니다.

다음은 비모수 스펙트럼 밀도 추정 기법의 일부 목록입니다.

주기율, 이산 푸리에 변환의 계수 제곱
바틀렛의 방법은 스펙트럼 밀도 추정의 분산을 줄이기 위해 신호의 여러 세그먼트에 대해 취한 주기그램의 평균이다.
Welch's 메서드는 겹치는 세그먼트를 사용하는 Bartlett 메서드의 윈도우 버전입니다.
멀티페이퍼는 스펙트럼 밀도 추정의 분산을 줄이기 위해 스펙트럼 밀도의 독립적인 추정치를 형성하기 위해 여러 테이퍼 또는 창을 사용하는 주기율 기반 방법이다.
알려진 주파수에 적합한 최소 제곱을 기반으로 하는 최소 제곱 스펙트럼 분석
신호 샘플의 간격이 일정하지 않은 경우 불균일한 이산 푸리에 변환이 사용됩니다.
특이 스펙트럼 분석은 공분산 행렬의 특이값 분해를 사용하여 스펙트럼 밀도를 추정하는 비모수적 방법이다.
단시간 푸리에 변환
임계 필터는 노이즈, 불완전한 데이터 및 계측 응답 함수를 처리할 수 있는 정보 필드 이론에 기초한 비모수적 방법입니다.

파라미터 기술의 일부를 다음에 나타냅니다.

자기 회귀 모형(AR) 추정 - n번째 표본이 이전 p 표본과 상관 관계가 있다고 가정합니다.
이동 평균 모델(MA) 추정 - n번째 표본이 이전 p 표본의 노이즈 항과 상관 관계가 있다고 가정합니다.
AR 및 MA 모형을 일반화하는 자동 회귀 이동 평균(ARMA) 추정입니다.
MUSIC(Multiple SIGnal Classification)은 널리 사용되는 슈퍼 해상도 방법입니다.
최대 엔트로피 스펙트럼 추정은 첨예한 피크와 같은 단수 스펙트럼 특징이 예상되는 경우 SDE에 유용한 올폴 방법이다.

마지막으로 반파라미터 기술의 몇 가지 예를 제시하겠습니다.

SPICE(^[3]SParse Repeative Distribution-Based Estimation) 추정 및 보다 $(r,q)$ 일반화된 ( $(r,q)$ q $)$ \ $displaystyle (r,q)}$ - SPICE. $(r,q)$ ^[5]
반복적 적응적 접근법(IAA) 추정.^[6]
Lasso, 최소 제곱 스펙트럼 분석과 유사하지만 희소성 적용 패널티.^[7]

모수 추정

파라메트릭 스펙트럼 추정에서는 신호가 스펙트럼 밀도 함수(SDF) $(f$ $S(f;a_{1},\ldots ,a_{p})$ $S(f;a_{1},\ldots ,a_{p})$ $S(f;a_{1},\ldots ,a_{p})$ , $S(f;a_{1},\ldots ,a_{p})$ )({ $f;a_{1},\ldots,a_{p})$ 를 $S(f;a_{1},\ldots ,a_{p})$ 갖는 고정 프로세스에 의해 모델링된다고 가정합니다 $a_{1},\ldots ,a_{p}$ 은 주파수 $f$ { $displaystyle$ f $}$ 및 $f$ ${$ p} $파라미터$ 의 $a_{1},\ldots ,a_{p}$ 입니다 $p$ $a_{1},\ldots ,a_{p}$ $\$ ^[8]그러면 추정 문제가 이러한 모수를 추정하는 문제가 됩니다.

모수 SDF 추정의 가장 일반적인 형태는 자기 회귀 ${\text{AR}}(p)$ AR $)$ 을 모델로 사용한다.\style $\text{$ $AR}}(p)$ 의 ${\text{AR}}(p)$ 순서 p ${displaystyle$ p $p$ ^[8]^{: 392} 0 ${\text{AR}}(p)$ AR $)$ 에 따르는 $\{Y_{t}\}$ 신호 시퀀스 $\{Y_{t}\}$ { $\{Y_{t}\}$ t $\{Y_{t}\}$ }({ $Y_{t}\})$ {displaystyle\text $}($ ) $AR}}(p)}$ 프로세스가 ${\text{AR}}(p)$ 방정식을 만족합니다.

\displaystyle Y_{t}=\phi _{1}Y_{t-1}+\phi _{2}Y_{t-2}+\cdots +\phi _{p}Y_{t-p}+\epsilon _{t}}

$\phi _{1},\ldots ,\phi _{p}$ 서 § $\phi _{1},\ldots ,\phi _{p}$ 1, $\phi _{1},\ldots ,\phi _{p}$ § $\phi _{1},\ldots ,\phi _{p}$ \ $displaystyle \phi$ _ ${1},\ldots,\phi$ _{ $p}$ 는 $\phi _{1},\ldots ,\phi _{p}$ 고정계수이고 § $\epsilon _{t}$ \ $displaystyle \silon$ _ ${$ $t}$ 는 $\epsilon _{t}$ 평균과 혁신변화가 제로인 화이트노이즈 $\sigma _{p}^{2}$ 입니다 § $\sigma _{p}^{2}$ { $displaystyle \p}^{2$ 이 프로세스의 SDF는

{\displaystyle S(f;\phi _{1},\ldots,\phi _{p},\delta_{p}^{2}={\left 1-sum _{k=1}^{p}\phi _{k}e^{-2\pi fk\Delta}}^{}}}}오른쪽

샘플링 시간 간격은 $δ$ t {\ $displaystyle$ \ $Delta$ $f_{N}$ $}$ 이고 나이키스트 주파수 f_{N $f_{N}$ }는 f N $f_{N}$ { $displaystyle$ f_ ${N$ }입니다.

${\text{AR}}(p)$ p ${\text{AR}}(p)$ )의 $\phi _{1},\ldots ,\phi _{p},\sigma _{p}^{2}$ $\phi _{1},\ldots ,\phi _{p},\sigma _{p}^{2}$ 1 $\phi _{1},\ldots ,\phi _{p},\sigma _{p}^{2}$ $\phi _{1},\ldots ,\phi _{p},\sigma _{p}^{2}$ $\phi _{1},\ldots ,\phi _{p},\sigma _{p}^{2}$ p2 {\ $\phi _{1},\ldots ,\phi _{p},\sigma _{p}^{2}$ \ $phi _{1},\ldots,\sigma$ _ ${p$ }^ $2}$ 에는 $\phi _{1},\ldots ,\phi _{p},\sigma _{p}^{2}$ 다수의 $접근법$ 이 $있습니다.$ $AR}}(p)}$ 프로세스와 ${\text{AR}}(p)$ 그에 따른 ^[8]^{: 452-453}스펙트럼 밀도:

Yule-Walker 추정치는 AR $(\$ displaystyle\text)에 ${\text{AR}}(p)$ Yule-Walker 방정식을 재귀적으로 풀어서 찾을 수 $있습니다.$ $AR}}($ p $)}$ 프로세스
Burg 추정기는 Yule-Walker 방정식을 일반적인 최소 제곱 문제의 한 형태로 처리함으로써 찾을 수 있다.Burg 추정치는 일반적으로 Yule-Walker ^[8]^{: 452}추정치보다 우수한 것으로 간주됩니다.Burg는 이를 최대 엔트로피 스펙트럼 ^[9]추정과 연관시켰다.
전방-후방 최소 제곱 추정기는 AR ${\text{AR}}(p)$ ${\text{AR}}(p)$ ) ${\text{AR}}(p)$ { $displaystyle$ {text $}$ 를 처리합니다. $AR}}(p)}$ 은 ${\text{AR}}(p)$ (는) 회귀 문제로 처리되며, 포워드-백워드 방식을 사용하여 문제를 해결합니다.그들은 Burg의 추정치와 경쟁적이다.
최대우도 추정기는 최대우도 접근법을 사용하여 모수를 추정합니다.여기에는 비선형 최적화가 수반되며 처음 세 가지보다 더 복잡합니다.

대체 파라메트릭 방법으로는 이동평균모델(MA) 및 완전 자기회귀 이동평균모델(ARMA)에 적합하는 방법이 있습니다.

주파수 추정

주파수 추정은 ^[10]성분의 수에 대한 가정이 주어졌을 때 노이즈가 존재하는 신호의 복잡한 주파수 성분을 추정하는 과정입니다.이는 구성요소에 대한 사전 가정을 하지 않는 위의 일반적인 방법과 대조됩니다.

싱글톤

가장 큰 단일 주파수만 추정하려면 피치 검출 알고리즘을 사용할 수 있습니다.지배적인 주파수가 시간에 따라 변화할 경우 문제는 시간-주파수 표현에서 정의된 순간 주파수의 추정이 됩니다.순간 주파수 추정 방법에는 위그너-빌 분포 및 고차 모호성 ^[11]함수에 기초한 방법이 포함된다.

수신 신호의 모든(복잡할 가능성이 있는) 주파수 성분(전송 신호 및 노이즈 포함)을 알고 싶다면 멀티 톤 방식을 사용합니다.

멀티톤

$x(n)$ x ( $x(n)$ ) $x(n)$ { $displaystyle$ x $(n)}$ 의 $x(n)$ 일반적인 모델은 백색 노이즈가 존재하는 경우 p{ $displaystyle$ p $}$ 의 $p$ $복잡한$ 지수 합계로 구성됩니다 $w(n)$ ( $w(n)$ ) $w(n)$ { $displaystyle$ w ( $n$ ) }

display

}A_{

i}

e^{jn\omega_{i}}+w

n

)}.

x $x(n)$ ( $x(n)$ ) $x(n)$ { $displaystyle$ x $(n)}$ 의 $x(n)$ 전력 스펙트럼 밀도는 노이즈에 의한 스펙트럼 밀도 함수와 더불어p { $displaystyle$ p $}$ 임펄스 함수로 $p$ 됩니다.

주파수 추정을 위한 가장 일반적인 방법에는 이러한 성분을 추출하기 위한 소음 부분 공간을 식별하는 것이 포함됩니다.이러한 방법은 자기 상관 행렬의 고유 분해를 신호 부분 공간과 노이즈 부분 공간으로 기반으로 합니다.이들 서브스페이스가 식별된 후 주파수 추정 함수를 사용하여 노이즈 서브스페이스로부터의 성분 주파수를 구한다.노이즈 부분 공간 기반 주파수 추정의 가장 일반적인 방법은 피사렌코의 방법, 다중 신호 분류(MUSIC) 방법, 고유 벡터 방법 및 최소 노름 방법입니다.

피사렌코의 방법: ${P}}_{\text}PHD}}\left(e^{j\omega}\right)=param frac {1}{\left \mathbf {e}^{H}\mathbf {v}_{\text{min}}\right ^{2}}}}$
음악: ${\hat {P}}_{\text{MU}}\left(e^{j\omega }\right)={\frac {1}{\sum _{i=p+1}^{M}\left|\mathbf {e} ^{H}\mathbf {v} _{i}\right|^{2}}}$ $MU}}\left(e^{j\omega}\오른쪽)=pfrac {1}{\sum _{i=p+1}^{$ $M}\left \mathbf {e}^{H}\mathbf {v}_{i}\right$ ^{ $2$
고유벡터법: ${P}}_{\text}EV}}\left(e^{j\omega}\오른쪽)=sum frac {1}{\sum _{i=p+1}^{M}{\frac {1}{\lambda _{i}}\left \mathbf {e}^{H}\mathbf {v}_{i}\right ^{2}}}$
최소 규범법: ${P}}_{\text}MN}}\left(e^{j\omega}\right)=param frac {1}{\left \mathbf {e}^{H}\mathbf {a}\right ^{2};\parambf {a} =\parambf {P} _{n} \mathbf {1$

계산 예시

$x_{n}$ n(\ $displaystyle x_{n$ n $n=0$ (\ $displaystyle$ n $=0$ ~ $N-1$ - $N-1$ (\ $displaystyle N-1)$ 의 $N-1$ 평균이 0인 시계열(표준 시간)이라고 $x_{n}$ 합니다.한정된 수의 주기적 성분의 합이라고 가정합니다(모든 주파수는 양수입니다).

{\displaystyle}{displaystyle}x_{n}&=\sum _{k}A_{k}\sin(2\pi \nu _{k}n+\phi _{k}\&=\sum _{k})A_{k}\left(\sin(\phi _{k})\cos(2\pi \nu _{k}n)+\cos(\phi _{k}n)\sin(2\pi \nu _{k}n)\right)\\&=\sum _{k}\left(\overbrace {a_{k})^{A_{k}\sin(\phi_{k})}\cos(2\pi \nu _{k}n)+\overbrace {b_{k}\cos(\phi_k})\cos(\n)_{k} \cos(\nu}_{k}\n}

$x_{n}$ n(\ $displaystyle x_{n})$ 의 $x_{n}$ 분산은 위와 같이 0-평균 함수의 경우 다음과 같습니다.

{{displaystyle {frac {1}{N}}\sum _{n=0}^{N-1}x_{n}^2}.}

이러한 데이터가 전기 신호에서 추출한 샘플일 경우, 평균 전력입니다(전력은 단위 시간당 에너지이므로 에너지가 진폭 제곱과 유사한 경우 분산과 유사합니다).

단순화를 위해 신호가 시간 내에 무한히 확장되므로 N $N\to \infty .$ $N\to \infty .$ . $N\to \infty .$ \ $displaystyle$ N \ $to \infty$ . $N\to \infty .$ } $N\to \infty .$ 전력이 제한되면 다음과 같은 제한이 존재하며 데이터의 분산입니다.

\lim _{N\to\infty}{\frac {1}{N}\sum _{n=0}^{N-1}x_{n}^2}.

다시 한 번 간단하게 하기 위해 연속적인 시간으로 넘어가고 신호가 양방향으로 무한히 연장된다고 가정합니다.그러면 이 두 공식은

x(t)=\sum _{k}A_{k}\sin(2\pi \nu _{k}t+\phi _{k}}

그리고.

\displaystyle \lim _{T\to\infty}{\frac {1}{2T}}\int _{-T}^{T}x(t)^{2}dt.}

$sin의$ 평균 $제곱$ 은 $1/{\sqrt {2}}$ / $({$ 1 $/{\sqrt {2$ 이므로 $A_{k}\sin(2\pi \nu _{k}t+\phi _{k})$ $A_{k}\sin(2\pi \nu _{k}t+\phi _{k})$ {\ ( $A_{k}\sin(2\pi \nu _{k}t+\phi _{k})$ {\ $A_{k}\sin(2\pi \nu _{k}t+\phi _{k})$ t + $A_{k}\sin(2\pi \nu _{k}t+\phi _{k})$ ){ ${\tfrac {1}{2}}A_{k}^{2}.$ A _ { k $\sin$ $}$ \ $sin ( 2$ \ $pi$ \ $nu$ _ { $k$ $}$ + \ $phi _ k$ } )의 분산은 ${\tfrac {1}{2}}A_{k}^{2}.$ ({ k style $)입니다$ } 따라서 ${\tfrac {1}{2}}A_{k}^{2}.$ $\nu _{k}$ 가 $\nu _{k}$ ({ $displaystyle$ $\nu_{$ k $\nu _{k}$ ${\tfrac {1}{2}}A_{k}^{2}.$ 인 컴포넌트에서 $x(t)$ x $({displaystyle x($ t $x(t)$ )})의 $x(t)$ 평균 $x(t)$ 에 대한 기여도는 $12A입니다.{displaystyle$ {1 $}{2$ }} $A_{k}^$ 2}. 이 ${\tfrac {1}{2}}A_{k}^{2}.$ 모든 기여는 $($ 의 $x(t).$ 평균 $x(t).$ 에 해당합니다. $}$

그러면 주파수의 함수로써의 검정력은 1 ${\tfrac {1}{2}}A_{k}^{2},$ ${\tfrac {1}{2}}A_{k}^{2},$ 2 , ${\tfrac {1}{2}}A_{k}^{2},$ {\ $displaystyle {1}{2}A_{k}^2$ } 이며 ${\tfrac {1}{2}}A_{k}^{2},$ , 통계적 $S(\nu )$ ( $S(\nu )$ ) {\ $displaystyle$ S ( \ $nu$ )는 $S(\nu )$ 다음과 같습니다.

S(\nu)=\sum _{k:\nu _{k}<\nu}{\frac {1}{2}A_{k}^2}.

$(\displaystyle$ S $)$ 는 $S$ 단조롭게 감소하지 않는 스텝 함수입니다.점프는 x $(\displaystyle$ x $x$ 의 주기적 구성요소의 주파수에서 발생하며, 각 점프 값은 해당 구성요소의 검정력 또는 분산입니다.

분산은 데이터 자체와의 공분산입니다.동일한 데이터를 고려하지만 지연이 $\tau$ { $displaystyle$ \ $tau$ 인 경우 $x(t)$ x $x(t)$ ( $x(t)$ ) $x(t+\tau )$ { $displaystyle$ x $($ t + $x(t+\tau )$ ) { $displaystyle$ x ( $t+\tau$ 와 $x(t+\tau )$ ( $x(t+\tau )$ + $x(t+\tau )$ } 의 공분산을 취하여 이를 신호 $(또는$ displaystylex $x$ 의 $자기상관함수$ c {\ $displaystyle$ c $}$ 로 $c$ 정의할 수 있습니다.

\displaystyle c(\displaystyle)=\lim _{T\to\infty}{\frac {1}{2T}}\int _{-T}^{T}x(t)x(t+\tau)dt.}

존재하는 경우 $\tau .$ 의 짝수 함수입니다 $.평균$ 전력이 한정되어 있는 $경우$ c $\displaystyle$ c는 $c$ 어디에나 존재하고 유한하며 c $c(0),$ ( $c(0),$ $),$ c (\ $displaystyle$ c $c(0),$ $(0)$ 로 한정되어 있습니다.c는 데이터의 평균 전력 또는 분산입니다 $.$

c{\ $displaystyle$ c $}$ 는 $c$ x {\ $displaystyle$ x $x$ 와 같은 주기의 주기적인 성분으로 분해할 수 $있습니다$ .

c(\displaystyle)=\sum _{k}{2}A_{k}^{2}\cos(2\pi \nu _{k}\display)

이는 실제로 여러 주파수에 걸친 c ${displaystyle$ c $}$ 의 $c$ 스펙트럼 분해로 주파수에 대한 x ${displaystyle$ x $}$ 의 $x$ $전력$ 분포와 관련이 있습니다. c ${displaystyle$ c $}$ 의 $c$ 주파수 성분의 진폭은 신호의 평균 전력에 기여합니다.

이 예의 전력 스펙트럼은 연속적이지 않기 때문에 도함수가 없기 때문에 이 신호에는 전력 스펙트럼 밀도 함수가 없습니다.일반적으로 전력 스펙트럼은 두 부분의 합이 된다. 이 예에서는 연속적이지 않고 밀도 함수를 가지지 않는 라인 스펙트럼과 절대 연속적이며 밀도 함수를 가지지 않는 잔류물이다.

「」를 참조해 주세요.

레퍼런스

^ P Stoica와 R Moses, 신호 스펙트럼 분석, 프렌티스 홀, 2005.
^ Welch, P. D. (1967), "The use of Fast Fourier Transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms", IEEE Transactions on Audio and Electroacoustics, AU-15 (2): 70–73, Bibcode:1967ITAE...15...70W, doi:10.1109/TAU.1967.1161901
^ ^a ^b Stoica, Petre; Babu, Prabhu; Li, Jian (January 2011). "New Method of Sparse Parameter Estimation in Separable Models and Its Use for Spectral Analysis of Irregularly Sampled Data". IEEE Transactions on Signal Processing. 59 (1): 35–47. Bibcode:2011ITSP...59...35S. doi:10.1109/TSP.2010.2086452. ISSN 1053-587X. S2CID 15936187.
^ Stoica, Petre; Li, Jian; Ling, Jun; Cheng, Yubo (April 2009). "Missing data recovery via a nonparametric iterative adaptive approach". 2009 IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE: 3369–3372. doi:10.1109/icassp.2009.4960347. ISBN 978-1-4244-2353-8.
^ Sward, Johan; Adalbjornsson, Stefan Ingi; Jakobsson, Andreas (March 2017). "A generalization of the sparse iterative covariance-based estimator". 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE: 3954–3958. doi:10.1109/icassp.2017.7952898. ISBN 978-1-5090-4117-6. S2CID 5640068.
^ Yardibi, Tarik; Li, Jian; Stoica, Petre; Xue, Ming; Baggeroer, Arthur B. (January 2010). "Source Localization and Sensing: A Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares". IEEE Transactions on Aerospace and Electronic Systems. 46 (1): 425–443. Bibcode:2010ITAES..46..425Y. doi:10.1109/TAES.2010.5417172. hdl:1721.1/59588. ISSN 0018-9251. S2CID 18834345.
^ Panahi, Ashkan; Viberg, Mats (February 2011). "On the resolution of The LASSO-based DOA estimation method". 2011 International ITG Workshop on Smart Antennas. IEEE: 1–5. doi:10.1109/wsa.2011.5741938. ISBN 978-1-61284-075-8. S2CID 7013162.
^ ^a ^b ^c ^d Percival, Donald B.; Walden, Andrew T. (1992). Spectral Analysis for Physical Applications. Cambridge University Press. ISBN 9780521435413.
^ Burg, J.P.(1967) "최대 엔트로피 스펙트럼 분석", 오클라호마주 오클라호마시티 탐사 지구물리학회 제37차 회의 진행.
^ Hayes, Monson H., Statistical Digital Signal Processing and Modeling, John Wiley & Sons, Inc., 1996.ISBN 0-471-59431-8.
^ Lerga, Jonatan. "Overview of Signal Instantaneous Frequency Estimation Methods" (PDF). University of Rijeka. Retrieved 22 March 2014.

추가 정보

Porat, B. (1994). Digital Processing of Random Signals: Theory & Methods. Prentice Hall. ISBN 978-0-13-063751-2.
Priestley, M.B. (1991). Spectral Analysis and Time Series. Academic Press. ISBN 978-0-12-564922-3.

Stoica, P.; Moses, R. (2005). Spectral Analysis of Signals. Prentice Hall. ISBN 978-0-13-113956-5.

Thomson, D. J. (1982). "Spectrum estimation and harmonic analysis". Proceedings of the IEEE. 70 (9): 1055–1096. Bibcode:1982IEEEP..70.1055T. CiteSeerX 10.1.1.471.1278. doi:10.1109/PROC.1982.12433. S2CID 290772.

[1] P Stoica와 R Moses, 신호 스펙트럼 분석, 프렌티스 홀, 2005.

[2] Welch, P. D. (1967), "The use of Fast Fourier Transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms", IEEE Transactions on Audio and Electroacoustics, AU-15 (2): 70–73, Bibcode:1967ITAE...15...70W, doi:10.1109/TAU.1967.1161901

[:0-3] Stoica, Petre; Babu, Prabhu; Li, Jian (January 2011). "New Method of Sparse Parameter Estimation in Separable Models and Its Use for Spectral Analysis of Irregularly Sampled Data". IEEE Transactions on Signal Processing. 59 (1): 35–47. Bibcode:2011ITSP...59...35S. doi:10.1109/TSP.2010.2086452. ISSN 1053-587X. S2CID 15936187.

[4] Stoica, Petre; Li, Jian; Ling, Jun; Cheng, Yubo (April 2009). "Missing data recovery via a nonparametric iterative adaptive approach". 2009 IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE: 3369–3372. doi:10.1109/icassp.2009.4960347. ISBN 978-1-4244-2353-8.

[5] Sward, Johan; Adalbjornsson, Stefan Ingi; Jakobsson, Andreas (March 2017). "A generalization of the sparse iterative covariance-based estimator". 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE: 3954–3958. doi:10.1109/icassp.2017.7952898. ISBN 978-1-5090-4117-6. S2CID 5640068.

[6] Yardibi, Tarik; Li, Jian; Stoica, Petre; Xue, Ming; Baggeroer, Arthur B. (January 2010). "Source Localization and Sensing: A Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares". IEEE Transactions on Aerospace and Electronic Systems. 46 (1): 425–443. Bibcode:2010ITAES..46..425Y. doi:10.1109/TAES.2010.5417172. hdl:1721.1/59588. ISSN 0018-9251. S2CID 18834345.

[7] Panahi, Ashkan; Viberg, Mats (February 2011). "On the resolution of The LASSO-based DOA estimation method". 2011 International ITG Workshop on Smart Antennas. IEEE: 1–5. doi:10.1109/wsa.2011.5741938. ISBN 978-1-61284-075-8. S2CID 7013162.

[Percival1993-8] Percival, Donald B.; Walden, Andrew T. (1992). Spectral Analysis for Physical Applications. Cambridge University Press. ISBN 9780521435413.

[Burg-9] Burg, J.P.(1967) "최대 엔트로피 스펙트럼 분석", 오클라호마주 오클라호마시티 탐사 지구물리학회 제37차 회의 진행.

[10] Hayes, Monson H., Statistical Digital Signal Processing and Modeling, John Wiley & Sons, Inc., 1996.ISBN 0-471-59431-8.

[Lerga-11] Lerga, Jonatan. "Overview of Signal Instantaneous Frequency Estimation Methods" (PDF). University of Rijeka. Retrieved 22 March 2014.

[1]

[2]

[3]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

Search

스펙트럼 밀도 추정

네임스페이스

더

목차

개요

기술

모수 추정

주파수 추정

싱글톤

멀티톤

계산 예시

「」를 참조해 주세요.

레퍼런스

추가 정보

Search

스펙트럼 밀도 추정

개요

기술

모수 추정

주파수 추정

싱글톤

멀티톤

계산 예시

「 」를 참조해 주세요.

레퍼런스

추가 정보

「」를 참조해 주세요.