삼각파 시간 영역(위)과 주파수 영역(아래)에서 촬영되는 대역 제한 삼각파[1] 기본은 220Hz(A3 )입니다. 일반적인 정의 x ( t ) = 4 t − ⌊ t + 3 / 4 ⌋ + 1 / 4 − 1 {\displaystyle x(t)=4\좌회전 t-\lfloor t+3/4\우회전 -1} 적용 분야 전자제품, 신시사이저 도메인 R \displaystyle \mathbb {R} 코도메인 [ − 1 , 1 ] \displaystyle \left[-1,1\right] 패리티 이상한 기간 1 뿌리 { n 2 } , n ∈ Z \displaystyle \left\{\tfrac {n}{2}}\right\},n\in \mathbb {Z} 파생상품 사각파 푸리에 급수 x ( t ) = − 8 π 2 ∑ k = 1 ∞ ( − 1 ) k ( 2 k − 1 ) 2 죄 ( 2 π ( 2 k − 1 ) t ) {{displaystyle x(t)=-{\frac {8}{\pi }^{2}}\sum _{k=1}^{\infty }{\frac {\frac1\right}} ^{k}{\left(2k-1\right)^{2}}\sin \left(2\pi \left(2k-1\right)t\right)}
이 파일을 재생하는 데 문제가 있습니까? 미디어 도움말을 참조 하십시오. 매초마다 사인파에 고조파를 더해 220Hz의 삼각파를 생성한다.
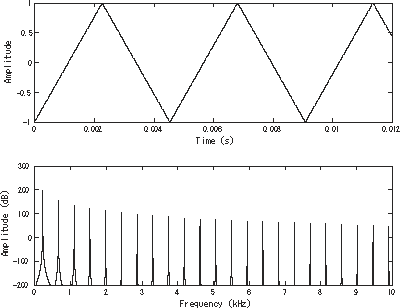
이 파일을 재생하는 데 문제가 있습니까? 미디어 도움말을 참조 하십시오. 삼각형 파형 또는 삼각형 파형은 삼각형 모양에서 이름이 붙여진 비 사인파 파형입니다.이것은 주기적 인, 부분적 인 선형 연속 실함수입니다.
사각파 처럼 삼각파에는 홀수 고조파만 포함되어 있습니다.그러나 높은 고조파 는 사각파보다 훨씬 빠르게 롤오프됩니다 (단순히 역수가 아닌 고조파 숫자의 역제곱에 비례합니다).
정의들 정의. [0,1] 범위에 걸친 주기 p의 삼각형 파형은 다음과 같이 정의됩니다.
x ( t ) = 2 t p − ⌊ t p + 1 2 ⌋ {\displaystyle x(t)=2\left {p}-\left\lfloor {p}+{\frac {1}{2}}\right\floor \right} 여기서 ⌊display displaystyle ） 플로어 기능입니다. 이는 톱니파 이동의 절대값으로 볼 수 있습니다.
[-1,1] 범위에 걸친 삼각파의 경우 식은 다음과 같습니다.
x ( t ) = 2 2 ( t p − ⌊ t p + 1 2 ⌋ ) − 1. {\displaystyle x(t)=2\left 2\frac {t}-\left\lfloor {t \over p}+{1 \over 2)\right \loor \1.}
모듈 로 연산과 절대값 을 사용하여 진폭 displaystyle } 주기 displaystyle }
y ( x ) = 4 a p ( ( x − p 4 ) 모드 p ) − p 2 − a . {\displaystyle y(x)=frac {4a}{p}}\left(\left(x-{\frac {p}{4}}\right)-{\frac {p}{2}}\right - a}
예를 들어, 진폭 5 및 주기 4의 삼각형 파형의 경우:
y ( x ) = 5 ( ( x − 1 ) 모드 4 ) − 2 − 5. {\displaystyle y(x)=5gbigl}\left(x-1){\bmod {4}}\right)-2gbigr}-5. }
위상 편이는 -p 4 (\displaystyle -p/4) 수직 \displaystyle -a}
모듈로 연산과 절대값만을 사용하기 때문에 하드웨어 전자제품에 삼각파를 간단하게 구현할 수 있습니다.
많은 프로그래밍 언어에서는 %연산자는 모듈 로 연산자가 아닌 나머지 연산자(배당과 같은 부호)입니다; 모듈로 연산자 는 다음을 사용하여 얻을 수 있습니다. ((x % p) + p) % p대신해서 x % p예를 들어 JavaScript에서 이것은 형식의 방정식을 낳는다. 4*a/p * Math.abs((((x-p/4)%p)+p)%p - p/2) - a.
사각파와의 관계 삼각파는 사각파 의 적분 으로 표현될 수도 있습니다.
x ( t ) = ∫ 0 t sgn ( 죄 u p ) d u . {\displaystyle x(t)=\int _{0}^{t}\operatorname {sgn}\left(\sin {frac {u}}\right),du}
삼각함수에서의 식 주기 p와 진폭 a를 갖는 삼각형 파형은 사인 및 아크신 (값 범위가 -θ/2 ~ θ /2인 경우)으로 표시할 수 있습니다.
y ( x ) = 2 a π 아크신 ( 죄 ( 2 π p x ) ) . (\displaystyle y(x)=syn frac {2a}{\pi }}\arcsin \left(\sin \left\frac {2\pi }{p}x\right}\right). } 항등 θ = p x textstyle \cos }=\sin \leftfrac {p}{4}}-x\right) 이 위상 편이 삼각형 파형은 코사인 및 아크코신 으로도 표현할 수 있습니다. y ( x ) = a − 2 a π 아크 ( 왜냐하면 ( 2 π p x ) ) . (\displaystyle y(x)=a-{\frac {2a}{\pi }}\arccos \left(\cos \leftfrac {2\pi }{p}x\right}\right). }
교대 선형 함수로 표현됨 -1 ~ 1, 주기 p의 삼각형 파형의 또 다른 정의는 다음과 같습니다.
x ( t ) = 4 p ( t − p 2 ⌊ 2 t p + 1 2 ⌋ ) ( − 1 ) ⌊ 2 t p + 1 2 ⌋ {\displaystyle x(t)=parcfrac {4}{p}\left(t-{\frac {p}{2}}\lfloor {p}+{\frac {1}{right}(-1)^{\lfloor {p}+{fright}{frac}{frc}}{floor {fright}{floor {fright}}}
고조파 고조파 수가 증가하는 삼각파의 가법 합성의 애니메이션. 수학적 설명은 푸리에 분석을 참조 하십시오. 모든 다른 홀수 고조파에 -1을 곱하고(또는 동등하게, 위상변화), 고조파의 진폭에 그들의 모드 번호 근사할 수 있다. 기본 주파수에 대한 상대 주파수)입니다.
위의 내용은 다음과 같이 수학적으로 요약할 수 있습니다.
x t r i a n g l e ( t ) = 8 π 2 ∑ i = 0 N − 1 ( − 1 ) i n − 2 죄 ( 2 π f 0 n t ) {\displaystyle {displaystyle {nt}x_{\mathrm {nt}&{}=sum _ {i=0}^{N-1}(-1)^{i}n^{-2}\sin \left (2\pi f_{0}nt\}\end}}\signed 여기 수이고 , t는 독립 변수(예: 음파의 시간), f ({ displaystyle f_{0 i = 2i 1 displaystyle =2i+ }) 모드 번호
이 무한 푸리에 급수는 애니메이션에서 보듯이 N이 무한대 경향이 있기 때문
호 길이 s 로 표시 된 삼각파의 주기당 호 길이 는 진폭 a 와 주기 길이 p의 관점에서 다음과 같이 주어진다.
s = ( 4 a ) 2 + p 2 . {{displaystyle s=sargrt {(4a)^{2}+p^{2}}}}. }
「 」를 참조해 주세요. 레퍼런스
![{\displaystyle \left[-1,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79566f857ac1fcd0ef0f62226298a4ed15b796ad)
갖는 삼각파에 대한 보다 일반적인 방정식은 다음과 같습니다.
사용하여 삼각형 "코사인" 파형에서 삼각형 "코사인" 파형으로 변환할 수 있습니다.이 위상 편이 삼각형 파형은 
